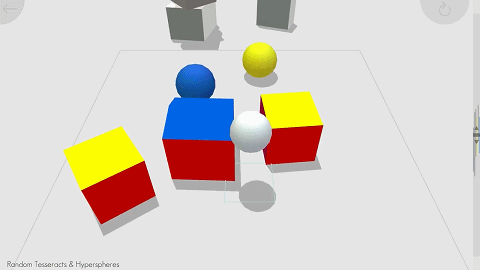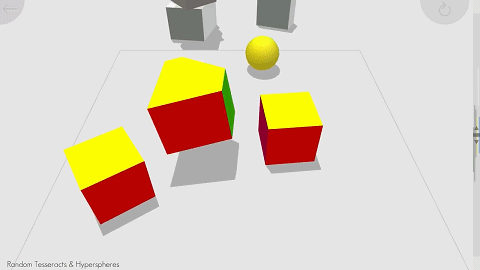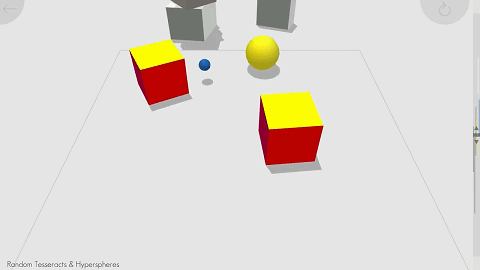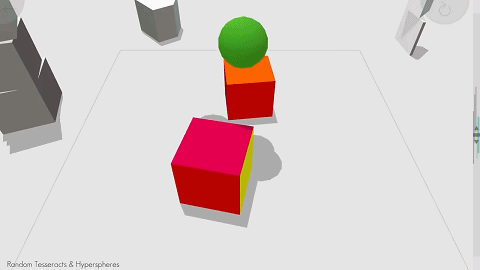
真·降维打击：这篇SIGGRAPH 2020论文帮你「想象」三维生物眼里的四维空间

机器之心报道

参与：张倩、小舟、蛋酱

四维空间是什么样子？里面的物体如何运动？一篇 SIGGRAPH 2020 论文帮我们 “想象” 出了这个过程，看完论文，你还可以上手试试游戏。

四维空间是什么？三个空间维度加一个时间维度？不，那是四维时空，跟四维空间是两个不同的概念。

四维空间的第四个维度也是空间维度，和我们熟知的 x、y、z 属于同一性质。

作为一个三维世界的生物，人类是很难想象出四维空间的，就像一个困在二维空间里的人无法想象三维空间一样。

对于这个二维世界的小人来说，一个三维世界的物体是神秘莫测的，它会时而变换形态，时而消失，因为该物体转换了角度或移动到了第三个维度。所以，对于一个没有 上帝视角的二维世界小人来说，预测三维物体的移动轨迹、形状变化着实有点困难，因为他只能看到一条条变幻莫测的线。

同理，在一个四维空间里，我们就变成了那个可怜的小人，眼前的四维物体似乎和三维物体没什么两样，但当它们在四维空间自由移动、碰撞时，我们也会发现它们时而变换形态，时而消失不见。

这种情景我们通常只会想象一下，毕竟在现实生活中是体验不到的。但也有人对此兴味盎然，将其搬到了游戏世界中，甚至还凭借游戏的论文中了计算机图形学顶会 SIGGRAPH。

在这篇论文中，研究者提出了一个适用于任何空间维度的刚体动力学公式。用几何代数来描述刚体的状态和运动方程。他将碰撞检测算法扩展到𝑛维，解析了物体之间的碰撞和接触。虽然作者实现的是四维，但该方法可以扩展到任意维度。他通过这些四维刚体的三维截面来展示他们，用户可以实时操纵这些物体。

不同于常见的研究，这篇 6 页的论文充满了各式各样的几何代数公式。在双盲审稿过程中，一位审稿人对该论文的评价是：「异想天开（whimsical）」。

大部分研究工作都是从 2012 年开始的，但作者也根据审稿人的建议增加了关于神秘翻转（Dzhanibekov effect）的部分。

在此之前，物理模拟一直集中并局限于二维和三维的情况。但作者提出，使用所需方程式的恰当公式，就有可能将它们推广到更高维度。几何代数提供了一个简单的与维度无关的公式，可以实时操作相互碰撞的 n 维物体，就好像它们是真实的物体一样。这使得这些高维物体不那么抽象，和大多数人对它们的体验形成鲜明对比。

这篇论文的贡献在于：

1、将基于几何代数的经典三维刚体动力学公式推广到了 n 维。通过将几何代数算子表示为矩阵，以一种简单的方式构建、对角化（diagonalize）、转换任意 n 维简单网格，无论这个 n 是多少。这样一来，就可以在 n 维中建立欧拉方程，比如研究四维欧拉方程在无力矩条件下的情况。

2、计算 n 维中的碰撞和接触处理过程，包括静摩擦和动摩擦。作者给出了 Minkowski 差分法和基于几何代数的分离轴定理碰撞检测方法的 n 维公式。

3、提出了一种类似于我们对现实三维空间体验的四维物体互动方法。

也许这篇论文最大的意义在于，它为我们提供了一种从侧面了解四维空间的方式。

基于这篇论文中提到的技术，论文作者 Marc ten Bosch 开发了两款游戏，上面动图展示的就是其中一款游戏——「4D Toys」。这款游戏旨在以三维视角展示四维物体在四维空间里的特性。有人表示，该游戏就像在向一位盲人解释颜色的含义。目前，该游戏已经在 Steam、IOS 等平台上线。

除此之外，他还打造了另外一款 4D 游戏「Miegakure」。在这个游戏中，一系列平行的 3D 世界因谜题而串联在一起，玩家可用视角转换的方式触发穿越机制，到达其他的 3D 场景。

在 SIGGRAPH 2020 技术论文专场，作者也将详细介绍 4D Toys 和 Miegakure 游戏。 对于 Miegakure  的老粉来说，论文被大会接收也令他们 激动不已：

还有人表示：「终于等到点书面的资料了，感觉 follow 这项研究已经有十年了！」

估计这也是 SIGGRAPH 2020 技术论文计划开展以来，史上第一项介绍独立游戏的研究吧。

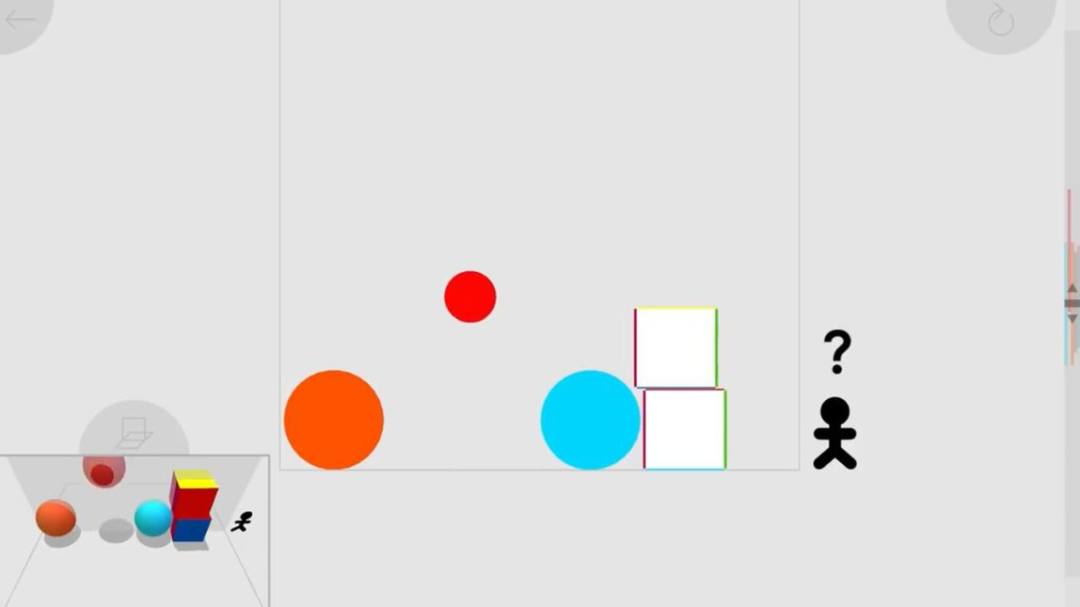
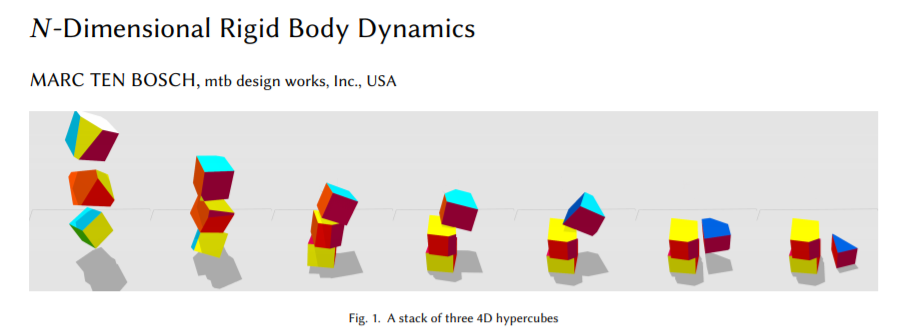
• 论文地址：https://marctenbosch.com/ndphysics/NDrigidbody.pdf

• 论文介绍界面：https://marctenbosch.com/news/2020/05/siggraph-2020-technical-paper-n-dimensional-rigid-body-dynamics/

5 月 12 日，机器之心联合华为昇腾学院开设的线上公开课《轻松上手开源框架 MindSpore》第六课将正式开讲，主题为「MindSpore可视化工具使用指南」，欢迎读者报名学习。