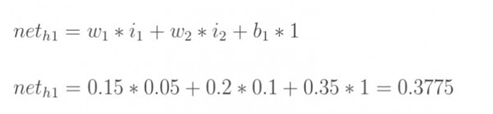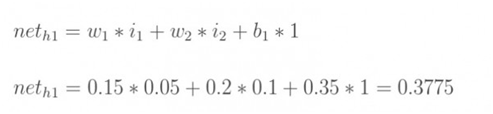深度学习,其实和撩妹的套路一样!
如果在这个人工智能的时代,作为一个有理想抱负的程序员,或者学生、爱好者,不懂深度学习这个超热的话题,似乎已经跟时代脱节了。
但是,深度学习对数学的要求,包括微积分、线性代数和概率论与数理统计等,让大部分的有理想抱负青年踟蹰前行。那么问题来了,理解深度学习,到底需不需要这些知识?
关于深度学习,网上的资料很多,不过大部分都不太适合初学者。主要有以下两个原因:
深度学习确实需要一定的数学基础。如果不用深入浅出地方法讲,有些读者就会有畏难的情绪,因而容易过早地放弃。
中国人或美国人写的书籍或文章,普遍比较难。
但是深度学习所需要的数学基础并没有想象中的那么难,只需要知道导数和相关的函数概念即可。假如你高等数学也没学过,很好,这篇文章其实是想让文科生也能看懂,只需要学过初中数学。
“王小二卖猪”解读深度学习之导数
导数是什么?
无非就是变化率,比如:王小二今年卖了 100 头猪,去年卖了 90 头,前年卖了 80 头。。。变化率或者增长率是什么?每年增长 10 头猪,多简单。
这里需要注意有个时间变量—年。王小二卖猪的增长率是 10头/年,也就是说,导数是 10。
函数 y = f(x) = 10x + 30,这里我们假设王小二第一年卖了 30 头,以后每年增长 10 头,x代表时间(年),y代表猪的头数。
当然,这是增长率固定的情形,而现实生活中,很多时候,变化量也不是固定的,也就是说增长率不是恒定的。
比如,函数可能是这样: y = f(x) = 5x² + 30,这里 x 和 y 依然代表的是时间和头数,不过增长率变了,怎么算这个增长率,我们回头再讲。或者你干脆记住几个求导的公式也可以。
深度学习还有一个重要的数学概念:偏导数
偏导数的偏怎么理解?偏头疼的偏,还是我不让你导,你偏要导?
都不是,我们还以王小二卖猪为例,刚才我们讲到,x 变量是时间(年),可是卖出去的猪,不光跟时间有关啊,随着业务的增长,王小二不仅扩大了养猪场,还雇了很多员工一起养猪。
所以方程式又变了:y = f(x) = 5x₁² + 8x₂ + 35x₃ + 30
这里 x₂ 代表面积,x₃ 代表员工数,当然 x₁ 还是时间。
以撩妹为例,解读深度学习之“偏导数”
偏导数是什么
偏导数无非就是多个变量的时候,针对某个变量的变化率。在上面的公式里,如果针对 x₃ 求偏导数,也就是说,员工对于猪的增长率贡献有多大。
或者说,随着(每个)员工的增长,猪增加了多少,这里等于 35—每增加一个员工,就多卖出去 35 头猪。
计算偏导数的时候,其他变量都可以看成常量,这点很重要,常量的变化率为 0,所以导数为 0,所以就剩对 35x₃ 求导数,等于 35。对于 x₂ 求偏导,也是类似的。
求偏导,我们用一个符号表示:比如 y / x₃ 就表示 y 对 x₃ 求偏导。
废话半天,这些跟深度学习到底有啥关系?当然有关系,深度学习是采用神经网络,用于解决线性不可分的问题。
这里我主要讲讲数学与深度学习的关系。先给大家看几张图:
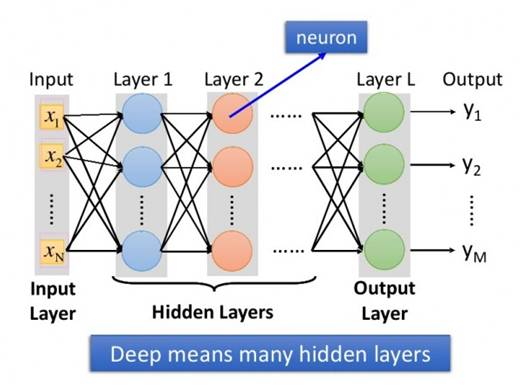
图1:所谓深度学习,就是具有很多个隐层的神经网络
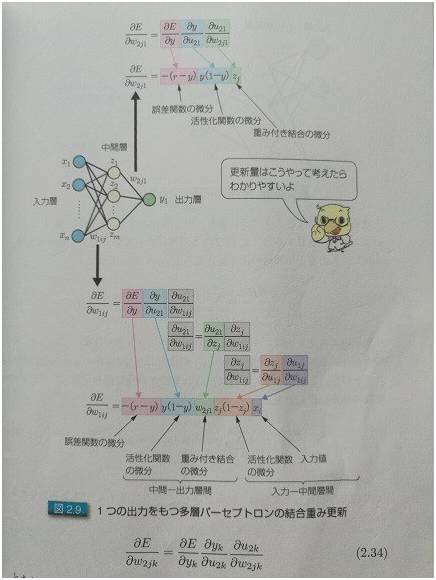
图2:单输出的时候,怎么求偏导数
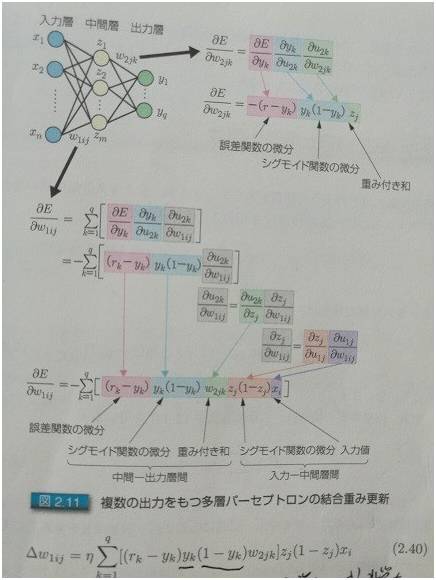
图3:多输出的时候,怎么求偏导数
后面两张图是日本人写的关于深度学习的书里面的两张图片。所谓入力层,出力层,中间层,分别对应于中文的:输入层,输出层,和隐层。
大家不要被这几张图吓着,其实很简单,就以撩妹为例。男女恋爱我们大致可以分为三个阶段:
初恋期。相当于深度学习的输入层。别人吸引你,肯定是有很多因素,比如:身高,身材,脸蛋,学历,性格等等,这些都是输入层的参数,对每个人来说权重可能都不一样。
热恋期。我们就让它对应隐层吧!这个期间,双方各种磨合,柴米油盐酱醋茶。
稳定期。对应输出层,是否合适,就看磨合得咋样了。大家都知道,磨合很重要,怎么磨合呢?就是不断学习训练和修正的过程!
比如女朋友喜欢草莓蛋糕,你买了蓝莓的,她的反馈是 negative,你下次就别买了蓝莓,改草莓了。
看完这个,有些小伙可能要开始对自己女友调参了。有点不放心,所以补充一下。撩妹和深度学习一样,既要防止欠拟合,也要防止过拟合。
所谓欠拟合,对深度学习而言,就是训练得不够,数据不足,就好比,你撩妹经验不足。要做到拟合,送花当然是最基本的,还需要提高其他方面,比如,提高自身说话的幽默感等。这里需要提一点,欠拟合固然不好,但过拟合就更不合适了。
过拟合跟欠拟合相反,一方面,如果过拟合,她会觉得你有陈冠希老师的潜质,更重要的是,每个人情况不一样,就像深度学习一样,训练集效果很好,但测试集不行!
就撩妹而言,她会觉得你受前任(训练集)影响很大,这是大忌!如果给她这个印象,你以后有的烦了,切记切记!
深度学习也是一个不断磨合的过程,刚开始定义一个标准参数(这些是经验值,就好比情人节和生日必须送花一样),然后不断地修正,得出图 1 每个节点间的权重。
为什么要这样磨合?试想一下,我们假设深度学习是一个小孩,我们怎么教他看图识字?
肯定得先把图片给他看,并且告诉他正确的答案,需要很多图片,不断地教他,训练他,这个训练的过程,其实就类似于求解神经网络权重的过程。以后测试的时候,你只要给他图片,他就知道图里面有什么了。
所以训练集,其实就是给小孩看带有正确答案的图片,对于深度学习而言,训练集就是用来求解神经网络的权重,最后形成模型;而测试集,就是用来验证模型的准确度。
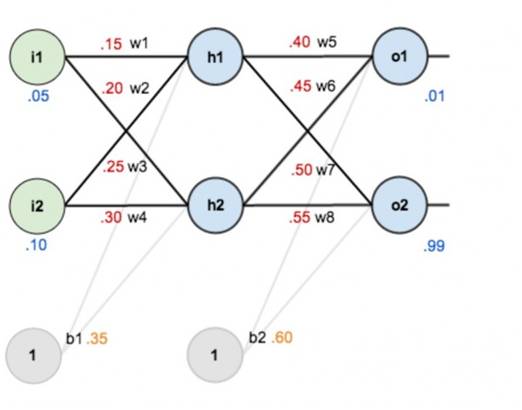
对于已经训练好的模型,如下图所示,权重(w1,w2…)都已知。
像上面这样,从左至右容易算出来。但反过来,测试集有图片,也有预期的正确答案,要反过来求 w1,w2……,怎么办?
怎么求偏导数?
绕了半天,终于该求偏导出场了。目前的情况是:
我们假定一个神经网络已经定义好,比如有多少层,每层有多少个节点,也有默认的权重和激活函数等。输入(图像)确定的情况下,只有调整参数才能改变输出的值。怎么调整,怎么磨合?
每个参数都有一个默认值,我们就对每个参数加上一定的数值∆,然后看看结果如何?如果参数调大,差距也变大,那就得减小∆,因为我们的目标是要让差距变小;反之亦然。
所以为了把参数调整到最佳,我们需要了解误差对每个参数的变化率,这不就是求误差对于该参数的偏导数吗?
这里有两个点:一个是激活函数,主要是为了让整个网络具有非线性特征。我们前面也提到了,很多情况下,线性函数没办法对输入进行适当的分类(很多情况下识别主要是做分类)。
那么就要让网络学出来一个非线性函数,这里就需要激活函数,因为它本身就是非线性的,所以让整个网络也具有了非线性特征。
另外,激活函数也让每个节点的输出值在一个可控的范围内,计算也方便。
貌似这样解释还是很不通俗,其实还可以用撩妹来打比方:女生都不喜欢白开水一样的日子,因为这是线性的,生活中当然需要一些浪漫情怀了,这个激活函数嘛,我感觉类似于生活中的小浪漫,小惊喜。
相处的每个阶段,需要时不时激活一下,制造点小浪漫,小惊喜。比如,一般女生见了可爱的小杯子,瓷器之类都迈不开步子,那就在她生日的时候送一个特别样式,让她感动得想哭。
前面讲到男人要幽默,这是为了让她笑,适当的时候还要让她激动得哭。一哭一笑,多整几个回合,她就离不开你了。因为你的非线性特征太强了。
当然,过犹不及,小惊喜也不是越多越好,但完全没有就成白开水了。就好比每个 layer 都可以加激活函数,当然,不见得每层都要加激活函数,但完全没有,那是不行的。
关键是怎么求偏导。图 2 和图 3 分别给了推导的方法,其实很简单,从右至左挨个求偏导就可以。相邻层的求偏导很简单,因为是线性的,所以偏导数其实就是参数本身嘛,就跟求解 x₃ 的偏导类似。然后把各个偏导相乘就可以了。
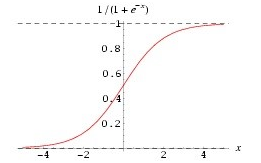
这里有两个点:一个是激活函数,其实激活函数也没啥,就是为了让每个节点的输出都在 0 到 1 的区间,这样好算账,所以在结果上面再做了一层映射,都是一对一的。
由于激活函数的存在,在求偏导的时候,也要把它算进去,激活函数,一般用 sigmoid,也可以用 Relu 等。激活函数的求导其实也非常简单:
求导: f'(x)=f(x)*[1-f(x)]
这个方面,有时间可以翻看一下高数,如果没时间,直接记住就行了。至于 Relu,那就更简单了,就是 f(x) 当 x<0 的时候 y 等于 0,其他时候,y 等于 x。
当然,你也可以定义你自己的 Relu 函数,比如 x 大于等于 0 的时候,y 等于 0.01x,也可以。
什么是学习系数?
另一个是学习系数,为什么叫学习系数?
刚才我们上面讲到∆增量,到底每次增加多少合适?是不是等同于偏导数(变化率)?
经验告诉我们,需要乘以一个百分比,这个就是学习系数,而且,随着训练的深入,这个系数是可以变的。
当然,还有一些很重要的基本知识,比如 SGD(随机梯度下降),mini batch 和 epoch(用于训练集的选择)。
上面描述的内容,主要是关于怎么调整参数,属于初级阶段。上面也提到,在调参之前,都有默认的网络模型和参数,如何定义最初始的模型和参数?就需要进一步深入了解。
课程分隔线
且新增毕业考试且1v1批改,辅助简历优化;全程提供GPU云实验平台、CPU云实验平台,助力跳槽涨薪!扫描下方二维码或点击文末“阅读原文”听课。