一文梳理ICML 2022中图机器学习热点和趋势

©作者 | Mikhail Galkin，Zhaocheng Zhu

译者 | Zhaocheng Zhu

单位 | Mila研究所/麦吉尔大学/蒙特利尔大学

研究方向 | 图机器学习，知识图谱

每年 ICML 都汇集了全球顶级 AI 研究者们的不少工作。在刚过去的 ICML 2022 中，我们看到了上百篇图机器学习相关的工作，以及不少相关的 Workshop [1] 。在此，我们和大家来分享一下当下图机器学习中的研究热点。

我们尽力在这篇文章中涵盖 ICML 中图机器学习的所有方向，每篇方向介绍 2-4 篇论文。由于 ICML 的论文数量庞大，这篇文章难免会遗漏了一些工作。欢迎在文末评论指出。

图生成

今年，Denoising diffusion probabilistic model（DDPM [2] ）以其超越 GAN 和 VAE 的生成质量和理论性质，席卷了深度学习的诸多领域，例如：图像生成（GLIDE [3] ， DALL-E 2 [4] ，Imagen [5] ），视频生成 [6] ，文本生成（Diffusion-LM [7] ），甚至是在 RL 中使用 diffusion [8] 。简单来说，diffusion model 对输入逐步增加噪声（直到它完全变成高斯白噪声），然后学习预测每一步增加的噪声，从而反向消除这些噪声，从噪声中生成输入。

在图机器学习中，diffusion 可能是今年最热的方向——尤其是在药物发现，conformation generation，量子化学等领域中。diffusion 通常会和最新的 equivariant GNN 结合使用。今年 ICML 里我们看到了许多有意思的基于 denoising diffusion 的图生成工作。

Hoogeboom 等人在 Equivariant Diffusion for Molecule Generation in 3D [9] 中 定义了一种 equivariant diffusion model（EDM）用于解决 conformation generation。EDM 对三维欧式空间变换（即旋转，平移和翻转）具有 equivariance，以及对输入点 feature 上的群运算具有 invariance。值得注意的是，分子的 feature 具有很多不同的 modality：比如电荷数是个整数标量，原子类型是个 one-hot feature，分子坐标则是实数向量。因此在分子上用 diffusion 模型的难点在于，你没法通过对所有 feature 暴力加相同的高斯噪声使得模型 work。对此，这篇论文设计了一种针对不同 feature 的加噪方法和 loss，并且调整输入 feature 的尺度来使训练更加稳定。

EDM 用 SotA 的 E(n) GNN [10]  来根据输入 feature 和时间步预测增加的噪声强度。在测试的时候，我们先采样一个原子数 M，然后基于给定的性质 c，让 EDM 来生成分子（由 feature x 和 h 控制）：

EDM 在 negative log-likelihood，molecule stability，uniqueness 等指标上都大幅超过基于 normalizing flow 和基于 VAE 的生成方法。Ablation study 证明了 equivariant GNN 对性能非常重要，无法被普通的 MPNN 取代。EDM 的代码已经在 GitHub 上开源 [11]，值得一试！

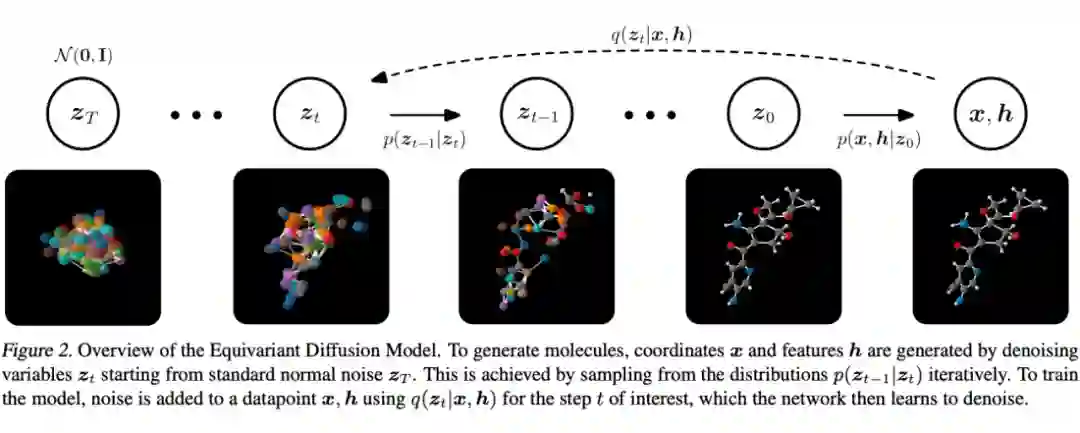
▲ Diffusion 的正向和反向过程。来源：Hoogeboom 等人的工作 [12]

▲ Diffusion动态过程演示。来源：Twitter [13]

Jo，Lee 和 Hwang 提出了解决二维图生成的 Graph Diffusion via the System of Stochastic Differential Equations（GDSS）[14]。前面提到的 EDM 是一种 denoising diffusion probabilistic model（DDPM），GDSS 则属于 DDPM 的一个近亲，score-based model。前不久 ICLR’21 的工作 [15] 得出一个结论，如果我们把正向的 diffusion 过程用随机微分方程（SDE）解释的话，DDPM 和 score-based model 是可以统一为一个框架的。

SDE 允许模型在连续空间里像 Wiener process [16] （可以理解为一种花式加噪声的方式）那样进行 diffusion，而 DDPM 通常需要离散化成 1000 步加噪过程和时间步的 embedding。

当然，SDE 需要依赖一些复杂的求解器进行计算。跟先前 score-based 图生成方法比，GDSS 取邻接矩阵  和点 feature 作为输入，并同时预测这两。SDE 中的正向和反向 diffusion 需要计算 score，也就是  和  联合概率的对数的梯度。为了预测这个联合概率，我们需要一个score-based model。论文里作者们用的是一个带 attention pooling 的 GNN [17] 。

训练过程需要解一个 forward SDE，并且训一个 score model。测试时，我们用训好的 score model 来求解 reverse-time SDE。通常这需要涉及到 Langevin dynamics [18] ，例如 Langevin MCMC，不过理论上也可以用高阶的 Runge-Kutta [19] 求解器。GDSS 在二维图生成任务中大幅超过 autoregressive 生成模型和 one-shot VAE，尽管由于 reverse-time SDE 的存在，采样速度不尽人意。GDSS 的代码 [20] 已经开源了！

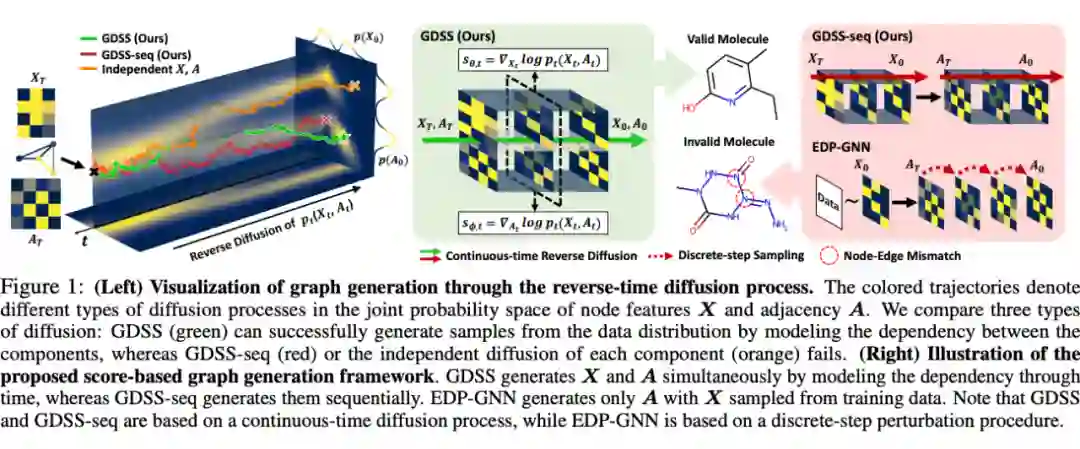
▲ GDSS模型。来源：Jo，Lee和Hwang的工作 [14]

根据最近 arXiv 的情况来看，估计今年还会有不少 diffusion model 出来——DDPM 在图上的应用值得我们单独开一篇博客来写。大家可以期待一下！

最后我们来介绍一篇非 diffusion 的生成工作。Martinkus 等人 [21] 提出了SPECTRE [22] ，一种解决 one-shot graph generation 的 GAN 模型。跟其他直接生成邻接矩阵的 GAN 不同的是，SPECTRE 根据 Laplacian 的最小的 k 个特征值和特征量来生成图。这意味着我们可以显示控制图的连通性和聚类属性。

生成的过程一共有三步：1）SPECTRE 先生成 k 个特征值；2）在最小 k 个特征向量导出的 Stiefel manifold [23] 上采样得到 k 个特征向量。Stiefel manifold 涵盖了各种标准正交阵，我们可以从中采单个  的矩阵；3）最后，论文用 Provably Powerful Graph Net [24] 把特征值和特征向量转化为邻接矩阵。

SPECTRE 在实验上比其他 GAN 方法有极大的提升，并且比 autoregressive 的图生成方法快了近 30 倍。

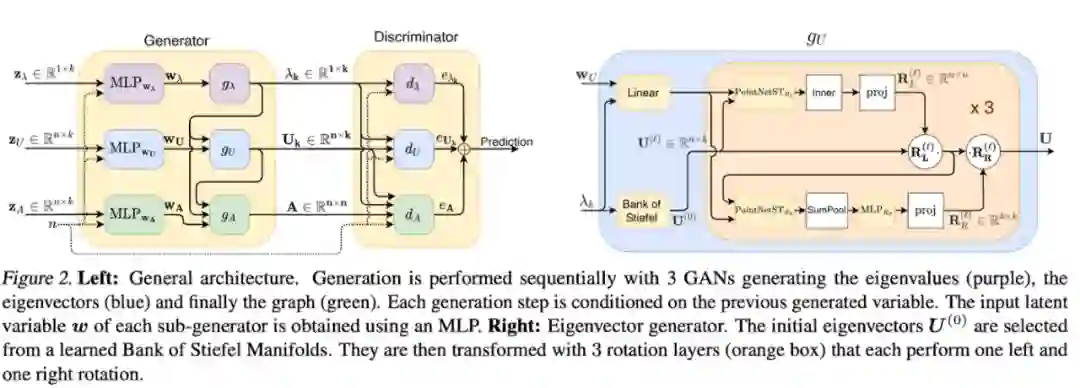
▲ SPECTRE的三步生成过程：特征值→特征向量→邻接矩阵。来源：Martinkus等人 [21]

图Transformer

今年 ICML 有两篇工作改进了图 Transformer。

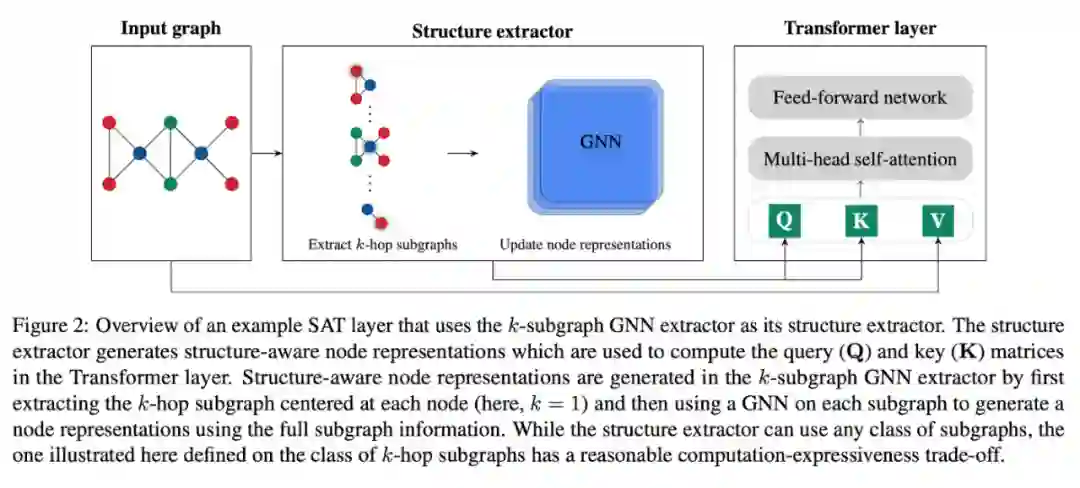
第一篇论文是 Chen 等人 [25] 提出的 Structure-Aware Transformer（SAT）。他们注意到 self-attention可以看作一种用 exponential kernel 作为query-key product 的 kernel smoothing。从这个角度，我们可以探讨如何设计一种更 general 的 kernel。

这篇论文提出用点和图上的函数，k-subtree 和 k-subgraph 来增加 Transformer 对结构信息的表达能力。k-subtree 即点的 k-hop 邻域，可以被非常快速地提取出来，但表达能力无法超过 1-WL test。而 k-subgraph 的计算代价则更大，但是能提供更强的表达能力。

无论你使用哪种 feature 方式，我们都可以用一个 GNN（例如 PNA）来 encode每个点的 subtree 或 subgraph，通过图层面的 pooling（sum / mean / 虚拟点）得到一个 feature，用在 Transformer 的 self-attention 里作为 query 和 key（见下图）。

实验表明，在 k-subtree 和 k-subgraph 中，k 取 3 或者 4 即可。当我们能接受 k-subgraph 的计算时间时，k-subgraph 得到的结果要明显好于 k-subtree。一个有趣的现象是，诸如 Laplacian 的特征向量和随机游走 feature 等 positional feature 只对 k-subtree SAT 有用，对 k-subgraph SAT 并无太大帮助。

▲ 来源：Chen等人 [25]

第二篇论文是 Choromanski，Lin，Chen 等人 [26]（和著名的线性 attention 论文 Performer [27] 几乎是同一拨人）研究 sub-quadratic 复杂度的 attention 的工作。具体来说，他们考虑了图像、音频、视频和图等不同  modality 下 relative positional encoding（RPE）及其变种。

就图而言，我们知道在 attention 中使用最短路距离的 Graphformer 很好用，但它的计算需要实例化整个 attention 矩阵（也就不 scalable）。我们能否设计一种不需要实例化整个矩阵，同时又能整合图 inductive bias 的 softmax attention 方式呢？

答案是肯定的！这篇论文就提出了两种机制：1）我们可以用 Graph Diffusion Kernel（GDK）。GDK 又叫作 heat kernel，可以用于模拟热传播的过程，在这里我们可以把它看作一种 soft 的最短路。然而  Diffusion 需要通过特殊的求解器来计算矩阵的幂，所以这篇论文设计了另一种方案；2）Random Walks Graph-Nodes Kernel（RWGNK）用于计算两个点各自随机游走产生的频率向量的点乘。

没错，随机游走就是这么有效！大家可以在下方图里看到 diffusion 和随机游走 kernel 的结果。论文最终用的基于 RWGNK 的 transformer 叫作 Graph Kernel Attention Transformer（GKAT），并在一众合成数据集、计算生物数据集和社交网络数据集上进行了测试。GKAT 在合成任务上取得了更好的结果，在其他图任务上跟普通 GNN 齐平。可以说，有了这篇工作，Transformer 的 scalability 几乎只受制于输入本身的大小了！

▲ 来源：Choromanski，Lin，Chen等人 [26]

GNN理论和表达能力

整个 GNN 领域一直在努力寻找突破 1-WL test 同时保持较低的多项式复杂度的GNN 设计。

Papp 和 Wattenhofer [28] 对理论领域现状提出了一个精准的总结：

每当一个新的 GNN 变种出现时，大家总会用理论去论证这个模型比 1-WL test 强，有时候还会跟经典的 k-WL 分类系统进行比较…… 我们能否设计一个更有意义的衡量 GNN 表达能力的方式？

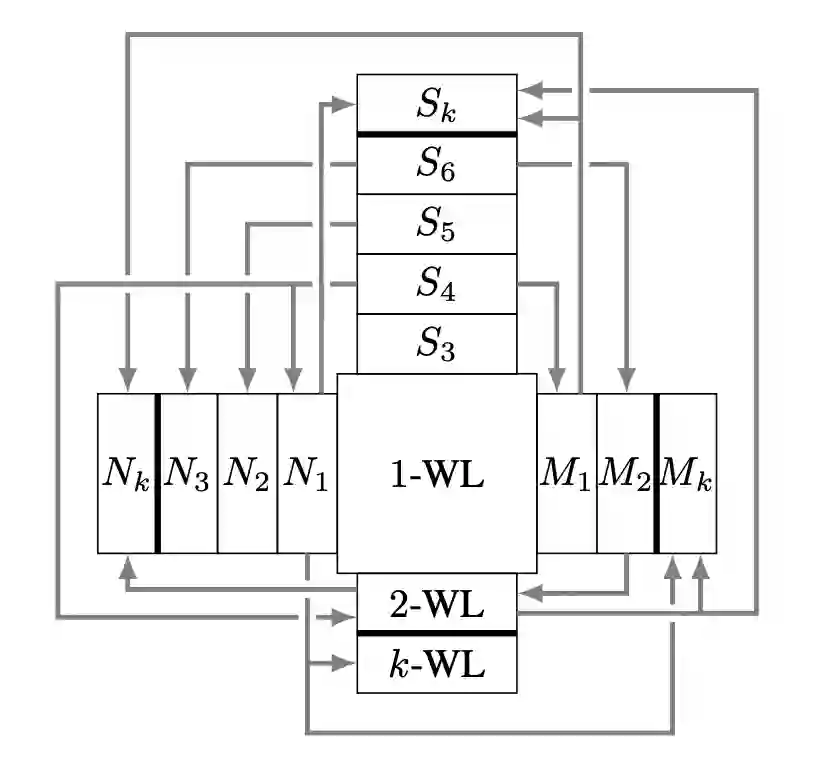
这篇论文将 GNN 表达能力的相关工作分为了 4 个大类：1）k-WL 家族及其近似；2）子结构计数（S 类）；3） 提取子图和邻域的 GNN（N 类）（Michael Bronstein 最近的一篇博客详细探讨过这类 [39] ）；4）带标记的 GNN，例如在点或者边上进行扰动或者打标记的（M 类）。论文在理论框架下讨论了 k-WL，S，N 和 M 四类的关系，以及哪个比哪个强，强多少。这套分类系统比 k-WL 更加精细，有助于设计恰好覆盖任务需求同时节省计算成本的 GNN。

▲ GNN表达能力的分类系统。N表示子图GNN，S表示子结构计数，M表示带标记的GNN。来源：Papp和Wattenhofer [28]

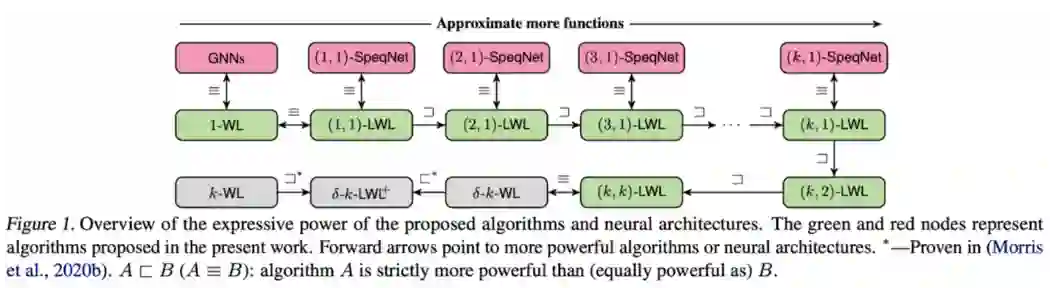
今年 ICMl 最“香”的论文估计是 Morris 等人 [28] 的 SpeqNet 了（注：Speq 在德语里是培根 speck 的谐音）。我们知道高阶的 k-WL GNN 要么依赖 k 维tensor，要么需要考虑所有 k 个点组成的子图，都是关于 k 指数增长的复杂度，没法充分利用图的稀疏性。SpeqNet 提出了一种新的图同构问题的启发算法 (k,s)-WL，可以更精细地控制表达能力和速度的取舍。

论文探讨了一种只需要考虑部分点集的局部 k-WL test，避免了 k-WL 那样指数的时间复杂度。具体来说，论文中只考虑不超过 s 个连通分量的 k 元组或 k 个点组成的子图，有效地利用了图的稀疏特性。通过调整 k 和 s 的取值，我们可以从理论上控制模型的速度和表达能力。

基于上述思想，论文提出了一类新的 permutation-equivariant 的 GNN，SpeqNet。和高阶 GNN 相比，SpeqNet 在点和图任务的监督学习上大幅降低了计算时间。相较于标准 GNN 和图 kernel 而言，SpeqNet 显著提高了预测性能。

▲ SpeqNet模型。来源：Morris等人 [28]

下一篇论文是 Huang 等人 [30] 的一个神奇发现：精挑细选的 permutation-sensitive GNN 能比常规的 permutation-invariant GNN 具有更强的表达能力。在此之前，Janossy pooling [31] 曾提出，任何一个 permutation-sensitive 的模型，只要在训练中见过输入数据的所有 permutation 变换，就能达到 permutation-invariant 的效果。

Janossy pooling 的问题是  个元素的 permutation 变换，本身就高达  种，复杂度无法接受。这篇论文提出，即便是只考虑一个点邻域中每个点对的 permutation，模型的表达能力也强于 2-WL test，甚至不差于 3-WL test。

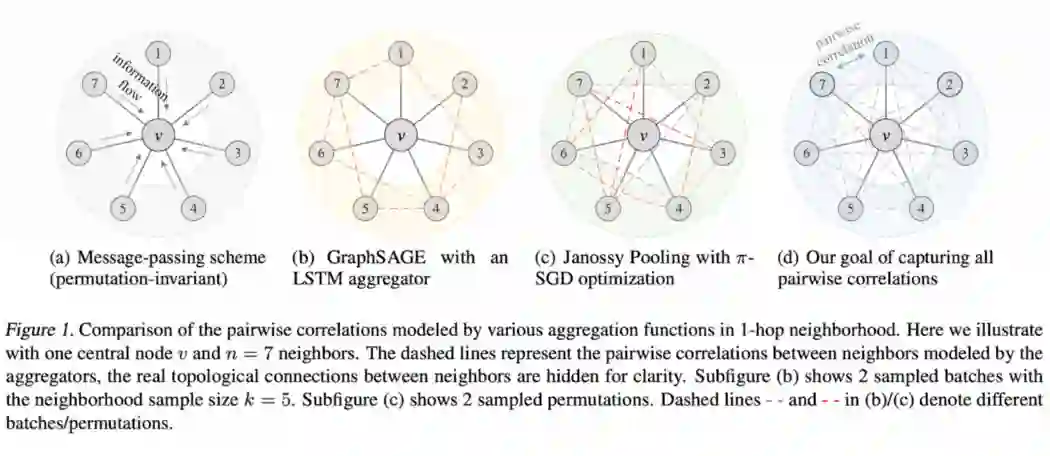
从实现上来说，论文提出的 PG-GNN [32] 可以看作 GraphSAGE 的一种扩展。PG-GNN 用一个双层的 LSTM 来聚合一个点邻域，而不是像常规 GNN 中使用 sum/mean/min/max 来聚合。此外，论文还基于 Hamilton 回路设计了一种线性的 permutation 采样算法。

▲ PG-GNN中permutation-sensitive的聚合方式。来源：Huang等人 [30]

其他有趣的理论文章还有：

Cai 和 Wang [33] 研究了 Invariant Graph Networks [34]（IGN）的收敛性质。跟一般 MPNN 不同的是，IGN 把点和边的 feature 当作一个完整的 tensor 进行操作。基于 graphon [35] 理论，论文发现某一类 IGN 的收敛性是有理论保证的。作者们发了一个很棒的 Twitter [36] 来介绍这个工作！

Gao 和 Riberio [37] 研究了两类时序 GNN：1）时序与图——先用 GNN embed 每个时间点上的图，再用 RNN 处理时序；2）先时序后图——在一个叠加所有时间点的图上，先用 RNN encode 所有点和边的 feature，再用 GNN 处理一遍。典型的方法有 TGN [38] 和 TGAT [39]。

论文从理论上证明了当我们用 1-WL GNN（例如 GCN 或者 GIN）时，先时序后图的表达能力更强。基于此，论文提出了一个简单的 GRU+GCN 的模型。这个模型在时序点分类和回归任务上，能取得跟已有模型相近的结果，同时节约显存以及快 3-10 倍不等。有趣的是，论文指出无论是时序与图，还是先时序后图，它们的表达能力对于时序边预测任务都是不够的。

最后一篇论文是来自 Chen，Lim，Mémoli，Wan 和 Wang 等人 [40]（五位共一）的 Weisfeiler-Lehman Meets Gromov-Wasserstein。他们从 WL kernel出发，推出了一种多项式复杂度的 WL 距离 [41]，可以用于衡量两个图的差异大小。WL 距离为 0 当且仅当两张图无法被 WL test 区分，非 0 当且仅当它们可以被 WL test 区分。论文还指出 WL 距离和 Gromov-Wasserstein 距离 [42] 有很强的联系！

▲ 当Weisfeiler-Leman遇上Gromov-Wasserstein。Chen，Lim，Mémoli，Wan和Wang等人 [40] 应该用这个图的。来源：Tenor [43]

谱GNN

我们估计大多数人只关注 GNN 堆模型的手法，很少有人留意谱 GNN，不过下面这篇论文可能会让你有入坑谱 GNN 的想法。在 Wang 和 Zhang [44] 提出的 How Powerful are Spectral Graph Neural Networks 中，他们发现，只需一些简单的假设，就可以证明线性谱 GNN 是一个图上任意函数的 universal approximator。更有意思的是，这些简单的假设在主流的数据集上都成立。换言之，一个线性的谱 GNN 的表单能力，对于半监督点分类任务而言已经足够了！

但不同的谱 GNN 在实验中还是有性能上的区别的，这又如何解释呢？论文证明了选择不同的 parameterization（各种多项式基函数），会对谱 GNN 的收敛速度产生影响。我们知道 Hessian 矩阵的 condition number（相当于 loss 面上等高线有多圆）能直接决定 SGD 的收敛速度。

基于这个思路，论文提出用正交的多项式基函数来帮助优化。论文中使用的 Jacobi 基函数 [45] ，是 ChebyNet [46] 中使用的 Chebyshev 基函数 [47] 的一种更广义形式。Jacobi 基函数由  和  两个超参数决定。我们可以通过调整这两超参，找到一组有助于拟合输入图信号的基函数。

虽然是个线性谱模型，JacobiConv 在 homophilic 数据集和 heterophilic 数据集上都取得了很好的效果。至少在点分类任务上，我们可以抛弃那些过于复杂、华而不实的模型了。

今年还有两篇跟谱 GNN 相关的论文。一篇是根据谱 concentration analysis 推出的 Graph Gaussian Convolutional Networks [48] （G2CN），在 heterophilic 数据集取得了不错的效果。另外一篇是 Yang 等人 [49] 根据谱平滑程度分析图卷积中相关性问题的论文。他们的模型在 ZINC 数据集上取得了 0.0698 的 MAE，非常厉害。

可解释的GNN

由于绝大多数 GNN 模型都是个黑箱，研究可解释的 GNN 对于 GNN 的应用来说有着很大的意义。今年 ICML我们有两篇这样的文章，一篇是 Xiong 等人 [50] 提出的一种高效且强大的 post-hoc 解释算法，一篇则是 Miao 等人 [51] 的直接可解释模型。

Xiong 等人 [50] 对他们之前一篇可解释的 GNN 工作 GNN-LRP [52] 的效率进行了大幅改进。跟之前 post-hoc 解释算法（GNNExplainer [53] ，PGExplainer [54] ，PGM-Explainer [55] ）不同的是，GNN-LRP 是一种高阶的子图贡献算法。

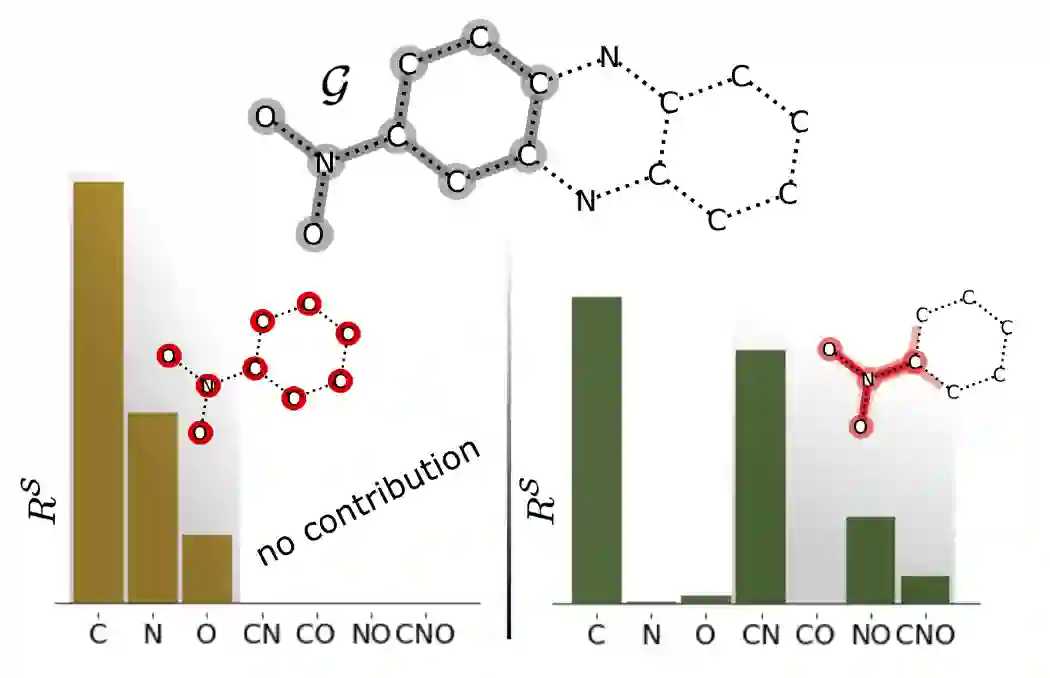
GNN-LRP 考虑一个子图中所有点的联合贡献，而不是点的独立贡献的总和。这对于依赖子图联合语义的任务有很大的价值。比如说在分子中，6 个碳原子组成的子图（一般不考虑氢原子），可以是一个苯环（环结构），也可以是个己烷（链结构）。仅考虑点的独立贡献无法区分这两子图的语义。下图中展示了高阶贡献算法（右）和低阶贡献算法（左）的这种效果差别。

▲ 低阶贡献（左）与高阶贡献（右）。来源：Xiong等人[50]

当然，高阶总是有代价的。GNN-LRP 需要考虑子图中所有可能的随机游走，对于一个子图 S 和 L-hop 的随机游走来说，其时间复杂度是  。解决办法当然是用动态规划了。我们注意到模型预测对于一个随机游走的导数是乘法关系（链式法则），而对不同随机游走之间的导数是加法关系。于是我们可以用 sum-product 算法来高效地求解这个问题。

本质上来说，这利用的是乘法对加法的分配律（离散数学里把这样的两个运算符叫作半环 [56] ）。原本枚举所有路径的问题，就变成了每步中枚举一步转移的问题。由此，我们得到了多项式复杂度的 subgraph GNN-LRP [57] （sGNN-LRP）。

sGNN-LRP 中还定义了一种广义的子图贡献，除了考虑子图 S 中的随机游走外，还考虑其补图，也就是 G\S 中的随机游走。虽然看起来很复杂，其实这个问题数学上可以化归为跑两次 sum-product 算法。和已有算法相比，sGNN-LRP 不仅能找到最准确的贡献，而且跑得跟普通的 GNN 一样快。未来解释 GNN 模型的工具就是它了！

对了，随机游走比普通的点或者边 feature 具有更强的表达能力不是什么新鲜事了。去年 NeurIPS 的工作 NBFNet [58] 就是用随机游走定义两个点之间的关系，并且也是用动态规划解决随机游走的复杂度问题。NBFNet 当时靠这个取得了 transductive 和 inductive setting 下，多个数据集上逆天的 SotA 性能。

Miao 等人 [51] 从另一个角度出发，研究了直接可解释的 GNN 模型。他们指出诸如 GNNExplainer [53] 等 post-hoc 解释算法，由于用一个固定死的 GNN 模型，是存在一定问题的。他们觉得一个同时学习预测任务和解释的 GNN 模型，效果能更好。

从这个角度出发，他们从图 information bottleneck 原理出发，推导出了 graph stochastic attention（GSAT） [59] 。GSAT 模型先 encode 输入图，然后从后验分布中采样一个子图（解释图），并根据这个子图进行预测。相比 post-hoc 解释算法，这样做的一个好处是不需要对解释图的大小做任何限制。

▲ GSAT模型。来源：Miao等人[51]

GSAT 在实验中比 post-hoc 解释算法不仅预测点数高，解释质量也更好。此外，GSAT 也可以套在一个预训练好的 GNN 上，把它 finetune 成一个可解释模型。如果你的任务需要一个直接能解释的 GNN 模型，可以试试 GSAT。

图增强和邻域采样

今年 ICML 有些超越简单的点或边扰动的图 augmentation 方法，为 GNN 自监督训练提供了不错的工具。

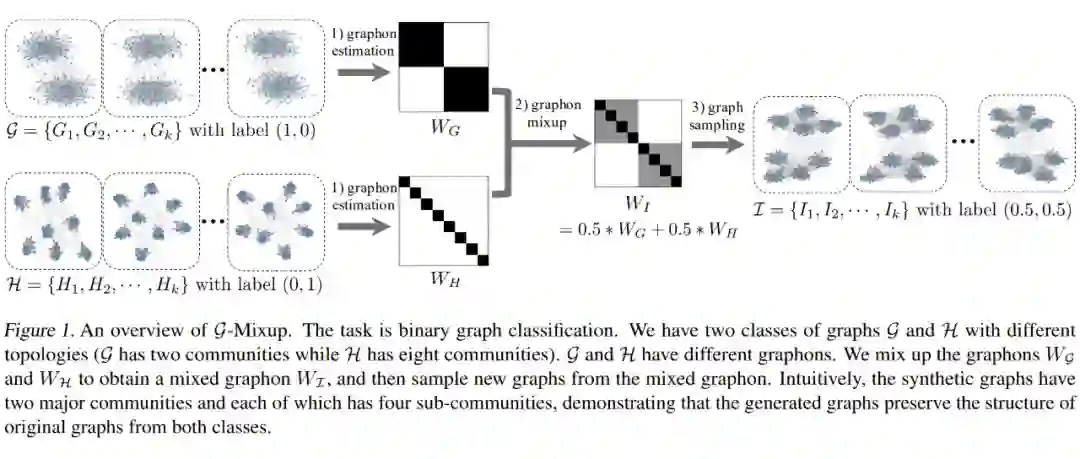
Han 等人 [60] 借鉴图像增强的 mixup 方法 [61]，提出了 G-Mixup。这篇论文也是 ICML 2022 的 Oustanding Paper Award 得主之一。Mixup 早在 2017 年就有了，其思想是对于两张图像，把它们的 feature 混合插值，同时把它们的标签混合插值（有一个可调节的混合比例），然后让模型根据插值输入预测插值输出。Mixup 能提高模型的鲁棒性和泛化能力。

但如何对两张点数和边数不同的图进行混合插值呢？

这篇论文给出了一个精妙的解法：与其混合图，不如混合 graphon。简而言之，graphon 可以理解为图的生成器。如果两张图由同一个生成器生成，它两的 graphon 就相同。有了 graphon [35]，解法就很简单了：1）对于两张图，我们求解它们的 graphon；2）我们对两个 graphon 进行插值得到一个新的 graphon；3）根据新的 graphon 采样得到一个图和它的标签；4）把图和标签扔到模型里进行训练。

在下图所示的例子里，两张图分别有 2 个和 8 个强连通分量。将它们的 graphon 混合后，我们得到了一张具有 2 个大 community，每个 community 里又有 4 个小 community 的图。Graphon 的求解有很多不同的方法，性能和复杂度也有所不一，文章里主要使用的是 largest gap 算法。

▲ G-Mixup方法。来源：Han等人[60]

G-Mixup 跟传统的点或者边扰动算法取得了相近的性能，但在高噪声环境下有着更鲁棒的效果。众所周知，图增强远比图像增强难得多，而 G-Mixup 成功把图像增强的知名算法用到了图上 ！如果你对 mixup 感兴趣的话，ICML 还有两篇工作：mixup 与标定 [62]，mixup 与生成模型 [63]。

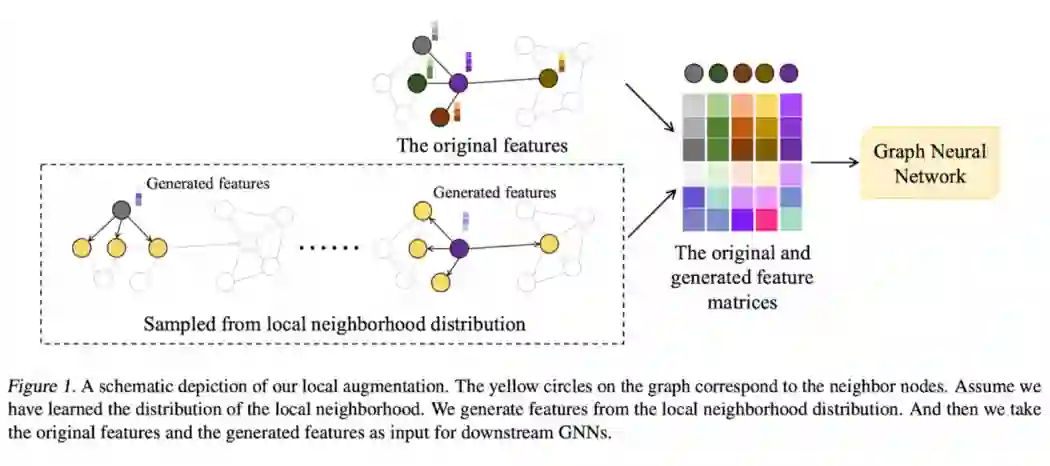
Liu 等人 [64] 则提出了 Local Augmentation GNNs [65]（LA-GNN）处理点的邻域较小的情况下的增强，其核心思路是用一个生成模型给每个点产生额外的 feature。他们在全图上训了一个 conditional VAE，用于根据每个点预测其邻居的 feature。有了这个 CVAE 后，我们只需要把一个点的 feature 输入进去，就能得到其邻居的增强 feature。

点的 feature 和增强 feature 可以一起用在 GNN 和下游任务中。CVAE 可以脱离 GNN 单独训练，然后固定 CVAE 训练 GNN 和下游任务。有趣的是，CVAE 是可以用于没见过的图的，也就是说这类 local augmentation 是 inductive 的！实验表明，这类增强确实适合度数较小的点的。

▲ 图局部增强算法。来源：Liu等人[64]

下一篇是 Yu，Wang 和 Wang 等人 [66] 提升 GNN 速度的工作。普通的邻域采样算法，例如 GraphSAGE，会导致邻域以指数速度增长和过时的历史 embedding。这篇论文则是提出了 GraphFM，利用 momentum 和 1-hop 邻域来更新每个点的历史 embedding。在此之前，momentum 常用于各种自监督学习算法中（BYOL [67]，BGRL [68]）来更新 target 模型的参数。这篇论文则是用 momentum 来降低不同 mini-batch 之间历史 representation 的方差，并为不同邻域大小的 feature 更新进行无偏估计。

GraphFM 提供了两种模式，GraphFM-InBatch 和 GraphFM-OutOfBatch：1）GraphFM-InBatch 适用于 GraphSAGE 风格的采样，可以大幅减少所需的邻居数目。GraphSAGE 一般每层需要扩展 10-20 个邻居，而 GraphFM 每层每个点只需要扩展一个邻居。没错，一个！2）GraphFM-OutOfBatch 则基于 GNNAutoScale。它先将整张图划分成 k 个 minibatch，再进行采样。

实验表明，feature momentum 对 GraphSAGE 风格的采样有奇效（in-batch版）。如果你用基于邻域采样的 GNN，可以考虑用 GraphFM 作为默认实现！

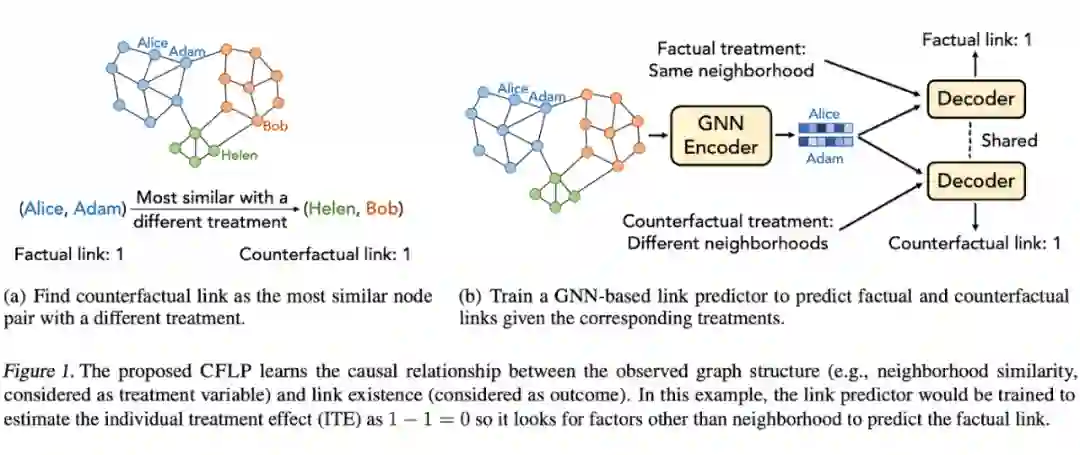
最后是 Zhao 等人 [69] 为链路预测设计的一种取巧的增强方式。这篇论文使用了 counterfactual 的边进行增强，用论文中的一句话来概括就是：

如果整张图的结构发生了变化，这条边还会存在吗？

我们希望找一些邻域结构上相似的（有很多方式可以定义相似，例如 SBM 聚类，k 核分解，Louvain 方法等等），但链路预测结果不同的边。这篇论文猜想，如果一个 GNN 能正确地区分真实的边和 counterfacutal 的边，那模型大概率能学到一些有意义的链路预测 feature，而不是 encode 一些虚假相关的 feature。

有了 counterfactual 边之后（根据所选的相似函数，可以预处理出来），CFLP [70] 先在真实的边和 counterfactual 边上进行训练，然后结合一些类平衡 loss 和正则 loss 对链路预测进行 finetune。某种程度上，这有点像在生成 hard negative 样本，加大正负样本之间的分类难度。

CFLP 在 Cora/Citeseer/PubMed 三个数据集上大幅超过了普通 GNN 的链路预测效果，并且至今还在 OGB-DDI 的榜单 [71 ] 里处于前三的水平！

▲ Counterfactual边（右）。来源：Zhao等人[69]

算法推理和图论

今年算法推理领域有个重磅炸弹：DeepMind [72] 提出的 CLRS benchmark 数据集 [73]（注：CLRS 是《算法导论》的缩写）。CLRS 涵盖了 30 个经典算法（排序、搜索、最小生成树、最短路、图论、动态规划等等），仿佛把 ICPC 的出题器交给了算法推理模型。做算法推理的同学再也不需要自己构造 toy 数据集了。

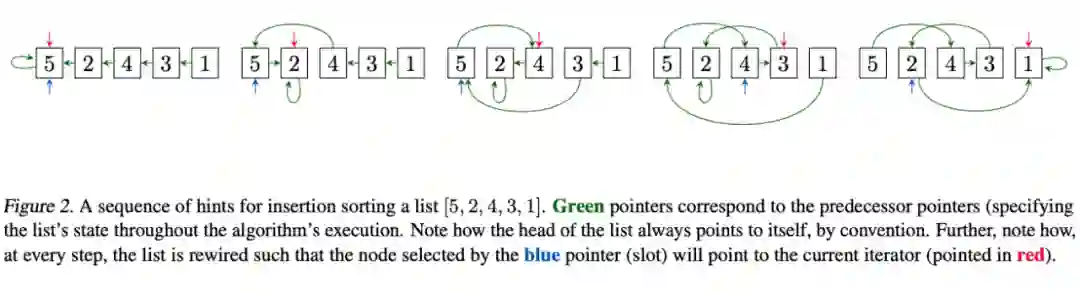
在 CLRS 数据集里，每个样本是一个 trajectory，涵盖一个算法执行的输入、输出和所有中间结果。每个样本作为一组点进行存储（有些算法不涉及边，因此不一定是图），比如对 5 个元素的排序可以看作一个 5 个点上的操作。每个 Trajectory 由多个 probe 组成，每个 probe 是一个记录当前算法执行状态的一个元组，包含算法的阶段、指针的位置、操作类型和操作的值。根据操作类型，我们决定是否输出结果。下面这个例子展示了插入排序中的指针变化。

为了测试模型的 OOD 能力，训练集和验证集的 trajectory 均包含 16 点（即 16 个元素的排序问题），但是测试集里的样本包含 64 个点。有趣的是，简单的 GNN 或者 MPNN 都能很好的拟合训练集，但是在 OOD 上一塌糊涂。Pointer Graph Network [74] 则能在 OOD 上取得好一点的成绩。可能这又是一个 GNN 不能泛化到更大图上的例子吧，虽然目前大家还不知道怎么解决这个。代码已在 GitHub 上开源 [73] ，并且能扩展支持更多的算法任务。

▲ CLRS中的trajectory。来源：Veličković等人 [72]

接下来是个更算法理论的工作，Sanmartín 等人 [75] 根据 Algebraic Path Problem（APP）发明了一些新的图上的 metric。APP 是一个用半环 [56] 代数结构统一最短路，commute time distance 以及 minimax distance 的理论框架（NBFNet [58] 里用同样的理论框架处理知识图谱推理），跟抽象代数中的范畴论也有一定关系 [76] 。举个例子，最短路是用 min 和加法作为算子，正无穷大和 0 作为零元的一种 APP。

这篇论文中基于 APP 的框架提出了一类 log-norm 距离。log-norm 距离由两个超参控制，在特定超参组合下，可以变成最短路、commute time distance 或者 minimax distance。一言蔽之，我们可以通过调节这两超参，控制这个 metric 是更像最短路还是更像 commute time distance。尽管这篇论文没有任何实验，这篇论文的理论贡献还是值得肯定的。如果你想啃范畴论的话，这篇文章值得一读，对 GNN 的应用肯定有所启发！

▲ Log-norm距离。来源：Sanmartín等人 [75]

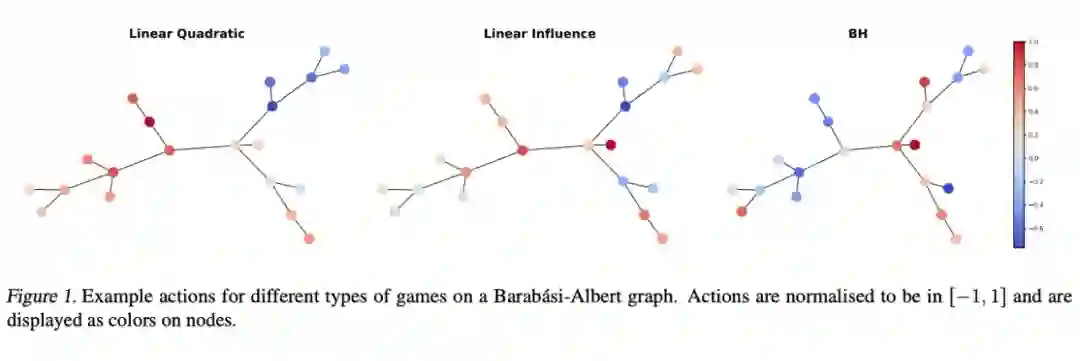
最后我们提一下 Rossi 等人 [77] 结合图论和博弈论的工作：Learning to Infer Structures of Network Games。即便你没看过博弈论，我们猜你多半听说过纳什均衡 [78]，那是非合作博弈问题的一种解。这篇论文里考虑了三类博弈游戏：linear quadratic，linear influence 和 Barik-Honorio graphical。通常我们用效用函数来定义一个游戏，但在这篇工作里，我们假设我们完全不知道效用函数。

我们把一张 N 个点的图看作 N 个人的一个游戏。在这个游戏里，每个人可以进行操作（可以把操作当作一种数值 feature，见下图），而操作会影响跟他在图中相邻的人。任务是给定每个人的操作，重构整个图的结构。这可以看作一种图生成问题：给定点 feature ，预测一个邻接矩阵  。

对于每个游戏（即每个图），我们玩 K 次，每次游戏是完全独立的。因此，我们需要模型能够对 K 个游戏具有 permutation invariant 的特性，对每个游戏内的点具有 permutation equivariant 的特性。论文提出了 NuGgeT（注：与炸鸡块同名）模型，用 Transformer 来 encode N 个人的 K 次游戏得到 latent representation，用 MLP 对每一对 latent representation decode 得到边的预测。整个模型对 K 次游戏是 permutation invariant 的。

NuGgeT 在合成数据集和真实数据集上都有不错的效果。你肯定觉得这种文章不会出现在 ICML，但它确实在那，让我们开了眼界，也让我们了解了很多有趣的概念。

▲ 来源：Rossi等人 [77]

知识图谱推理

知识图谱算是图机器学习算法的老牌试验田了，今年 ICML 也不乏有很多有趣的知识图谱推理工作。一个明显的趋势是 GNN 和逻辑规则（GNN 某种程度上也是在学逻辑规则 [79]）在逐渐取代 embedding 算法（TransE [80]，ComplEx [81]，RotatE [82]，HAKE [83]）。今年有四篇基于 GNN 或逻辑规则的文章，两篇 embedding 相关的文章。

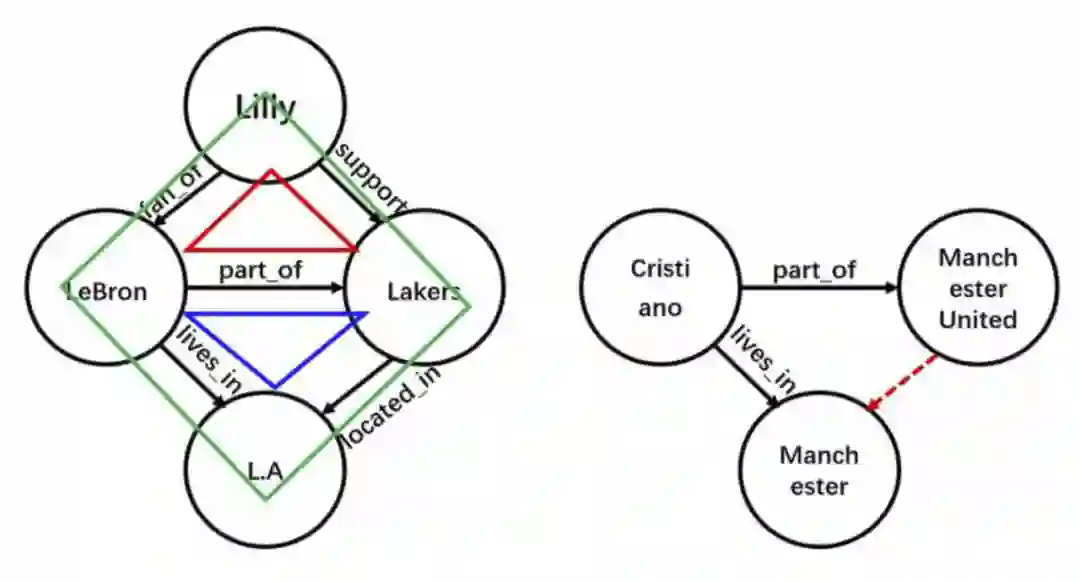
首先我们来看 Yan 等人 [84] 提出的 cycle basis GNN [85] （CBGNN）。这篇论文观察到了一个很有意思的点，在一个链式的逻辑规则中，逻辑表达式的两端恰好构成了知识图谱中的一个环结构。比如下面右图展示了逻辑规则  (X, part of Y) ∧ (X, lives in, Z) → (Y, located in Z)  对应的环。换言之，可以用一个环的置信度，来衡量一个逻辑规则是否成立。于是推理的问题转化为了学习环的 representation 的问题。

▲ 在左图中，一共有红蓝绿三个环。来源：Yan等人 [84]

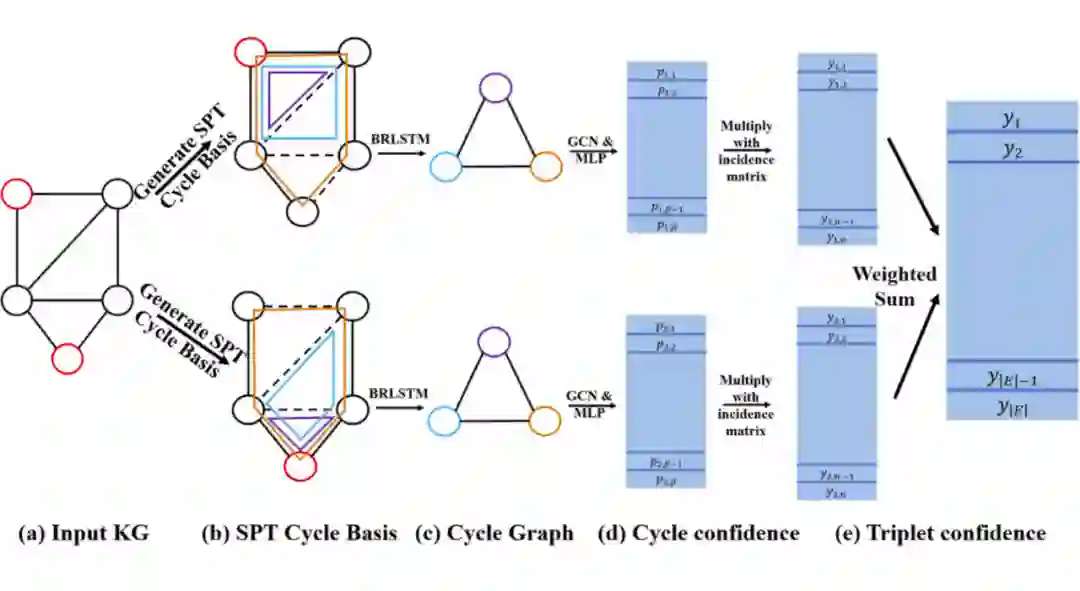
一个很有意思的性质是，环在模 2 加法和乘法下构成一个线性空间。在上面这个例子中，红环和蓝环相加，消去它们的公共边，得到绿环。因此，我们不必对每个环计算 representation，而是只要学一部分基环的 representation 即可。论文通过多个最短路径树来生成尽量短小的环。有了环之后，我们创建一个环图，其中每个点是原图中的一个环，每条边表示两个环在原图中有公共边。然后我们在这个环图上跑 GNN，即可得到原图中环的 representation。

▲ CBGNN模型。来源：Yan等人

CBGNN 的输入采用一个双向 LSTM encode 环里所有 relation，因此它学得的 representation 是 inductive 的。CBGNN 在 inductive 版本的 FB15k-237、WN18RR 和 NELL-995 数据集上都取得了 SotA 的成绩。

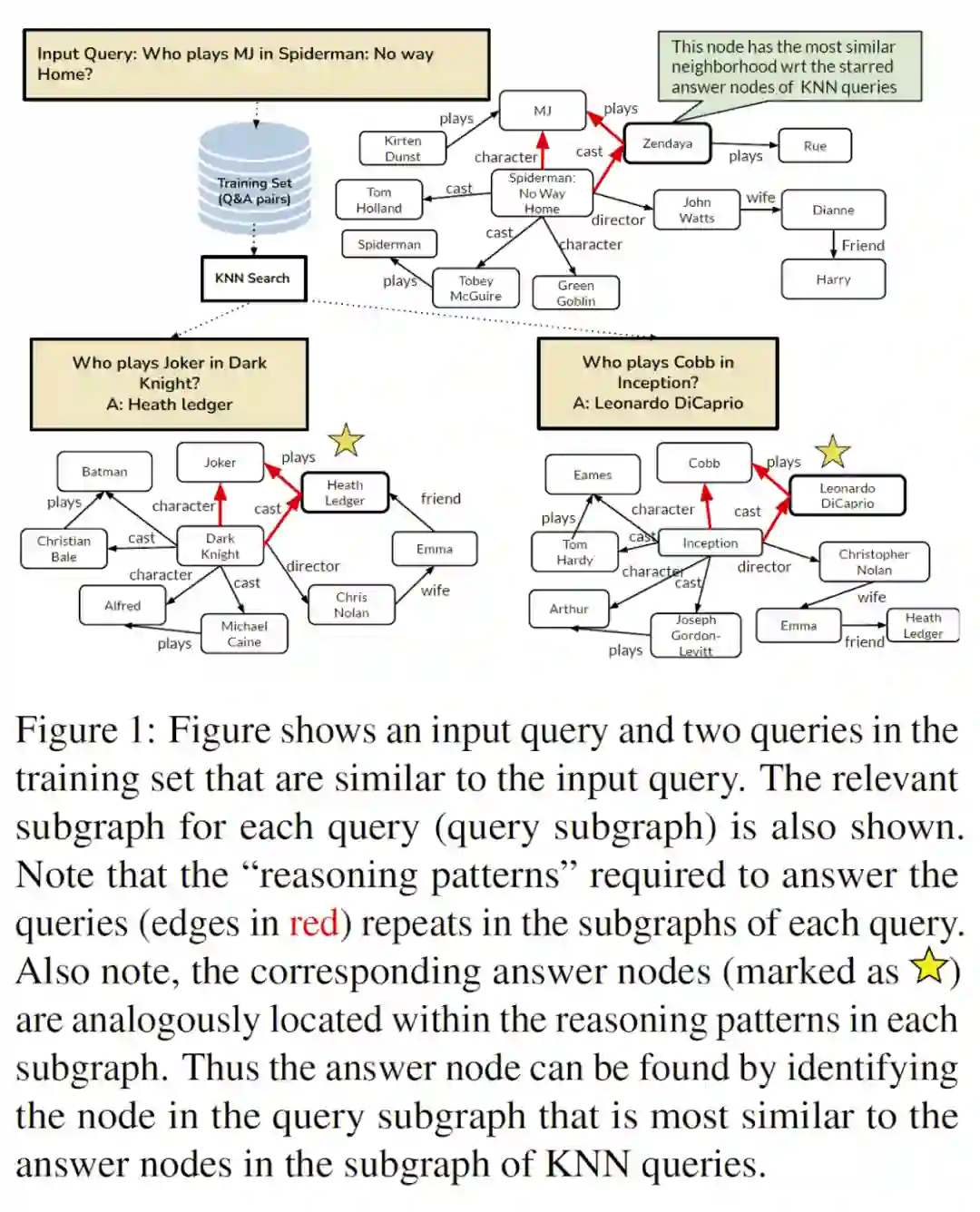
下一篇是 Das 和 Godbole 等人 [86] 提出的 CBR-SUBG [87]。CBR-SUBG 用 case-based reasoning（CBR）方法求解知识图谱问答，其核心思想是从训练集中检索跟当前问题相似的样本。我们知道这种基于检索的方法在 OpenQA 中是非常常见的（EMDR [88]，RAG [89]，KELM [90]，Mention Memory LMs [91]），不过这还是我们第一次在图上见到这种用法。

给定一个自然语言问题，CBR 首先用一个预训练语言模型得到它的 representation，并以此检索相似的 kNN 问题。由于所有检索到的样本都是训练集中的，我们可以取得这些样本对应的答案。对于每个样本，我们抽取一个包含问题 entity 和答案 entity 的局部子图。我们认为这个局部子图涵盖了预测答案所需的 pattern（尽管不一定完全准确）。

对于当前问题而言，我们没法获得答案 entity，就根据其 kNN 问题的局部子图里出现的 relation 路径类型，来抽取一个类似的局部子图。对于这  个子图，CBR-SUBG 对每张图跑一遍 GNN，然后对比当前图的 entity representation 和 kNN 问题中的答案 representation，预测得到答案。

▲ Case-based reasoning示意图。来源：Das和Godbole等人 [86]

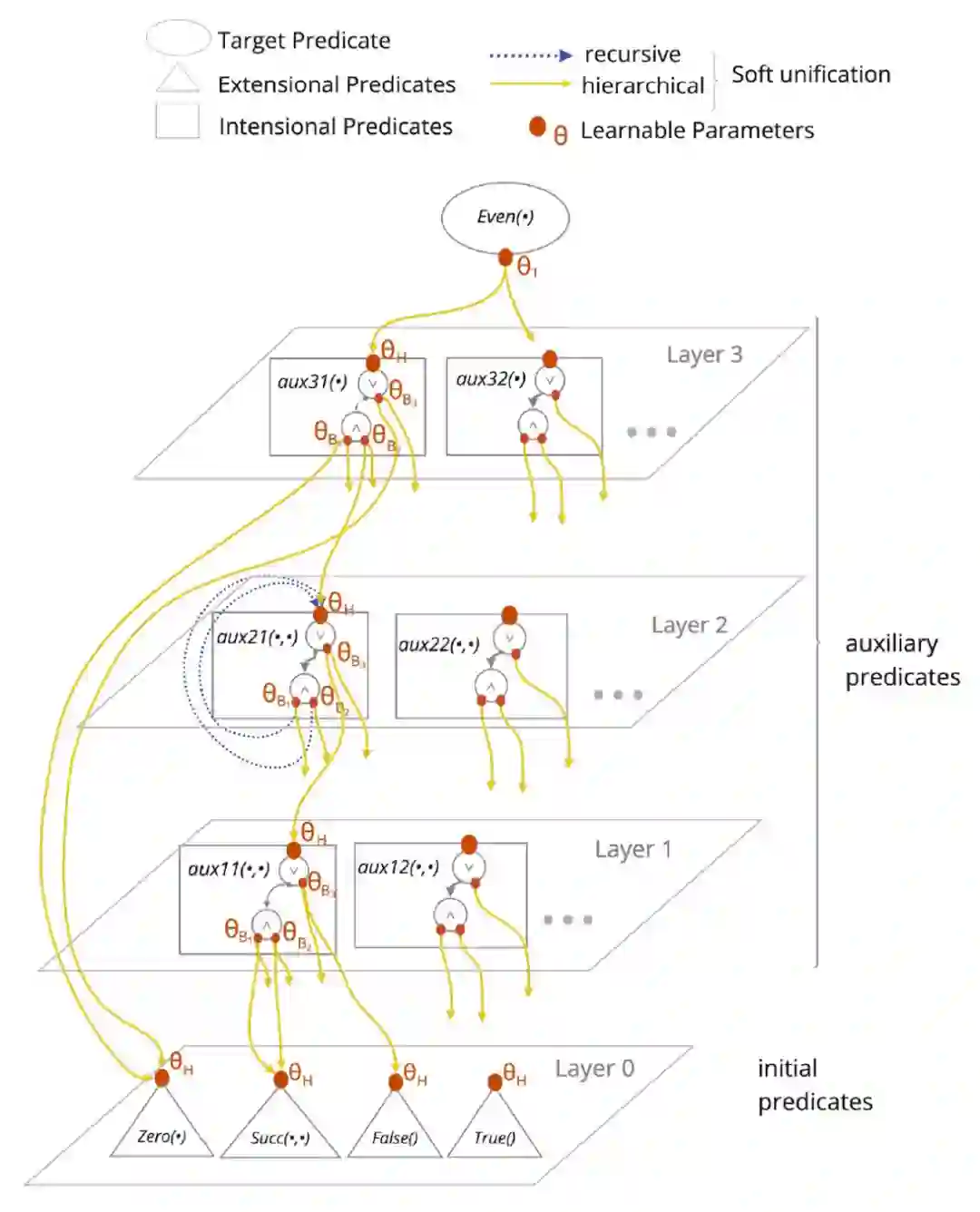
今年有两篇 neural-symbolic 类的推理工作。第一篇是 Glanois 等人 [92] 的 hierarchical rule induction [93]（HRI）。HRI 改进了 inductive logic programming 上的 logic rule induction [94]（LRI）方法。Rule induction 是指从数据中学得一系列 rule，然后用类似 forward chaining 的算法推出更多 fact。

在 LRI 和 HRI 中，每个 fact P(s,o) 由一个谓词 embedding 和一个概率  表示。每个逻辑规则  P(X,Y) ← P1(X,Z) ∧ P2(Z,Y)  由其谓词的 embedding 表示。我们想做的是不断使用 rule，得出新的 fact。在每轮迭代中，我们根据谓词的 embedding 对 rule 和 fact 进行 soft unification，看哪些 fact 的组合满足哪些 rule。当我们找到一个 rule 和它对应的若干 fact 时，我们就能根据 rule 得到一个新的 fact，并把它加入到 fact 的集合中。soft unification 以及所有谓词 embedding 都是根据观测到的 fact，end-to-end 训练得到的。

HRI 在 LRI 基础上做了三个改进：1）用一个层次化先验，在每轮迭代中学习不同的 rule；2）用 gumbel softmax 学 soft unification 中稀疏的选择操作，从而具有可解释性；3）证明了 HRI 可以表达的等效的 rule 的集合。

▲ HRI示意图。来源：Glanois等人 [92]

第二篇 neural-symbolic 的工作是来自 Zhu 等人 [95] 的 GNN-QE（利益相关：本文作者的工作）。GNN-QE 结合 GNN 和 fuzzy set 来解决知识图谱上的多跳逻辑问题。它既有 neural 的优点（比如强大的性能），又有 symbolic 的优点（比如可解释性）。由于 GNN-QE 里面有意思的东西太多了，我们打算之后单独写一篇文章来介绍 GNN-QE。朋友们，敬请期待！

最后我们想介绍的是 Kamigaito 和 Hayashi [96] 研究知识图谱 embedding 中 negative sampling 的工作。自 RotatE [82] 开始，几乎所有知识图谱 embedding 都用 margin binary cross entropy 作为 loss，并在 loss 中对 negative sampling 进行归一化。熟悉 word2vec [97] 的同学都知道，这其实和原版的 negative sampling 并不一样。

这篇论文证明了对基于距离的模型（TransE [80] ，RotatE [82] ）而言，要想达到最优解，必须要使用带归一化的 negative sampling loss。margin 超参对基于距离的模型来说也是非常重要的。只有当 margin 时，embedding 训练才有可能能达到最优解。这个和实验中观测到的现象是完全一致的。有了这篇文章的结论，我们再也不用愁如何在 embedding 方法中调 margin 了！

计算生物

计算生物的论文在今年 ICML 里也不少见。这里让我们来看看 molecular linking，protein binding，conformer generation 和 molecular property prediction 上都有哪些新工作。

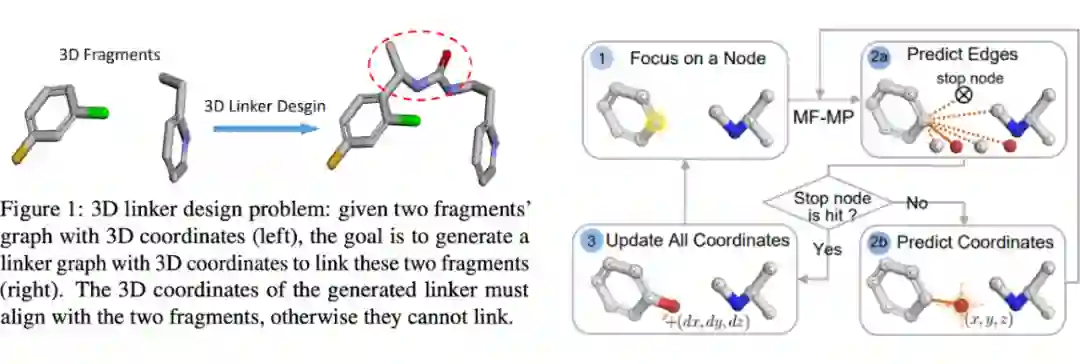
Molecular linking 是设计 Proteolysis targeting chimera（PROTAC）[98] 类药物的中重要的一个环节。对我们没有生物背景的 GNN 研究者来说，这个任务相当于给定两个分子，生成一个 linker 分子把两个分子桥接成一个分子，同时尽可能保持两个分子原有的性质（下图是一个不错的例子）

Huang 等人 [99] 提出了 3DLinker，基于 E(3)-equivariant 生成模型（VAE）逐步生成 linker 分子中每个原子和键的绝对坐标。通常，equivariant 模型是用来生成相对坐标或者相对距离矩阵的，但这篇论文里用它来生成绝对的 (x, y, z) 坐标。为了使模型根据 equivarint（坐标）和 invariant（点 feature）输入生成准确坐标，论文利用 Vector Neurons [100]（一种 ReLU 加正交投影的 trick）来确保 feature 的 equivariance。

Encoder 部分用一个 E(3)-equivariant 模型和 Vector Neurons 来 encode feature 和坐标，而 decoder 部分按以下步骤依次生成 linker 分子：

1. 在输入分子上挑一个 anchor 原子，与 linker 分子相连；

2. 预测 linker 分子中一个原子的类型；

3. 预测  linker 分子中的键和绝对坐标；

4. 重复上述步骤直到预测的原子类型为停止符为止。

3DLinker 是目前第一个不需要知道 anchor 原子（之前的模型都需要给定 anchor 原子）就能预测 linker 分子准确 3D 坐标的模型，并且在实验上取得了相当棒的效果。

▲ 3DLinker示意图。来源：Huang等人 [99]

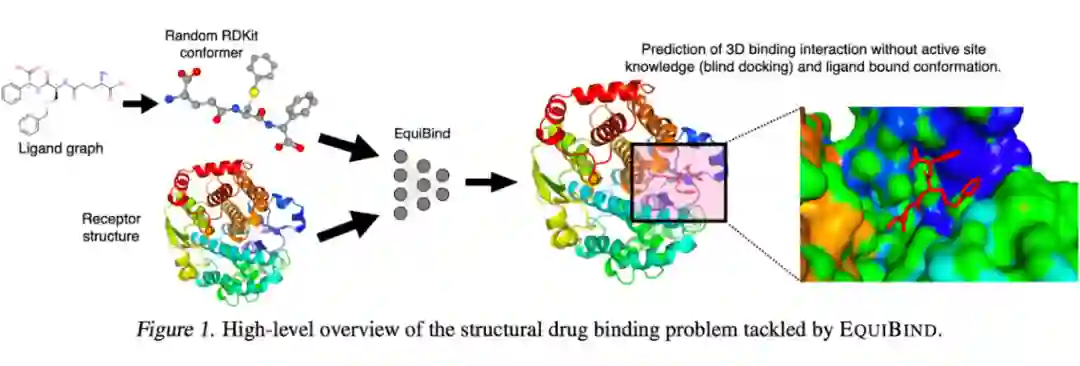
另一个重要的药物发现任务是 protein-ligand binding，即预测小分子能和大蛋白的哪个区域结合。Stärk 和 Ganea等人 [101] （Ganea 大佬一路走好）提出了 EquiBind 模型。EquiBind 模型输入一个 protein 和一个 RDKit 库计算得到的 ligand 的 conformer，输出 binding interaction 在 3D 空间中的位置。EquiBind 在 Youtube 上有视频讲解 [102] ，MIT News [103] 对 EquiBind 也有一篇报道。我们非常推荐你仔细看一下这篇论文的内容！Equibind 相比商业软件来说快了好几个数量级，同时预测质量也非常高。

▲ EquiBind示意图。来源：Stärk和Ganea等人 [101]

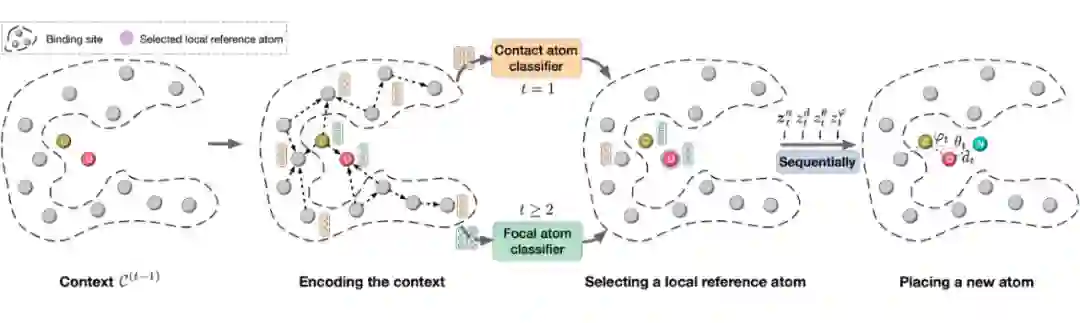
如果我们不知道 binding 用的分子长什么样的话，可以用 Liu 等人 [104] 提出的 GraphBP [105] 来预测这个分子。GraphBP 是一个 autoregressive 的分子生成方法。给定一个目标 protein site，GraphBP 用一个 3D GNN（SchNet [106] ）来 encode protein 的结构，然后不断生成原子类型和球面坐标，直到无法生成更多原子。当所有原子生成完后，论文使用 OpenBabel [107] 库来计算得到所有键。

▲ GraphBP生成binding分子的过程。来源：Liu等人 [104]

在 molecular property prediction 任务上，Yu 和 Gao [108] 提出了一种简单有效的改进分子 representation 的方式。具体来说，论文先从训练集中抽取了一套 motif 词典，并根据 TF-IDF [109] 对 motif 进行排序（NLP 乱入）。然后，每个分子可以看作若干 motif 的并集，整个数据集则可以看作一个分子和 motif 的 heterogeneous 图：如果某个分子包含某个 motif，那它两就有一条边。如果两个 motif 至少在一个分子中共用过边，那它两就有一条边。我们用 TF-IDF 作为图中边上的 feature。

有了这个分子和 motif 的图后，每个分子的 representatoin 就变成了一个正常分子 GNN 的到的 representation，外加这个 heterogeneous 图上得到的分子的 representation。

这篇文章提出的 Heterogeneous Motif GNN [110]（HM-GNN）全方位超过数 k 环 motif 的 Graph Substructure Network [111]（GSN），甚至超过了顶尖的高阶 message passing 模型 Cell Isomorphism Network [112]（CIN）。估计日后高阶 GNN 的研究中，HM-GNN 是一个简单而又强大的 baseline。

▲ HM-GNN中创建motif词典的步骤。来源：Yu和Gao [108]

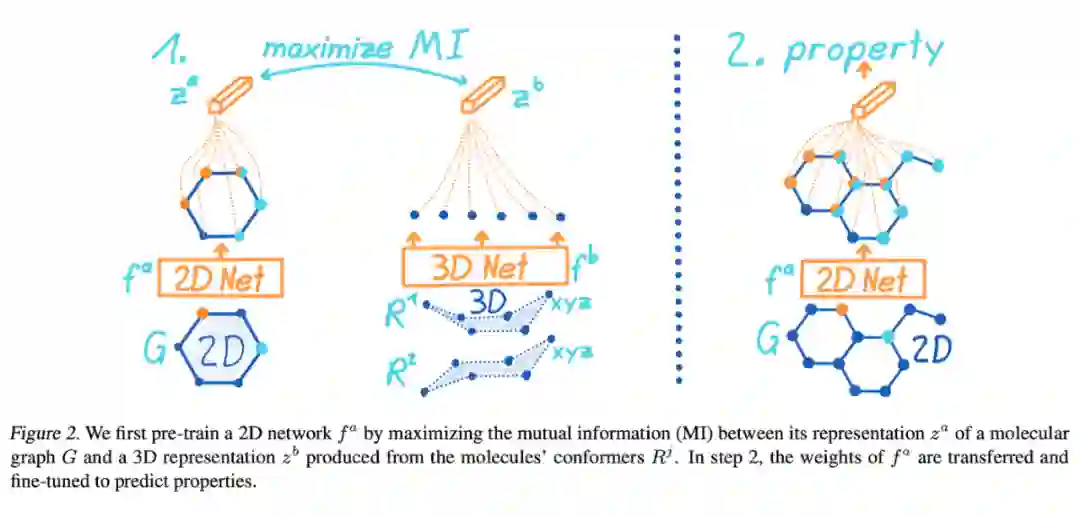
最后一篇是 Stärk 等人 [113] 在 2D 分子图和 3D conformer 上 pretrain GNN 的 3D Infomax 算法。顾名思义，3D Infomax [114] 希望最大化 2D representation 和 3D representation 之间的互信息，这样在测试的时候，即便是只输入 2D graph，模型也能隐式地表达一些 3D 信息。

具体来说，3D Infomax 中用 Principal Neighborhood Aggregation [115] （PNA）模型来 encode 2D 输入，用 Spherical Message Passing [116] （SMP）来 encode 3D 输入。我们将 2D 和 3D representation 的 cosine 相似度输入到 contrastive loss 中，最大化正样本对之间的互信息，同时最小化负样本对之间的互信息。预训练好 2D 和 3D 模型后，我们就可以在下游任务上 finetune 2D 模型了，比如 QM9 数据集。

对了，如果你感兴趣分子上的 pretrain GNN，也许可以看看 ICLR 2022 的 GraphMVP [117]。GraphMVP 也用 2D 和 3D 信息进行 pretrain。

▲ 3D Infomax先pretrain 2D和3D模型，然后在下有任务上finetune 2D模型。来源：Stärk等人[113]

图的应用场景

GNN 为物理模拟和分子动力学带来了很大的突破。一种常见的物理模拟任务是预测一个粒子系统中粒子随时间的运动轨迹，其中点 feature 记录粒子在历史时间中的运动速度，边 feature 表示粒子之间相对距离的变化。

今年，Rubanova 和 Sanchez-Gonzalez 等人 [118] 提出了 Constraint-based Graph Network Simulator（C-GNS），在物理模拟任务中显示地加入标量约束条件。

粗略来讲，在粒子过了 MPNN encoder 之后，我们把粒子的信息放到一个能求解约束条件的模型中。求解模型本身是一个可微函数（文章中实际是个 5 步 gradient descent），换言之我们可以通过求解模型进行反传。C-GNS 本质上属于一种 deep implicit layer [119]，这类方法最近在 GNN 中越来越常见了。

物理模拟最 fancy 的部分当然是可视化了！来看看作者们提供的 demo [120] 吧。

▲ Constraint-based Graph Network Simulator示意图。来源：Rubanova和Sanchez-Gonzalez等人 [118]

其他值得看一看的应用场景还有：

交通预测：Lan 和 Ma 等人 [121] 提出了 Dynamic Spatial-Temporal Aware Graph Neural Network [122]（DSTA-GNN）。继去年 DeepMind 在 Google Map 中用 GNN 来预测到达时间 [123] 后，这篇文章在加州道路数据上预测交通流量。

神经网络剪枝：Yu 等人 [124] 提出了 GNN-RL [125] 来逐步删减深度网络中的权重，直到达到给定的 FLOPs。这篇论文把整个神经网络的计算图当做一个层次化的图，并用层次化的 GNN 方法 encode 这张图。在 GNN 得到的 representation 的基础上，论文使用一个 RL agent 来决定删减哪部分权重。

排序问题：He 等人 [126] 研究了一个有趣的问题：给定一个两两交互的矩阵（例如足球联赛中球队之间的净胜球数），求解点（球队）的排名。换句话说，这相当于知道了循环赛的比分后，预测哪支球队是冠军。论文提出了 GNNRank 来 encode 两两交互的矩阵，并计算对应图 Laplacian 的 Fiedler vector [127]。

非常感谢你能读到这里，看完了满满干货！😅

几个月后让我们 NeurIPS 和 LoG 再见！

参考文献

[1] https://icml.cc/Conferences/2022/Schedule?type=Workshop

[2] https://arxiv.org/abs/2006.11239

[3] https://arxiv.org/abs/2112.10741

[4] https://openai.com/dall-e-2/

[5] https://gweb-research-imagen.appspot.com/paper.pdf

[6] https://arxiv.org/pdf/2205.09853.pdf

[7] https://arxiv.org/pdf/2205.14217.pdf

[8] https://arxiv.org/pdf/2205.09991.pdf

[9] https://arxiv.org/pdf/2203.17003.pdf

[10] https://arxiv.org/pdf/2102.09844.pdf

[11] https://github.com/ehoogeboom/e3_diffusion_for_molecules

[12] https://www.notion.so/ICML-2022-40a7967f468f41959756ffbe15306fae

[13] https://twitter.com/emiel_hoogeboom/status/1509838163375706112

[14] https://arxiv.org/pdf/2202.02514.pdf

[15] https://openreview.net/pdf?id=PxTIG12RRHS

[16] https://en.wikipedia.org/wiki/Wiener_process

[17] https://openreview.net/pdf?id=JHcqXGaqiGn

[18] https://en.wikipedia.org/wiki/Langevin_dynamics

[19] https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods

[20] https://github.com/harryjo97/GDSS

[21] https://arxiv.org/pdf/2204.01613.pdf

[22] https://github.com/KarolisMart/SPECTRE

[23] https://en.wikipedia.org/wiki/Stiefel_manifold

[24] https://papers.nips.cc/paper/2019/file/bb04af0f7ecaee4aae62035497da1387-Paper.pdf

[25] https://arxiv.org/pdf/2202.03036.pdf

[26] https://arxiv.org/pdf/2107.07999.pdf

[27] https://arxiv.org/abs/2009.14794

[28] https://proceedings.mlr.press/v162/papp22a/papp22a.pdf

[29] https://towardsdatascience.com/using-subgraphs-for-more-expressive-gnns-8d06418d5ab

[30] https://proceedings.mlr.press/v162/huang22l/huang22l.pdf

[31] https://openreview.net/forum?id=BJluy2RcFm

[32] https://github.com/zhongyu1998/PG-GNN

[33] https://proceedings.mlr.press/v162/cai22b/cai22b.pdf

[34] https://arxiv.org/abs/1812.09902

[35] https://en.wikipedia.org/wiki/Graphon

[36] https://twitter.com/ChenCaiUCSD/status/1550109192803045376

[37] https://proceedings.mlr.press/v162/gao22e/gao22e.pdf

[38] https://arxiv.org/abs/2006.10637

[39] https://openreview.net/forum?id=rJeW1yHYwH

[40] https://proceedings.mlr.press/v162/chen22o/chen22o.pdf

[41] https://github.com/chens5/WL-distance

[42] https://arxiv.org/abs/1808.04337

[43] https://tenor.com/view/predator-arnold-schwarzenegger-hand-shake-arms-gif-3468629

[44] https://proceedings.mlr.press/v162/wang22am/wang22am.pdf

[45] https://en.wikipedia.org/wiki/Jacobi_polynomials

[46] https://proceedings.neurips.cc/paper/2016/file/04df4d434d481c5bb723be1b6df1ee65-Paper.pdf

[47] https://en.wikipedia.org/wiki/Chebyshev_polynomials

[48] https://proceedings.mlr.press/v162/li22h/li22h.pdf

[49] https://proceedings.mlr.press/v162/yang22n/yang22n.pdf

[50] https://proceedings.mlr.press/v162/xiong22a/xiong22a.pdf

[51] https://proceedings.mlr.press/v162/miao22a/miao22a.pdf

[52] https://arxiv.org/pdf/2006.03589.pdf

[53] https://arxiv.org/pdf/1903.03894.pdf

[54] https://arxiv.org/pdf/2011.04573.pdf

[55] https://arxiv.org/pdf/2010.05788.pdf

[56] https://en.wikipedia.org/wiki/Semiring

[57] https://github.com/xiong-ping/sgnn_lrp_via_mp

[58] https://papers.nips.cc/paper/2021/file/f6a673f09493afcd8b129a0bcf1cd5bc-Paper.pdf

[59] https://github.com/Graph-COM/GSAT

[60] https://arxiv.org/pdf/2202.07179.pdf

[61] https://github.com/facebookresearch/mixup-cifar10

[62] https://proceedings.mlr.press/v162/zhang22f/zhang22f.pdf

[63] https://proceedings.mlr.press/v162/sohn22a/sohn22a.pdf

[64] https://arxiv.org/pdf/2109.03856.pdf

[65] https://github.com/SongtaoLiu0823/LAGNN

[66] https://arxiv.org/pdf/2206.07161.pdf

[67] https://papers.nips.cc/paper/2020/file/f3ada80d5c4ee70142b17b8192b2958e-Paper.pdf

[68] https://arxiv.org/pdf/2102.06514.pdf

[69] https://arxiv.org/pdf/2106.02172.pdf

[70] https://github.com/DM2-ND/CFLP

[71] https://ogb.stanford.edu/docs/leader_linkprop/

[72] https://arxiv.org/pdf/2205.15659.pdf

[73] https://github.com/deepmind/clrs

[74] https://proceedings.neurips.cc//paper/2020/file/176bf6219855a6eb1f3a30903e34b6fb-Paper.pdf

[75] https://proceedings.mlr.press/v162/sanmarti-n22a/sanmarti-n22a.pdf

[76] https://arxiv.org/pdf/2005.06682.pdf

[77] https://arxiv.org/pdf/2206.08119.pdf

[78] https://en.wikipedia.org/wiki/Nash_equilibrium

[79] https://openreview.net/pdf?id=r1lZ7AEKvB

[80] https://proceedings.neurips.cc/paper/2013/file/1cecc7a77928ca8133fa24680a88d2f9-Paper.pdf

[81] http://proceedings.mlr.press/v48/trouillon16.pdf

[82] https://arxiv.org/pdf/1902.10197.pdf

[83] https://ojs.aaai.org/index.php/AAAI/article/view/5701/5557

[84] https://proceedings.mlr.press/v162/yan22a/yan22a.pdf

[85] https://github.com/pkuyzy/CBGNN

[86] https://proceedings.mlr.press/v162/das22a/das22a.pdf

[87] https://github.com/rajarshd/CBR-SUBG

[88] https://arxiv.org/pdf/2106.05346.pdf

[89] https://arxiv.org/abs/2005.11401

[90] https://arxiv.org/pdf/2010.12688.pdf

[91] https://openreview.net/forum?id=OY1A8ejQgEX

[92] https://proceedings.mlr.press/v162/glanois22a/glanois22a.pdf

[93] https://github.com/claireaoi/hierarchical-rule-induction

[94] https://arxiv.org/pdf/1809.02193.pdf

[95] https://proceedings.mlr.press/v162/zhu22c/zhu22c.pdf

[96] https://proceedings.mlr.press/v162/kamigaito22a/kamigaito22a.pdf

[97] https://proceedings.neurips.cc/paper/2013/file/9aa42b31882ec039965f3c4923ce901b-Paper.pdf

[98] https://en.wikipedia.org/wiki/Proteolysis_targeting_chimera

[99] https://arxiv.org/pdf/2205.07309.pdf

[100] https://arxiv.org/pdf/2104.12229.pdf

[101] https://arxiv.org/pdf/2202.05146.pdf

[102] https://www.youtube.com/watch?v=706KjyR-wyQ&list=PLoVkjhDgBOt11Q3wu8lr6fwWHn5Vh3cHJ&index=15

[103] https://news.mit.edu/2022/ai-model-finds-potentially-life-saving-drug-molecules-thousand-times-faster-0712

[104] https://proceedings.mlr.press/v162/liu22m/liu22m.pdf

[105] https://github.com/divelab/GraphBP

[106] https://proceedings.neurips.cc/paper/2017/file/303ed4c69846ab36c2904d3ba8573050-Paper.pdf

[107] https://jcheminf.biomedcentral.com/articles/10.1186/1758-2946-3-33

[108] https://proceedings.mlr.press/v162/yu22a/yu22a.pdf

[109] https://en.wikipedia.org/wiki/Tf%E2%80%93idf

[110] https://github.com/ZhaoningYu1996/HM-GNN

[111] https://arxiv.org/pdf/2006.09252.pdf

[112] https://arxiv.org/pdf/2106.12575.pdf

[113] https://proceedings.mlr.press/v162/stark22a/stark22a.pdf

[114] https://github.com/HannesStark/3DInfomax

[115] https://arxiv.org/abs/2004.05718

[116] https://openreview.net/forum?id=givsRXsOt9r

[117] https://openreview.net/forum?id=xQUe1pOKPam

[118] https://proceedings.mlr.press/v162/rubanova22a/rubanova22a.pdf

[119] http://implicit-layers-tutorial.org/

[120] https://sites.google.com/view/constraint-based-simulator

[121] https://proceedings.mlr.press/v162/lan22a/lan22a.pdf

[122] https://github.com/SYLan2019/DSTAGNN

[123] https://www.deepmind.com/publications/eta-prediction-with-graph-neural-networks-in-google-maps

[124] https://proceedings.mlr.press/v162/yu22e/yu22e.pdf

[125] https://github.com/yusx-swapp/GNN-RL-Model-Compression

[126] https://arxiv.org/pdf/2202.00211.pdf

[127] https://en.wikipedia.org/wiki/Algebraic_connectivity

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·