node2vec随机游走实现思路

会员服务 ·

node2vec随机游走实现思路

2020 年 5 月 30 日 AINLP

一言以蔽之，node2vec=动态随机游走生成sequence+skip- gram的word2vec，本文将简单聊聊如何欢快地实现动态随机游走构造sequence。

随机游走的过程

随机游走的过程，就像小时候玩跳格子游戏一样，从一个节点（格子）出发，随机选择与之“相连”的一个节点（格子）并移动到该位置，然后不断重复以上过程直至达到游走停止条件（如最大游走长度）。

[ PS : 之所以在相连一词上加引号，是因为存在下一跳节点和当前的节点不直接相连（即不存在边）的情况，例如在struc2vec游走过程中，节点的下一跳为与之结构相似的节点而非邻居节点。]

随机游走分类

随机选择节点，这句过于笼统，我们可以尝试回答一下两个问题：

Q1 : 从一个节点出发，在与之“相连”的节点集合中选择其中一个节点的概率是否相等？（等概/无偏，不等概/有偏）

Q2 : 在整个随机游走过程中，从一个节点出发到其他节点的概率会发生改变么？（不改变/静态，改变/动态）

根据node2vec论文中的定义，针对带权边的图而言，该过程是一个 「有偏的、动态的」 随机游走过程。

不同类型的随机游走的实现策略

设当前节点为v，下一跳的节点集合为S = {x0, x1, x2, t}，其中t是上一跳节点。为了方便定位，集合S实际上是个vector/array。

「Easy模式：无偏的随机游走」

假设某个节点下一跳的节点集合中共有N个节点，那么从每个节点被选中的概率均为1/N。

从 [0, N-1] 中随机选择一个整数i，S[i]即为被选中的节点。

时间复杂度：采样节点花费O(1)

空间复杂度：O(1)，无需额外空间存储

「2. Medium模式：静态、有偏的随机游走」

节点到其他节点的转移概率受边权的影响而有所不同。

设edge<v,x0>=1, edge<v,x1>=2, edge<v,x2>=2, edge<v,t>=0.5。

「PartialSum方法」

PartialSum方法将转移概率的大小分布在一个长度为1的线段上，通过在线段随机取点找到对应的节点，因为节点的转移概率不同，最快时间复杂度为O(logN)。

step1：根据边权计算转移概率P = {2/11,4/11,4/11,1/11}

step2：计算累积概率和 PartialSum = {2/11, 6/11, 10/11, 1}

step3：从[0,1]随机选择一个数，二分查找寻找对应的节点。

时间复杂度：预处理O(N)，采样节点O(logN)

空间复杂度：需额外存储一个PartialSum数组O(N)

「AliasTable方法」

要想让采样过程能够再快一些，直观的想法是我能否从[0, N-1]中随机选择一个整数i，就能直接判断S[i]能否被抽中？

首先将转移概率P想象成一个长度为1的线段，并将其复制N份，得到N个长度为1的线段

其次，这四根线段的内容进行重新排列，使每个节点都能分配到一个长度为1的线段，设第i个节点的转移概率为，复制N份后为，即可支配的长度为，我们的目标是节点i的可支配长度尽量填充节点i分配到的线段长度，如果无法占满，则从其他节点的可支配线段中削一点过来填充。

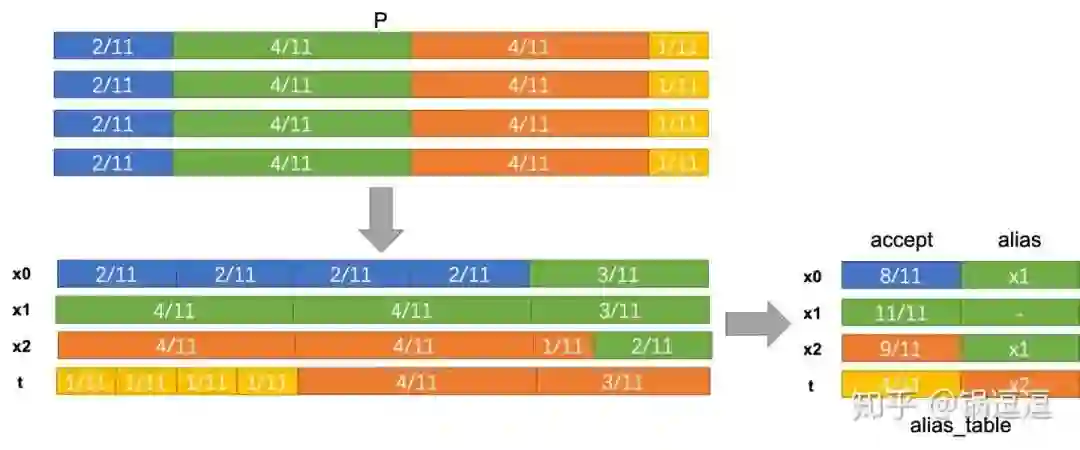
实际实现中设计了accept和alias分别维护接受当前节点概率和拒绝后应该采样的节点id。

step1：根据边权计算转移概率P = {2/11,4/11,4/11,1/11}

step2：计算accept = {8/11, 1, 9/11, 4/11}；alias = {x1, -, x1, x2}

step3：从 [0, N-1] 中随机选择一个整数i，从[0,1]随机选择一个数p；判断p<accept[i]成立，则S[i]即为被选中的节点；否则alias[i]为被选中的节点。

时间复杂度：计算AliasTable，预处理时间为O(N)，采样节点时间为O(1)

空间复杂度：需额外存储一个AliasTable，包含两个数组（accept和alias），空间为O(2N)

「3. Hard模式：动态、有偏的随机游走」

节点到其他节点的转移概率既受边权的影响，又受到转移状态的影响。

node2vec中，节点v到节点x的转移分数定义如下：

其中转移状态需要评估节点x和上一条节点t的距离。

不同于静态有偏随机游走，只需每个节点构建一个Alias Table，采样时直接查表即可。「动态有偏随机游走，需要对每条有向边（ <上一跳节点，当前节点>）构建一个Alias Table」。

若这样实现node2vec，想要在大规模网络中使用这个模型就变得有那么一点异想天开的味道。

掩卷沉思，思考以下问题：

a. 如果一个网络节点上亿，每个节点邻居数成百上千咋整？数据存得下么？预计算Alias Table的时间成本可接受？

b. 相对于网络中总的边数，随机游走能够遍历到的边非常有限，即大部分有向边计算Alias Table的计算都是无用的。计算所有边的Alias Table真的有必要么？

针对问题1，不难给出以下两种解决方案：

解决方案1：对数据做个预处理，每个节点邻居数根据转移分数取top几十可以吗？可以，这是Spark-Node2Vec的方案，是一种近似求解方案，
解决方案2：大度数节点不根据边计算Alias Table，用静态转移概率来替代？也可以，这是Fast-Node2Vec的方案，同样也是一种近似求解方案。

这两种方案治标不治本，也无法有效解决问题b。

再再回顾Easy模式，再从“从[0, N-1]中随机选择一个整数i，直接判断S[i]能否被抽中？”的思路尝试解决这个Hard模式的随机游走。

首先先对转移分数进行动静分离：转移分数 =动态转移状态

* 静态边权。

先不管静态边权的部分（或者假设边权为1），重新审视。

观察发现， 「动态转移状态的取值固定，不需要事先计算节点间的转移状态，也可以知道转移状态的最大值和最小值」 。

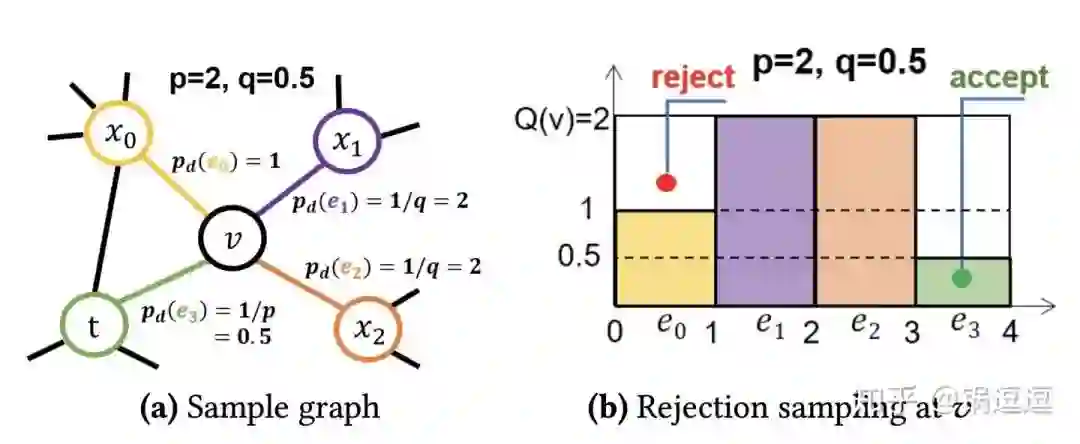
设转移状态的最大值为Tmax，最小值为Tmin，根据定义可以得

Tmax = max(1/p, max(1, 1/q))

Tmin = min(1/p, min(1, 1/q))

「无需在计算过程中对v所有邻居节点的转移状态归一化操作，因为所有的转移状态值均落于[Tmin, Tmax]区间。」

可以构建一个长为N，宽为Tmax的矩形。

从 [0, N-1] 中随机选择一个整数i，从[0,Tmax]随机选择一个数p；
根据节点S[i]和t的关系，确定对应的状态值s。
判断p<s成立，则S[i]即为被选中的节点；否则拒绝S[i]，重复step1。

上述方法无需提前计算边<v,t>的alias table，每次循环只会选中一个节点，直接判断该节点与上一跳节点满足的转移状态即可。

选中节点的期望=有效面积之和（图(b)彩色面积之和）/总面积（N *「Tmax）。有效面积占比越大，选中节点的概率越大，即越有可能一次循环就可以完成采样工作。」

存在一种很糟糕的情况：有效面积占比非常小（图(a))，针对Tmax=1/p，我们可以针对节点为t对应的小矩形块，进行裁剪操作，裁下超过Tmax'=max(1.0, 1/q)的部分，生成｜(Tmax-Tmax')/Tmax｜（向上取整）个新的都用于表示节点t的邻居节点（图(b))。

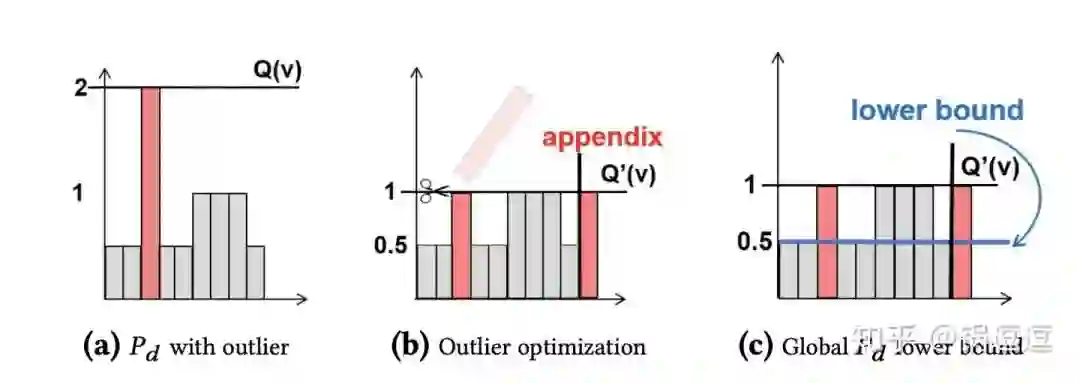
当采样概率小于Tmin时，不管当前采样节点和上一跳节点的关系如何，都可以直接接受该节点（图(c))，算是一种预处理的trick。

再回过头来考虑静态边权的部分，横轴的取值范围就不是[1,N]，而是[0,Sum_N]，其中Sum_N表示节点邻居节点的边权和，即每个样本对应的小方块，横轴为边权，纵轴为动态转移状态值。

因为横轴的转移状态是静态的，可以用Partial Sum方法，也可以直接用Alias Table方法。

时间复杂度：计算AliasTable/Partial Sum，预处理时间为O(N)，采样节点时间为O(K)，K是常数。

空间复杂度：O(2N)（Alias Table）或者O(N)（Partial Sum）。

走一步，再走一步

❝
此后，我生命中有很多时刻，面对一个遥不可及的目标，或者一个令人畏惧的情境，当我感到惊慌失措时，我都能够轻松应对——因为我回想起了很久以前悬崖上的那一课。我提醒自己不要看下面遥远的岩石，而是注意相对轻松、容易的第一小步，迈出一小步，再一小步，就这样体会每一步带来的成就感，直到达成了自己的目标。这个时候，再回头看，就会对自己走过的这段漫漫长路感到惊讶和骄傲。
——《悬崖上的一课》
❞