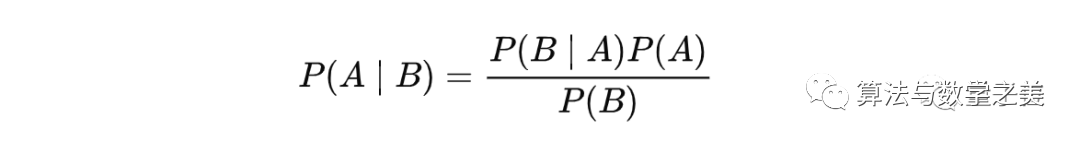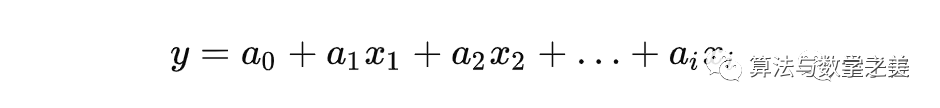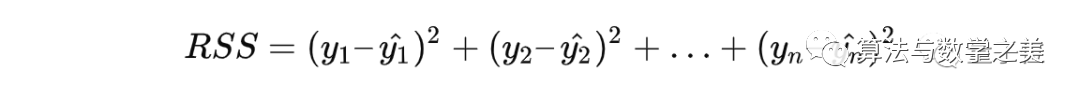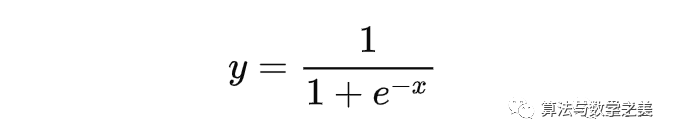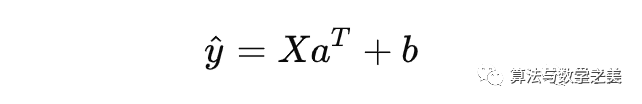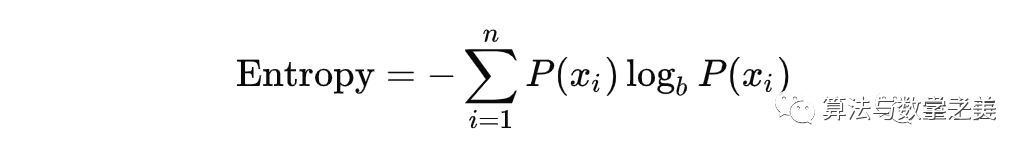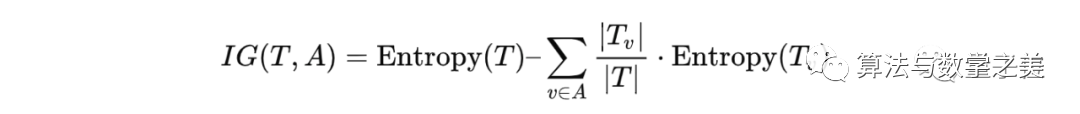数据科学中的6个基本算法，掌握它们要学习哪些知识

如果想从事数据科学，但是又没有数学背景，那么有多少数学知识是做数据科学所必须的？

统计学是学习数据科学绕不开的一门数学基础课程，但数据科学也经常会涉及数学中的其他领域。

数据科学使用算法进行预测，这些算法称为机器学习算法，有数百种之多。 有人总结了数据科学中最常用的6种算法，已经掌握它们分别需要哪些数学知识。

朴素贝叶斯分类器

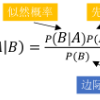
朴素贝叶斯分类器（Naive Bayes classifier）是一种简单的概率分类器，它基于特征之间相互独立的假设，以贝叶斯定理为基础。

贝叶斯定理的数学公式为：

其中A、B表示两个事件，且P(B)不等于0。 各个部分具体的含义为：

1、P(A|B)是条件概率，它是事件B发生后事件A发生的概率。

2、P(B|A)也是一个条件概率，它是事件A发生后事件B发生的概率。 事件发生的可能性 发生了 是真的。

3、P(A)和P(B)是各自发生的概率，A、B两个事件彼此独立。

需要的数学知识：

如果你想要了解朴素贝叶斯分类器，以及贝叶斯定理的所有用法，只需学习概率课程就足够了。

线性回归

线性回归是最基本的回归类型，它用来理解两个连续变量之间的关系。 在简单线性回归的情况下，获取一组数据点并绘制可用于预测未来的趋势线。

线性回归是参数化机器学习的一个例子，训练过程最终使机器学习找到最接近于训练集的数学函数，然后可以使用该函数来预测未来的结果。 在机器学习中，数学函数被称为模型。 在线性回归的情况下，模型可以表示为：

a1, a1, ……，an表示对数据集的参数值，x1, x1, ……，xn表示在线性模型中使用的特征值。

线性回归的目标是找到描述特征值和目标值之间关系的最佳参数值。 换句话说，就是找到一条最适合数据的线，可以外推趋势以预测未来结果。

为了找到线性回归模型的最佳参数，我们希望让残差平方和（residual sum of squares）最小化。 残差通常被称为误差，它用来描述预测值和真实值之间的差异。 残差平方和的公式可表示为：

y的“头顶”加上^用来表示预测值，y表示真实值。

需要的数学知识：

如果你只想粗略地了解，基础统计学课程就可以了。 残差平方和的公式可以在大多数高级统计课程中学到。

逻辑回归

逻辑回归（Logistic regression）侧重于二元分类，即输出结果只有两种情况的概率。

与线性回归一样，逻辑回归是参数化机器学习的一个例子。 因此，这些机器学习算法的训练过程的结果是找到最接近训练集的数学函数模型。

但是线性回归模型输出的是一组实数，而逻辑回归模型输出的是概率值。 在逻辑回归的过程中还会用到sigmoid函数，它会把所有值压缩到0~1的范围之间。

需要的数学知识：

这一部分包含的知识有指数函数和概率，你需要对代数和概率论有充分的理解。 如果想深入了解，建议学习概率论、离散数学或实分析。

神经网

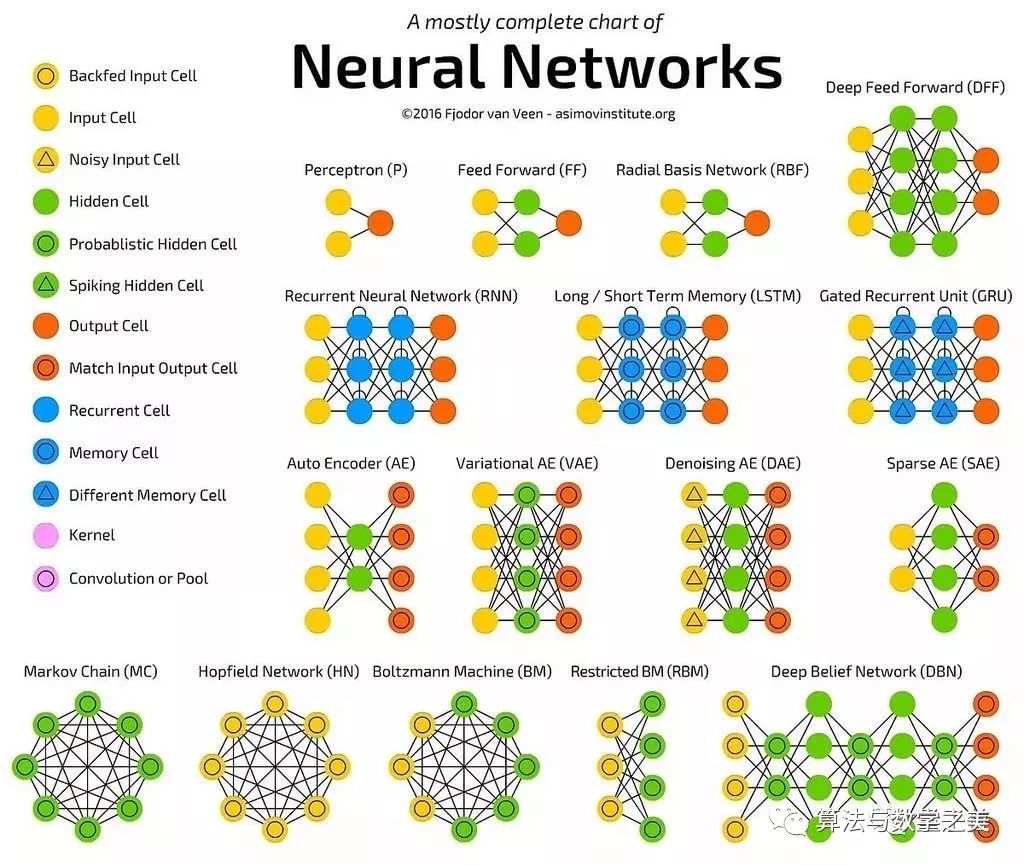
神经网络是一种机器学习模型，它们受到人类大脑中神经元结构的极大启发。 神经网络模型使用一系列激活单元（称为神经元）来预测某些结果。 神经元将输入应用于转换函数，并返回输出。

神经网络擅长获取数据中的非线性关系，并帮助我们完成音频和图像处理等任务。 虽然存在许多不同类型的神经网络（比如卷积神经网络、前馈神经网络、递归神经网络等），但它们都依赖于转换输入生成输出的基本概念。

在上图中，线条将每个圆圈连接到另一个圆圈。 在数学中，这就是所谓的图，一种由边连接的节点组成的数据结构。

神经网络的核心是一个系统，它接收数据，进行线性代数运算，然后输出答案。

线性代数是理解神经网络的关键，它通过矩阵和向量空间来表示线性方程。 因为线性代数涉及矩阵表示线性方程，所以矩阵是理解神经网络核心部分必须知道的基本知识。

矩阵是由数字、符号或表达式组成的矩形阵列，按行和列排列。 例如：

它被称为3×3矩阵，因为它有三行三列。

神经网络，每个特征都表示为输入神经元。 每个特征的数值乘以神经元的权重向量获得输出。 在数学上，该过程是这样的：

其中X是一个m×n矩阵，m是神经元输入的数量，n神经元输出的数量。 a是权重向量，aT是a的转置，b是偏置。

偏置（bias）通过向左或向右移动S形函数来影响神经网络输出，以便对某些数据集进行更好的预测。 转置（Transpose）是一个线性代数术语，它的意思是把矩阵的行变成列、列变成行。

在所有特征列和权重相乘之后，调用激活函数来确定神经元是否被激活。 激活函数有三种主要类型： RELU函数，sigmoid函数和双曲正切函数。

sigmoid函数我们已经知道了。 RELU函数是一个简洁的函数，当输入x大于0的时候输出x，当输入x小于0的时候输出0。 双曲正切函数与sigmoid函数类似，只是它用来约束-1和1之间的数值。

需要的数学知识：

离散数学和线性代数课程是必须的。 为了深入理解，还需要学习图论、矩阵论、多元微积分和实分析课程。

K-平均聚类

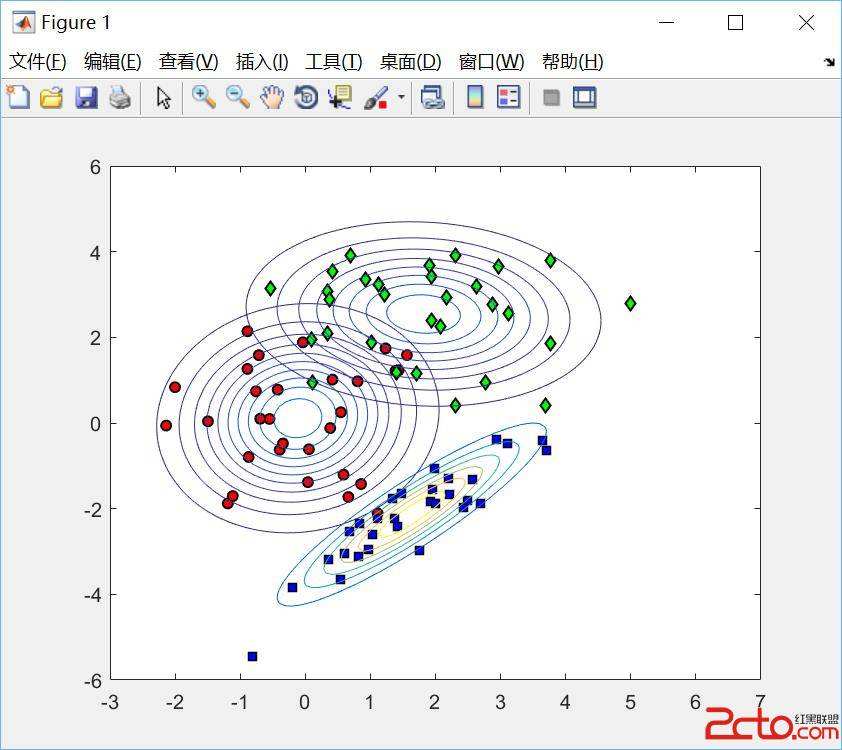
K-平均聚类（K-Means Clustering）算法是一种无监督机器学习，用于对未标记数据进行分类。 该算法通过在数据中查找组来工作，其中组由变量k表示。 它根据提供的特征将每个数据点分配给k组中的一个。

K-平均聚类依赖于整个算法中的距离概念，将数据点“分配”到聚类。 在数学中，描述集合中任意两个元素之间距离的指标有两种： 欧几里德距离和出租车距离（又叫曼哈顿距离）。

其中，(x1, y1)、(x2, y2 )是笛卡尔平面上的坐标点。

虽然欧几里得距离标准已经足够，但在某些情况下它不起作用。 假设在城市街道上乘坐出租车，那么你是没法走斜线的，只能走横平竖直的街道，这时候我们可以使用出租车距离：

需要的数学知识：

这部分牵涉到的知识比较少。 实际上你只需要知道加法和减法和代数的基础知识，就可以掌握距离公式。 但是为了深入理解每种距离的基本几何形状，建议学习欧氏几何和非欧几何。 为了深入理解指标和度量空间的含义，我会阅读数学分析并参加实分析课程。

决策树

决策树是一种类似流程图的树结构，它使用分支方法来说明决策的每个可能结果。 树中的每个节点代表对特定变量的测试，每个分支都是该测试的结果。

决策树依赖于信息论（information theory）。 在信息论中，人们对某个主题了解越多，可以知道的新信息就越少。 信息论的关键之一是熵（entropy）。 熵是变量不确定性的一种度量，具体形式为：

在上面的公式中，P(x)是数据集中特征出现的概率。 b是对数函数的底，它常见的值有2、e和10。 前面的Σ符号表示求和，它的上下方分别写着求和的上限和下限。

在计算熵之后，我们可以通过信息增益（information gain）构造决策树，它告诉哪种拆分方式会最大程度地减少熵。 信息增益的公式如下：

信息增益用于衡量可以获得多少“信息”。 在决策树中，我们可以计算数据集中每一列的信息增益，找到哪一列能为我们提供最大的信息增益，然后在该列上进行拆分。

需要的数学知识：

基本的代数和概率知识是了解决策树所必须的。

原文地址：
https://www.dataquest.io/blog/math-in-data-science/

————

编辑 ∑Gemini

 来源：新浪专栏·创事记

☞泰勒定理的奇闻轶事

☞丘成桐：漫谈微分几何

☞Leibniz 如何想出微积分？（一）

☞线性相关和秩的物理意义

☞数学史上你认为最丑陋的公式是什么？

☞陶哲轩谈什么是好的数学

☞田渊栋：数学的用处（下篇）

☞你绝对没想过原来数学家这么流氓，一言不合就进行暴力证明

☞世界上最牛的五篇博士论文

☞数学中有哪些巧合让人眼前一亮？

☞算法立功！清华毕业教授美国被抢车，警察无能为力自己用“贪心算法”找回

☞学术史上的奇文：怎样用数学抓狮子

☞台大教授的反思：最难的一课 我们却没教给学生

☞麻省理工学院(MIT)研究生学习指导—— 怎样做研究生

☞分享 数学，常识和运气 ——投资大师詹姆斯·西蒙斯2010年在MIT的讲座

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域，经采用我们将奉上稿酬。

投稿邮箱：math_alg@163.com