数据科学家需要了解的5种聚类算法
编者按:聚类是一种涉及数据点分组的机器学习技术。给定一组数据点,我们可以使用聚类算法将每个数据点到分类到图像中的特定组中。理论上,同一组中的数据点应具有相似的属性和特征,而不同组中的数据点的属性和特征则应高度不同。聚类是无监督学习的一种方法,是用于多领域统计数据分析的常用技术。
在数据科学中,我们可以通过聚类分析观察使用聚类算法后这些数据点分别落入了哪个组,并从中获得一些有价值的信息。那么今天,我们就跟着机器学习工程师George Seif来看看数据科学家需要掌握的5种实用聚类算法以及它们的优缺点。
K-Means聚类
K-Means(k-平均或k-均值)可以称的上是知名度最高的一种聚类算法,它常出现在许多有关数据科学和机器学习的课程中。在代码中非常容易理解和实现!让我们来看下面这幅动图。
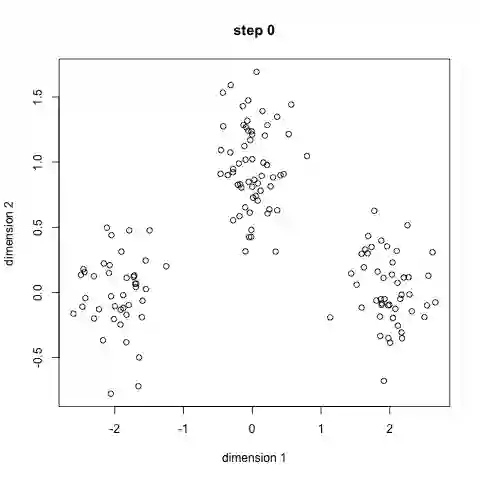
首先,我们确定要几个的聚类(cluster,也称簇),并为它们随机初始化一个各自的聚类质心点(cluster centroids),它在上图中被表示为“X”。要确定聚类的数量,我们可以先快速看一看已有的数据点,并从中分辨出一些独特的数据。
其次,我们计算每个数据点到质心的距离来进行分类,它跟哪个聚类的质心更近,它就被分类到该聚类。
需要注意的是,初始质心并不是真正的质心,质心应满足聚类里每个点到它的欧式距离平方和最小这个条件。因此根据这些被初步分类完毕的数据点,我们再重新计算每一聚类中所有向量的平均值,并确定出新的质心。
最后,重复上述步骤,进行一定次数的迭代,直到质心的位置不再发生太大变化。当然你也可以在第一步时多初始化几次,然后选取一个看起来更合理的点节约时间。
K-Means的优点是速度非常快,因为我们所做的只是计算数据点和质心点之间的距离,涉及到的计算量非常少!因此它的算法时间复杂度只有O(n)。
另一方面,K-Means有两个缺点。一是你必须一开始就决定数据集中包含多少个聚类。这个缺点并不总是微不足道的,理想情况下,我们的目标其实是用一种算法来分类这些数据,并从结果中观察出一些规律,而不是限制几个条件强行聚类。二是一开始质心点的选取是随机的,算法可能会初始化出差异巨大的点。这个缺点导致的结果是质心点的位置不可重复且缺乏一致性。
K-Medians是与K-Means相关的另一种聚类算法,不同之处在于它使用簇的中值向量来重新计算质心点。该方法对异常值不敏感(因为使用中值),但在较大数据集上运行时速度会慢很多,因为每次计算中值向量,我们都要重新排序。
Mean-Shift聚类
Mean shift算法,又称均值漂移算法,这是一种基于核密度估计的爬山算法,可用于聚类、图像分割、跟踪等。它的工作原理基于质心,这意味着它的目标是定位每个簇/类的质心,即先算出当前点的偏移均值,将该点移动到此偏移均值,然后以此为新的起始点,继续移动,直到满足最终的条件(找出最密集的区域)。如果没理解,请看下图。
Mean-Shift聚类
为了理解均值漂移,我们可以像上图一样想象二维空间中的一组数据点,然后先随机选择一个点C,以它为圆心画一个半径为r的圆开始移动。之前提到了,这是个爬山算法,它的核函数会随着迭代次数增加逐渐向高密度区域靠近。
在每轮迭代中,算法会不断计算圆心到质心的偏移均值,然后整体向质心靠近。漂移圆圈内的密度与数据点数成正比。到达质心后,算法会更新质心位置,并继续让圆圈向更高密度的区域靠近。
当圆圈到达目标质心后,它发现自己无论朝哪个方向漂移都找不到更多的数据点,这时我们就认为它已经处于最密集的区域。
这时,算法满足了最终的条件,即退出。
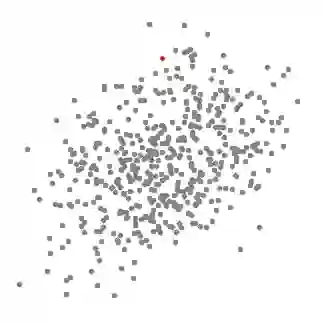
这里我们主要介绍了一个漂移圆圈的思路,如下图所示,其实Mean shift算法事实上存在多个圆形区域,图中黑点代表质心,而灰点则是数据点。
和K-Means算法相比,Mean-Shift不需要实现定义聚类数量,因为这些都可以在计算偏移均值时得出。这是一个巨大的优势。同时,算法推动聚类中心在向密度最大区域靠近的效果也非常令人满意,这一过程符合数据驱动型任务的需要,而且十分自然直观。如果要说Mean-Shift有什么缺点,那就是对高维球区域的半径r的定义,不同选择可能会产生高度不同的影响。
具有噪声的基于密度的聚类方法(DBSCAN)
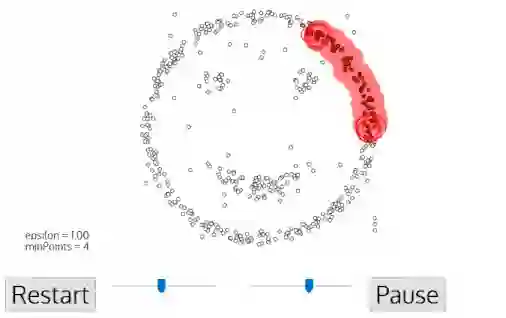
DBSCAN是一种基于密度的聚类算法,它与mean-shift类似,但又有一些显著优势。我们先来看看下面这幅花哨的图。
DBSCAN笑脸聚类
首先,DBSCAN算法会以任何尚未访问过的任意起始数据点为核心点,并对该核心点进行扩充。这时我们给定一个半径/距离ε,任何和核心点的距离小于ε的点都是它的相邻点。
如果核心点附近有足够数量的点,则开始聚类,且选中的核心点会成为该聚类的第一个点。如果附近的点不够,那算法会把它标记为噪声(之后这个噪声可能会成为簇中的一部分)。在这两种情形下,选中的点都会被标记为“已访问”。
一旦聚类开始,核心点的相邻点,或者说以该点出发的所有密度相连的数据点(注意是密度相连)会被划分进同一聚类。然后我们再把这些新点作为核心点,向周围拓展ε,并把符合条件的点继续纳入这个聚类中。
重复步骤2和3,直到附近没有可以扩充的数据点为止,即簇的ε邻域内所有点都已被标记为“已访问”。
一旦我们完成了这个集群,算法又会开始检索未访问过的点,并发现更多的聚类和噪声。一旦数据检索完毕,每个点都被标记为属于一个聚类或是噪声。
与其他聚类算法相比,DBSCAN有一些很大的优势。首先,它不需要输入要划分的聚类个数。其次,不像mean-shift,即使数据点非常不同,它也会将它们纳入聚类中,DBSCAN能将异常值识别为噪声,这就意味着它可以在需要时输入过滤噪声的参数。第三,它对聚类的形状没有偏倚,可以找到任意大小和形状的簇。
DBSCAN的主要缺点是,当聚类的密度不同时,DBSCAN的性能会不如其他算法。这是因为当密度变化时,用于识别邻近点的距离阈值ε和核心点的设置会随着聚类发生变化。而这在高维数据中会特别明显,因为届时我们会很难估计ε。
EM聚类
均值→质心,方差→椭圆聚类,权重→聚类大小。
K-Means算法的主要缺点之一是它直接用了距离质心的平均值。我们可以从下图中看出这样做为什么不好——图的左侧是两个半径不同的同心圆,K-Means没法处理这个问题,因为这些聚类的平均值非常接近;图的右侧是一个中心对称的非圆形分布,K-Means同样解决不了它,因为如果单纯依靠均值判断,算法无法捕捉更多特征。
高斯混合模型(GMM)比K-Means算法具有更好的灵活性。它是多个高斯分布函数的线性组合,理论上可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况。对于GMM,我们假设数据点满足不同参数下的高斯分布——比起均值,这是一个限制较少的假设。我们用两个参数来描述聚类的形状:均值和标准差!以二维分布为例,标准差的存在允许聚类的形状可以是任何种类的椭圆形。因此这个算法的思想是:如果数据点符合某个高斯分布,那它就会被归类为那个聚类。
为了找到每个聚类的高斯参数,我们要用到一种名为期望最大化(EM)的优化算法。下图是高斯混合模型的聚类过程,那么,你知道怎么在其中运用EM算法吗?
首先,我们确定聚类的数量(如K-Means),并随机初始化每个聚类的高斯分布参数。你也可以尝试通过快速查看数据来为初始参数提供更好的猜测,但从上图可以看出,这其实不是很必要,因为算法会很快进行优化。
其次,根据每个聚类的高斯分布,计算数据点属于特定聚类的概率。如果数据点越接近高斯质心,那它属于该聚类的概率就越高。这很直观,因为对于高斯分布,我们一般假设大部分数据更靠近聚类质心。
在这些概率的基础上,我们为高斯分布计算一组新的参数,使聚类内数据点的概率最大化。我们用数据点位置的加权和来计算这些新参数,其中权重就是数据点属于聚类的概率。为了可视化这个过程,我们可以看看上面的图片,特别是黄色的聚类。第一次迭代中,它是随机的,大多数黄点都集中在该聚类的右侧。当我们按概率计算加权和后,虽然聚类的中部出现一些点,但右侧的比重依然很高。随着迭代次数增加,黄点在聚类中的位置也完成了“右下→左下”的移动。因此,标准差的变化调整着聚类的形状,以使它能更适合数据点的分布。
迭代步骤2和步骤3,直至收敛。
论智注:对于上述第3步,请结合混合高斯模型定义公式理解。如果我们设K为模型的个数,πk为第k个高斯的权重,即第k个高斯的概率密度函数,其均值为μk,方差为σk。我们对此概率密度的估计就是要求πk、μk和σk各个变量。当求出的表达式后,求和式的各项的结果就分别代表样本x属于各个类的概率。在做参数估计的时候,常采用的方法是最大似然。——引自 姜文晖《聚类(1)——混合高斯模型》
GMM有两个关键优势。首先它比K-Means更灵活,由于标准差的引入,最后聚类的形状不再局限于圆形,它还可以是大小形状不一的椭圆形——K均值实际上是GMM的一个特例,其中每个聚类的协方差在所有维上都接近0。其次,权重的引入为同一点属于多个聚类找到了解决方案。如果一个数据点位于两个聚类的重叠区域,那我们就可以简单为它定义一个聚类,或者计算它属于X聚类的百分比是多少,属于Y聚类的百分比是多少。简而言之,GMM支持混合“成员”。
谈及缺点,和K-Means相比,GMM每一步迭代的计算量比较大。另外,它的求解办法基于EM算法,因此有可能陷入局部极值,需要经过多次迭代。
层次聚类
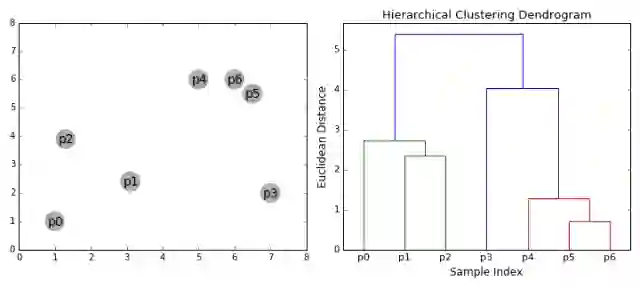
层次聚类实际上可以被分为两类:自上而下和自下而上。其中自下而上算法(Bottom-up algorithms)首先会将每个数据点视为单个聚类,然后连续合并(或聚合)成对的聚类,直到所有聚类合并成包含所有数据点的单个聚类。它也因此会被称为hierarchical agglomerative clustering 或HAC。该算法的聚类可以被表示为一幅树状图,树根是最后收纳所有数据点的单个聚类,而树叶则是只包含一个样本的聚类。在讲解具体步骤前,我们先看看整个过程的图解。
层次聚类
首先,我们把每个数据点看作是一个聚类,即如果数据集中有X个数据点,它就有X个聚类。然后我们设置一个阈值作为衡量两个聚类间距离的指标:如果距离小于阈值,则合并;如果距离大于阈值,迭代终止。
在每轮迭代中,我们会把两个聚类合并成一个聚类。这里我们可以用到average linkage,它的思路是计算所有分属于两个目标聚类的数据点之间距离,然后求一个平均值。每次我们会根据设定的阈值选取平均距离最小的两个聚类,然后把它们合并起来,因为按照我们的标准,它们是最相似的。
重复步骤2,直到我们到达树根,即最后只有一个包含所有数据点的聚类。通过这种方式,我们可以选择要几个聚类,以及什么时候停止聚类。
层次聚类不要求我们指定聚类的数量,由于这是一个构建树的过程,我们甚至可以选择那种聚类看起来更合适。另外,该算法对距离阈值的选择不敏感,无论怎么定,算法始终会倾向于给出更好地聚类结果,而不像其他算法很依赖参数。根据层次聚类的特点,我们可以看出它非常适合具有层次结构的数据,尤其是当你的目标是为数据恢复层次时。这一点是其他算法无法做到的。与K-Means和GMM的线性复杂性不同,层次聚类的优势是以较低的效率为代价,因为它具有O(n3)的时间复杂度。
结论
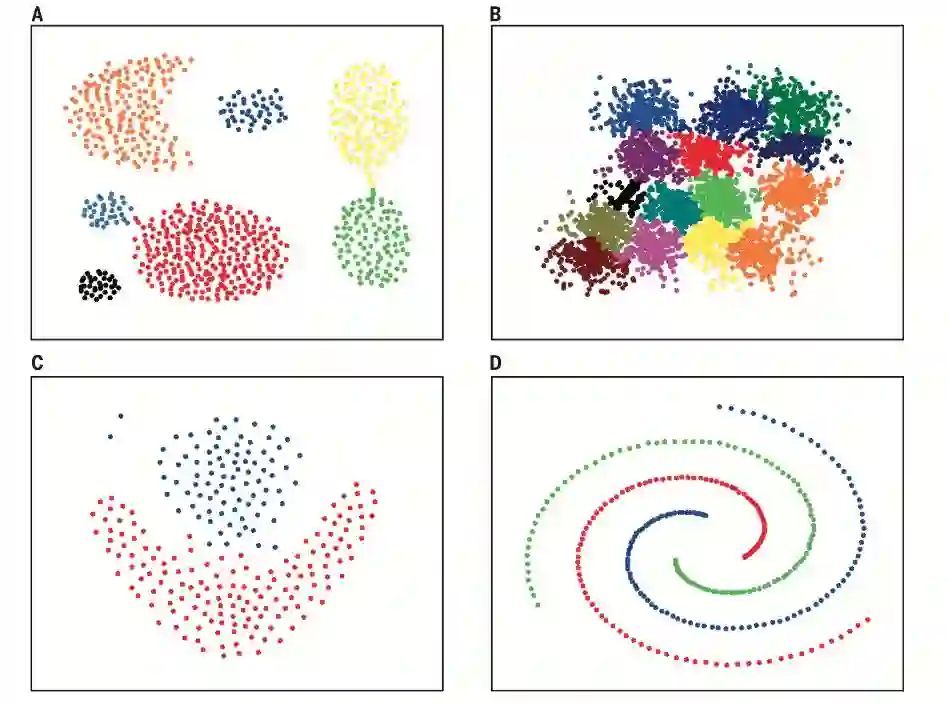
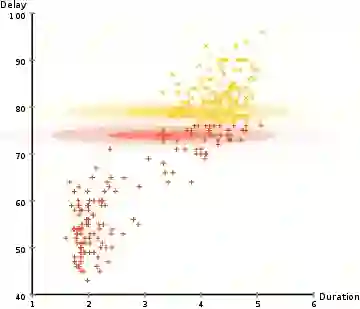
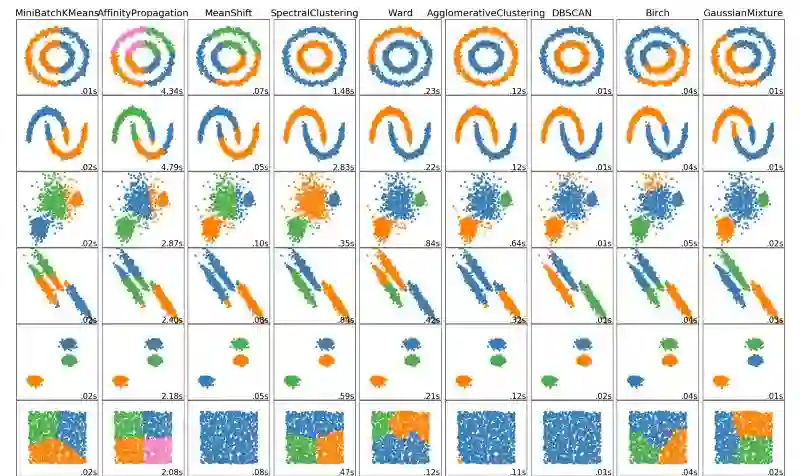
以上就是数据科学家需要知道的5个聚类方法。在文章的最后,就让我们以一幅聚类图做结,直观展示这些算法和其他算法的完美表现!
原文地址:towardsdatascience.com/the-5-clustering-algorithms-data-scientists-need-to-know-a36d136ef68