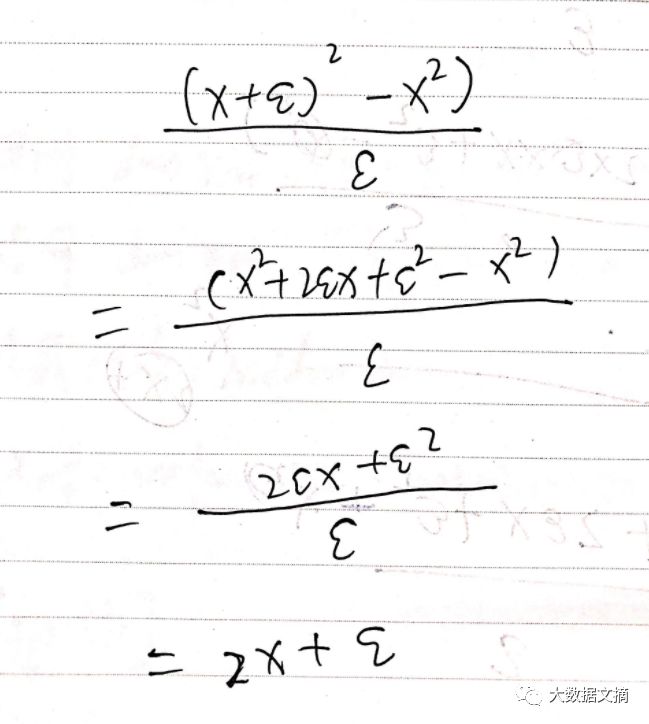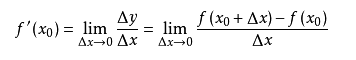学界 | Ian Goodfellow推特小课堂又开课啦：数学求导的小技巧

大数据文摘作品

作者：小鱼、蒋宝尚

最近，Ian Goodfellow不断在推特和大家分享一写学习的小技巧。在昨天和大家分享了推导机器学习公式推导的黑魔法后，今天又连发几条推特，和大家分享了数学中求导数的小技巧。

Goodfellow称，他最喜欢用超实数（hyperreal numbers）来求导数。

注：超实数是一个包含实数以及无穷大和无穷小的域，它们的绝对值分别大于和小于任何正实数。

以下是Ian Goodfellow推特内容：

对于这个技巧，我们介绍一种新的数字，称为无穷小超实数。假设我们有一个无穷小量ε，而且其取值范围是0<ε<x，其中x是指所有正实数。并假设我们可以用代数表示任意像ε这样的变量。

现在我们可以通过套用这个表达式：f'(x)= real_part(f(x + ε) - f(x)) / ε)，使用代数方法来计算导数，其中“real_part”函数的功能是四舍五入某些表达式的无穷小量。

例如，x^2的导数为：((x + ε)^2 - x^2) / ε = (x^2 + 2*ε*x + ε^2 - x^2) / ε = 2 + ε。我们舍去无穷小量ε，而只保留2。

看到这里，趁着小编的高数还没有忘干净，就忍不住拿起笔来推导了一下x^2的导数：

字丑请忽略……

嗯……，结果怎么不一样呢？这不是最基本的求导公式嘛！

经过再三确认，原来是Goodfellow在结果中漏写了一个x，x^2的导数为：((x + ε)^2 - x^2) / ε = (x^2 + 2*ε*x + ε^2 - x^2) / ε = 2*x + ε。我们舍去无穷小量ε，而只保留2x。

看到这里，不少读者朋友会吐槽，这不是就高数里面求导法则的定义嘛！没错，让我们一起来温习一下高数：

可以说，Goodfellow的小技巧确实和求导法则的定义很相似，但是求导法则前面有一个很叫lim的东东，称当Δx→0时，极限存在。

要证明Δx→0时极限存在，那可就是一件数学上的很有讲究的事了，当然理解起来也并不容易。

那么Goodfellow的技巧高明在哪里？答案就是通过定义一个无穷小量来取代求极限这一步骤。

Goodfellow也称，用无穷小的超实数进行代数运算，就像一场骗局。但事实证明，当对实数有相同的规则时，那么代数的运算法则在逻辑上就是可行的。

超实数把牛顿和莱布尼茨在微积分早期发展过程中凭直觉感知到的知识更加具体化，但并没有严格的数学证明。超实数比极限的概念更接近无穷小域的本质。

也存在无穷大的超实数，即比任何实数都大的数，但Goodfellow并不认为其在机器学习研究中能够发挥很大的作用。

也可以用超实数计算积分，但在推导过程中我并没有发现超实数在计算积分方面具有很大的优势。

相关报道：

https://twitter.com/goodfellow_ian/status/996559213500424192

【今日机器学习概念】

Have a Great Definition