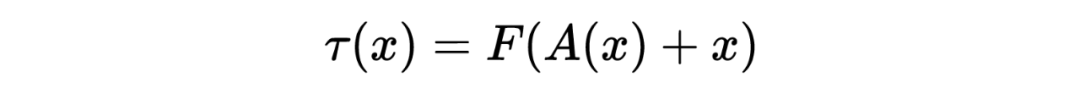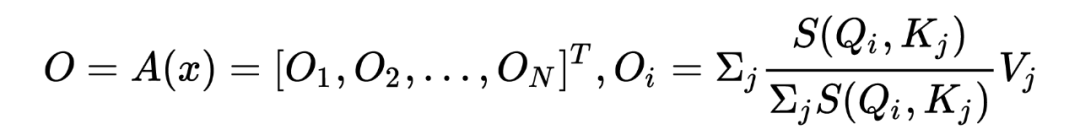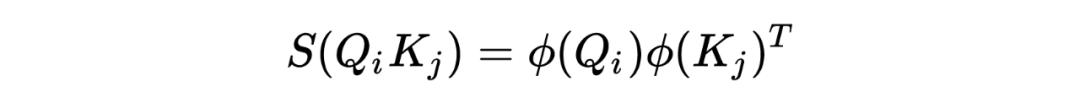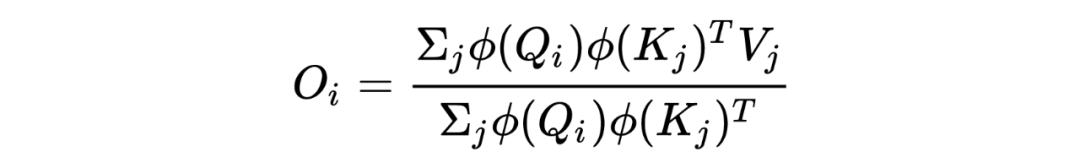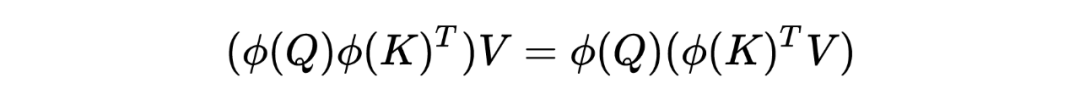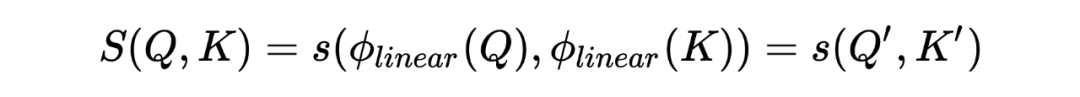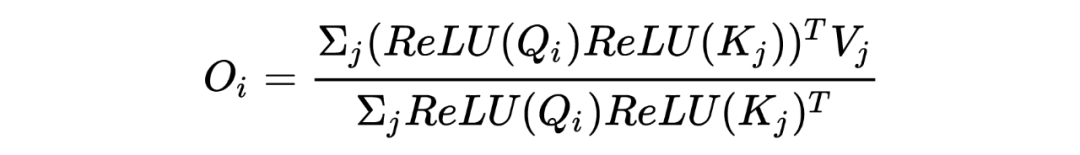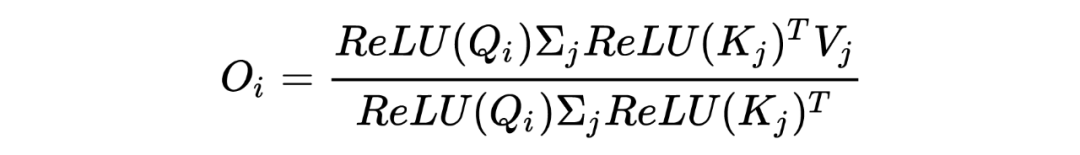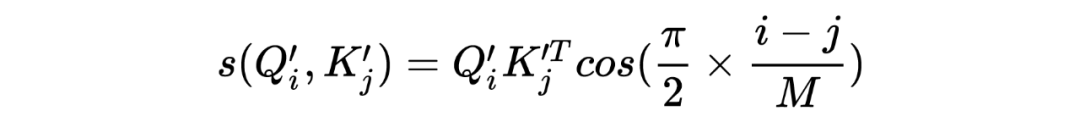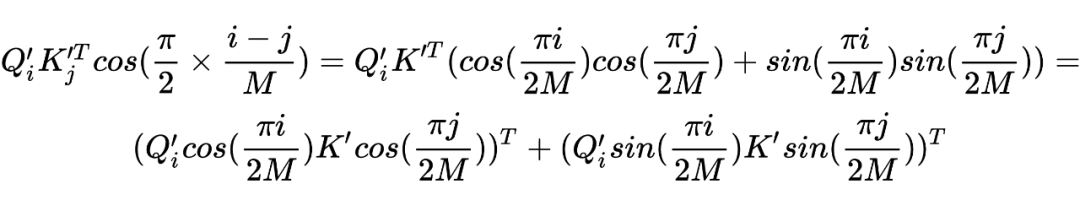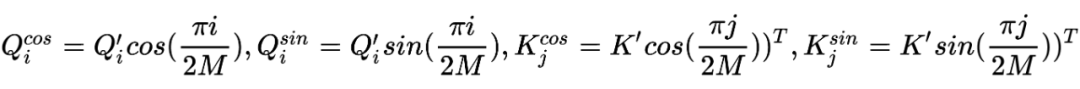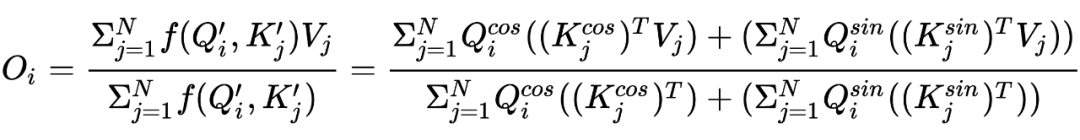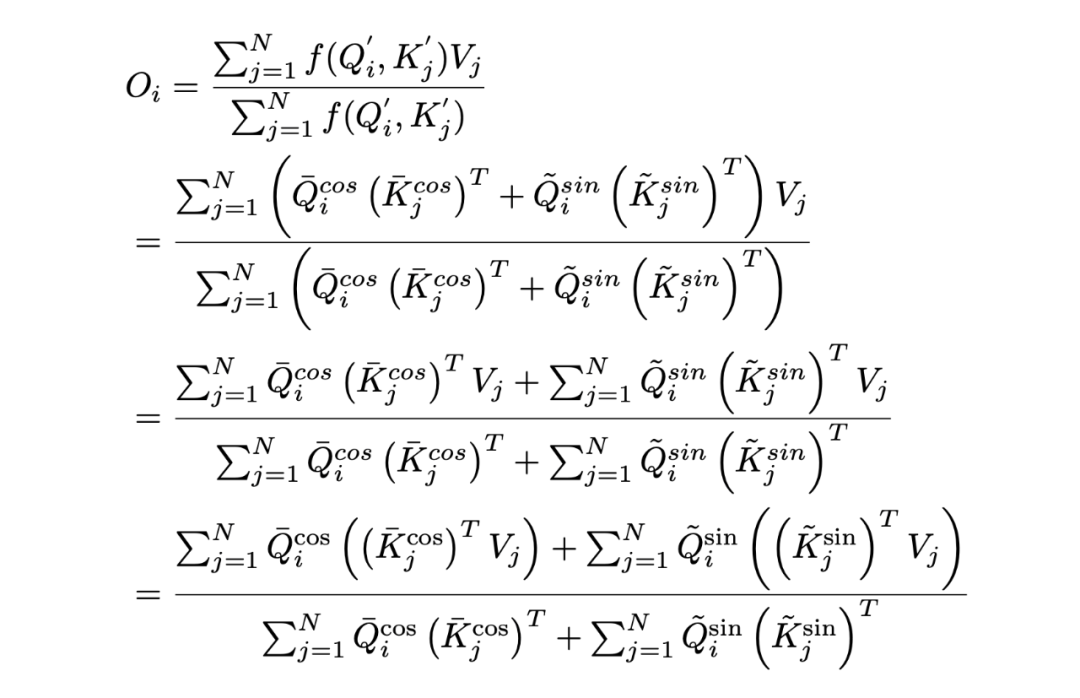ICLR 2022 | 在注意力中重新思考Softmax，商汤提出cosFormer实现多项SOTA

©作者 | 李文

单位 | 中南大学

研究方向 | 自然语言处理

最近读了一篇 ICLR 2022 的论文，对于 attention-softmax 的计算复杂度有了一定的了解，下面是对论文的翻译和笔记，如有理解错误，还请海涵指正。

论文标题：

cosFormer: Rethinking Softmax in Attention

论文链接：

https://arxiv.org/pdf/2202.08791.pdf

代码链接：

https://github.com/OpenNLPLab/cosFormer

摘要

Transformer 在自然语言处理、计算机视觉和音频处理，已经取得了巨大的成功。作为核心组件的 attention-softmax，可以有效捕捉长距离的特征，但是计算复杂度是序列长度的平方；核方法的提出就是为了减少其计算的时间复杂度，但是这是一个近似方法，受语料和任务场景影响，并且有一定的误差。

这篇论文提出 cosformer 的一种方法，媲美标准 attention 甚效果更好。COFORMER 基于两个关键 softmax注意力的属性，第一个：注意矩阵的非负性， 第二个：非线性的权重转换（re-weighting）方案，放大局部的注意力权重值。

INTRODUCTION

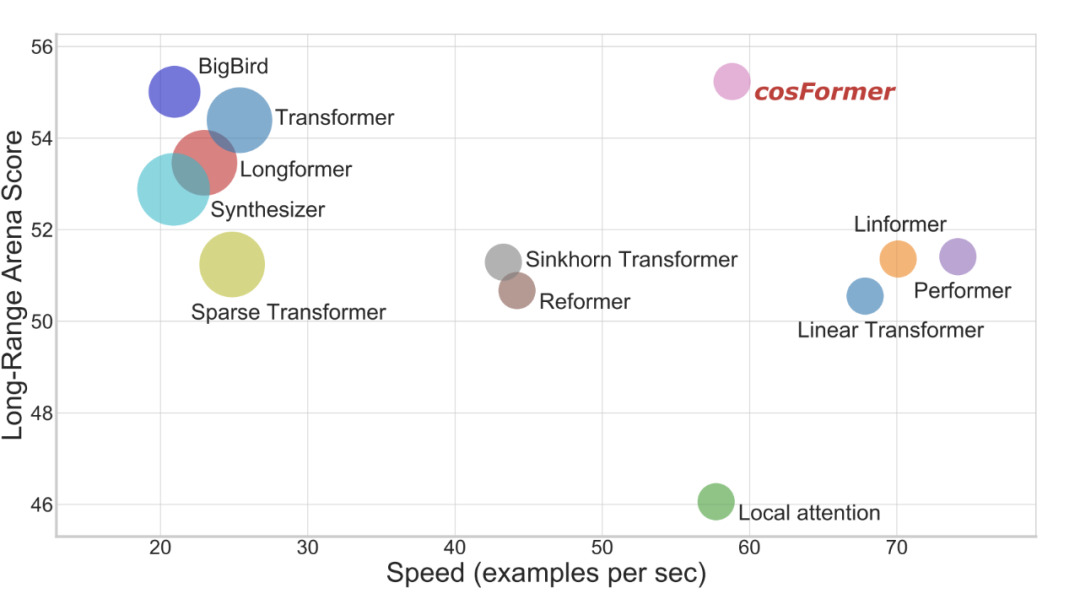
Figure 1：上图中，y 轴表示性能，x 轴表示计算速度，圆圈的大小表示显存占用，可以看到 cosFormer 在保持长距离任务下，与左上角的任务相比：不仅保持了性能，提升了计算速度，显存占用也减少了。

transformer 及其变体在过去几年对文本、音视频任务产生了很大的影响，相较于 cnn 和 rnn，这一类模型可以学习长度不一的数据集，适用范围更大，并且有利于捕捉其全局信息，刷爆了多个任务。点乘的 attention+softmax 机制是其捕捉长距离任务的关键，遗憾的是，其空间和时间复杂度，受到了序列长度的限制，尤其是在长距离任务下影响比较明显一些。

为了解决这个问题，多种方法被提出，比如，2020 年提出的稀疏 attention 矩阵，低秩表达，核方法等等，这些方法都是为了解决标准 attention 的计算复杂度。然而这些线性时间复杂下的变体，通常存在一定的假设前提，并且是一个近似值，自带约束，换句话说，这些方法可能并不能适应所有场景，尤其是在 GLUE benchmark 上，通常效果没有标准（香草）的 attention 要好。另外不适用于 AR 语言模型的的 causal attention 注意力，也不适用 Linformer 和 BigBird 的交叉注意力。

softmax 是优化复杂度的主要难点所在（如果没有 softmax，利用矩阵的乘法结合律（AB）C=A（BC），可以看下面的图），我们（下文都指：作者们认为）很那去逼近它，因此作者提出疑问：“我们要得到一个关键的权重信息时，能否适用一个线性方法去替代 softmax”，这样既保留了 attention 的关键特性，又可以利用结合律，先算 KV，通过深入挖掘。

我们找到了两个关键信息：1、attention 中的权重元素是非负的，2：将权重进行 re-weigthing 的转化是为了模型的稳定性，比如，（Katharopoulos et al., 2020）提出的线性 Transformer 使用了 的指数激活函数，来保证 Q、K 非负（这样乘出来的 A 注意力矩阵也是非负的）， 然而，由于缺少一个 softmax 去 re-weigthing 权重, 模型表现不尽人意。

这篇 paper 中，我们提出了一个新的线性 Transformer 变体，命名为“COSFORMER”，满足上面的两个性质，在计算内积之前，我们先使用 relu 进行激活，强制将 K、Q 变成非负；另外我们使用了一个新的方法 将 K、Q 得到的 A 矩阵进行缩放 re-weigthing，来保障稳定性。这可以帮助模型关注局部上下文信息，通常局部上下文在 NLP 任务中比较重要。

由于 Ptolemy 定理的存在，attention 的计算可以分解，让计算可以变成线性复杂度（先算 K、V），我们使用了 AR 和 AE 模型预训练模型，在很多任务上进行了实验，结果显示 cosformer 使用更小的显存，更快的速度就可以媲美标准的 Attention。并且刷新了 Long-Range Arena benchmark。

OUR METHOD

这一节主要讲 COSFORMER 详细的技术实现，最关键的点就是如何替换掉标准 Attention 中，非线性的并且不可拆分的 softmax 函数，使用一个非线性的可以拆分成线性操作进行替换；我们的方法适用范围比较广，causal 和 cross attentions 都支持，并且是线性的时间空间复杂度（说的都是跟输入序列长度 N 成线性），在长文本上表现较好。

标准Attention

标准的 Attention 通常是给定一个输入长度为  的序列 ，然后通过  embedding 层表示为 的矩阵形式，然后经过一个 encoder 的 self-attention 模块 ： ，公式如下：

其中 F 是一个包含残差的前向连接，A 表示的是 attention 计算结果，A 的计算时间和空间复杂度为 ，所以对于长文本而言，这个公式就会存在一个瓶颈。 中有三个重要的权重 ，用于计 、 、 ，，这里使用 表示一个矩阵的第 行，用 来表示 A 函数的输出，那么有如下公式成立：

其中 表示的是一个 token 的向量，来自于多个 的加权和， 表示点乘，可以理解为相似度，计算每一个 的时间复杂度为 O（N），这里就可以看到时间复杂度与输入序列长度 成平方关系。如果 ，就是 softmax 了。

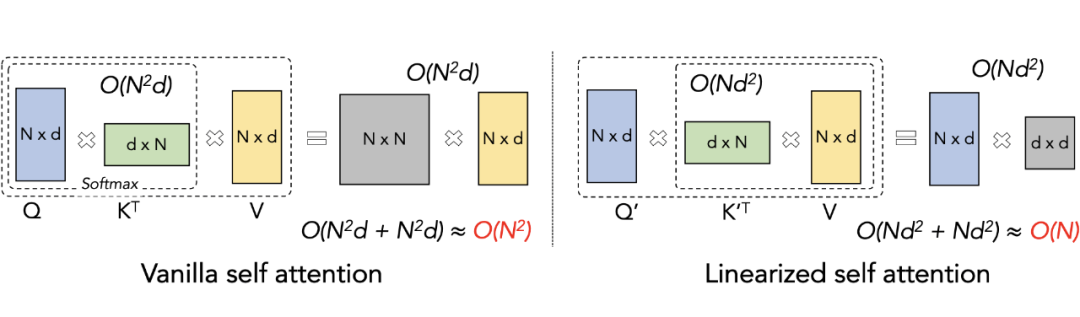
线性复杂度的self-attention

根据上面的公式，我们可以使用一个相似的方法，去计算 attention 矩阵，我们的目的是希望， 、 的计算式可以拆分的成线性的，而不是跟 softmax 一样不可拆分，所以对 进行如下表示：

其中 是将 和 映射到另外一个隐空间,我们重写上一节的公式得到了：

因为矩阵乘法的结合律，我们就可以得到如下公式是成立的：

这样就解决了计算复杂度的问题，可以参见下面的图：

上图已经很明显的标出了其复杂度，当 ，时间复杂度与输入序列长度的关系显而易见。那么之前的解法有哪些呢，综上所以，核心点是寻找一个可以拆分的 方法，一种方法是希望找到 softmax 的一个近似值，比如 RFA 和 Performer。

另外一种是进行替换，比如 linear transformer 直接替换了 softmax，先使用 将 、 的分量变成非负的，然后直接 得到非负的 Attention 矩阵。但是在我们的实验中，我们发现这种方法对于长距离任务而言，效果并不好（见上图），本论文也是提出了另外的方法替换 softmax 实现了更好的性能。

softmax attention的分析

在标准的 self-attention 中， ，实际上是在 矩阵的行上面做了一个 re-weighting，换句话说，是对一个 token 和其他 token 的关联关系权重做了一个 re-weighting，然而抛开之前的论文和经验，softmax-attention 的关键和必要特征是什么呢？（作者的意思应该是，这里要抛开之前的解释，只谈这个矩阵的特征，我对这句话的理解是深度学习本身也不需要解释，即使解释不了，也可以拟合得到好的效果，欢迎指正）。

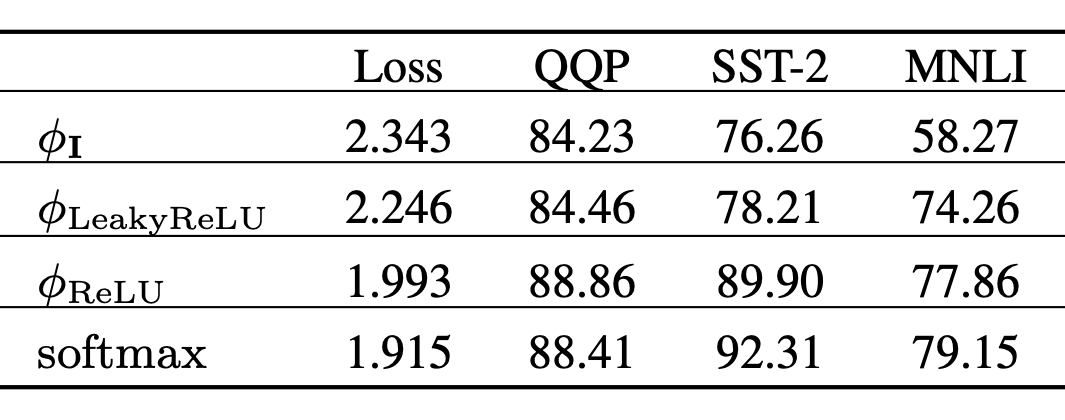
这里很容易得到两个重要的特征，1、 矩阵是非负的 2、提供了一个非线性的 re-weighting 机制，拟合权重的分布，增加训练稳定性。为了验证上面的猜想，设计了一些实验，实验结果在下面表格中。

上图中 表示对 、 都乘以单位阵，值没有任何变化， 对 、 激活后负数会变小，正数不变。 对 、 进行激活，这样所有分量就非负了， 表示标准的 attention 权重计算，上面的实验是依次增加我们总结的关键点。

首先验证非负的的重要性，上图中 表示单位阵，即不对输入进行任何转化，对比 和其他中实验的结果可以看到非负是比较重要额，其次验证 re-weighting 的重要性，其中 softmax 是唯一进行了 re-weighting 的，同其他三个进行比较也可以看到其区别。

对比 和 可以看到，softmax 可以让模型更快收敛，对于很多下游任务更好（图里面有两个都更好一些），这可能是因为 softmax 会放大数值，模型会更加关注一些敏感的模式。

COSFORMR

针对之前的观察，我们提出了 COSFORMER，保留了 Attention 矩阵的非负性和 re-weighting 权重。COSFORMER 包含了两个重要的模块：线性的映射核函数 ，用于保证非负性；cos-Based re-weighting 机制，线性核函数 呼应了最开始的 ，定义如下：

负责将 映射到 ， 是一个可以拆分的的相似度计算方法。本文定义了 ，一方面保证 非负，另外又是非线性的转换。因此我们可以得到 的表示如下：

，继续进行变换得到下面的等式：

这样子就已经让时间复杂度降下来了，换句话说就是本来标准的 self-Attention： = [（向量·向量=标量）]*向量 ，换成了一个 Q、K、V 三个矩阵点乘，这个满足结合律，可以交换计算的先后顺序，没懂可以看上面的图，Linear Transfomer 就是这么干的，做完这个还不够，还需要对权重进行 re-weighting，加速收敛，增强稳定性。

而 re-weighting 设计的目标也是必须可以拆分的函数，作者在设计这个函数的时候，首先分析了 softmax 起到的作用，然后构思了一个可以拆分的 cos-Based Re-weighting。

cos-Based Re-weighting Mechanism

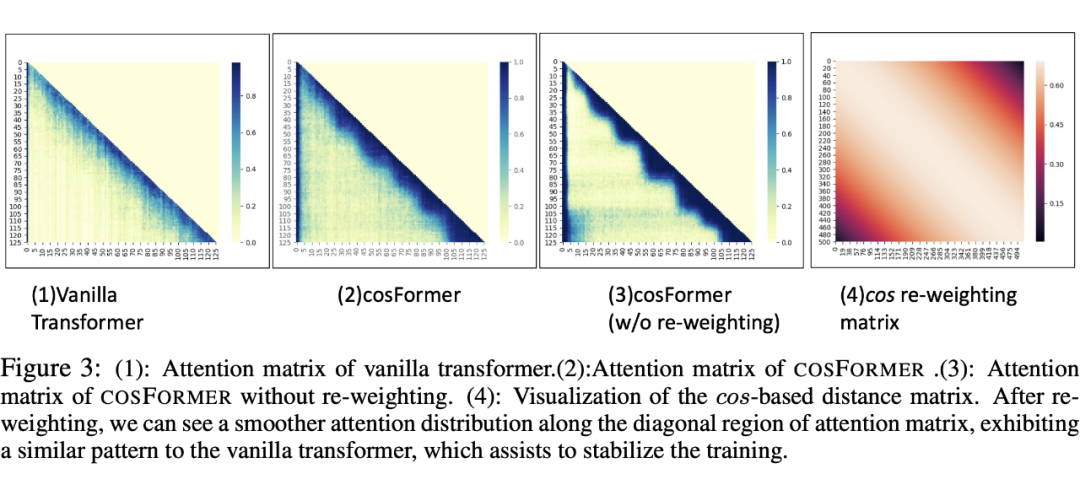
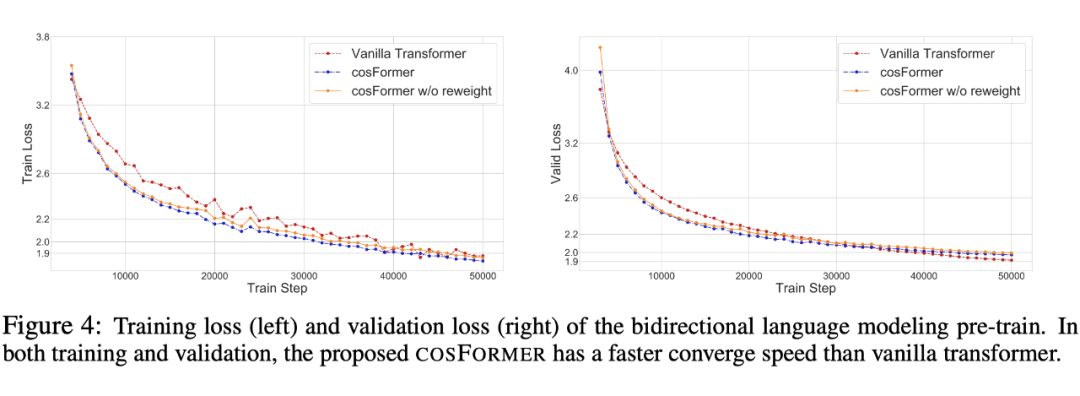
进行非线性的 re-weighting 去拟合分布，可以加速收敛，稳定训练过程。我们同样发现，由于 其收缩放大的属性，可以惩罚远距离的 token 权重，增大近距离的局部上下文权重。可以参考下面的两张图：

针对这两点，提出了 cos-Based Re-weighting 方法，

根据 Ptolemy 定理，我们可以进行拆分：

其中 表示位置， ，M 是一个超参，代码中通常用的就是 seq_length（causal attention 对应的是 query 和 key 中最长的）， 表示的就是距离,距离越远， 越大， 上面的值就小；令

, 得到下面的公式：

推导过程如下：

最终，在不损失标准 Tansformer 优势的情况下，我们的到 COSFORMER 公式如下：

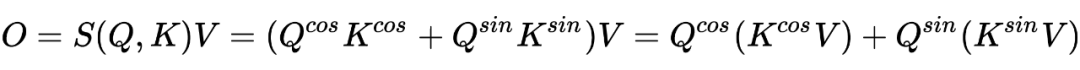
与位置编码的关系

上面的公式中，我们可以看到公式中存在 这样的位置关系，cosformer 提出了一种新的想法，可以解释为相对位置偏差。相较于 Rotary Position Embedding（2021 RoFormer），参考苏神：Transformer升级之路：博采众长的旋转式位置编码，膜拜下苏神。相较于 Stochastic Positional Encoding（2021），它是利用采样策略近似 softmax，并且使用了相对位置编码。

代码

代码作者已经实现了，自己大概看了下，长距离下对计算速度是有提升的，总结起来就是论文的第一张图。有兴趣可以自己看下，cosFormer 论文内的伪代码贴在下面了。

作者的 Pytorch 实现 Github：

https://github.com/OpenNLPLab/cosFormer

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·