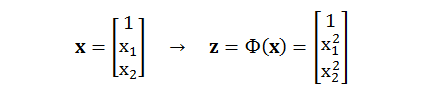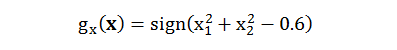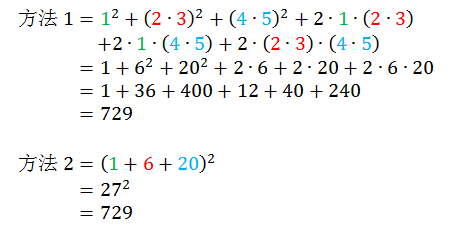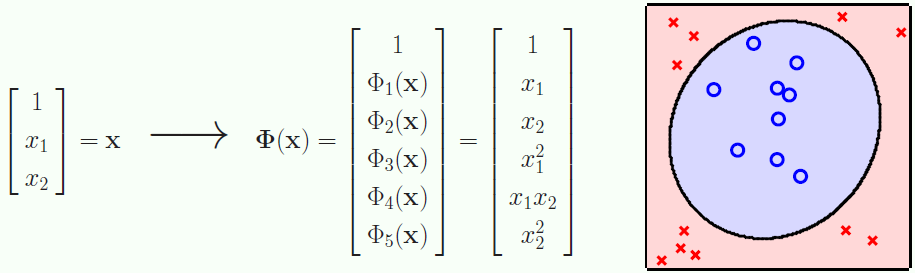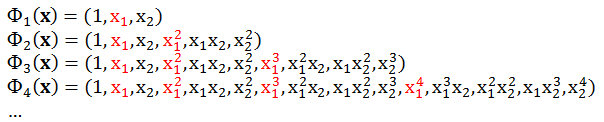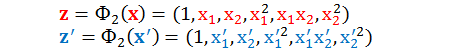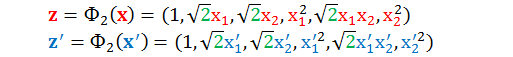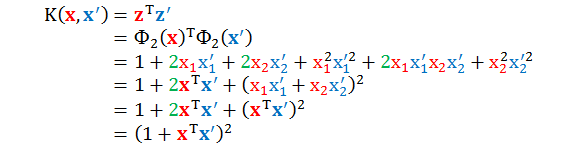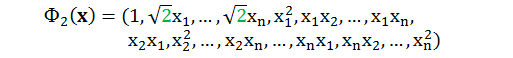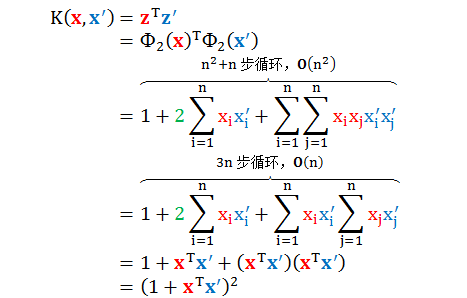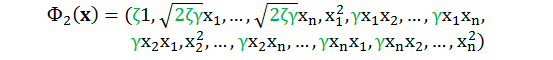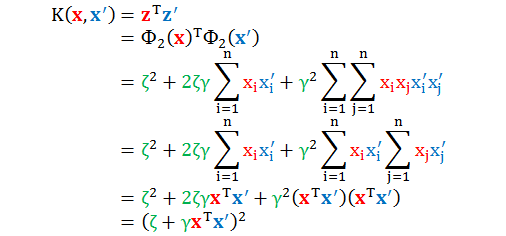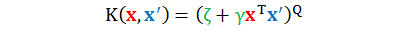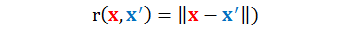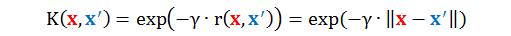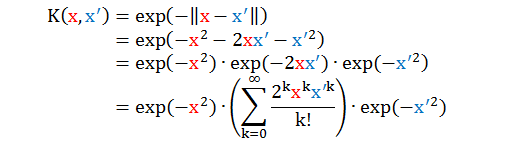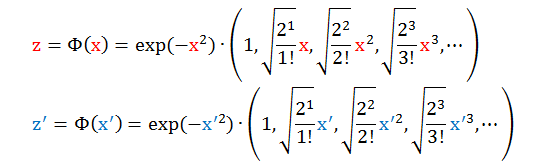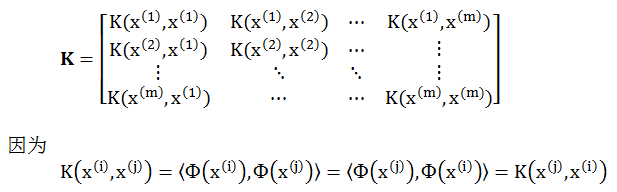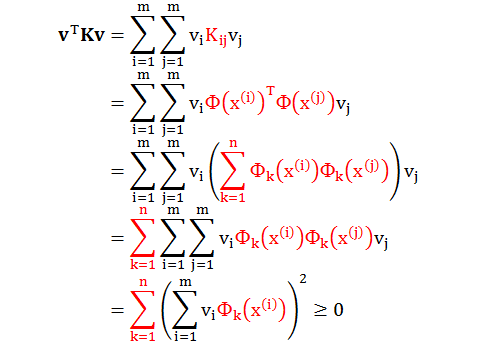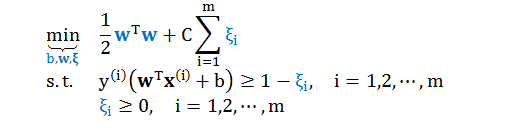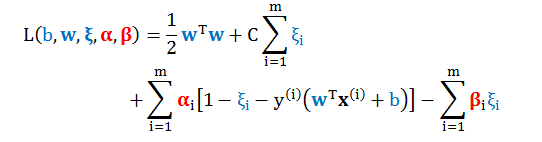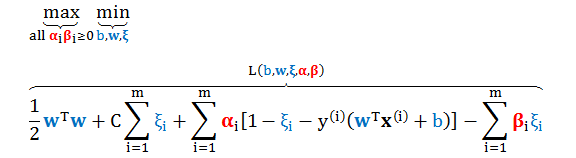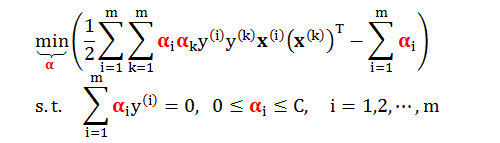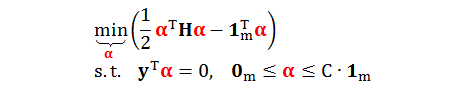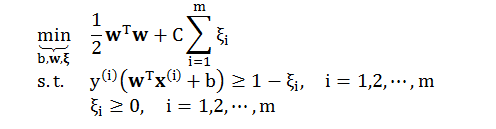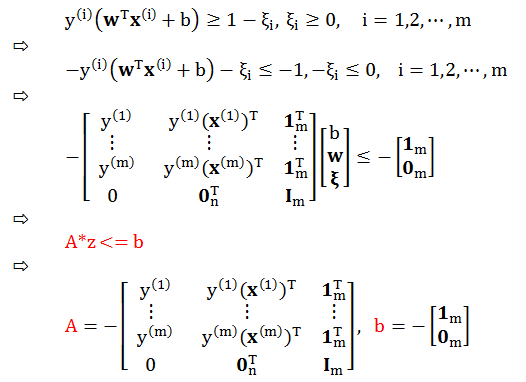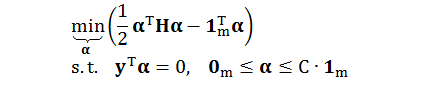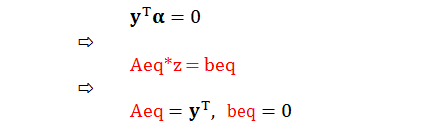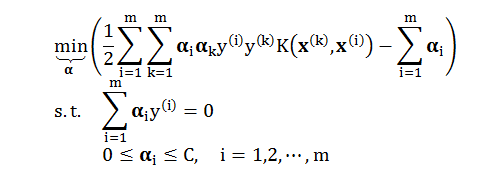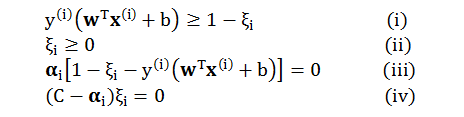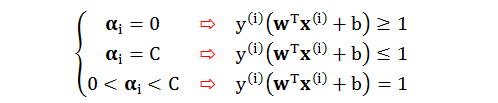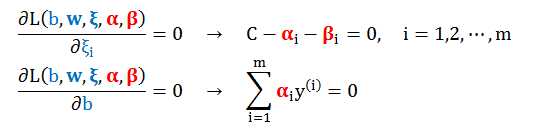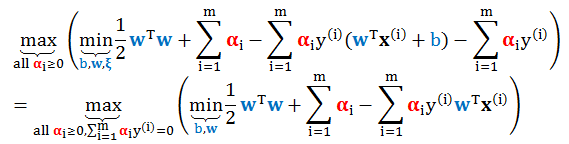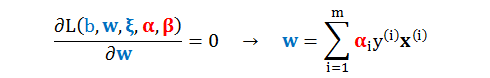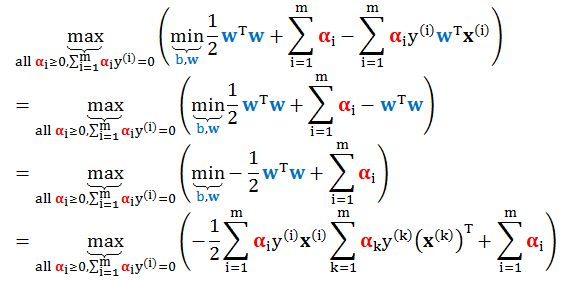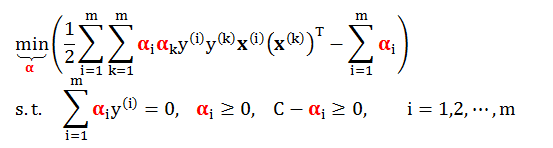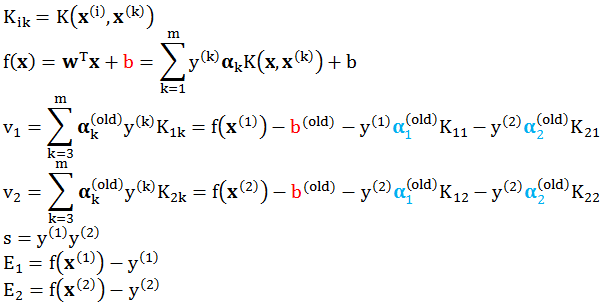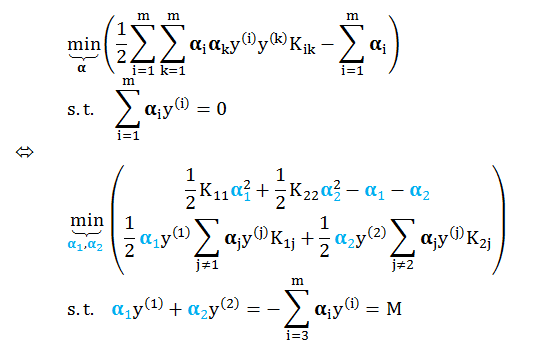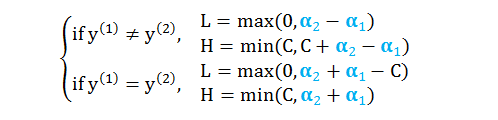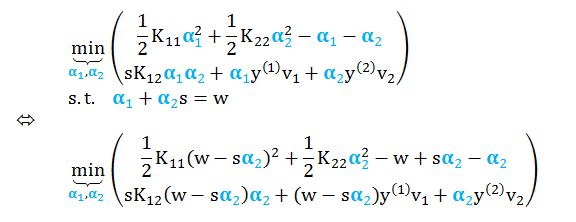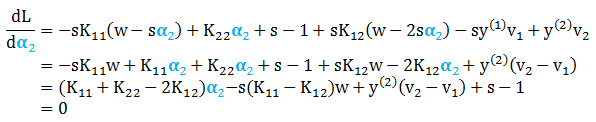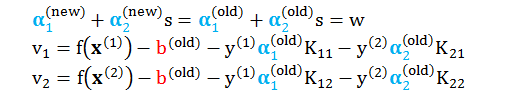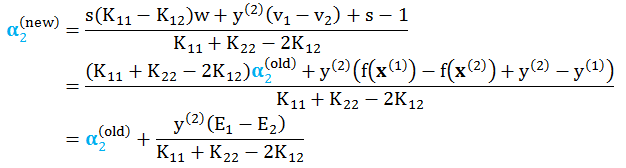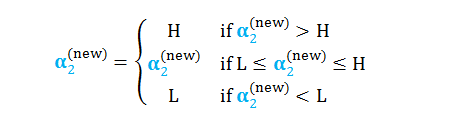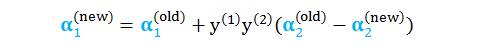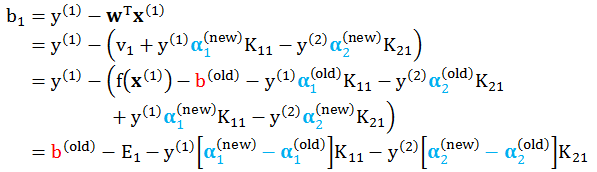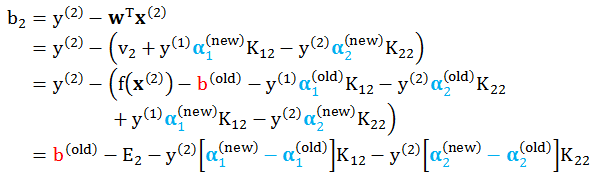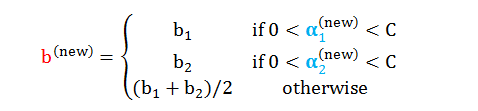支撑向量机 (下)

引言

礼貌提醒：看本贴之前建议回顾上贴支撑向量机(上) 的三个情景。上贴详细探讨了情景一的线性可分问题；而本贴要解决情景二、三的线性不可分问题。

 

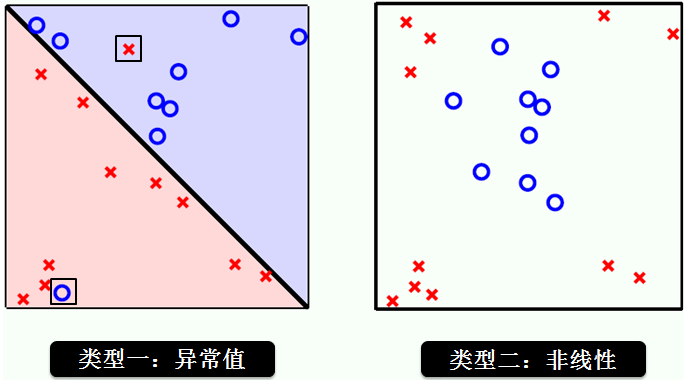
线性不可分有两种情况，按照不可分的程度来讲

• 类型 1：线性轻微不可分 (情景三)

• 类型 2：线性重度不可分(情景二)

如下图所示：

线性重度不可分

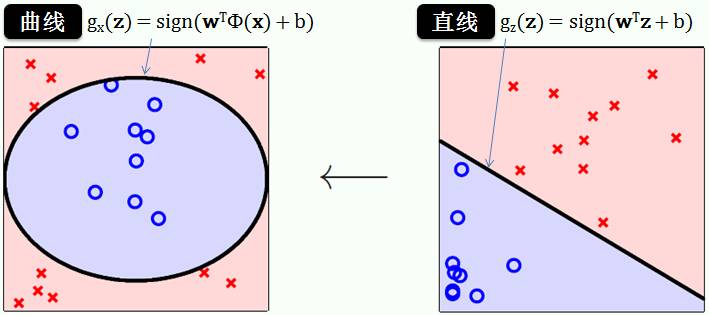
先从类型 2 开始，如果要做到正确分类每一个红叉和蓝圈，我们需要一个非线性函数。用 x1 和 x2 代表 x 空间的两个维度，做个平方转换如何？转换函数 Φ(x) 为

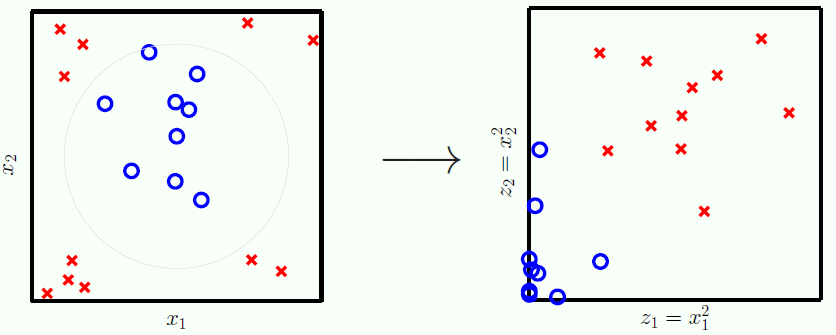
做完转换之后，红叉和蓝圈在 z 空间的位置如右图所示：

 

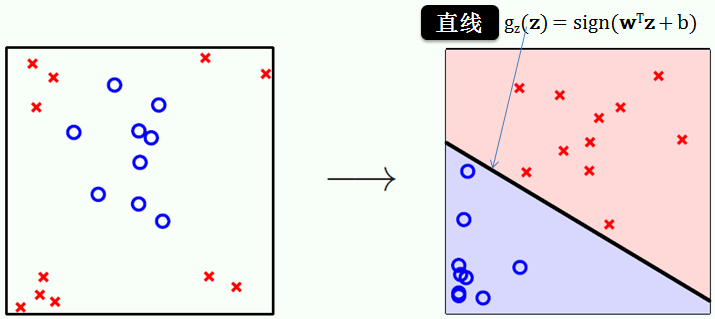
很明显，由左图 (x 空间) 可知，红叉在 x1 和 x2 维度上的绝对值都比蓝圈大 (红叉更扩散些)。平方转换之后，右图 (z 空间) 显示红叉在 z1 和 z2 维度上的值比蓝圈大，而且红叉和蓝圈在 z 空间里线性可分了哦。线性可分的问题解法上贴讲的已不能再详细，因此我们在 z 空间最大化间隔 (margin)，得到

    gz(z) = sign(wTz + b)

而不是

    gx(x) = sign(wTx + b)

从右上图可知在 z 空间的 SVM 是个线性函数，接着用转换函数 Φ(x) 得到在 x 空间的 SVM：

    gx(x) = gz(z)

              = gz(Φ(x))

              = sign(wTΦ(x) + b)

数据探测

 

假设用二次规划解得 w = [1, 1], b = -0.6 那么对应的 SVM 为

现在有两个问题要考虑：

1. 不同的转换函数 Φ 会得到不同的 SVM 吗？

2. 这个转换函数 Φ 是看到数据之前还是之后制定的？

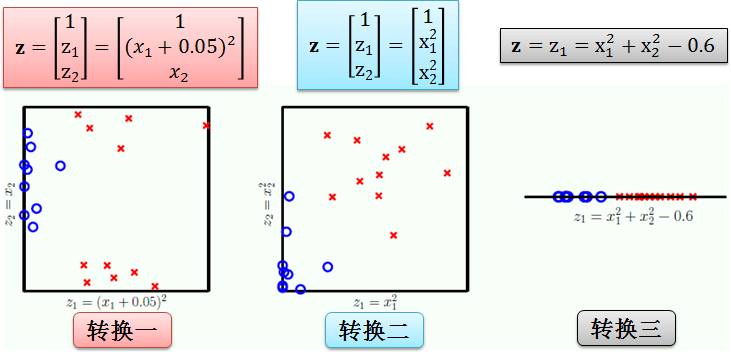
第一个问题答案是“会”，如下图：

• 转换一：只在 z1 维度上做手脚，z2 维度上不变

• 转换二：是我们上面做的平方转换

• 转换三：甚至不要 z2 维度

这三种转化都可以得到对应的 SVM，但是转换一里的 0.05 和转换三里的 0.6 完完全全是看完数据之后而决定的。

第二个问题答案是“看到数据之后”，这种现象叫做数据探测 (data snooping)，应该绝对避免，否则你看着数据来制定转换函数，是一种作弊行为。结果就是得到的 SVM 在你手头的上数据表现很好，换一套新数据表现就不行了，也就是泛化能力不够好。

 

我们必须在看到数据之前来选择转换函数 Φ，可以用多项式函数，高斯函数等，在小节 2.2 和 2.3 会细讲此问题。

软间隔SVM

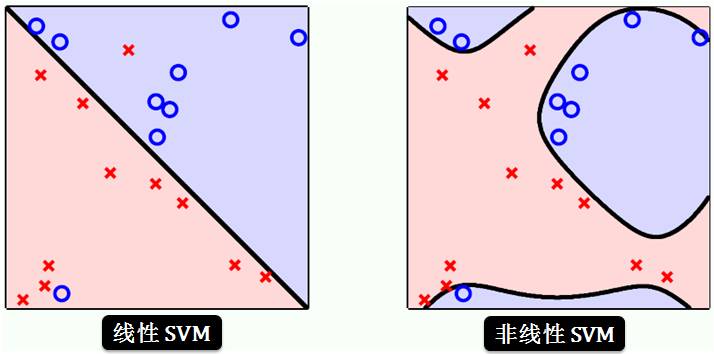
转化函数有无穷无尽，可以从低维度 x 空间转到高维度 z 空间 (高次多项式函数) 甚至无限维度 z 空间 (高斯函数)。但是维度越高，得到 SVM 越容易过拟合数据，如下图所示：

 

 

左上图是用直线来分类红叉和蓝圈，除了两个异常点，该 SVM 对其它点分类正确；右上图是用曲线 (极其怪异) 来分类红叉和蓝圈，该 SVM 对所有点都分类正确。你会选择哪一个 SVM？

不出所料，大家都会选择左图的线性 SVM，原因就是它没有过拟合数据，没人会为了两个异常点的精度而生成右图的怪异 SVM。但是本身这个数据的确是线性不可分，那么上贴讲的硬分隔 (hard-margin) SVM 就不适用了，怎么办呢？硬的不适用，你就软点呗，不可能完美分类每个点，你就允许点误差呗，于是将硬分隔 SVM 改成软分隔 (soft-margin) SVM 不就行了么？

本帖内容

 

本帖要解决这两种线性不可分问题，它们是

• 引进“转换函数 Φ”将低维空间转换到高维空间来解决类型 2 问题

• 引进“违规数据到边界的距离 ξ”将硬分隔更新成软分隔来解决类型 1 问题

和上贴的线性硬分隔 SVM 相比，上面两种操作直接用二次规划 (quadratic programming, QP) 都会增大运算量。两种解药为

• 用“核函数技巧” (kernel trick) 来降低类型 2 问题的计算量

• 用“序列最小优化”(sequential minimal optimization) 算法来降低类型 1 问题的计算量

目录

第一章 - 前戏王

    1.1 按部就班与投机取巧

    1.2 坐标下降法

第二章 - 理论皇

    2.1 数学符号

    2.2 空间转换

    2.3 核技巧

    2.4 软间隔 SVM 原始问题

    2.5 软间隔 SVM 对偶问题

第三章 - 实践狼

    3.1 软间隔 SVM 原始问题

    3.2 软间隔 SVM 对偶问题

    3.3 核 SVM 对偶问题

    3.4 SMO 算法

    3.5 模型选择

总结和下帖预告

附录

    1 软间隔 SVM 对偶问题推导

    2 SMO算法推导

第一章 - 前戏王

1.1

按部就班与投机取巧

计算 (1 + 2∙3 + 4∙5)²，用下面两种方法

你会用哪种方法？方法 1 是按部就班的算法，将括号里所有项都用平方展开，方法 2 是投机取巧的算法，将括号里所有项先合并再平方？如果你选择方法 2，恭喜你，你完全可以弄懂小节 2.3 讲的核技巧 (kernel trick)，如果你选择方法 1，呵呵…

1.2

坐标下降法

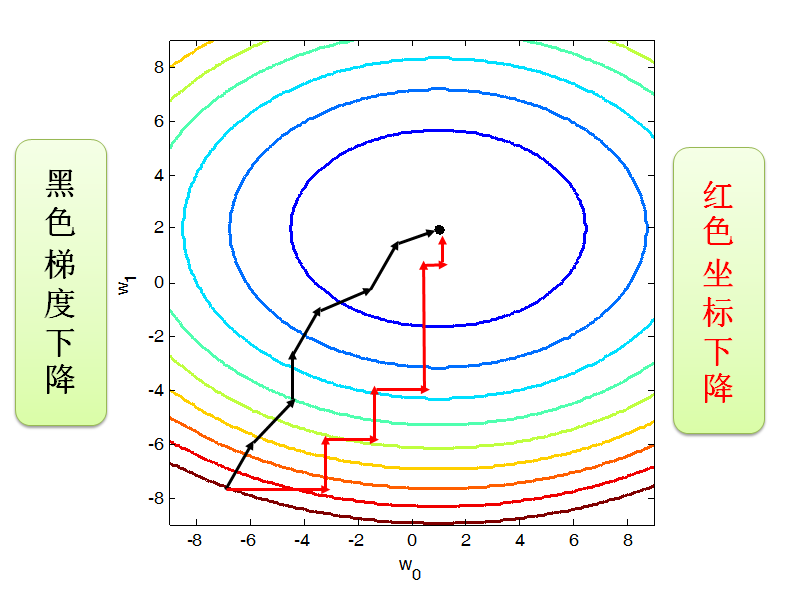
坐标下降方法是一种下降方法，但是和梯度下降 (gradient descent)不同，坐标下降法采用一维搜索，也就是说在每次迭代过程中，下降方向都是平行与坐标轴的。下图展示用梯度下降和坐标下降的找到最小值的路径。

梯度下降法是利用目标函数的梯度来确定搜索方向的，该梯度方向可能不与任何坐标轴平行。而坐标下降法方法是利用当前坐标方向进行搜索，不需要求目标函数的导数，只按照某一坐标方向进行搜索最小值。

通常来说坐标下降法会比梯度下降法慢一些，但是对于一些在某些点没有导数的函数，梯度下降法就用不了了，而坐标下降法还适用。

小节 3.4 会用到

第二章 - 理论皇

2.1

数学符号

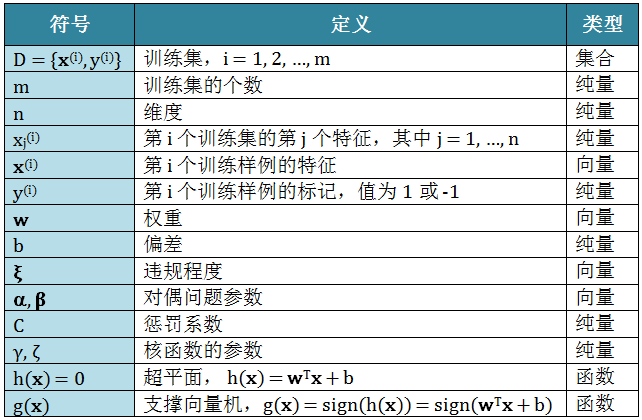
首先，列出全文需要用的数学符号：

2.2

空间转换

引言里已说明“看完数据之后再选取一个特殊转换函数会导致 data snooping”，就引言里的例子而言，保险起见，我们应该在看数据之前考虑一个更加广泛 (generic) 的 2 次多项式作为转换函数。

特殊转换函数和广泛转换函数的表达形式如下，在 x 空间里，前者得到的椭圆或双曲线方程中心点为 (0, 0)，有一定的局限性；而后者的椭圆或双曲线方程中心点可以是任意点，有一般性。如果换一套数据，数据点由 (2, 1) 往外扩散，前者肯定不适用，而后者通过调整 x1x2 前面的系数来适应这套数据。

当然我们可以用广泛的 Q 次多项式作为转换函数，比如

上面的数据 x 来自 2 维空间，通过 4 次多项式转换已变成了 15 维的 z 空间了。一般来说，令

    n 代表 x 空间的维度

    Q 代表多项式次数

    d 代表 z 空间的维度

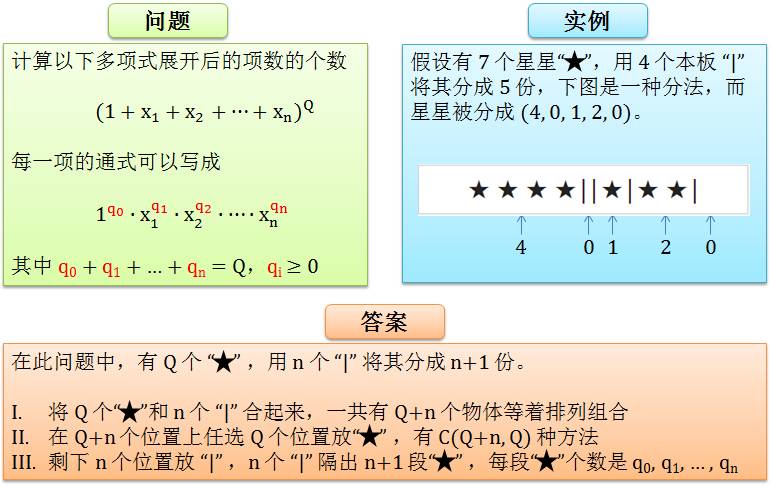
那么我们有 d = C(Q+n, Q)，在以上特例中 d = C(4+2,4) = C(6, 4) = 15。关于 d 的表达式的证明如下图，通过“问题⇨ 实例⇨ 答案”这个流程来看。

因此做这样一次转换的复杂度是 O(d)，将空间转换的概念带入 SVM 的原始问题来，我们得到

从上表可看出 z(i) 和 x(i) 在 SVM 原始问题中，在各种空间中，的位置是等价的，因此可以根据 x 空间的 SVM 对偶问题类比出 z 空间的 SVM 对偶问题，如下表：

因为从 x(i) 到 z(i) 的转换的复杂度是 O(d)，那么从计算 (x(k))Tx(i) 到 (z(k))Tz(i)  的复杂度也是 O(d)。由此看出这种“从低维度空间 x 转换高维度空间 z 来解 SVM 对偶问题”的做法带来的代价就很昂贵，有什么办法可以降低这个代价呢？答案是用核技巧 (kernel trick)。

2.3

核技巧

回忆上贴支撑向量机(上)中得到的硬线性分隔 SVM 对偶问题和它的最优解

上式所有红色部分都是 aTb 这样的形式，一个转置向量乘上一个向量，而它也可以用内积形式表现出来，如 aTb = <a, b>。

上一小节已讨论过，要从 x 空间转换成 z 空间，就必须要从计算 xTx' 到计算 zTz'。定义 K

    K(x, x’) = zTz' 

为核函数 (kernel function)，那么计算 K 有两种方法 (回顾小节1.1)：

1. 老实算法：先计算 z = Φ(x), z’ = Φ(x’)，再求 zTz'

2. 巧妙算法：不做转换动作而直接计算 zTz'

老实算法肯定算得出来，但是复杂度很高；而巧妙算法就是大名鼎鼎的核技巧 (kernel trick)。举个最简单的例子，假设 x 的维度 n = 2，以二次多项式 (Q = 2) 转换为例：

计算它们的内积再整理得

从上式看出，计算 zTz' 的确没有“显性”用到转换函数 Φ，而且 zTz' 还可以和 xTx' 建立起关系。为了能让 zTz' 的表达式整理的更漂亮些，我们将转换函数中的某项前面加一些系数 (两个转换函数是等价的，系数只是一个放缩因子，(x1, x2) 和 (ax1, bx2) 展开的是同样的空间)。

再计算它们的内积再整理得

结果是不是奇美无比？通过巧妙的设定一些系数，我们可以不费力气的计算出K(x,x') 。最后这个二次多项式就叫做二次多项式核函数，或简称二次多项式核。 下面来看看更多例子 (对任意 n 和 Q)。

多项式核

当 Q = 2，n 很大时，用下面转换函数：

计算它们的内积有

复杂度从老实算法的 O(n2) 降到了巧妙算法的 O(n)。

如果改用下面转换函数：

计算它们的内积有

上面的二次多项式是一般二次多项式核函数，由参数 ζ 和 γ 来描述。

---

当 Q 和 n 都很大时，类比二次多项式核得到 Q 次多项式核

虽然没有写出它所对应的转换函数 Φn 和内积计算，但是不难得到复杂度从老实算法的 O(nQ) 降到了巧妙算法的 O(n)。核技巧在手，所有内积只需要 O(n) 来求。

高斯径向基函数核

 

下面的核更加疯狂，高斯径向基函数核 (Gaussian-RBF kernel)，这里 RBF 全称是 radial basis function，该函数 r(x,x') 测量的某一点到另一点的距离，定义如下

高斯 RBF 核只是 RBF 函数中的一种，定义如下 (γ > 0)：

如果说多项式核是从低维度到高维度，那么高斯 RBF 核是从从低维度到无限维度！从核函数表面看很普通吧，怎么会扯到无限维度呢？为了便于说明，我们令 γ = 1 而且只考虑一维情况 (x 是纯量而不是向量)

根据其核，可以反推出对应的转换函数

如果你用老实算法计算内积，复杂度为 O(∞) 根据不可能算出来，但运用高斯 RBF 核计算内积只需要 O(n)。

核函数性质

从上面看，多项式核和高斯 RBF 核可以看出核函数相当好用，当然还有其他的核函数也非常好用，那么什么样的函数才是正确 (valid) 的核函数呢？根据上述操作，一个正确的核函数必然能够写成两个映射函数内积的形式。严谨来说有个 Mercer 定理来帮助我们识别核函数，定理如下：

给定一个 K，那么 K 是合法的核的充分必要条件是对于任何一个数据集，对应的核矩阵式是对称 (symmetric) 半正定 (positive semi-definite) 矩阵。

证明

对一个数据集 {x(1), x(2), …, x(m)}，定义一个 m 乘 m 的矩阵 K

因此矩阵 K 对称，此外对于任意向量 v，有

因此 K 是对称半正定矩阵。

2.4

软间隔 SVM 原始问题

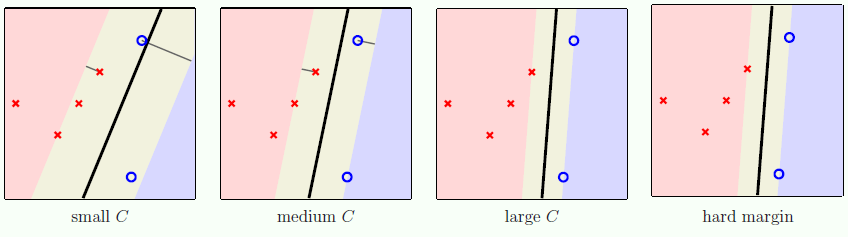
硬间隔 SVM 要求所有得数据都要分类正确，在此前提下再最小化 wTw，但是现实中这种事情很少发生 (即没有这样一个完美的数据让你所有分类正确)。那么你要放弃这个问题，还是要试试另外一种方法，即软间隔 SVM？

软间隔 SVM 就是为了缓解“找不到完美分类数据”的问题，它会容忍一些错误的发生，将发生错误的情况加入到目标函数之中，希望能得到一个错分类情况越少越好的结果。为了能一目了然发现硬间隔和软间隔 SVM 原始问题之间的相似和不同之处 (红色标示)，将它们的类比形式展示在下表：

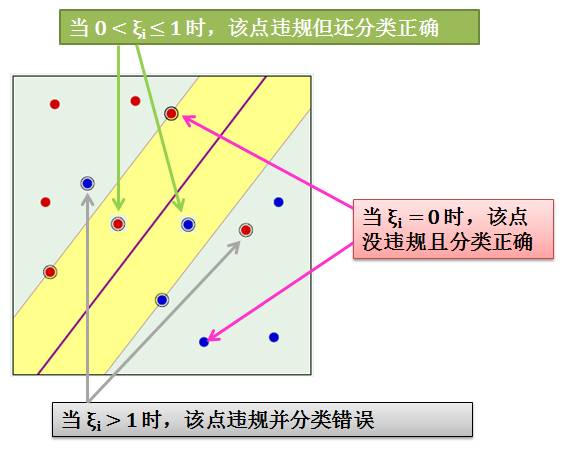
由上发现硬间隔和软间隔 SVM 的区别就是后者多了 ξ 和 C，参数ξ是衡量数据犯了多大的错误，而不是数据犯了几个错误。为了简化令 u_i = y(i)(wTx(i) + b)：

• 当 ξ_i = 0 时，该点没有违规而且分类正确，因为 u_i ≥ 1，该点离分隔线距离大于等于 margin

  
  

• 当 0 < ξ_i ≤ 1 时，该点违规了但还是分类正确，因为 u_i 大于“一个小于1”的正数，该点离分隔线距离小于 margin

  
  

• 当 ξ_i > 1 时，该点违规了并分类错误，因为 u_i 大于一个负数 (u_i 可能小于0)，我们知道只有 u_i > 0 是分类正确

上述讨论情况在下图中展示

总结来说，用 ξ 来记录违规数据距离边界的距离，并将这个距离纳入到最佳化的标准里面。但是我们不希望 ξ 太大，因为这意味着有某个数据分类错的太离谱，因此需要用 C 来惩罚太大的ξ。参数 C 控制“到底要多大的边界”还是“更加在意违反边界的情形越少越好”。

• 越大的 C 代表，宁可边界窄一点，也要违规 (甚至出错) 数据少点

• 越小的 C 代表，宁可边界宽一点，即便牺牲分类精度也无所谓

2.5

软间隔 SVM 对偶问题

回顾上节的软间隔 SVM 的原始问题

其对应的拉格朗日量 (Lagrangian)

写出软间隔 SVM 的对偶问题

根据附录 1 的详细推导，我们得到标准化软间隔 SVM 的对偶问题

原始问题是通过求 b 和 w 来最小化目标函数，而对偶问题是通过求 α 来最小化目标函数，其矩阵形式为

为了能一目了然发现硬间隔和软间隔 SVM 对偶问题之间的相似和不同之处，我们将它们的代数形式和矩阵形式的类比展示于下表：

一言以蔽之，硬间隔和软间隔 SVM 的唯一区别就是 α_i 的范围

    硬间隔 SVM：α_i ≥ 0

    软间隔 SVM：0 ≤ α_i ≤ C

第三章 - 实践狼

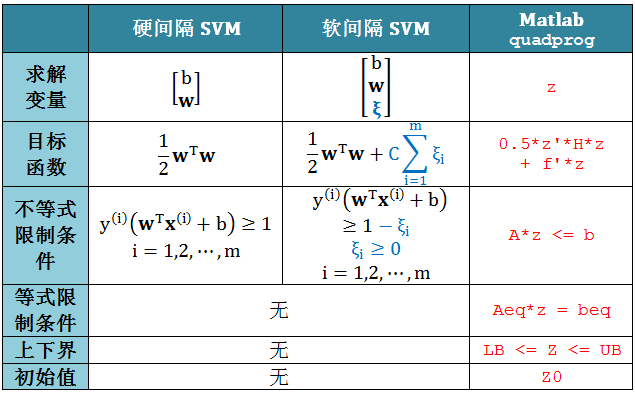
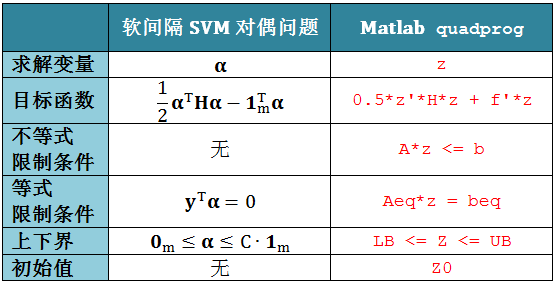
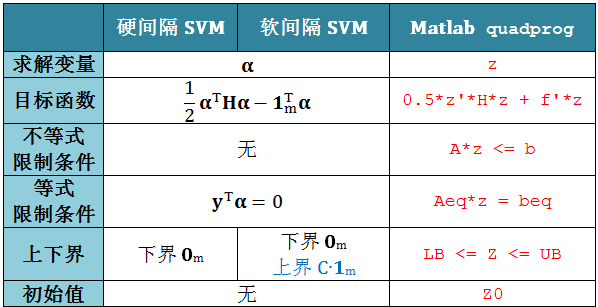
小节 3.1 到 3.3 都会用 Matlab 里面的 quadprog 函数：

3.1

软间隔 SVM 原始问题

回顾软间隔 SVM 的原始问题

类比硬间隔 SVM 和 quadprog 函数参数的对应关系，下表给出软间隔 SVM 

和 quadprog 函数参数的对应关系

---

类比“目标函数”得到：

---

类比“不等式限制条件”得到：

---

类比“等式限制条件”、“上下界”和“初始值”得到：

 

Aeq = [], beq = [], LB = [], UB = [], Z0 = []

---

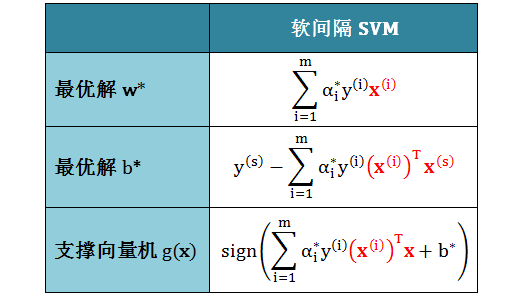
利用 quadprog 函数解出原始问题的最优解，记为 b* 和 w*，以及支撑向量机 g(x) = sign(wTx + b*)

3.2

软间隔 SVM 对偶问题

回顾软间隔 SVM 的对偶问题

为了用 Matlab 里面的 quadprog 函数，我们必须做一点调整，如下表

---

类比“目标函数”得到：

---

类比“等式限制条件”得到：

---

类比“上下界”得到：

---

类比“不等式限制条件”和“初始值”得到：

A= [], b = [], Z0 = []

---

利用 quadprog 函数解出对偶问题的最优解，记为 α*。则相应的最优解 b* 和

 w*，及 SVM g(x) 结果如下表 (对某个 α*s > 0，即所谓的支撑向量)：

3.3

核 SVM 对偶问题

由于对偶问题的目标函数中有 x 的内积表达形式，而核函数的本质就是将低维度的 x 转为高维度的 z，将 x 的内积用 z 的内积代换。因此核 SVM 通常用在对偶问题而不是原始问题，当然这个对偶问题可以是硬间隔或软间隔的 SVM，问题的矩阵表达形式如下：

为了用 Matlab 里面的 quadprog 函数，我们必须做一点调整，如下表

---

类比“目标函数”得到：

---

类比“等式限制条件”得到：

---

类比“上下界”得到：

---

类比“不等式限制条件”和“初始值”得到：

A= [], b = [], Z0 = []

---

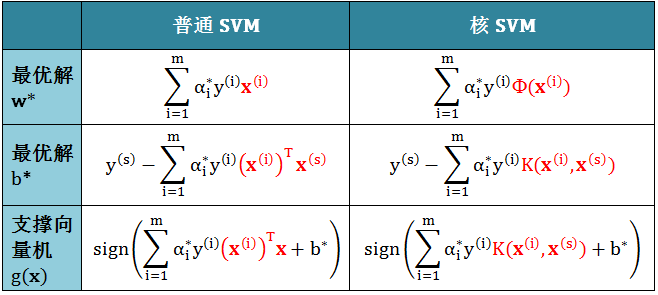
利用 quadprog 函数解出对偶问题的最优解，记为 α*。类比核 SVM 和普通 SVM 的最优解 b* 和 w*，以及 g(x) ，只需做以下两个改动：

1. 将 x 用 Φ(x) 替换

2. 将 xTx’ 用 K(x, x’) 替换

类比结果如下表 (对某个 α*s > 0，即所谓的支撑向量)：

3.4

SMO 算法

当数据量很大时，用 QP 解软间隔 SVM 对偶问题就会非常耗时。这时候 John C. Platt 发明的序列最小优化 (Sequential Minimal Optimization) 算法，简称 SMO 算法，就可以派上用场了。

首先回顾要解的最优化问题：

SMO 算法的灵感来自坐标下降法 (见小节 1.2)，即每次只优化一个变量 α_i (而固定其他变量 α_j, j ≠ i) 求解目标函数的最小值。但是此问题有个限制条件 Σiα_iy(i) = 0，当只变 α_i 时，上述限制条件会被打破。为了克服以上的困难，SMO 采用一次更新两个变量的方法。

根据 KKT 里的原始约束 (Primal Feasible)、对偶约束 (Dual Feasible) 和互补松弛 (Complementary Slackness) 条件得到的关系式

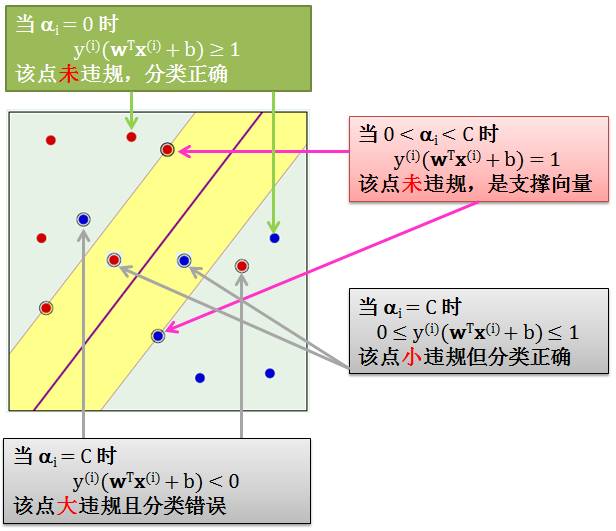
为了简化令 u_i = y(i)(wTx(i) + b)，分情况讨论

• 当 0 < α_i < C 时，由 (iii) 得到 u_i = 1 – ξ_i，由 (iv) 得到 ξ_i = 0。我们有 u_i = 1 因此对应的数据在边界上 (支撑向量 SV)

  
  

• 当 α_i = 0 时，由 (i) 和 (iii) 得到 u_i ≥ 1 – ξ_i，由 (iv) 得到 ξ_i = 0。我们有 u_i ≥ 1 因此对应的数据在边界的外面 (未违规数据)

  
  

• 当 α_i = C 时，由 (ii) 和 (iv) 得到 ξ_i ≥ 0，由 (iii) 得到 u_i = 1 – ξ_i。我们有 u_i ≤ 1因此对应的数据在边界得里面 (违规数据)。再细分下，当 0 ≤ u_i ≤ 1 时，数据小违规但分类正确；当 u_i < 0 时，数据大违规且分类错误

上述讨论情况在下图中展示

这样我们得到 SMO 算法需要的收敛条件，如下

有了以上收敛条件，我们可以来设计 SMO 算法，具体推导见附录 2。

3.5

超参数和模型选择

在使用 SVM 的时候，根据不同的数据特征，一般都会用软间隔 SVM 加上一个核函数。那么问题来了，模型里面的超参数 (hyper-parameter) 该如何选择？

比如，软间隔 SVM 里面的超参数 C、多项式核里面的超参数 γ, ζ，还有高斯 RBF 核里面的超参数 γ 该如何选择。很简单，用验证集 (validation set) 或者交叉验证集 (cross-validation set)，但是在选择它们之前，我们先看看它们的性质。

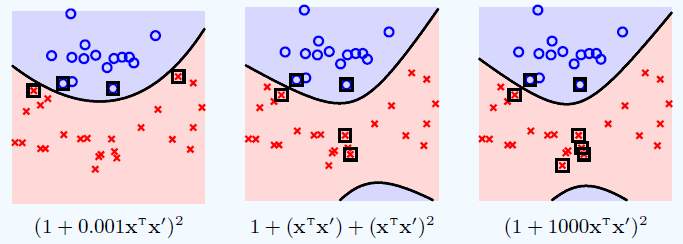
多项式核的超参数 γ, ζ

为了方便令 ζ = 1 而变动 γ。从上图可看出，这些都是二次多项式核函数，只不过系数不同，但是它们对应的是同一个空间 (系数只是缩放因子)，因此做事情的能力是一样的。不同的系数导致了不同的内积。不同的内积定义了不同的距离，不同的距离就有不同的几何特性，不同的几何特性对应不同的边界和支撑向量 (黑框里的点)。

从上图我们很难一眼看出哪个 SVM 更好，或哪个核更好，或哪个 γ 更好，我们需要用验证误差当标准来判断。但是当 γ = 0.001 时，边界没有下面凸起的那块，看起来更合理些。

多项式核首先需要设定多项式次数 Q 来控制模型，之后还要同时调参 γ, ζ，参数比较多选择起来比较麻烦。

高斯 RBF 核的超参数 γ

高斯 RBF 核非常强大，几乎可以找出任何边界，但在 γ 很大的时候仍有问题。首先 SVM 这种最大化间隔的机制就是为了防止过拟合，但是你看 γ = 100 时 (右图)，数据过拟合成什么样子。从上图看 γ = 1 是个不错的选择。

 

高斯 RBF 核只有一个参数，比较好选择，但由于它是无限多维，没有什么物理意义，很难解释给外人。

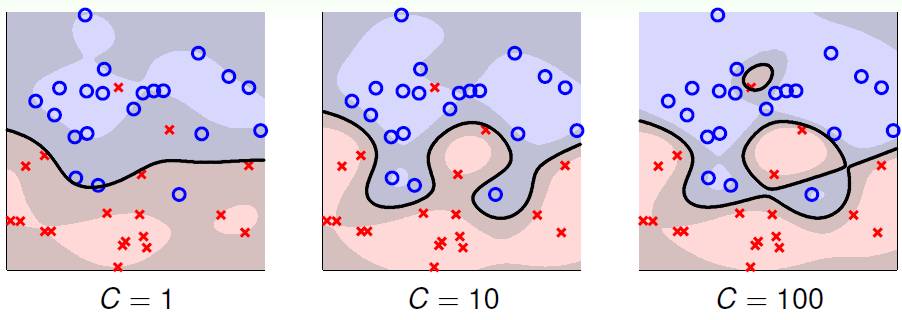
软分隔的超参数 C

上图 (使用高斯 RBF 加核软间隔 SVM) 展示着不同 C 的值的不同的分类效果。蓝色区域表示蓝圈的区域，红色区域表示红叉的区域，灰色区域表示边界部分，也是存在错误的情况。

• 当 C = 1 时，灰色区域很宽，犯错的数据很多

• 当 C = 10 时，用比较大的C来控制分类并尽量减少错误，发现灰色区域变窄了，犯错的数据减少了

• 当 C = 100 时，灰色区域更窄了，犯错的数据更少了，但是会出现过拟合的问题 (边界开始成环形，而且还有一个封闭小圈)

在小节 1.4 回忆 C 的定义，

• 越大的 C 代表，宁可边界窄一点，也要出错的数据少一点

• 越小的 C 代表，宁可边界宽一点，即便牺牲分类精度也无所谓

上图验证了 C 和边界的关系，随着 C 增大，边界越来越窄，而且违规数据也越来越少。其中违规数据有两类：

1. 进入灰色区域但没跨过边界，分类仍然正确但快不正确了

2. 进入灰色区域并跨过边界，分类错误

当 C 很大时，软间隔 SVM 慢慢像硬间隔 SVM 收敛，原因更简单，C 无穷大时，ξ = 0，这意味着没有数据分类错误。

模型选择

 

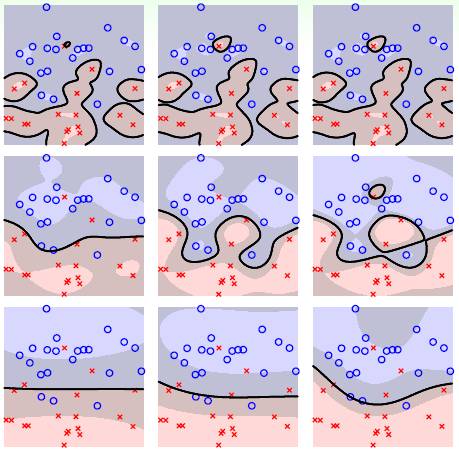
下图表示的是使用高斯 RBF 核的软间隔 SVM 在不同的 C 和 γ 下的边界表现，其中横轴对应 C，纵轴对应 γ。

计算每个 C 和 γ 下的交叉验证误差，选择误差最小的那个模型参数，由下图看，左下角图显示误差为 0.1750 最小，应该选它对应的 C 和 γ。

总结和下贴预告 

本帖讨论的是核技巧和线性软间隔 SVM。

核技巧就是在“不触碰高维空间的情况下”计算高维向量内积，而软间隔 SVM 是允许分类错误发生的 SVM。软间隔 SVM 加上核技巧是最有用的分类模型之一，它是一个强鲁棒性的线性模型和用核函数做非线性转换的结合。

再总结一下SVM分类遇到的不同数据种类

    类型1 - 线性可分

    类型2 - 线性不可分，升维后线性可分

    类型3 - 线性不可分，升维后线性不可分

但是现实中哪有类型 1 的数据，都是理论中举的例子，此外，类型 2 的数据可能有，但是谁又能保证升维后真的线性可分呢？因此现实中几乎都是类型 3 的数据，那么只能用带核技巧 (为了升维) 的软间隔 SVM (为了处理线性不可分)。这样做其实没什么损失，假设真的线性可分，大不了那些 ξ 都是零嘛。

确定好核函数 (比如多项式或高斯 RBF)，之后就用验证误差或者交叉验证误差来选择核对应的参数，以及软间隔 SVM 里面的参数 C。

下帖是图解神经网络，Stay Tuned!

作者现在正在小象学院上一些关于量化投资的课，该学院不允许将课件以任何形式分享。作者本身也是 FRM 和 CAIA，对里面讲的理论知识还是比较熟悉的，只不过欠缺的是实操经验。作者会根据学习的内容，加上大量的自己的心得体会，并写成文章和大家一起学习！

附录

1

1

软间隔 SVM 对偶问题推导

对偶问题如下

求解过程分两步：

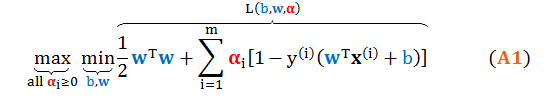
1. 固定 α_i, β_i，最小化 L(b,w,ξ,α,β) 求出 b 和 w 的最优解

2. 将最优解带入上式再最大化目标函数求出 α_i, β_i 的最优解

第一步是一个无约束规划，非常简单，求 L(b,w,ξ,α,β) 的梯度。首先求 L 对 ξ 和b 求偏导数设为 0 解得

利用上面结果将 (A1) 化简为

其中第一步用了 C = α_i + β_i，第二步消除 b 前面的系数。

再求 L 对 w 求偏导数设为 0 解得

第二步是利用上面结果将 (A1) 进一步化简为 (将 w 带入)

在目标函数前面加个负号，将最后一步求最大值转换成求最小值，因此 (A1) 最终变成

2

SMO 算法推导

符号制定

假设 SMO 算法在某次更新时，需要更新的变量为 α₁ 和 α₂，则其余变量都可以视为常量。为了描述方便，定义

SMO 算法是一个迭代算法，因此有初始条件和终止条件

等价问题

 

目标函数可以简化成 (舍弃不含 α₁ 和 α₂ 常数项)

α₂ 上下界

 

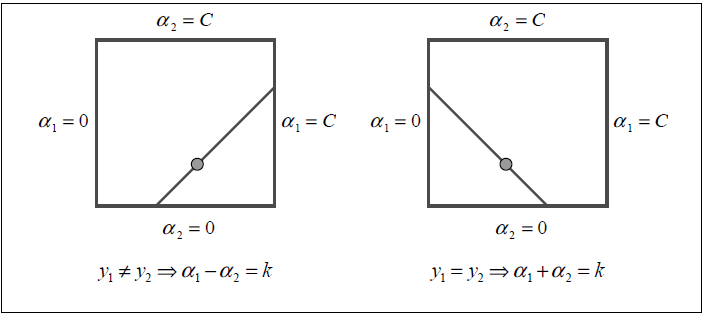
根据对偶问题的约束条件可知，α₁ 和 α₂ 本身都在 [0, C] 之间。再在上面问题的约束条件两边同乘以 y(1) 得到 α₁ + sα₂  = w。现在结合这两个条件我们来进一步明确 α₂  的上界 H 和下界 L。

因为 s = y(1)y(2)，我们根据 y(1) 和 y(2) 同号和异号的情况讨论，如下图：

• 当 y(1) ≠ y(2)，s = -1，则 α₂ = α₁–w，斜率向上，如左图

• 当 y(1) = y(2)，s = 1，则 α₂ = –α₁–w，斜率向下，如右图

根据上图很容易得到 α₂ 的上下界

注意 SMO 是迭代算法，L 和 H 里面的 α₁ 和 α₂ 是上一步迭代计算出来的值。

最终问题

 

继续化简上式，代入 vi 和 s，并用 α₂ 代替 α₁

求解 α₁ 和 α₂

 

求目标函数 L 关于 α₂ 的导数并设为零，有

结合以下条件

解得

根据 α₂ 的上下界更新其值

进而解出 α₁ 的值

求解 b

最后 b 在每一步迭代都需要计算，再每一步都要检查以下 KKT 条件。

情况 1：当 α₁ 在而 α₂ 不在 [0, C] 之间

情况 2：当 α₂ 在而 α₁ 不在 [0, C] 之间

情况 3：当 α₁ 和 α₂ 都在 [0, C] 之间，b1 = b2 都是解，因此任取一个即可。

情况 4：当 α₁ 和 α₂ 都不在[0, C] 之间，b1 和 b2 满足 KKT 条件，因此取个平均值 (b1+b2)/2 即可。

综合各种情况，得到 b 值为