从示例中理解SVM算法（附代码）

作者：Sunil Ray

编译：Bot

编者按：掌握机器学习算法并不是什么神话。对于大多数机器学习初学者来说，回归算法是很多人接触到的第一类算法，它易于理解、方便使用，堪称学习工作中的一大神器，但它真的是万能的吗？通过这篇文章，论智希望大家明白，有时候，生活中的一些万金油工具其实并不是我们的唯一选择。

如果把机器学习看做是一个堆满刀、剑、斧、弓等兵器的军械库，里面有成千上万种工具，我们的选择余地的确很大，但我们应该学会在正确的时间和场合使用正确的武器。如果把回归算法看作是其中的剑，它可以轻松刺穿敌人（数据）的坚甲，但不能被庖丁用来解牛。对于这类问题高度复杂的数据处理任务，一把锋利的“小刀”——支持向量机（SVM）往往更有效——它可以在较小的数据集上工作，并构建出更强大的模型。

目录

1. 什么是支持向量机？

2. SVM的工作原理

3. 如何在Python和R中实现SVM

4. 如何调整SVM参数

5. SVM的优点和缺点

1. 什么是支持向量机？

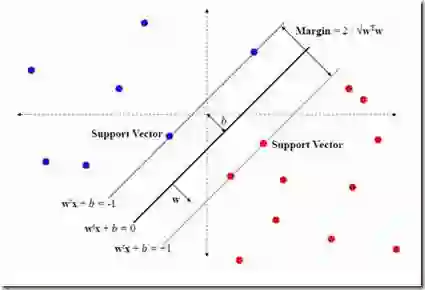
在机器学习领域中，支持向量机”（SVM）是一种可用于分类和回归任务监督学习算法，在实践中，它的主要应用场景是分类。为了解释这个算法，首先我们可以想象一大堆数据，其中每个数据是高维空间中的一个点，数据的特征有多少，空间的维数就有多少。相应的，数据的位置就是其对应各特征的坐标值。为了用一个超平面尽可能完美地分类这些数据点，我们就要用SVM算法来找到这个超平面。

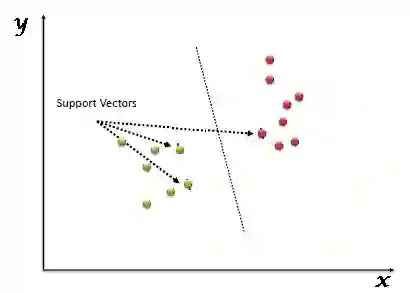
在这个算法中，所谓“支持向量”指的是那些在间隔区边缘的训练样本点，而“机”则是用于分类的那个最佳决策边界（线/面/超平面）。

2. SVM的工作原理

下面我们用图像演示如何找出正确的超平面的几种方法。

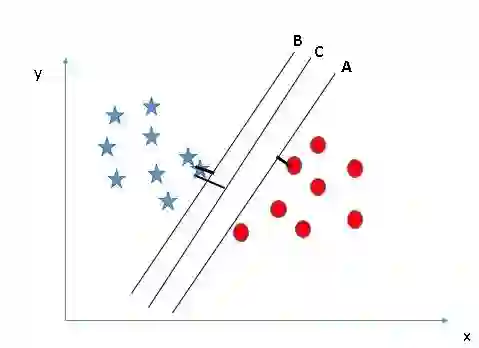
情景1

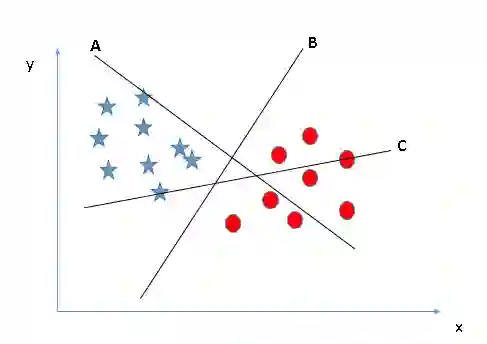
下图中有三个超平面：A、B和C。那么其中哪个是正确的边界呢？只需记住一点：SVM选择的是能分类两种数据的决策边界。很显然，相比A和C，B更好地分类了圆和星，所以它是正确的超平面。

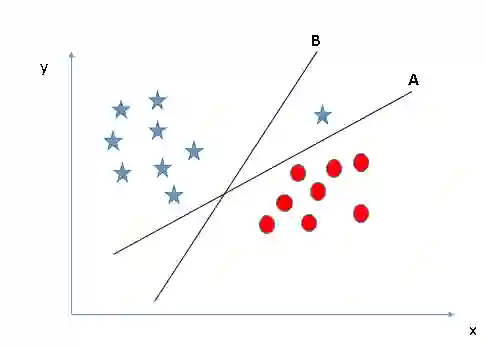
情景2

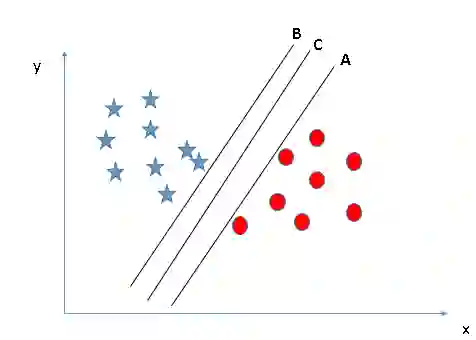
下图中同样有A、B、C三个超平面，和情景1不同，这次三个超平面都很好地完成了分类，那么其中哪个是正确的超平面呢？对此，我们再修改一下之前的表述：SVM选择的是能更好地分类两种数据的决策边界。

在这里，我们可以绘制数据到决策边界的距离来辅助判断。如下图所示，无论是星还是圆，它们到C的距离都是最远的，因此这里C就是我们要找的最佳决策边界。

之所以选择边距更远的超平面，是因为它更稳健，容错率更高。如果选择A或C，如果后期我们继续输入样本，它们发生错误分类的可能性会更高。

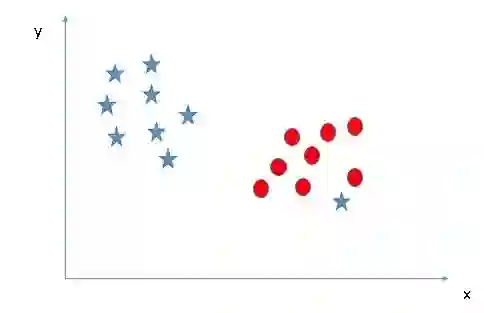
情景3

这里我们先看图，试着用上一情景的结论做出选择。

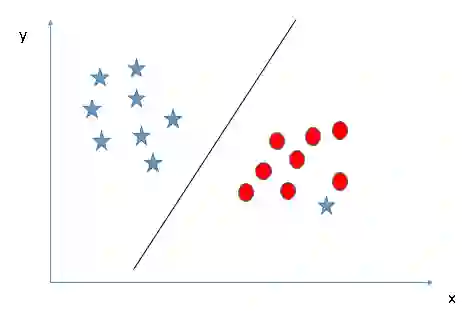
也许有些读者最终选择了B，因为两类数据和它的边距较A更远。但是其中有个问题，就是B没有正确分类，而A正确分类了。那么在SVM算法面前，正确分类和最大边距究竟孰重孰轻？很显然，SVM首先考虑的是正确分类，其次才是优化数据到决策边界的距离。情景3的正确超平面是A。

情景4

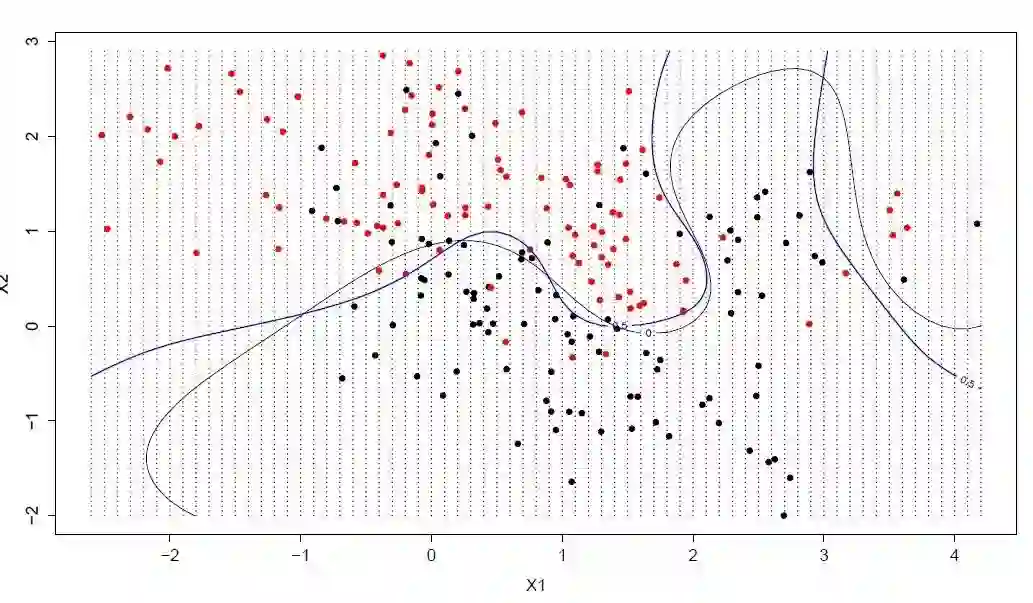
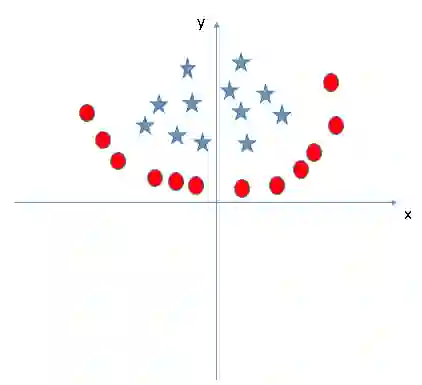
在前几个例子里，虽然我们把决策边界表述为超平面，但它们在图像中都是一条直线，这其实是不符合现实的。如在下图中，我们就无法用直线进行分类。

红色的圆点之间出现了一颗蓝色的星，并且它和其他同类数据不在同一侧。那么我们是否要绘制一条曲线来分类？或者说，是否要把它单独氛围一类？答案是否定的。

对比情景3，我们可以推断此处的星是一个异常值，所以在这里SVM算法不受分类前提困扰，可以直接在圆和星之间找出一个最合适的超平面进行分类。换句话说，SVM对于异常值是有效的。

情景5

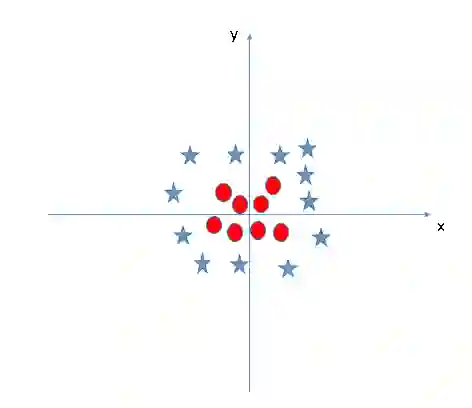
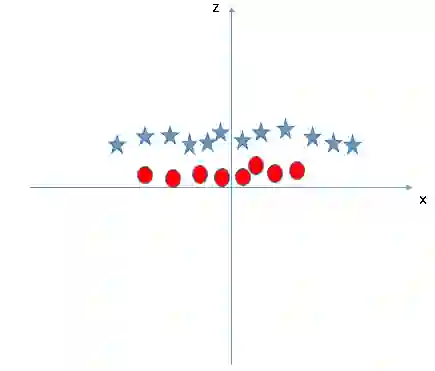
让我们继续关注直线这个话题。在下图中，两类数据之间已经不具备直线边界了，那么SVM算法会怎么分类？请想象电视剧中大侠拍桌震起酒杯的画面。图中目前只有X和Y两个特征，为了分类，我们可以添加一个新特征Z = X² + Y²，并绘制数据点在X轴和Z轴上的位置。

数据点被“震起来”后，星和圆在Z轴上出现了一个清晰的决策边界，它在上图中表示为一条二维的线，这里有几个注意点：

• Z的所有值都是正的，因为它是X和Y的平方和；

• 在原图中，圆的分布比星更靠近坐标轴原点，这也是它们在Z轴上的值较低的原因。

在SVM中，我们通过增加空间维度能很轻易地在两类数据间获得这样的线性超平面，但另一个亟待解决的问题是，像Z = X² + Y²这样的新特征是不是都得由我们手动设计？不需要，SVM中有一种名为kernel的函数，它们能把低维输入映射进高维空间，把原本线性不可分的数据变为线性可分，我们也称它们为核函数。

核函数主要用于非线性分离问题。简而言之，它会自动执行一些非常复杂的数据转换，然后根据你定义的标签或输出找出分离数据的过程。

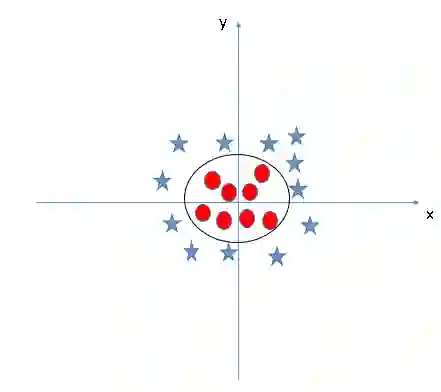
当我们把数据点从三维压缩回二维后，这个超平面就成了一个圆圈：

3. 如何在Python和R中实现SVM

在Python中，scikit-learn是一个受众极广的方便又强大的机器学习算法库，所以我们可以直接在scikit-learn里找到SVM。

#Import Library
from sklearn import svm
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create SVM classification object 
model = svm.svc(kernel='linear', c=1, gamma=1) 
# there is various option associated with it, like changing kernel, gamma and C value. Will discuss more # about it in next section.Train the model using the training sets and check score
model.fit(X, y)
model.score(X, y)
#Predict Output
predicted= model.predict(x_test)

对于R语言，e1071软件包可用于轻松创建SVM，它具有辅助函数以及Naive Bayes分类器的代码，和Python大体相同。

#Import Library
require(e1071) #Contains the SVM 
Train <- read.csv(file.choose())
Test <- read.csv(file.choose())
# there are various options associated with SVM training; like changing kernel, gamma and C value.
# create model
model <- svm(Target~Predictor1+Predictor2+Predictor3,data=Train,kernel='linear',gamma=0.2,cost=100)
#Predict Output
preds <- predict(model,Test)
table(preds)

4. 如何调整SVM参数

在机器学习中，调参是提高模型性能额一种有效做法，我们先来看看SVM中的可用参数。

sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma=0.0, coef0=0.0, shrinking=True, probability=False,tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, random_state=None)

这里我们只介绍几个重要参数的调参方法。

kernel：之前我们已经介绍了kernel是什么，关于它，我们可以挑选各种函数：线性的、RBF核的、poly函数等（默认值为RBF核）。对非线性超平面来说，后两种核函数效果显著。以下是几个例子：

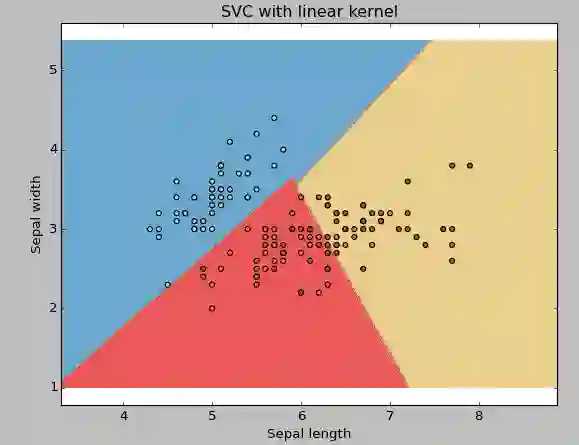
例1：线性核函数

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets

# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features. We could
 # avoid this ugly slicing by using a two-dim dataset
y = iris.target

# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0 # SVM regularization parameter
svc = svm.SVC(kernel='linear', C=1,gamma=0).fit(X, y)

# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
 np.arange(y_min, y_max, h))

plt.subplot(1, 1, 1)
Z = svc.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)

plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')
plt.show()

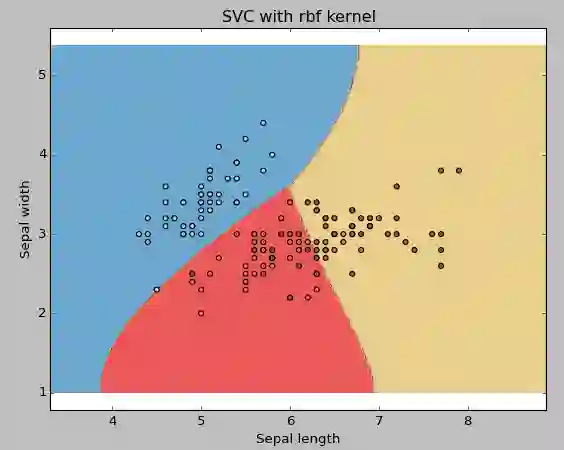
例2：RBF核函数

把核函数类型更改为rbf，然后从图中观察变化。

svc = svm.SVC（kernel ='rbf'，C = 1，gamma = 0）.fit（X，y）

如果你有大量特征（> 1000），我建议你选择线性内核，因为它们在高维空间内线性可分的概率更高。除此之外，那rbf就是个不错的选择，但是不要忘记交叉验证其参数来避免过拟合。

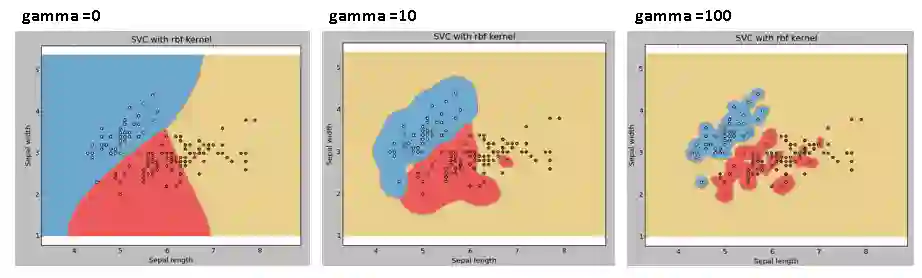
gamma：rbf、poly和sigmoid的核系数。gamma值越高，模型就回更努力地拟合训练数据集，所以它也是导致过拟合的一个要因。

例3：gamma = 0.01和100

svc = svm.SVC（kernel ='rbf'，C = 1，gamma = 0）.fit（X，y）

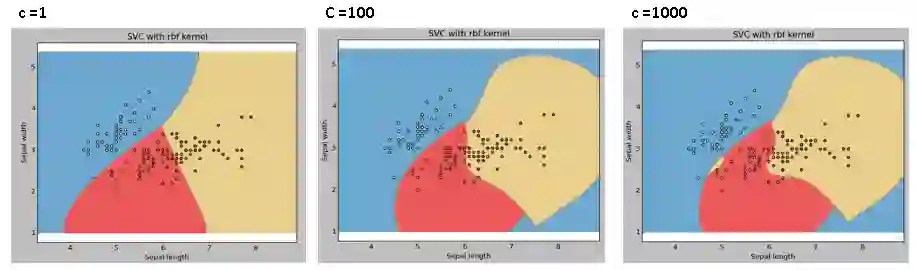
C： 误差项的惩罚参数C，它还控制着决策边界的平滑与否和正确分类训练点之间的权衡。

例4：C = 100和1000

自始自终，我们都要记得用交叉验证来有效组合这些参数，防止模型过拟合。

5. SVM的优点和缺点

优点

• 效果很好，分类边界清晰；

• 在高维空间中特别有效；

• 在空间维数大于样本数的情况下很有效；

• 它使用的是决策函数中的一个训练点子集（支持向量），所以占用内存小，效率高。

缺点

• 如果数据量过大，或者训练时间过长，SVM会表现不佳；

• 如果数据集内有大量噪声，SVM效果不好；

• SVM不直接计算提供概率估计，所以我们要进行多次交叉验证，代价过高。

小结

本文介绍了什么是支持向量机、SVM的工作原理、如何在Python和R中实现SVM、如何调参以及它的的优点和缺点。希望读者能在阅读完毕后动手试一试，不要受近年来出现的“有DL还要学SVM吗？”的说法的影响，经典的算法总有其可贵之处，它也是进公司面试时的一大热门题目。

如果不知道从何开始，可以尝试做做论智的这道题：

原文地址：www.analyticsvidhya.com/blog/2017/09/understaing-support-vector-machine-example-code/