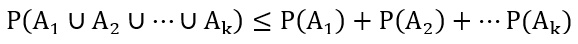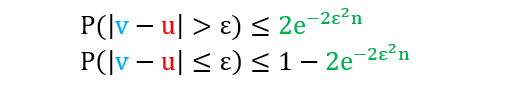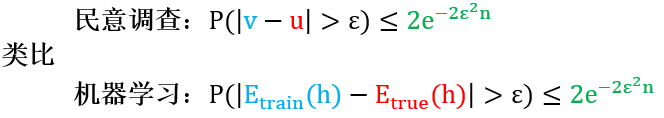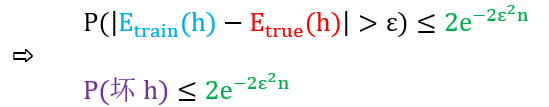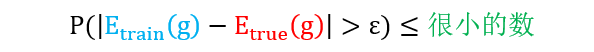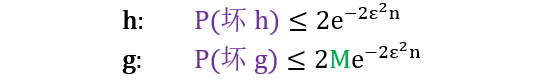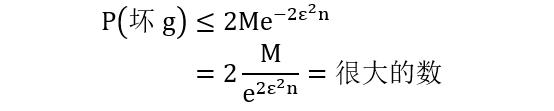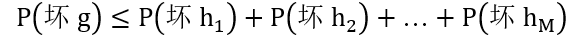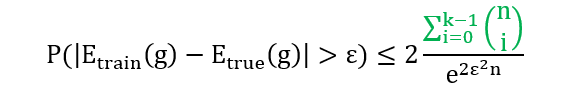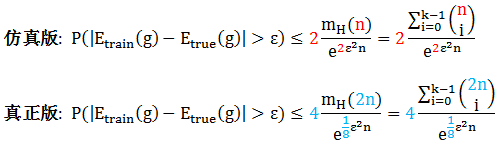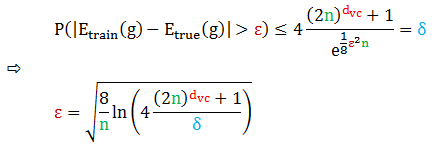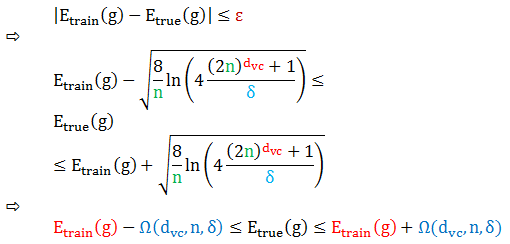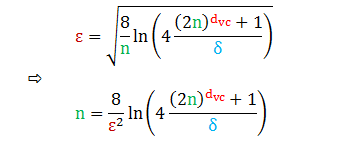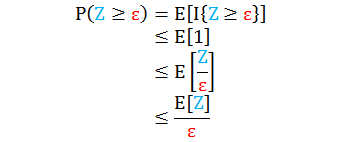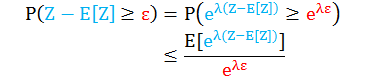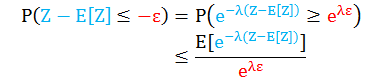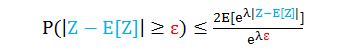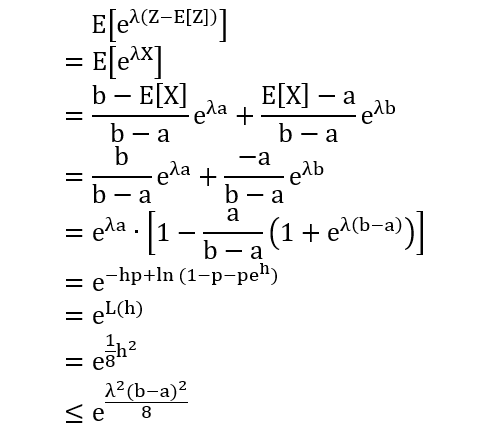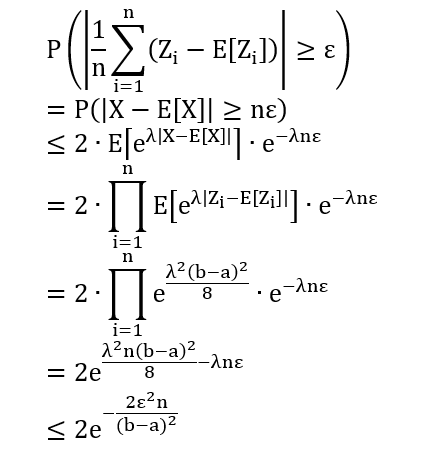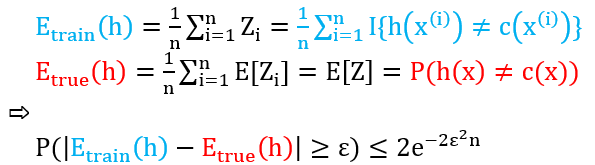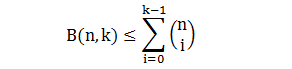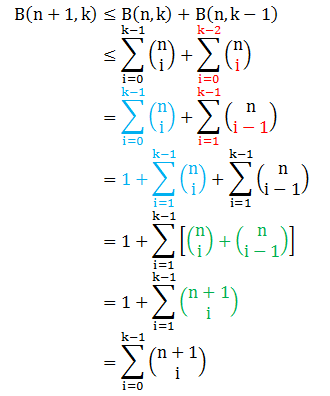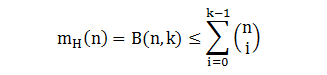计算学习理论

引言

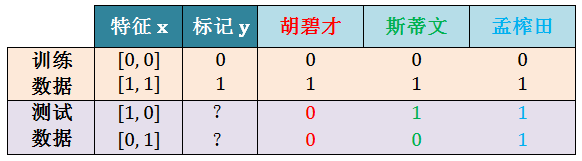
胡碧才，斯蒂文和孟榨田都是玩机器学习的，他们都觉得自己的模型厉害谁也不服谁。有一次他们来一场比赛，他们三个人的模型在前两个数据训练数据上表现非常好，模型的输出完全和样例真实标记一样。

其中 x = [x1, x2] 里面都是布尔型变量 (boolean variable)。

训练数据表现好不算什么，判断模型真的好坏还是要看在后两个测试数据上的表现，让人惊讶的是，他们三人在测试集上的结果完全不同。

• 胡碧才是胡逼猜，用丢硬币得出 0 和 0

• 斯蒂文是王圣元，用支持向量机得出 1 和 0

• 孟榨田是猛炸天，用 10 层神经网络得出 1 和 1

仅仅看他们的模型，孟榨田水平应该高于斯蒂文高于胡碧才，真是这样吗？现在假设 y 和 x 的真实函数 y = c(x) 关系是：

 

• c(x) = x1 ⋁ x2 ：孟砸田完胜

• 第 3 个 x = [1, 0]，因此 y = 1⋁0 = 1

• 第 4 个 x = [0, 1]，因此 y = 0⋁1 = 1

  
  

• c(x) = x1 ⋀ x2 ：胡碧才完胜

• 第 3 个 x = [1, 0]，因此 y = 1⋀0 = 0

• 第 4 个 x = [0, 1]，因此 y = 0⋀1 = 0

  
  

• c(x) = x1：斯蒂文完胜

• 第 3 个 x = [1, 0]，因此 y = 1

• 第 4 个 x = [0, 1]，因此 y = 0

阳春白雪来讲，这个是机器学习中的“无免费午餐” (no free lunch, NFL) 定理，即所有算法，无论高级初级，它们的期望表现相同！下里巴人来讲，一切脱离具体问题来讨论机器学习算法优劣的行为都是耍流氓。

注：NFL 定理的推导见附录 1

现在所有机器学习痴迷者有没有一种冷水浇头的感觉：

 

• 既然胡逼猜和猛炸天的模型期望表现相同，哪还有什么可学的？

• 既便猛炸天比胡逼猜模型表现要好，真实函数 c 是未知的，完美预测样本内数据对预测样本外数据没有什么帮助！只有样本外的表现才是真正的学习，但样本外又是未知的。机器学习是个骗局吗？

如果机器学习没什么可学或是骗局，那就好了，我也不用呕心沥血的研究它了。幸运 (或不幸) 的是，机器学习是可学或可行 (feasible) 的，但是需要从概率的角度来把玩它。

目录

第一章 - 前戏王

    1.1 总体和样本

    1.2 二分类问题

    1.3 对分

    1.4 增长函数

    1.5 打散和突破点

    1.6 联合上界

第二章 - 理论皇

    2.1 学习心路历程

    2.2 从已知到未知

    2.3 从民调到学习

    2.4 从单一到有限

    2.5 从有限到无限

    2.6 从无限到有限

第三章 - 实践王

    3.1 VC 不等式

    3.2 VC 维度

总结和下帖预告

附录

    1 NFL 定理

    2 霍夫丁不等式

    3 增长函数上界

第一章 - 前戏王

1.1

总体和样本

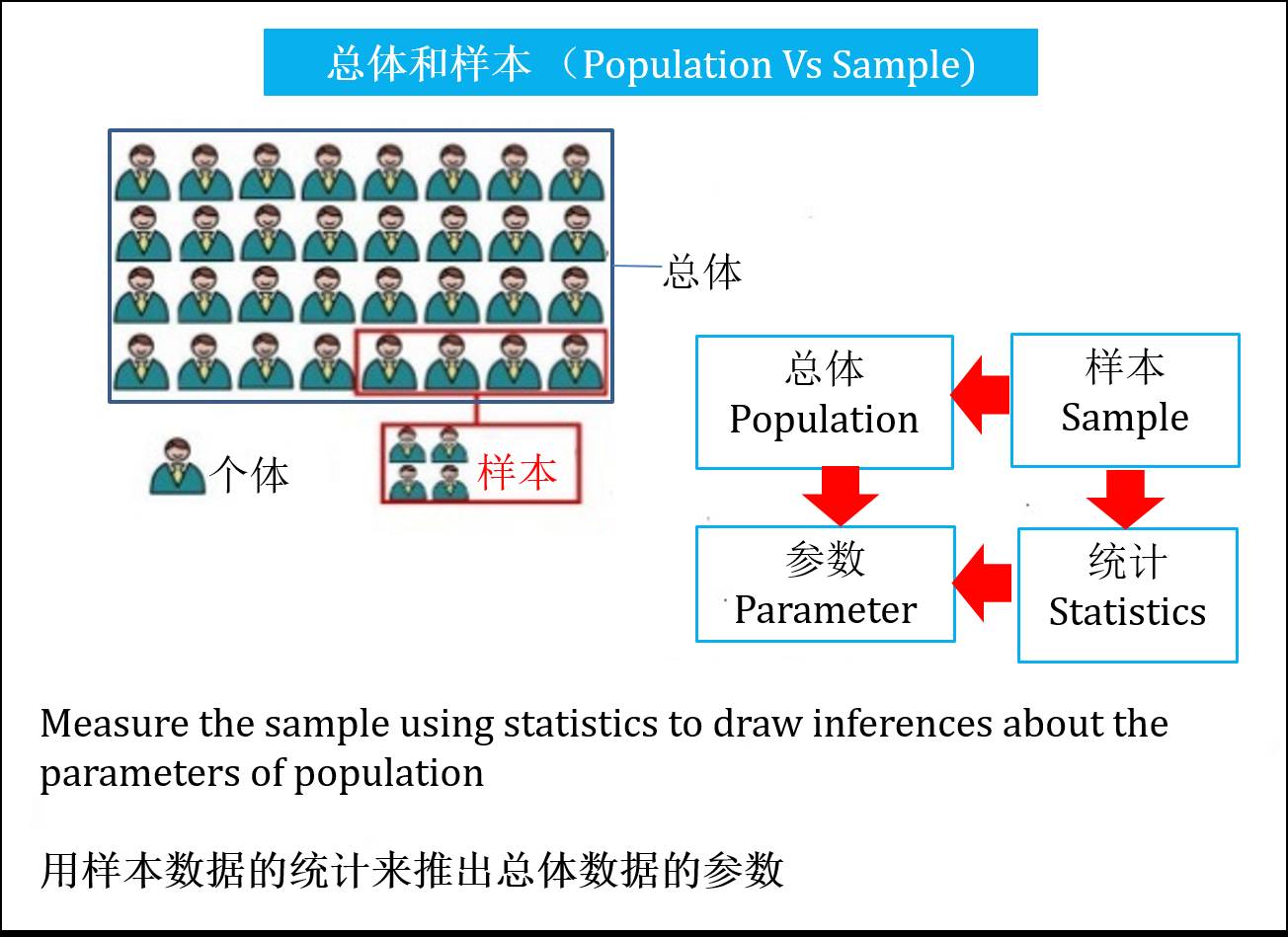
在统计中，把研究对象的全体称为总体，而把组成总体的各个元素称为个体，把从总体中抽取的若干个体称为样本。举个调查中国男性平均身高的例子，全国的男性就是总体，每个男性是个体。有时候普查所有男性金钱花费和时间成本太高，通常我们会抽取若干男性作为样本。我们计算样本里的男性平均身高作为总体里的所有男性平均身高的推理 (inference)。

注：小节 2.2 会用到

1.2

二分类问题

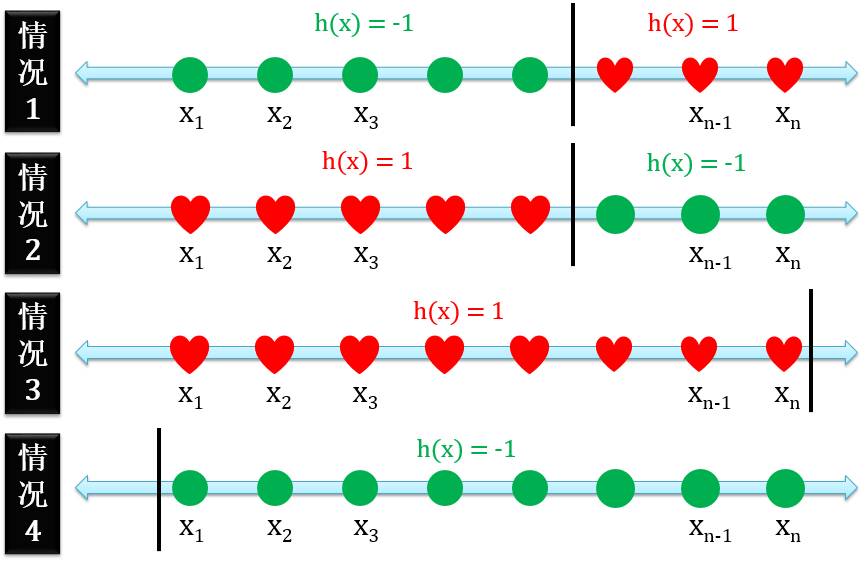
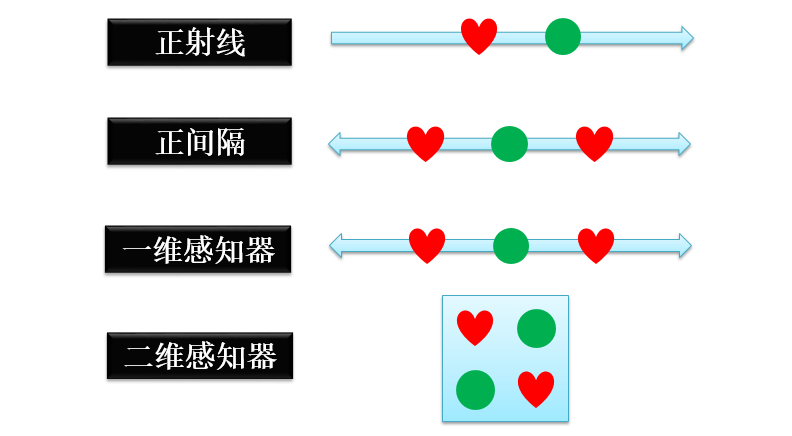
二分类 (binary classification) 问题是将一组数据按照某个规则分为两类。用 h(x) = 1 和 h(x) = -1分别表示正例和反例，具体的几个二分类的例子如下：

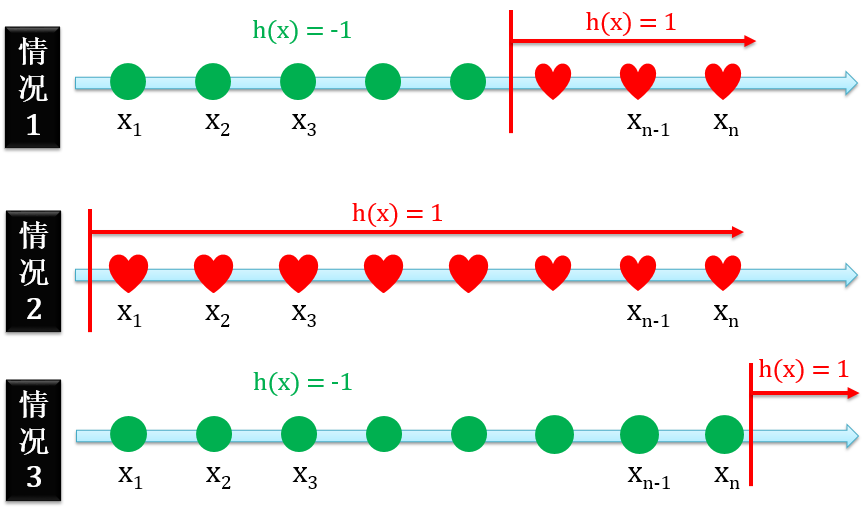
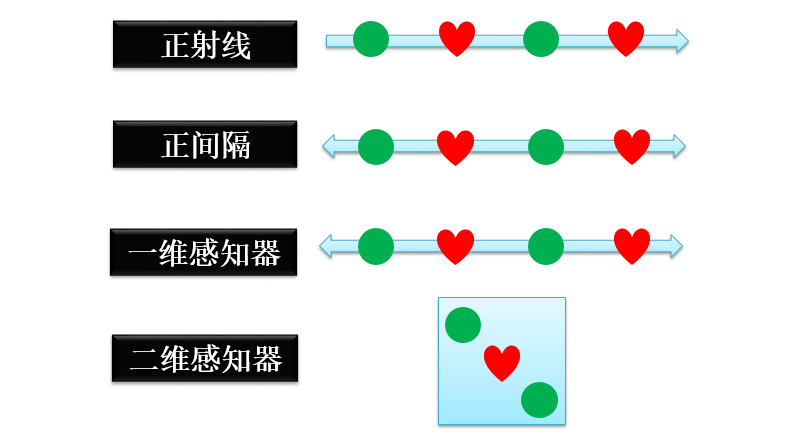
正射线 (Positive Ray)

正射线二分类的定义是在某个点的右边全是正例，有三种情况

1. 正例在反例的右边

2. 只有正例没有反例

3. 只有反例没有正例

下图展示着含 n 个点的正射线：

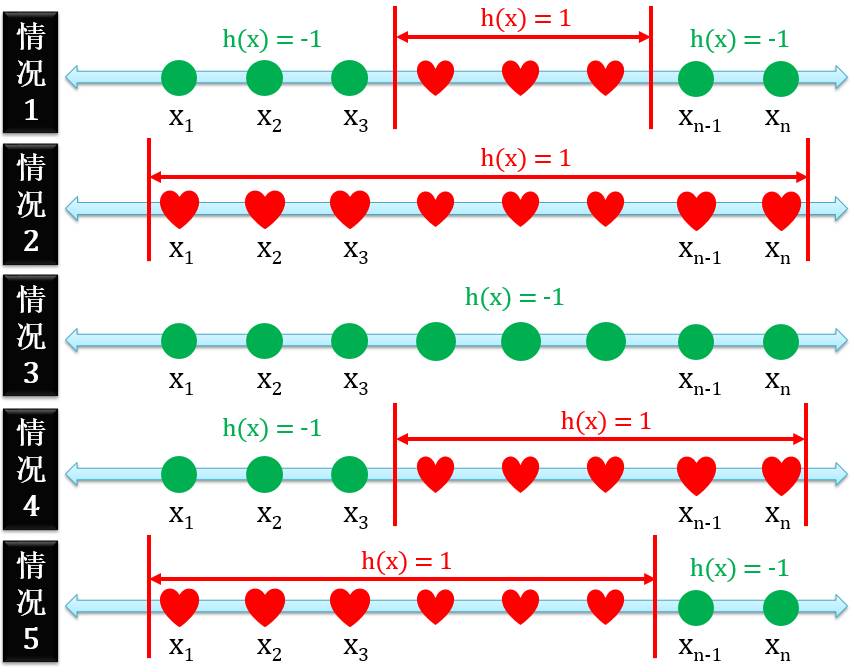
正间隔 (Positive Interval)

正间隔二分类的定义是在某两个点的中间全是正例，有五种情况

1. 正例在反例的中间

2. 只有正例没有反例

3. 只有反例没有正例

4. 正例右边没有反例

5. 正例左边没有反例

下图展示着含 n 个点的正间隔：

一维感知器 (1D Perceptron)

一维感知器就是正射线和负射线的合体，有四种情况

1. 正例在反例的右边

2. 正例在反例的左边

3. 只有正例没有反例

4. 只有反例没有正例

下图展示着含 n 个点的一维感知器：

 

二维感知器 (2D Perceptron)

 

二维感知器就是一维感知器从线升级到面，展示如下：

---

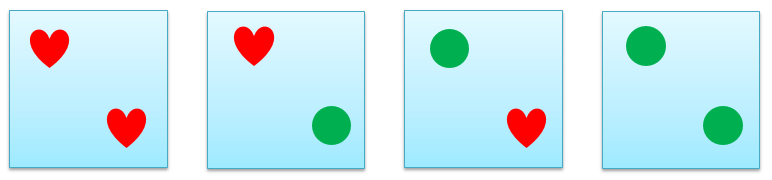
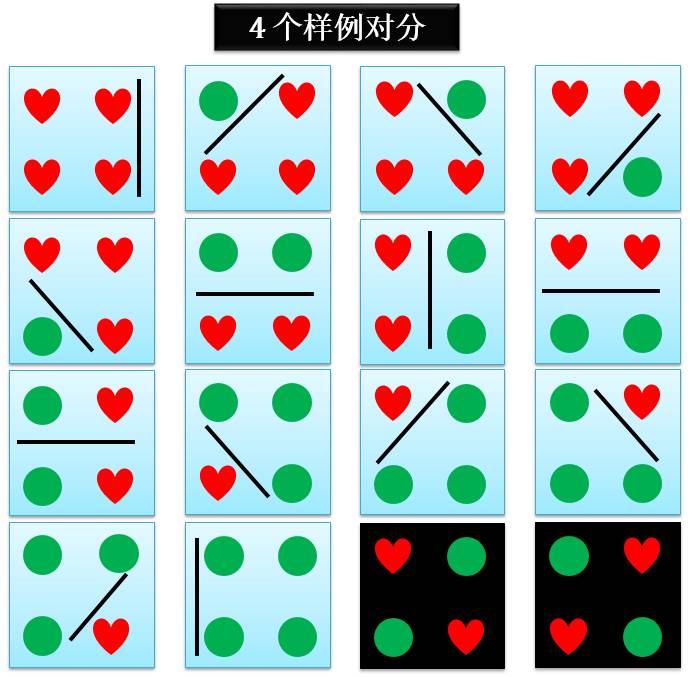
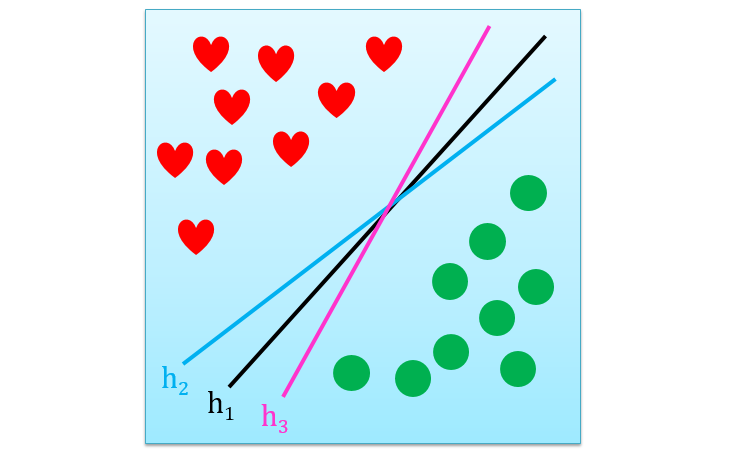
本帖证明机器学习是可行时，仅拿二分类问题为例 (结论对于其他问题也适用)。细心的读者可能看出来，上面举的例子全是红心和绿球正好可以线性分开，但是有些情况是线性不可分的，如下图：

上面四种二分类问题根据它们的定义都不可能用一条线把红心和绿球分开，而我们感兴趣是找到在每个问题下，n 个点被线性对分的结果有多少个。

1.3

对分

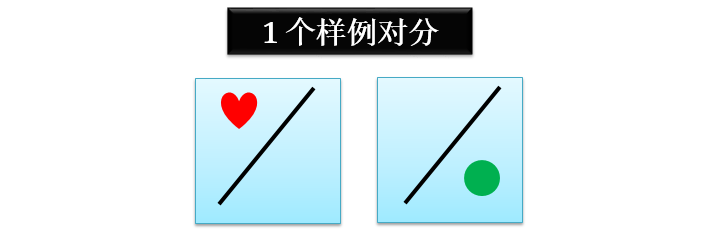
数据集 D 里面有 n 个样例，如果考虑用某种方法给这 n 个样例赋予 2 个标记的话，有 2n 个结果，因为每个样例有 2 种选择，n 个样例就有 2n 选择。用下图举个例子，n = 2，正类为红心，反类为绿球，那么将 2 个点分别赋予红色或绿色，一共有 22 = 4 种结果。

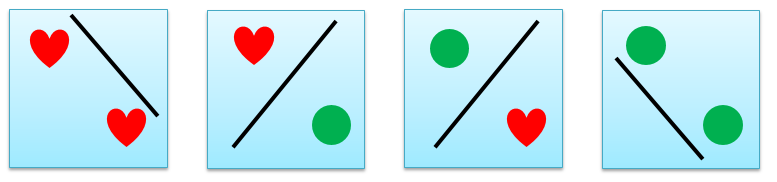
假设经过某种操作 H 是将红心和绿球线性分开，这种分开的操作定义对分 (dichotomy) 。如上图，对分这个操作可以看成是用一条线把红心和绿球分开，如下图所示，2 个点的对分结果一共有 4 种。

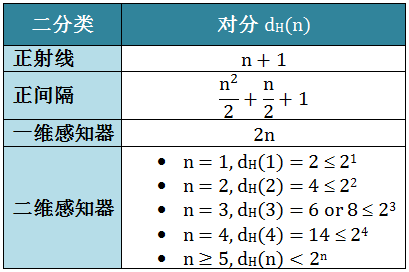
很显然，对于 n 个点，对分的结果最多有 2n 个，但是通常会少于甚至远少于 2n 个。让我们看看上节讲的正射线、正间隔、一维和二维感知器的对分有多少个，对分个数定义为 dH(n)，其中

    H 是某种对分的操作

    n 是数据点的个数

正射线 (Positive Ray)

上图 n 个紫色的点可被 n+1 条虚线划分，对于每条虚线，把其右边所有紫点变成红心，把其左边所有紫点变成绿球。因此正射线的对分

    dH(n) = n+1 ≪ 2n

正间隔 (Positive Interval)

在 n+1 条虚线中任取 2 条，把其中间所有紫点变成红心，而其他紫点变成绿球，这总共有 0.5n(n+1) 种；此外加上一种全是绿球的结果，因此正间隔的对分

    dH(n) = 0.5n2+0.5n+1 ≪ 2n

一维感知器 (1D Perceptron)

上图 n 个紫色的点可被 n-1 条虚线划分，对于每条虚线，把其右边 (或左边) 所有紫点变成红心，把其左边 (或右边) 所有紫点变成绿球；此外加上两种全是红心或绿球的结果。因此一维感知器的对分

    dH(n) = 2(n-1)+2 = 2n ≪ 2n

二维感知器 (2D Perceptron)

二维感知器的对分情况比较复杂，要按着样例的个数来讨论。

---

当 n = 1 时，对分情况只可能是下图所示的 2 种情况：

因此 1 个样例的二维感知器的对分

    dH(1) = 2 = 21

---

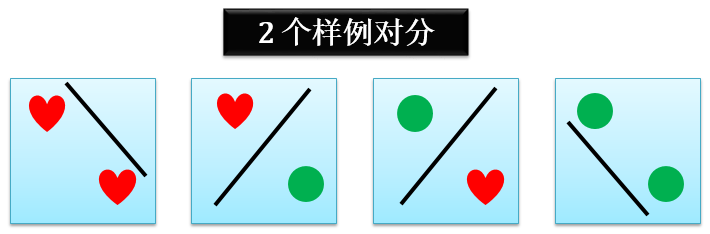
当 n = 2 时，对分情况只可能是下图所示的 4 种情况：

因此 2 个样例的二维感知器的对分

    dH(2) = 4 = 22

---

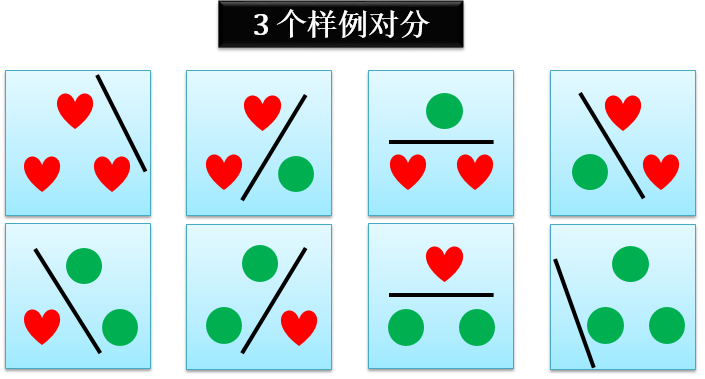
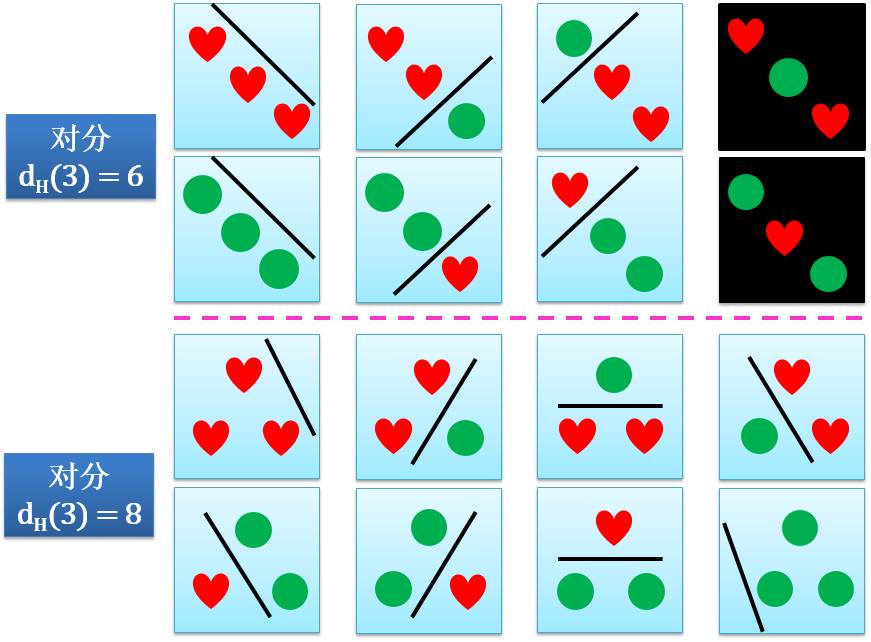
当 n = 3 时，一种对分情况是下图所示的 8 种情况：

在这种情况下 3 个样例的二维感知器的对分

    dH(3) = 8 = 23

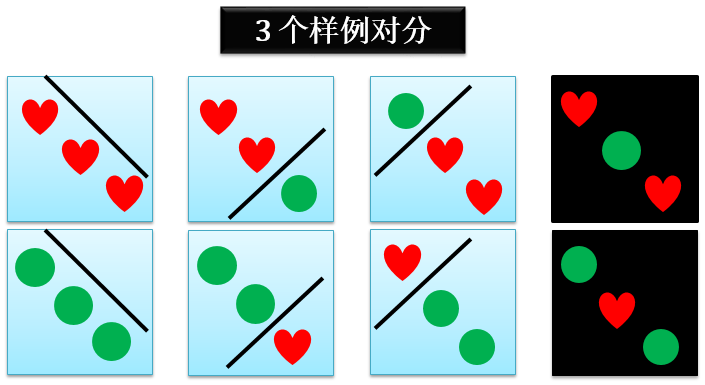
但是，还有别的情况吗？下图给你答案：

在这种情况下 3 个样例的二维感知器的对分只有 6 个。看看那两个黑色高亮图，你能用一条线将红心和绿球分开吗？在这种情况下 3 个样例的二维感知器的对分

    dH(3) = 6 < 23

综上，3 个样例的二维感知器的对分可能为 6，也可能为 8。

---

当 n = 4 时，对分情况只可能是下图所示的 14 种情况：

因此 4 个样例的二维感知器的对分

    dH(4) = 14 < 24 

当 n ≥ 5 时，二维感知器的对分情况也越来越复杂，但是根据上面 n = 1,2,3,4 的结果，大家可以猜测

    dH(n) < 2n

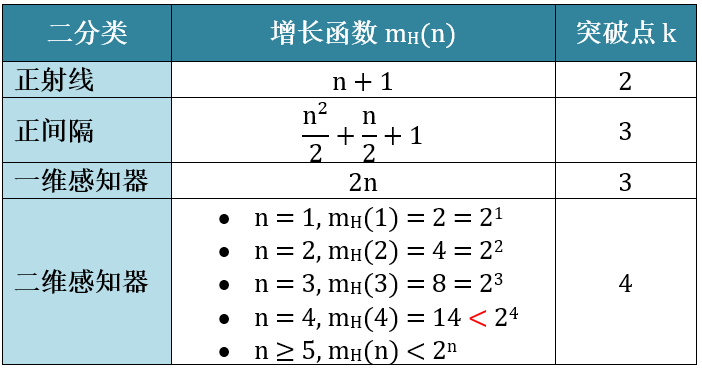
最后各种二分类的对分总结于下表：

1.4

增长函数

由于对分个数在固定 n 点的情况下可能有多个值，比如二维感知器的 3 个点的情况下，dH(3) = 6 或者 8，根据这 3 个点不同的分布情况，如下图所示：

对分运用起来有一点麻烦，因为它不仅和点的个数 n 有关，还和点的分布情况有关。我们希望定义一个只和 n 有关的量，增长函数 (growth function)，它取每个 n 点对分时的最大值。

    mH(n) = max( dH(n) )      

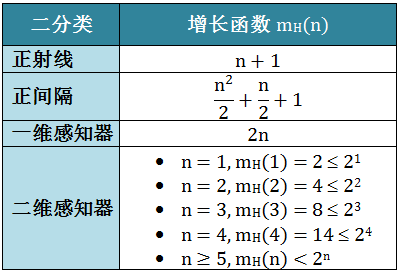
增长函数值越大则这个操作 H 的表示能力越强 (后来我们把这个操作 H 定义成机器学习的假想空间 H)，复杂度也越高，学习任务的适应能力越强。最后各种二分类的增长函数总结于下表：

注：小节 2.5 会用到

1.5

打散和突破点

假设经过某种操作 H 能实现数据集 D 上所有的对分，则称数据集 D 能被这个操作 H 打散 (shatter)。既然能实现所有对分，那么打散时对应的增长函数为 2n。下图就是一个 2 个样例打散的简单例子，实现了所有对分，增长函数为 22 = 4。

打散这个概念固然重要，但是认识到不打散更加重要。把第一个没被打散对应的 k 点称为突破点 (break point)。

下图展示各种二分类问题没被打散的情况：

 

• 正射线：在此二分类怎么样都不能打散 2 个点，因为在正射线定义下红心一定要在绿球右边，这样突破点 k = 2。

• 正间隔：在此二分类怎么样都不能打散 3 个点，因为在正间隔定义下红心一定要在绿球中间，这样突破点 k = 3。

• 一维感知器：在此二分类怎么样都不能打散 3 个点，因为在红心或绿球一定要连在一起，这样突破点 k = 3。

• 二维感知器：在此二分类怎么样都不能打散 4 个点，这样突破点 k = 4。

大家可能会想了，对于二维感知器，不是有一种 3 个点的情况也不能被打散吗？但是也有一种 3 个点的情况可以被打散啊，这就足够了。只要一种情况可以打散就够了。而 4 个点是各种情况都不能被打散，因此突破点是 4。

各种二分类的突破点总结于下表：

从上表 (正射线、正间隔、一维感知器) 观察出增长函数 mH(n) 是 n 的多项式，而它的最高阶小于突破点 k 减 1，比如

 

• 正射线 mH(n) 是 1 阶多项式，而突破点 k 是 2，k – 1 = 1

• 正间隔 mH(n)是 2 阶多项式，而突破点 k 是 3，k – 1 = 2

• 一维感知器 mH(n) 是 1 阶多项式，而突破点 k 是 3，k – 1 = 2 ≥ 1

但是二维感知器 mH(n)也是 k-1 阶多项式吗？

注：小节 2.5 会用到

1.6

联合上界

假设 A1, A2,…, Ak 是 k 个不同的事件 (他们不一定相互独立)，那么

通常上式当成一个公理来用而无需证明，它所表达的意思也非常直观，k 个事件中任何一个事件发生的概率最多就是 k 个事件发生概率的和。

注：小节2.4会用到

第二章 - 理论皇

2.1

学习心路历程

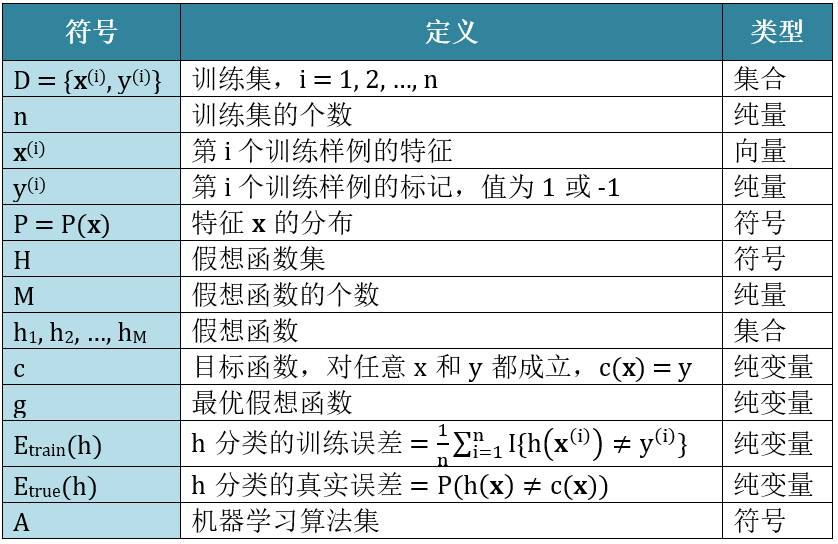
首先，列出全文需要用的符号：

从引言的两个疑惑开始：

1. 既然胡逼猜和猛炸天的模型期望表现相同 (天下无免费午餐，NFL 定理)，哪还有什么可学的？

2. 既便猛炸天比胡逼猜模型表现要好，目标函数 c 是未知的，完美预测样本内数据对预测样本外数据没有什么帮助！只有样本外的表现好才能说机器真正学习到了目标函数 c，但样本外又是未知的。机器学习是个骗局吗？

对于第一个疑惑好解释，NFL 定理的假设是：所有问题出现的机会相同，即所有目标函数 c 发生的可能性是均匀分布的 (从附录 1 可知)。但是实际上并不是这样的，某些时候某个 c 发生的可能性大，或某种问题出现的机会更大。比如某个问题中一组数据呈现明显的线性关系，那么目标函数 c 为线性函数的可能性最大，而 c 为 10 阶多项式的可能性几乎为零。由此可知每一个具体问题都有一个最有可能的目标函数 c 以及一个最优的算法，脱离具体问题空谈算法毫无意义。

对于第二个解惑：学习的最终目的就是找到这样一个未知的目标函数 c，因为它可以将任意数据都能正确分类，但是这不可能的，因为任意数据里面包括你还没有见过的数据，数据都是未知的，你如何能学习到作用到它上面的目标函数 c？

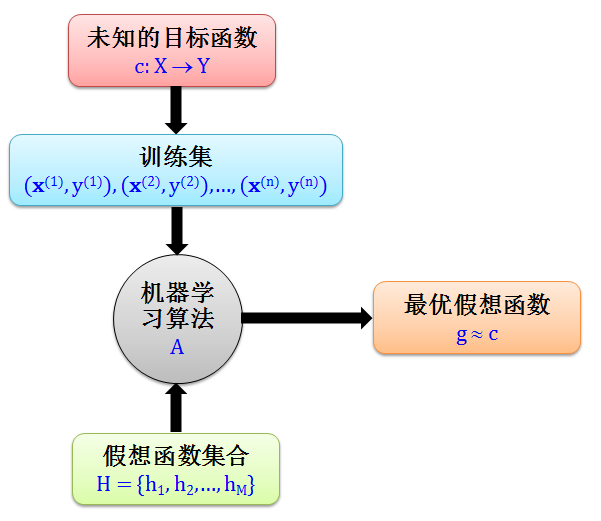
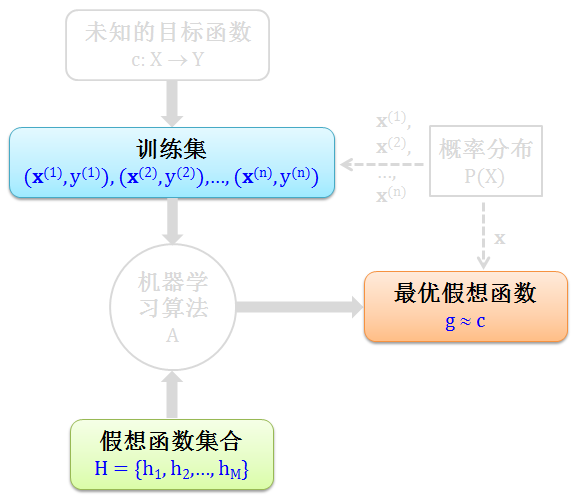
那我们就退一步，既然找不到 c，我们来找它的影子 g。这个 g 函数是从假想函数集合 H 中，用机器算法得出的最优假想函数。既然 g 是 c 的影子，那么 g ≈ c。这套做法听起来还算合理，下图清晰的画出了其流程。

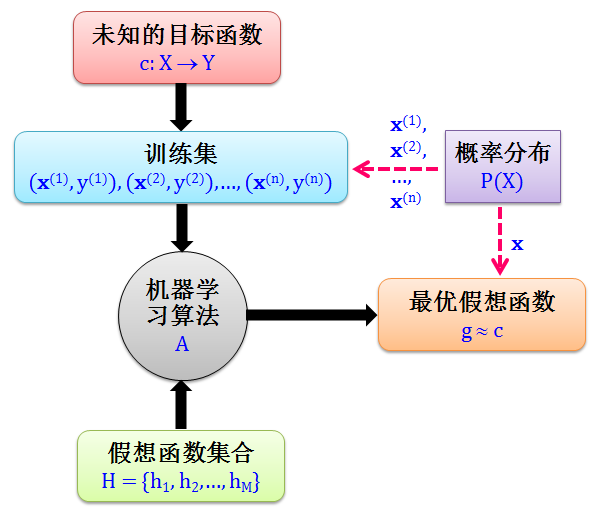
这里有一个非常重要的假设，即“所有数据的特征 x 都是来自一个概率分布 P，而 P 可以是未知的”。如果这个假设不成立，机器学习根本进行不下去，试想你从一个训练集 (x 服从正态分布) 学习到一个模型在测试集 (x 却服从泊松分布) 做分类，模型表现好坏没有任何参考价值。下图在上图基础上加上了概率分布 P，其流程如下：

到现在已经有一个机器学习的框架了，目标很明确就是找一个g ≈ c，如果找得到 g 那么机器学习可行，找不到 g 那么机器学习不可行。因此要证明机器学习可行，我们需要完成下面的逻辑链

    证明机器学习可行

=>

    学习到目标函数 c

=>

    间接找到 g 来最小化真实误差

现在问题来了：

• 目标函数 c 是未知的

• 真实误差 Etrue(g) 无法计算

上面证明“机器学习可行”还能继续吗？先别急，想想目前你能够做到什么：你有能力做到最小化训练误差 Etrain(g)，加点以下巧思：

 

    Etrain(g) ≈ Etrue(g)  

    Etrain(g) 很小

=>

    Etrue(g) 很小

=>

    g ≈ c

=>

    机器学习可行

 

如果我们能

 

• 证明在某种条件下 Etrain(g) ≈ Etrue(g) [上天眷顾]

• 使用不同算法使得训练误差 Etrain(g) 很小 [个人实力]

那么真实误差 Etrue(g) 也很小。机器学习是可行的。上天是眷顾机器学习者的，本章后面霍夫丁会告诉你 Etrain(g) ≈ Etrue(g) ；至于个人实力来最小化训练误差 Etrain(g)，你只有努力学习各种算法了。至少你有了上天眷顾，有了理论的支持，有了强大的自信，可以静心专研算法了。

本章之后小节内容如下：

1. 小节 2.2 从已知推未知：以美国大选民意调查为例，用霍夫丁不等式来证明如何用民调得到希拉里支持率推测出全体选民支持希拉里的概率

2. 小节 2.3 从民调到学习：将民意调查转化成双色球游戏，将双色球游戏又类比在机器学习上，用霍夫丁不等式来证明在一个假想函数的情况下如何用样本内误差 (训练误差) 推测出样本外误差 (真实误差)

3. 小节 2.4 从单一到有限：用一个假想函数并从训练误差推测出真实误差不叫学习，顶多叫验证；用霍夫丁不等式来证明从有限多假想函数中选取最优假想并从训练误差推测出真实误差才叫学习

4. 小节 2.5 从有限到无限：假想函数通常是无限多个，霍夫丁不等式能不能证明从无限多假想函数中选取最优假想并从训练误差推测出真实误差

5. 小节 2.6 从无限到有限：通过增长函数和突破点等概念，用霍夫丁不等式来证明从无限多假想函数中选取最优假想并从训练误差推测出真实误差

2.2

从已知到未知

让我们看看美国大选民意调查的例子。民调的方法很简单，用的就是最基本的统计采样的理论。比如在加州做民调，从加州全部选民中随机挑选一批选民，记录他们得投票倾向，综合起来就得到加州选民的意向了。

 

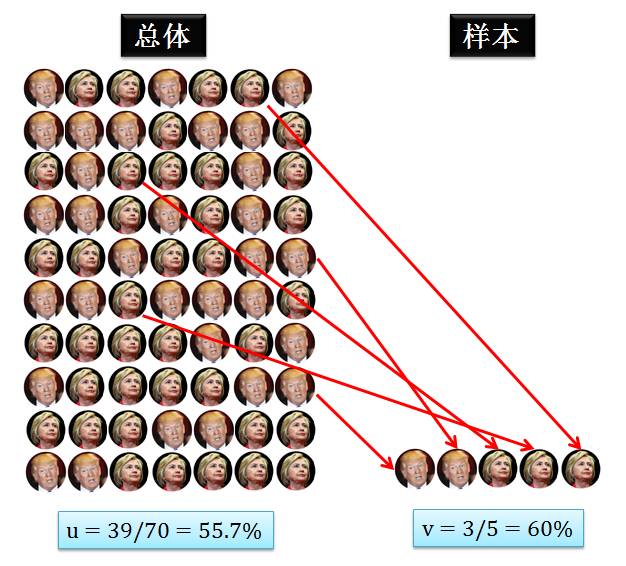
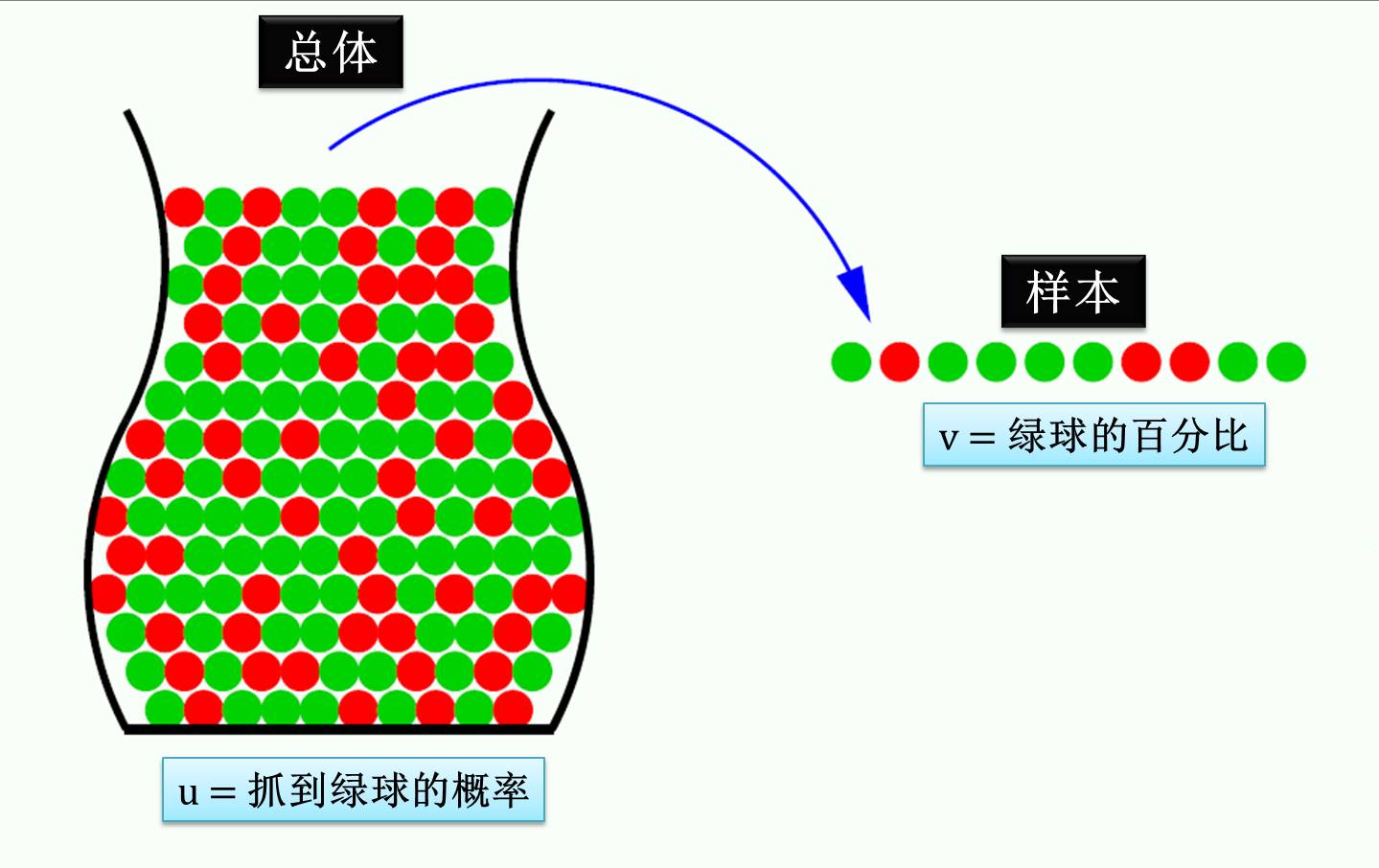
当希拉里和川普胶着时，随便问问一个加州人，比如科比，你只能得到一边倒的结论，但当你问了上万人的时候，平均起来的结果就相当准了。上面这个陈述可以说概率近似正确 (probably approximately correct, PAC)。很绕口是不是？听我慢慢讲来，先看下图。

• 上图左边展示着总体，希拉里头像代表着加州全部选民中的一个支持希拉里，而川普头像代表着加州全部选民中的一个支持川普。因此总体中希拉里头像的个数除以总头像个数就是希拉里的真实支持率，我们用 u 来表示，它是个未知量 (因为加州人数太多，计算它的值太费人力财力) 但是确定量 (它的值不会变，就客观存在于全体选民的结果中)。
  

• 上图右边展示着样本，可以把它理解成民调的结果，从总体随机选出选民得知她的支持对象并记录下。因此样本中希拉里头像的个数除以总头像个数就是希拉里的调查支持率，我们用 v 来表示，它是个已知量 (样本人数少，可以计算出它的值) 但是随机量 (它的值随着每次民调采样不同而变化)。

通过民调之后，我们计算出分数 v，但是通过了解 v 对了解 u 有帮助吗？

斯蒂文

没有！虽然大多数选民都选希拉里 (u 很大)，但是民调的那些选民可能都选川普 (v 很大)，v 和 u 没毛关系

霍夫丁

你说的这种情况是可能的 (possible)，但不是很有可能的 (probable)。在样本足够多时，v » u 概率近似正确 (PAC)

你看，这就是斯蒂文和霍夫丁的差距。斯蒂文自作聪明以为举了一个反例就能推翻“从样本 v 不能推断总体 u ”这个结论；而大师霍夫丁高逼格的从 PAC 上做文章，称“当样本数足够大，v 和 u 就足够靠近”，并且还给出严谨的数学公式来证明。

霍夫丁不等式 (Hoeffding’s inqeuality) 就量化了 v 和 u 之间的关系。

其中

    ε 是任意正数

    n 是样本个数

    |v - u| > ε 指的是 v 和 u 之间相差 ε

    P 是事件 |v - u| > ε 概率

注：霍夫丁不等式的推导见附录 2

上面两个不等式是等价的，通常我们用第一个不等式。首先不要被它吓住了，其实这个公式表达的意思很直观：如果一开始选一个很小的 ε (言外之意是目的是想让 v 和 u 值接近)，那么为了让不等式右边 2exp(-2ε2n) 很小，只能调大 n 值。

 

举个实际例子，如果你希望希拉里真实支持率 v 和民调支持率 u 相差不超过0.02(2%)，那么调查 5000 个人(n = 5000)，算出 1-2exp(-2ε2n) = 0.9816，换句话说就是 98% 的时间里，

 

    v – 0.02 ≤ u ≤ v + 0.02

 

这个时候，你如果用 v 值来代替 u 值，98% 的情况下是没问题的。

 

上面公式和例子转成白话文就是

 

    如果 n 很大，v ≈ u 的概率接近

 

或者说 v ≈ u 在概率上近似正确。这样我们易计算的 v 是难计算的 u 的一个很好的逼近。这个不等式更牛的地方是右边的概率上界 2exp(-2ε2n) 完全和 u 无关，而且 n 是样本大小不是总体大小，这个上界完全把自己和总体 (未知的东西) 脱得一干二净。是的！不管总体个数是多少，不管总体变量有多么未知，给我一个 n，我就能计算一个“已知到未知”的概率上界。

 

到现在，我们走完了“从已知推未知”的这一步，我们学习到了一些事情，比如通过 v 学习到了 u。

 

小节要点：

1. 霍夫丁不等式成立的条件是取样的个体是独立同分布的

2. 霍夫丁不等式是连接已知和未知的纽带

2.3

从民调到学习

民调的做法弄清楚了，可我们现在讲的是机器学习啊。没关系，做一下类比发现两者的实质是一样的，这样我们就可以把用在民调的那一套用在机器学习上。

首先我们把民调想成是一个从双色球的问题，其中

• 每一个球代表民意调查里面的一个选民

• 如果此选民支持希拉里，将球涂成绿色

• 如果此选民支持川普，将球涂成红色

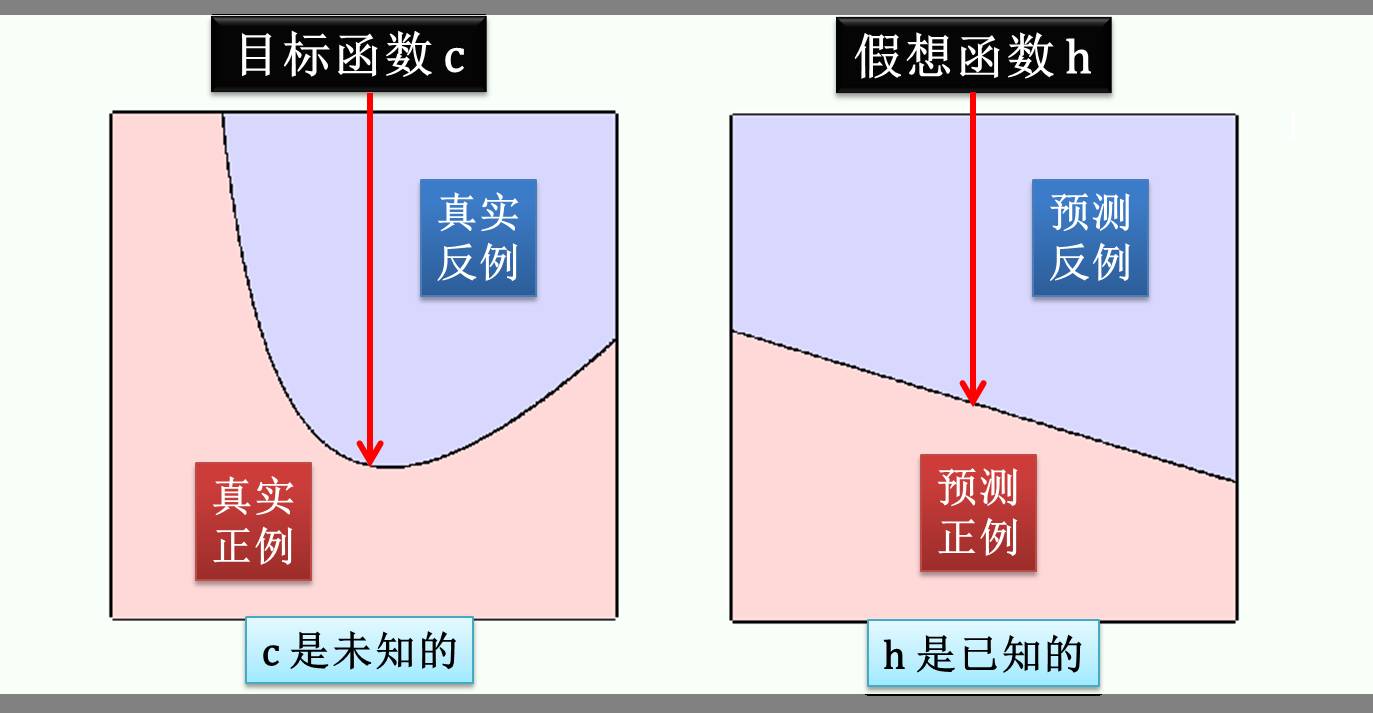
接着再看一个二分类问题，用一个函数 h 将正例和反例分开，h 越接近目标函数 c 越好：

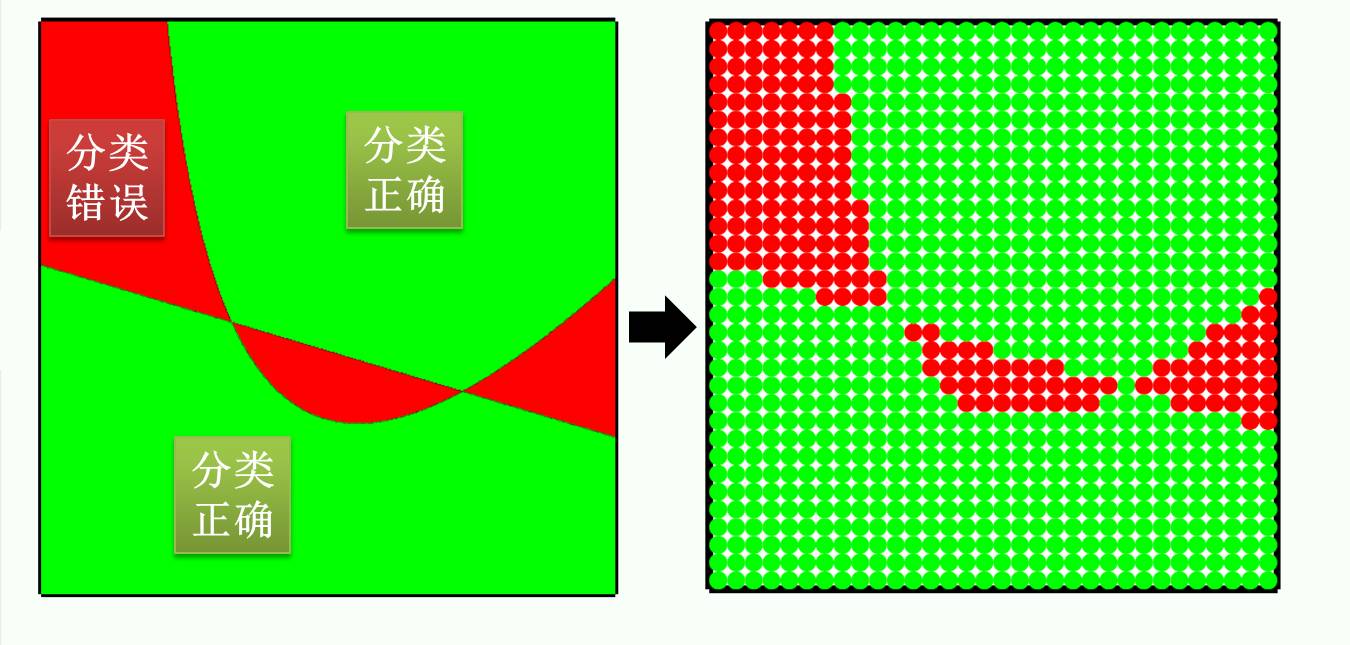
但是 c 是未知的，用 h 来逼近 c 来分类肯定会有些错误，下图绿色部分代表分类正确 h(x) = c(x)，而红色部分代表分类错误 h(x) ≠ c(x)。(虽然 c 是未知的，但是它是存在的，因此图中的 c 只是一种可能)

上图左边到右边将一个二分类问题巧妙的转成一个双色球问题，其中

• 每一个球代表机器学习里面的一个数据

• 如果这个数据分类正确，将球涂成绿色

• 如果这个数据分类错误，将球涂成红色

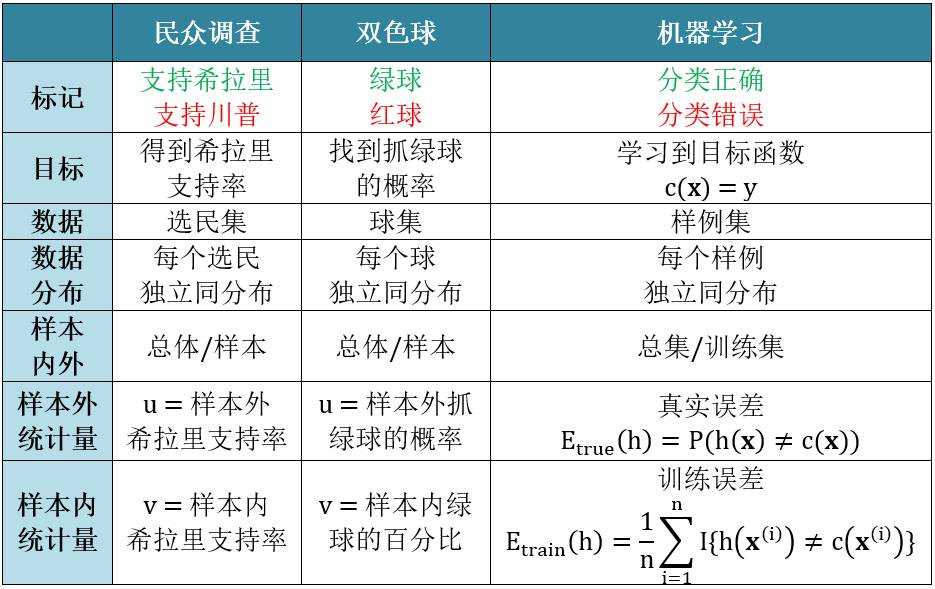
现在已经成功把民意调查和机器学习用双色球来描述，接着做进一步的类比：

根据上节用霍夫丁不等式为民意调查证出的定理，用上表的类比将 u, v 用 Etrue(h), Etrain(h) 替换得到机器学习的定理

上面不等式

• 对所有 n 和 ε 都成立

• 和 Etrue(h) 无关，因此目标函数 c 仍然可以保持未知

• Etrue(h) ≈ Etrain(h) 概率上近似正确 (PAC)

 

换一句更振奋人心的话，当数据足够多 (n 足够大) 时，训练误差和真实误差差别非常小 (ε 很小)，只要你找到好的算法使得训练误差很小，那么真实误差也就很小。

 

如果更通俗把“h 的训练误差和真实误差差别大”想成“坏h”，因为这种情况我们无法通过很小“h的训练误差”来推出很小“h的真实误差”。那么将上面机器学习版本的霍夫丁不等式写成

为了证明学习是可行的，我们希望证明 h 不是坏的，那么证明 P(坏h) 很小，那么证明 2exp(-2ε2n) 很小。好像增大 n 都可以证明一切哦？难道我们已经证完了学习是可行的？

小节要点：

 

1. 通过类比推出了机器学习版本的霍夫丁不等式，连接上了训练误差和真实误差

2. 给定一个假想函数 h，霍夫丁不等式证明了当 n 足够大，h的训练误差 ≈ h的真实误差。

2.4

从单一到有限

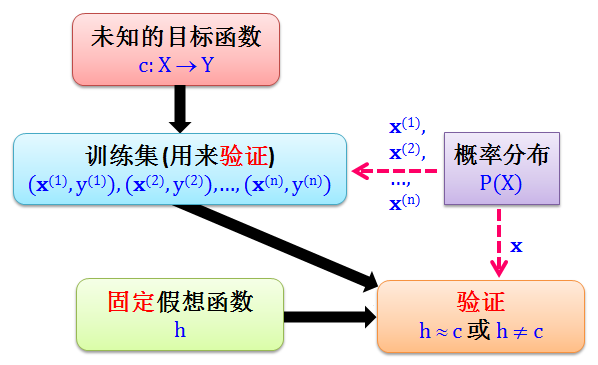
上节的结论只用了一个固定的假想h，而不是一组假想 h1, h2, …, hM，机器没有学习 (learn) 到任何东西，充其量只能说验证 (verify)了一个东西，就是这个固定 h 和目标函数 c 的差距，有两种验证情况 (现在已经知道 Etrue(h) ≈ Etrain(h) 而 Etrue(c) = 0 )：

 

1. 如果 Etrue(h) ≈ 0，那么 Etrain(h) ≈ 0，h 学到了 c，因为用 h 来预测的真实误差接近于 0，就是 h 都预测准了

2. 如果 Etrue(h) ≫ 0，那么 Etrain(h)≫ 0，h 没学到 c，因为用 h 来预测的真实误差远大于 0，就是 h 都预测不准

 

但如果 Etrue(h) ≈ 1，那么 Etrain(h) ≈ 1，h 完全没学到c，但是每次和 h 的预测反着来就能学到 c。由此可见当 Etrue(h) = 0.5 时是最坏的情况，但是这种情况我们无法控制，因为当我们只有一个 h 时，我们无法控制它的训练误差 (它就客观存在)。

 

上述验证过程的流程图如下：

和小节 2.1 学习过程的流程图相比，不同之处在于：把 h 用到训练集上计算训练误差，如果很小那么我们验证出 h 学到了 c，如果很大那么我们验证出 h 没学到 c。记住，这和学习无关！

现在问题集中到如何有一个机制使得 Etrain(h) ≈ 0。简单，从一组假想函数 h1, h2, …, hM 中选出一个使得 Etrain(h) 最小，并将这个最优假想函数设定为 g，只要满足

那么 Etrue(h) ≈ 0，g 真的学到了 c。上面不等式成立吗？成立 -- 霍夫丁。

以上证明

• 第二行从数学公式转换成通俗说法

• 第三行说 g 如果是坏的，因为 g 是从一堆 h 中选出的，那么至少有一个 h 是坏的

• 第四行利用 1.6 节的联合上界

• 第五行将霍夫丁不等式用在每一个 hm 上

• 最后一行简单加总

从 h 升级到 g，唯一改变就是右边多出一个 M (假想函数的个数)

为了证明学习是可行的，我们希望证明 g 不是坏的，那么证明 P(坏g) 很小，那么证明 2Mexp(-2ε2n) 很小。好像增大 n 都可以证明一切哦？现在我们应该证完了学习是可行了吧。

 

小节要点：给定一组假想函数 h1, h2, …, hM 选出一个最优假想 g，霍夫丁不等式证明了当 n 足够大，g的训练误差 ≈ g的真实误差。

2.5

从有限到无限

在实际问题中，假想个数 M 真的是有限的？来，看看下面的图

图上所有黑线都可以将红心和绿球线性分开，但是这种黑线有无数条。假如每一条黑线对应着一个假想函数，那么 M 是正无穷。带入上节证出的不等式看看

即便增大 n，当 M 是正无穷时，我们只能证出“P(坏g) ≤ 很大的数”，恭喜你，一个小学生都知道“P(坏g) ≤ 1”，比你还进一步呢。问题出在哪儿呢？

2.6

从无限到有限

问题出在坏事情是相互重合的，坏 h1 和坏 h2 可能基本就一样，而用 1.6 节的联合上界使得上界太过于松，也就是下面不等式右边太过于大

既然找到了问题根源，现在就要解决实际问题，看是否能从无限的 M 变成一个有限值。答案是可以的，但首先来介绍以下等效假想，如下图所示：

上面假想 h1, h2 和 h3 都是等效的，无限多的假想就这样被归结为等效的一类，而增长函数 (见小节1.4) mH(n) 就是计量这等效的类数的。但是增长函数的上界是 2n，用 mH(n) 来替代上面不等式里的 M 得到

从倒数第二步得知，分子分母都可写成 ecn 的形式，这样它们等阶无穷大 (就是当 n 趋近无穷大时，分子分母趋近无穷大的速率一样)，因为 ln2 通常会比 2ε2大，因此最后结果会比 1 大。恭喜你，一个小学生还是知道“P(坏g) ≤ 1”，比你还是进一步。问题就出在增长函数的上界 2n 太过于大，而不能使得当 n 很大时不等式右边是一个很小的值。如果我们能找到 mH(n) 是 exp(2ε2n) 的低阶无穷大就好了(就是当 n 趋近无穷大时，分母趋近无穷大的速率比分子快)。还记得小节 1.5 最后对 mH(n) 是多项式的猜测吗？多项式函数的确是指数函数的低阶无穷大，如果猜测成立，我们所有证明就全部成立了。

 

事实上，增长函数的确有一个更小的上界，那就是多项式

注：增长函数上界的推导见附录3

 

这时再来看看“坏g”的概率是否能被限制在一个很小的数下

最后一步是由洛比达法则得到，将 k-1 阶多项式函数和指数函数分别求 k-1 次导数后，分子为常数而分母还是和 n 相关的指数函数，这样当 n 很大时，整个商会很小。返回严谨的数学公式，现在我们已经得到

再回到小节 2.1 证明学习可行两个必要条件

• 证明在某种条件下 Etrue(h) ≈ Etrain(h) [上式已证]

• 使用不同算法使得训练误差 Etrain(h) 很小 [看你造化]

我们可知 Etrue(h) 很小，那么训练出来的模型真的能用来预测。

第三章 - 实践狼

3.1

VC 不等式

小节 2.6 最后证出的不等式就是大名鼎鼎的 Vapnik-Chervonenkis (VC) 不等式的仿真版，真正的 VC 不等式有几个系数要修改

上图红色和蓝色符号显示出仿真版和真正的 VC 不等式的不同之处，完整的证出那些蓝色符号需要很多的专业知识，感兴趣的同学可参考：

https://www.csie.ntu.edu.tw/~htlin/course/ml08fall/doc/vc_proof.pdf

不等式右边的项称为 VC 上界，就是它让真实误差偏离预测误差的概率变得足够小，当样本数 n 足够大。

3.2

VC 维度

VC维度和突破点

给定数据集 D 有 n 个点和假想函数空间 H，回忆一下打散和突破点的定义 (见小节 1.5)：

• 打散是 n 个点能被 H 实现所有对分

• 突破点是第一个无法被打散的点，记做 k

既然 k 是第一个无法被打散的点，那么 k-1 一定是最后被打散的点，而通常把它定义成 VC 维度 (VC dimension)，有

    dvc = k – 1

把 VC 维度带入 VC 不等式 (将 dvc 替代 k-1) 得到

只要 dvc 是有限的，那么当 n 很大时，不等式最右边都是一个很小的数，则真实误差 Etrue(g) 逼近训练误差 Etrain(g)，那么假想函数 g 有很好的泛化能力。更重要的是，得到以上结论是

• 不需要知道算法 (algorithm A)

• 不需要知道数据分布 (input distribution P(X))

• 不需要知道目标函数 (target function c)

我们只需要训练集 (training set D) 和假想函数集 (hypothesis set H) 就能找到最优假想函数 g 来学习 c，如下图所示：

模型复杂度

 

设定一个概率 δ，计算样本数 n 和容忍度 ε 之间的关系

因此在大于 1-δ 的概率下

上式最后引进了惩罚函数 Ω，也称模型复杂度 (model complexity)。这个参数描述的意义是，假设空间 H 越强，我们的算法在泛化能力上越需要付出多少代价。通俗的来讲，H 容量越大，VC 维度越大，那么模型就越难学习。当

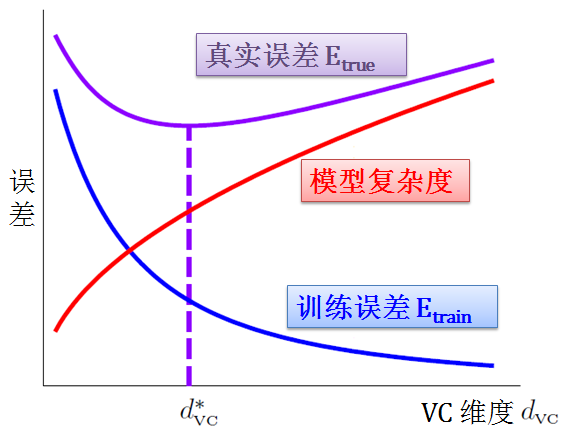
• dvc 增大：Etrain 减小 (模型越复杂越易解释训练集) 但是 Ω 增大 (是 dvc 的增函数)

• dvc 减小：Etrain 增大 (模型越简单越难解释训练集) 但是 Ω 减小 (是 dvc 的减函数)

VC 维度是模型复杂度的增函数，但是不是 Etrue 的增函数。VC 维度越大或者假设空间能力越强大，虽然可以使得训练误差很小，但不见得是最好的选择，因为要为模型复杂度付出代价。机器学习的任务就是找到一个最佳 d*vc 来找到一个最小 Etrue，如下图所示：

样本复杂度

 

你还可以设定想要的容忍度 ε，看看需要多少样本数 n 能实现它，也就是说计算出样本复杂度 (sample complexity)

虽然解出了 n，但上式左右两边都含 n，因此需要用迭代方法 (如牛顿法) 解出，比如设定

 

• ε = 0.1，希望 Etrue(g) 和 Etrain(g) 之间不要超过 0.1

• δ = 0.1，有 90% 的可能上述情况会发生

 

经过迭代法算出

• 当 dvc = 3，n ≈ 30000

• 当 dvc = 4，n ≈ 40000

• 当 dvc = 5，n ≈ 50000

 

因此理论上来讲，n ≈ 10000dvc，但是从实践上来讲 n ≈ 10dvc。为什么需要样本数量可以从 10000 倍减到 10 倍呢？原因是上面推出的 VC 上界是很松 (loose) 的，因为在推导时，我们用的

 

• 霍夫丁不等式适用于任何数据分布和任何目标函数

• 增长函数适用于任何数据

• VC 维度适用于任何假想空间

• 联合上界适用于最差的状况

 

上面红色字眼充满着各种“任何”和“最差”，但在实践时，这些都不太可能同时发生，这使得在样本复杂度的估计上实际值可以和理论值相差很大。

总结和下贴预告

经过这一贴异常艰难的讲解，我们得出结论– 学习是可行的。

 

首先，NFL 定理让我们认识到脱离具体问题而空谈算法优劣毫无意义。然后用霍夫丁不等式结合增长函数和突破点证明出当数据足够多时，最优假想 g 的训练误差会和 g 的真实误差很接近。如果 g 能使训练误差很小，那么我们有理论支持 g 的真实误差也很小。因此 g 学到未知的目标函数 c，机器学习是可行的。

 

再总结一下要学到有用的东西需要的几个条件：

 

1. 好的假设空间 (good hypothesis space)：存在突破点，使得训练误差和真实误差能够接近

2. 好的数据  (good data)：数据足够多，使得训练误差和真实误差很接近

3. 好的算法 (good algorithm)：算法可以选出一个训练误差很小的假设

4. 好的运气 (good luck)：因为前三点说明的在概率上近似正确 (PAC)，所以需要一点运气使得坏事不会发生

 

在模型复杂度上，找一个最优 VC 维度最小化真实误差；在样本复杂度上，至少用“10 倍的 VC 维度”数量的训练数据。

下一贴讲支持向量机 (support vector machine, SVM)。Stay Tuned!

附录

1

NFL 定理

定义

    A 为算法

    xin 为样本内数据

    xout 为样本外数据 (N 个)

    c 为目标函数

    h 为假想函数

在考虑所有 c 的情况，算法 A 在样本外误差期望为

以上证明第四行是因为当 c 是均匀分布时，c 和 h 有一半的时候预测结果不一致，因为样本外有 N 个数据，那么 c 一共有 2N 预测结果，一半就是 2N-1。

上述结果显示总误差竟然和算法 A 无关，那么我们有

    E[胡猜算法|c] = E[高级算法|c]

也就是说胡猜算法和高级算法的期望误差或者期望性能相同。

2

霍夫丁不等式

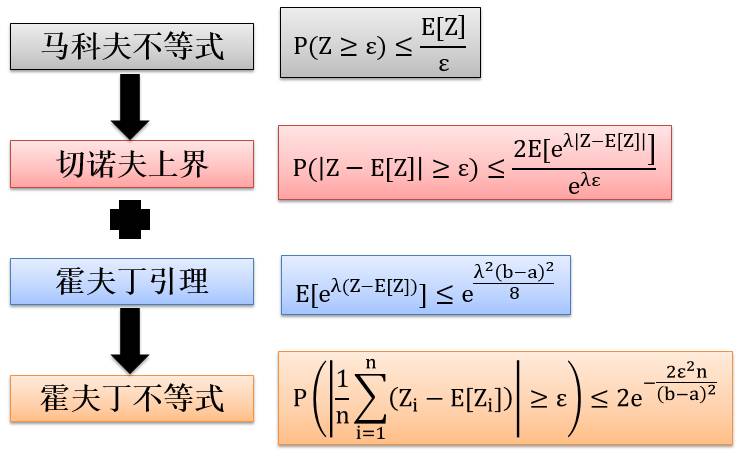
霍夫丁不等式 (Hoeffding’s Inequality) 是由切诺夫上界 (Chernoff Bound) 和霍夫丁引理 (Hoeffding’sLemma) 一起证明出来的，而切诺夫上界是由马科夫不等式 (Markov’s inequality) 证明出来的。它们之间相互关系如下图：

上面各种定理和其假设总结于下表，紧跟着它们的完整证明。

马科夫不等式

假设 Z ≥ 0, ε > 0

证明

• 第一行是概率和指示函数的等价变化

• 第二行是因为指示函数小于等于 1

• 第三行是因为 Z ≥ ε  

• 第四行是因为 ε 不是随机变量而 Z 是随机变量

切诺夫上界

假设 λ ≥ 0, ε > 0

证明

• 第一行是因为当 λ ≥ 0，exp(λx) 是增函数

• 第二行直接套用马可夫不等式

同理可证

将上面两个不等式综合成一个

霍夫丁引理

假设 λ ≥ 0

证明

• 第二行令 X = Z – E[Z], 假设 a ≤ X ≤ b

• 第三行 eX 是 X 的凸函数

• 第四行 E[X] = E[Z] – E[E[Z]] = 0

• 第五行做恒等变形

• 第六行令 h = λ(b-a) 和 p = -a/(b-a)

• 第七行令 L(h) = -hp + ln(1-p+peh)

• 第八行计算

• L’(h) = -p + peh/(1-p+peh)

• L”(h) =  (1-p)peh/(1-p+peh)2

因此 L(0) = L’(0) = 0, L”(0) ≤ 0.25，再用泰勒公式展开

• 第九行把 h 带入

霍夫丁不等式

假设 Zi 是 i.i.d, a ≤ Zi ≤ b, ε > 0

证明

• 第二行令 X = Σni=1 Zi

• 第三行直接套用切诺夫上界

• 第四行因为Zi i.i.d

• 第五行对 Zi 用霍夫丁引理

• 第六行整理表达式

• 第七行在 λ 上求最小值 (因为对任意 λ 都成立)

当 Zi 服从伯努利分布时，那么 a = 0 和 b = 1，将上式和机器学习挂钩得到

         

3

增长函数上界

定义 B(n,k) 是 n 个点上突破点为 k 时的最多对分个数，或者是 n 个点上任意 k 个点不能被打散的最多对分个数。

 

下图展示了 B(3,2) 和 B(4,2) 图，很容易可以看出在下图列出的对分情况下不能再加新的对分了，比如 B(3,2) 加“黑黑白” x1 和 x2 被打散了，加“黑白黑” x1 和 x3 被打散了，加“白黑黑” x2 和 x3 被打散了。

接下来看 B(4,3)，首先通过尝试找出最大对分个数是 11 使得任意 3 个点不被打散。

然后我们期望推出 B(4,3) 和 B(3,3) 之间的关系，做法如下：

1. 将 B(4,3) 对分排序，形单影只的对分定义为 α，成双成对的对分定义为 β，则 B(4,3) = α + 2β

2. α + β ≤ B(3,3) 因为 B(4,3) 都不能被 3 个点打散

3. β ≤ B(3,2) 因为如果 β 能被 2 个点打散，那么 2β 一定能被 3 个点打散 (x4 有空心有实心)，但其实没有

4. 因此 B(4,3) ≤ B(3,3) + B(3,2)

更一般的有

    B(n,k) ≤ B(n-1,k) + B(n-1,k-1)

 

现在用归纳法来证明

首先验证：当 n = 1, k = 1时，B(1,1) = 1 满足要证的不等式

假设在 n 时要证的不等式成立，那么在 n+1 时也成立，如下：

根据 B(n,k) 的定义是 n 个点上突破点为 k 时的最多对分个数，那么也是 B(n,k) 增长函数的上界，因此