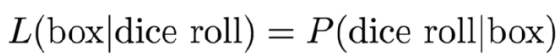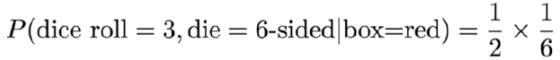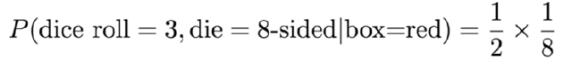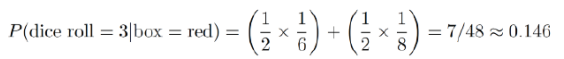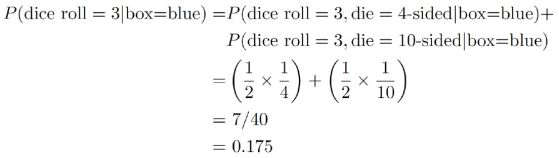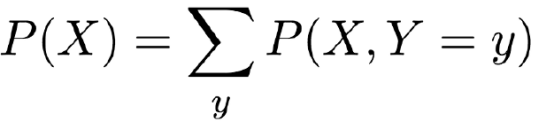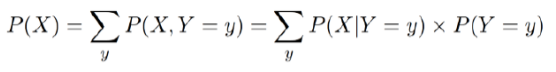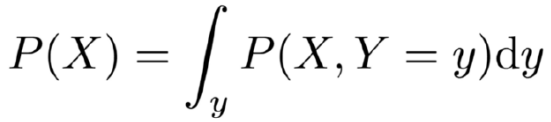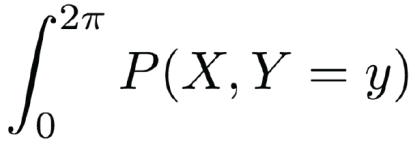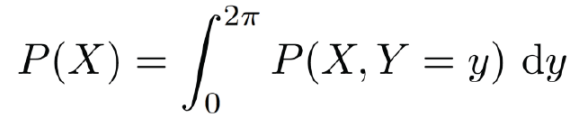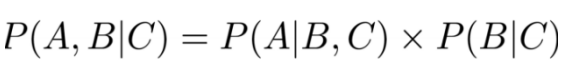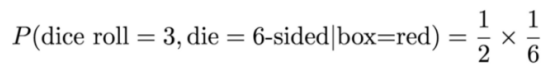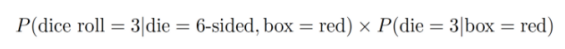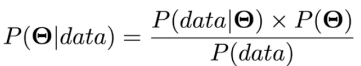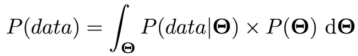概率论之概念解析：边缘化（Marginalisation）

2018 年 1 月 31 日 专知专知内容组（编）

【导读】前不久，专知内容组为大家整理了数据科学家Jonny Brooks-Bartlett的系列博客（包括概率论引言、极大似然估计、贝叶斯参数估计等），引起不错的反响，前两天Jonny Brooks-Bartlett又退出了最新的技术博客“概率论概念解释：边缘化（Marginalisation）”。继承其系列博客的优良传统，这篇文章依然保持通俗易懂、深入浅出的风格，内容主要围绕概率论的“边缘化的概念”进行呢详细的介绍，并通过一个例子来解决一个简单的“极大似然问题”。OK！话不多说，让我们一起学习今天的内容吧。专知内容组编辑整理。

概率论基础概念系列博客——概率论之概念解析：引言篇，极大似然估计，贝叶斯推断，阅读专知以前推出的报道：

概率论之概念解析：引言篇

概率论之概念解析：极大似然估计

概率论之概念解析：用贝叶斯推断进行参数估计

Probability concepts explained:Marginalisation

概率论概念解释：边缘化

▌引言（Introduction）

在这篇文章中，我将解释边缘化的概念，并通过一个例子来解决一个相当简单的[极大似然问题]。这篇文章涉及到的一些关于基本概率概念的知识，你可以在本系列的[介绍性博客文章]中找到。

链接：

https://towardsdatascience.com/probability-concepts-explained-maximum-likelihood-estimation-c7b4342fdbb1

https://towardsdatascience.com/probability-concepts-explained-introduction-a7c0316de465

▌什么是边缘化（What is marginalisation）

边缘化是一种方法，它要求对一个变量的可能值求和，以确定另一个变量的边缘贡献。这个定义可能听起来有点抽象，让我们用一个例子来说明这一点。

假设我们对天气如何影响英国人的幸福这一话题感兴趣。我们可以把它写成P(幸福|天气)，即给定天气类型的情况下一个人的幸福水平的概率是多少。

假设我们有测量一个人幸福所需的设备和定义，并记录了一个人所在的英格兰和另一个人所在的苏格兰的天气情况。现在，通常来说苏格兰人比英格兰人更幸福。问题是，人们总是有国籍的，所以在测量中我不能摆脱这个因素。所以我们实际测量的是P(幸福，国家|天气)，即我们同时关注幸福和国家。

边缘化告诉我们，如果我们把所有国家的可能性都加起来，我们可以计算出我们想要的数量(记住，英国是由三个部分组成的:英格兰、苏格兰和威尔士)，即P(幸福，国家=英格兰|天气)+ P(幸福，国家=苏格兰|天气)+ P(幸福，国家=威尔士|天气)。

而就是这样！边缘化告诉我们，只要把一些概率加起来就能得到所需的概率量。一旦我们计算出了答案(它可以是一个单个值或一个分布)，我们就可以得到我们想要的任何属性(推理)。

▌相关定义（Related definitions）

如果这个概念听起来你觉得熟悉，但你以前没有听说过边缘化，这可能是因为你听说的是它的另一个名字。有时这种方法被称为对妨害变量（nuisance variable）进行积分。积分本质上是对一个变量进行累加（“adding up”）的另一种说法，你正在求和的变量被称为“妨害变量”（“nuisance variable”）。所以在上面的例子中，“国家”这个变量是妨害变量。

如果你正在使用[概率图模型]，那么边缘化是你可以执行精确推断的一种方法（也就是说，你可以从你感兴趣的分布中记下确切的数量，例如可以从分布中精确计算均值）。在这种情况下，边缘化是[变量消除]的一种方法，有时被用作同义词来代替。

链接：

https://blog.statsbot.co/probabilistic-graphical-models-tutorial-and-solutions-e4f1d72af189

https://en.wikipedia.org/wiki/Variable_elimination

▌举例：骰子游戏

我将会讲一个例子，这是世界上最好的数学和计算晶体学家之一Airlie J. McCoy所写的论文中的例子。如果你正在寻找一个关于骰子的各种极大似然概念的很好的介绍(例如，对数似然，中心极限定理等)，那么我强烈推荐它。

假设我们有四个不同类型的骰子:4面骰子，6面骰子，8面骰子和10面骰子(如下图所示)。

图：我们有4个骰子。从左到右依次是:4面骰子，6面骰子，10面骰子和8面骰子。

关于游戏

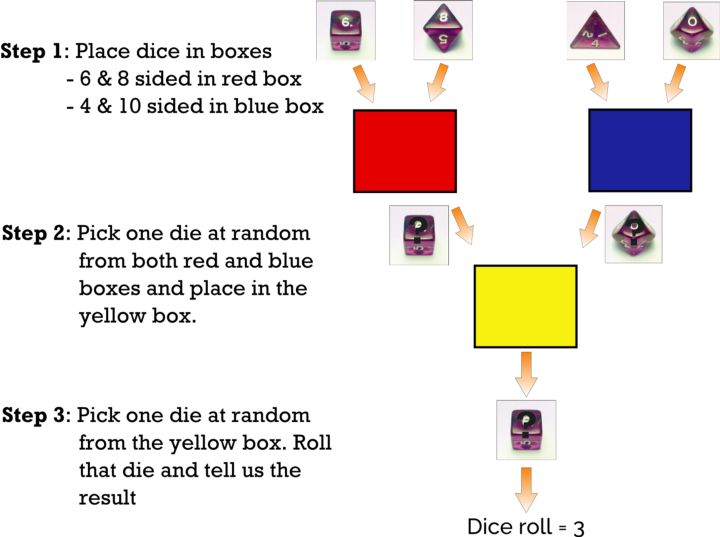
我把6面和8面的骰子放在一个红色的盒子里，4面和10面的骰子放在一个蓝色的盒子里。
我从每个红蓝盒子中随机选择一个骰子，然后把它们放在一个黄色的盒子里。
我从黄箱子里随机选择一个骰子，掷骰子并告诉你结果。

玩完游戏后，我们被告知结果是3。我们想要回答的问题是:骰子最可能是来自红盒子还是蓝盒子?*

图：关于游戏过程的图形描述

解决方案

为了解决这个问题，我们必须计算出骰子从红盒子中取出的可能性，因为我们掷出了一个3, 即L(box=red| dice roll =3)，以及我们掷了一个3，并且骰子从蓝色方框中被选中的可能性是L(box=blue| dice roll =3)。无论哪个概率是最高的，都是我们给出答案。（这里面dice roll是指掷骰的意思）

那么我们如何计算L(box=red| dice roll=3)和L(box=blue| dice roll=3)?

首先要知道的是，可能性和概率是通过如下等式联系起来的:

关于这个式子的详情请参阅我的博文：

https://towardsdatascience.com/probability-concepts-explained-maximum-likelihood-estimation-c7b4342fdbb1

这意味着可能性L(box=red| dice roll =3)，等同于骰子来自于红框，投掷出3的概率，即P(dice roll =3|box=red)。类似地，L(box=blue| dice roll =3) = P(dice roll =3| box=blue)。

假设我们选了一个红盒子里的骰子。它可以是六面骰子，也可以是八面骰子，每个骰子都是50/50的机会。假设我选择了六面骰子。这意味着我必须从黄色盒子中选择6面骰子然后掷出3。所以在这种情况下，概率由以下公式给出：

这个公式中，“1/2”是因为我有50％的几率从红色的盒子里随机挑选6面的骰子（因为盒子中还有8面的骰子，所以是1/2）。 “1/6”来自于这个6面骰子有六个面的事实，因此有1/6的机会投掷出3。

请注意，答案中没有包含从黄色盒子中选取六面骰子的概率。这是因为在这种情况下，从黄色盒子中拾取六面骰子的概率是1（你可能以为它是1/2，因为黄色盒子包含了6面骰子，同时也包含了从蓝色的盒子中取出来的骰子）。这是因为我们正在计算从红色盒子中取出一个六面骰子掷出一个3的条件概率，因此，黄色箱子里的另一种情况是不可能的，因为另一种情况原本是从蓝箱子里拿来的。所以前提条件是从红色箱子取出，六面骰子只在红色的箱子里，所以我们从黄色箱子中选择六面骰子的概率是1。

用同样的方法我们可以计算取出一个八面骰子（实际上从红色盒子中取出），投掷出3的概率是：

现在我们已经做了几乎所有的工作来计算骰子来自红色盒子的可能性。请记住，红色盒子中只包含了6面和8面的骰子，所以我们需要做的是找到这个骰子是6面或8面的概率。从第一段介绍性的文字中，我们知道在“或”情况下，我们需要把概率相加。所以骰子来自红色盒子的概率是：

上面等式中“波浪”等号的意思是“近似等于”。它的真正的答案是0.1458333333 ......（这3个是永远继续下去的，我们说它是3的循环），但是我很懒，只给了小数点后三位数字的回答（即四舍五入到小数点后三位）。要明确的是，我们没有给出精确的答案，我们通常使用“波浪”等号。

接下来，我们可以对蓝色盒子进行相同的计算，得到：

骰子最初来自蓝色盒子的可能性更高，因此使用极大可能性我们可以得出结论，骰子最有可能来自蓝色盒子。

这个例子中的边缘化在哪里？

对于那些非常善于观察的人，你会注意到，在这个例子中，我没有使用过“边缘化”这个词。这是因为我想让你们直观理解如何计算从盒子中取出骰子的概率。

如果你看一下上面这个计算蓝色盒子的方程，你会看到我们把所有可能性的概率加在一起，即选择4面骰子和10面骰子。这就是边缘化！我们相加了这个讨厌的变量（骰子）。注意在那个游戏中，我们从来没有观察到我们选择的骰子，因为我们不需要！我们需要知道的是结果（掷骰子= 3）和所有可能的骰子值。这就是为什么它如此强大。我们可以计算我们从未观察过的事物的概率。只要我们知道可能的妨害变量值，我们就可以用它来执行边缘化，并计算不同变量的分布。

关于符号

下面是让我们写一些更可怕的方程式的部分，但请大家宽容我，我会尽我所能使其容易理解。

让我们来思考我们刚才在这个例子中做了什么。我们以一个联合概率开始，P（掷骰子，骰子|盒子）（即掷骰子是3，骰子是我们选择的骰子，而盒子是最初的盒子;蓝色或红色）。一旦我们进行边缘化，我们能够得到一个条件概率，P（掷骰子|盒子）。这是边缘化的主要好处之一。我们可以从联合概率转变成条件概率。

实际上，我们也可以从联合概率到边缘概率。如果你看到边缘化的数学定义，这通常是你会看到的形式。如果你还没有看到数学的定义，...。你很幸运。你即将看到它。

这个大写的"Σ"把所有一切相加的偷懒写法，它下面的“y”告诉我们应该把什么相加起来。所以这个等式意思是说“如果你想要得到X(等式左边)的边缘概率，那么你需要对变量Y的每一个可能的结果来计算X和Y的联合概率值。”

联合概率有时候是很难处理的，所以我们可以用[一般乘法法则](https://www.khanacademy.org/math/ap-statistics/probability-ap/probability-multiplication-rule/a/general-multiplication-rule)重写右侧的联合概率。

方程的右边写成条件分布和边缘分布的乘积的形式，有时更容易计算。

像我之前提到的，Σ的意思是把所有的东西相加。我没有提到的是，只有当变量是“离散的”时候才使用特定的符号。我的意思是变量只能取有限的数值。在前面的例子中，我们相加了离散的妨害变量（例如，英国的国家只能是英格兰，威尔士或苏格兰，而骰子只有有限的结果，例如1到6）。离散值不一定是有限的。例如，它们可以是所有的正整数（即正整数），如1,2,3，...。等等

然而，当我们使用在给定边界内具有无限可能值的变量时（例如0到10米之间的距离度量可以具有无限数量的值，例如5米，5.1米，5.01米，5.001米，5.0001 m，...等等），我们把这些称为“连续变量”，我们不使用“Σ”符号。相反，我们使用“ ∫ ”。这个符号仍然告诉我们，我们必须把所有东西都加起来，但是我们知道，这时候妨害变量是连续的，所以把边缘化写成：

这意味着与上述离散变量情况下的边缘化方程相同。最后的“dy”告诉我们要把什么求积分（“积分”是我们用在连续变量的表示“加起来”的意思）。

“dy”是必要的原因是，如果我们不声明它，它并不总是很明显。考虑一下这个情况，其中妨害变量是一个圆周的角度。我们知道角度在0到360度之间，或者从技术上讲，我们喜欢用弧度而不是度，我们说角度从0到2π

来源：维基百科。一个圆周中的弧度

所以我们可能会写成如下的形式：

我们知道，我们需要对0到2π之间的值求积分，但是我们是对X的值求呢还是对Y的值求呢？提出这个问题，世界各地的数学家都恨不得把我的脸狠狠地揍一顿。

为了解决这个问题，我们把“dy”放在最后，清楚地表明我们将对0和2π之间的Y值进行积分，这意味着我们也知道结构是求X的边缘分布（下面所示）。

对于感兴趣的人来说，从0到2π求积分是我们在X射线晶体学领域（我的博士领域）所要做的事情，因为这个问题叫做[相位问题](https://en.wikipedia.org/wiki/Phase_problem)。这基本上是我们无法测量实验中“相位”的问题，而相位可以像一个角度一样被数学化处理。因此，为了计算我们观察到的数据的理论分布，我们不得不边缘化这些相位。

亚当·凯勒（[Adam Kelleher](https://medium.com/@akelleh)）利用因果关系中的边缘化来消除混杂因素的影响（https://github.com/akelleh/causality ）。他还使用一般的乘法规则，如上所述，用条件分布和边缘分布的乘积来写出边缘化。你可以在他的[博客文章](https://medium.com/@akelleh/causal-inference-with-pandas-dataframes-fc3e64fce5d)中阅读。

▌结束语