斯坦福/谷歌大脑：两次蒸馏，引导扩散模型采样提速256倍！

---

  新智元报道  

编辑：Aeneas David

【新智元导读】斯坦福、谷歌大脑新作：无需分类器，两步蒸馏，将扩散模型采样速度提升256倍。

最近，无分类器的指导扩散模型(classifier-free guided diffusion models)在高分辨率图像生成方面非常有效，并且已经被广泛用于大规模扩散框架，包括DALL-E 2、GLIDE和Imagen。

然而，无分类器指导扩散模型的一个缺点是它们在推理时的计算成本很高。因为它们需要评估两个扩散模型——一个类别条件模型(class-conditional model) 和一个无条件模型(unconditional model)，而且需要评估数百次。

为了解决这个问题，斯坦福大学和谷歌大脑的学者提出使用两步蒸馏(two-step distillation)的方法来提升无分类器指导扩散模型的采样效率。

论文地址：https://arxiv.org/abs/2210.03142

如何将无分类器指导扩散模型提炼成快速采样的模型？

首先，对于一个预先训练好的无分类器指导模型，研究者首先学习了一个单一的模型，来匹配条件模型和无条件模型的组合输出。

随后，研究者逐步将这个模型蒸馏成一个采样步骤更少的扩散模型。

可以看到，在ImageNet 64x64和CIFAR-10上，这种方法能够在视觉上生成与原始模型相当的图像。

只需4个采样步骤，就能获得与原始模型相当的FID/IS分数，而采样速度却高达256倍。

可以看到，通过改变指导权重w，研究者蒸馏的模型能够在样本多样性和质量之间进行权衡。而且只用一个取样步骤，就能获得视觉上愉悦的结果。

扩散模型的背景

通过来自数据分布 的样本x，噪声调度函数 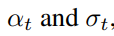研究者通过最小化加权均方差来训练了具有参数θ的扩散模型 。

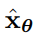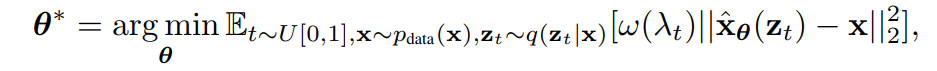
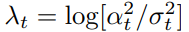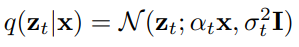其中 是信噪比， 和 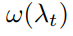是预先指定的加权函数。

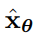一旦训练了扩散模型 ，就可以使用离散时间DDIM采样器从模型中采样。

具体来说，DDIM采样器从 z1 ∼ N (0,I)开始，更新如下

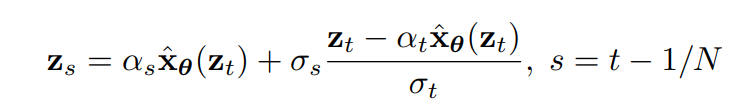
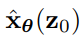其中，N是采样步骤的总数。使用 ，会生成最终样本。

无分类器指导是一种有效的方法，可以显著提高条件扩散模型的样本质量，已经广泛应用于包括GLIDE，DALL·E 2和Imagen。

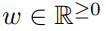它引入了一个指导权重参数 来衡量样本的质量和多样性。为了生成样本，无分类器指导在每个更新步骤都会使用 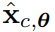作为预测模型，来评估条件扩散模型 和联合训练的 。

由于每次采样更新都需要评估两个扩散模型，因此使用无分类器指导进行采样通常很昂贵。

为了解决这个问题，研究者使用了渐进式蒸馏(progressive distillation)  ，这是一种通过重复蒸馏提高扩散模型采样速度的方法。

在以前，这种方法不能直接被直接用在引导模型的蒸馏上，也不能在确定性DDIM采样器以外的采样器上使用。而在这篇论文中，研究者解决了这些问题。

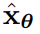蒸馏无分类器的指导扩散模型

他们的办法是，将无分类器的指导扩散模型进行蒸馏。

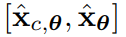对于一个训练有素的教师引导模型 ，他们采取了两个步骤。

第一步，研究者引入了一个连续时间的学生模型，它具有可学习的参数η1，来匹配教师模型在任意时间步长t ∈ [0, 1] 的输出。指定一系列他们有兴趣的指导强度后，他们使用以下目标来优化学生模型。

其中 。

为了结合指导权重w，研究者引入了w条件模型，其中w作为学生模型的输入。为了更好地捕捉特征，他们将傅里叶嵌入应用w，然后用Kingma等人使用的时间步长的方式，把它合并到扩散模型的主干中。

由于初始化在性能中起着关键作用，研究者初始化学生模型时，使用的是与教师条件模型相同的参数（除了新引入的与w-conditioning相关的参数）。

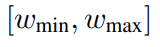
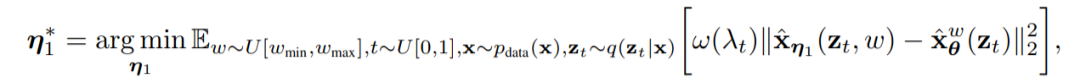
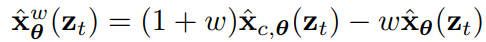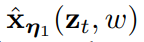第二步 ，研究者设想了一个离散的时间步长场景，并且通过每次将采样步数减半，逐步将学习模型从第⼀步 蒸馏成具有可学习参数η2、步⻓更少的学⽣模型 。

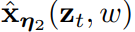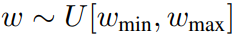其中，N表⽰采样步骤的数量，对于 和 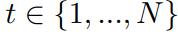，研究者开始训练学生模型，让它用一步来匹配教师模型的两步DDIM采样的输出（例如：从t/N到t - 0.5/N，从t - 0.5/N到t - 1/N）。

将教师模型中的2N个步骤蒸馏成学生模型中的N个步骤以后，我们可以将新的N-step学生模型作为新的教师模型，然后重复同样的过程，将教师模型蒸馏成N/2-step的学生模型。在每⼀步，研究者都会⽤教师模型的参数来初始化学⽣模型。

N-step的确定性和随机采样

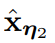⼀旦模型 被训练出来，对于 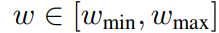，研究者就可以通过DDIM更新规则来执行采样。研究者注意到，对于蒸馏模型 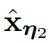，这个采样过程在给定初始化 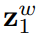的情况下是确定的。

另外，研究者也可以进行N步的随机采样。使用两倍于原始步长的确定性采样步骤（ 即与N/2-step确定性采样器相同），然后使用原始步长进行一次随机步回（即用噪声扰动）。

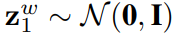，当t > 1/N时，可用以下的更新规则——

其中， 。

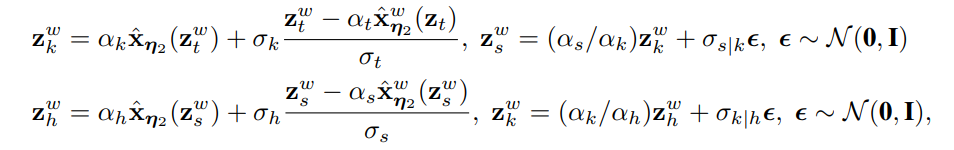
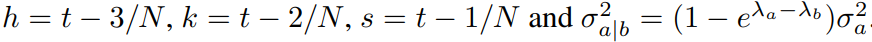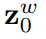当t=1/N时，研究者使用确定性更新公式，从 得出 。

值得注意的是，我们注意到，与确定性的采样器相比，执行随机采样需要在稍微不同的时间步长内评估模型，并且需要对边缘情况的训练算法进行小的修改。

其他蒸馏⽅法

还有一个直接将渐进式蒸馏应⽤于引导模型的方法，即遵循教师模型的结构，直接将学⽣模型蒸馏成⼀个联合训练的条件和⽆条件模型。研究者尝试了之后，发现此⽅法效果不佳。

实验和结论

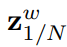模型实验在两个标准数据集上进行：ImageNet（64*64）和 CIFAR 10。

实验中探索了指导权重w的不同范围，并观察到所有的范围都有可比性，因此使用[wmin, wmax] = [0, 4]进行实验。使用信噪比损失训练第一步和第二步模型。

基线标准包括DDPM ancestral采样和DDIM采样。

为了更好地理解如何纳入指导权重w，使用一个固定的w值训练的模型作为参照。

为了进行公平比较，实验对所有的方法使用相同的预训练教师模型。使用U-Net（Ronneberger等人，2015）架构作为基线，并使用相同的U-Net主干，引入嵌入了w的结构作为两步学生模型。

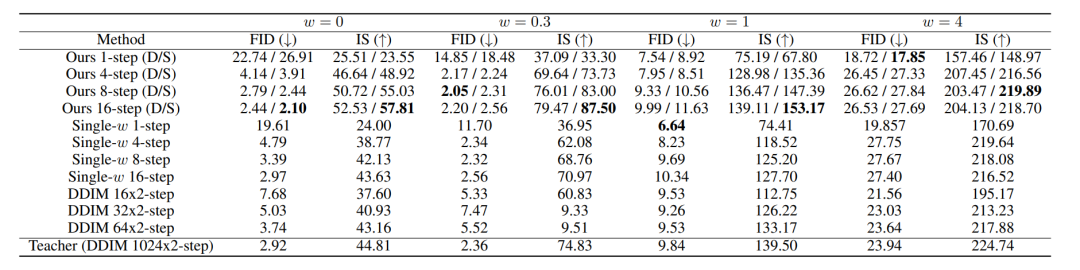
上图为所有方法在ImageNet 64x64上的表现。其中D和S分别代表确定性和随机性采样器。

在实验中，以指导区间w∈[0, 4]为条件的模型训练，与w为固定值的模型训练表现相当。在步骤较少时，我们的方法明显优于DDIM基线性能，在8到16个步骤下基本达到教师模型的性能水平。

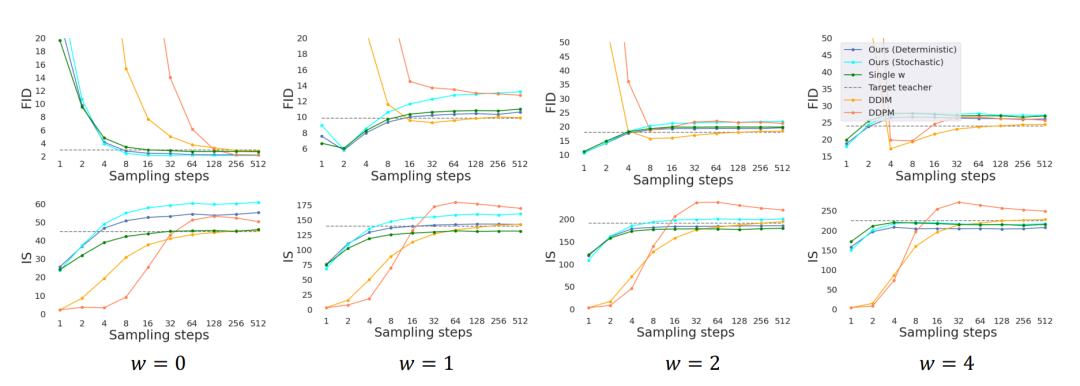
由FID和IS分数评估的ImageNet 64x64采样质量

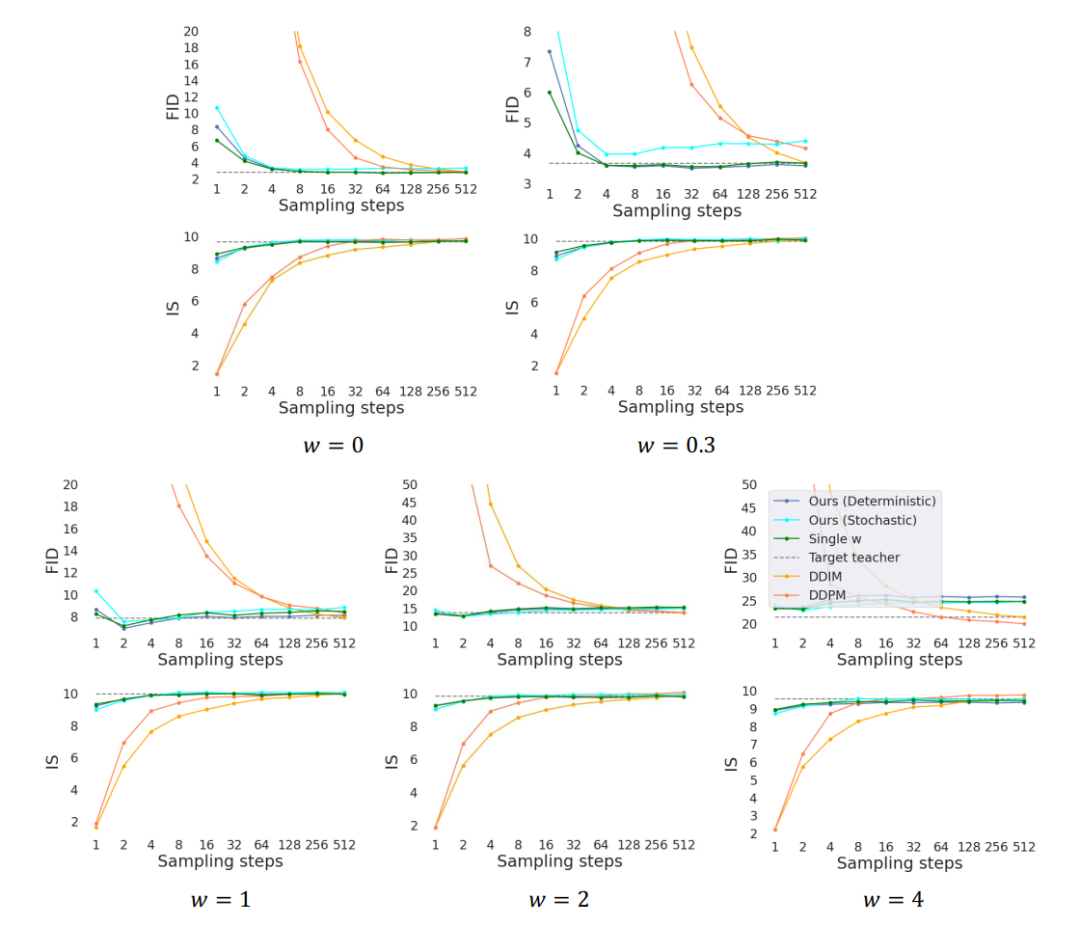
由FID和IS评分评估的CIFAR-10采样质量

我们还对教师模型的编码过程进行蒸馏，并进行了风格转移的实验。具体来说，为了在两个领域A和B之间进行风格转换，用在领域A上训练的扩散模型对领域A的图像进行编码，然后用在领域B上训练的扩散模型进行解码。

由于编码过程可以理解为颠倒了的DDIM的采样过程，我们对具有无分类器指导的编码器和解码器都进行了蒸馏，并与DDIM编码器和解码器进行比较，如上图所示。我们还探讨了对引导强度w的改动对性能的影响。

总之，我们提出的引导扩散模型的蒸馏方法，以及一种随机采样器，从蒸馏后的模型中采样。从经验上看，我们的方法只用了一个步骤就能实现视觉上的高体验采样，只用8到16个步骤就能获得与教师相当的FID/IS分数。

参考资料：

https://twitter.com/chenlin_meng/status/1579384412068016128

https://www.reddit.com/r/MachineLearning/comments/y0iu5w/new_distilled_diffusion_models_research_can/

https://arxiv.org/abs/2210.03142