【机器学习】朴素贝叶斯

2019 年 12 月 11 日 深度学习自然语言处理

点击上方，选择星标或置顶，每天给你送干货！

阅读大概需要10分钟

跟随小博主，每天进步一丢丢

转载自：AI小白入门

本文介绍了朴素贝叶斯模型，朴素贝叶斯（几乎所有的概率模型）的核心假设：特征之间的条件概率相互独立。以垃圾邮件分类问题为例，分析了朴素贝叶斯模型的两种应用场景：1）先验分布和条件概率分布都为一元伯努利分布，2）先验分布为一元伯努利分布，条件概率分布为多元伯努利分布。分别对应词袋子表示中两种常用的方法: one-hot表示，编号表示（词频表示）。

作者 | 文杰

编辑 | yuquanle

朴素贝叶斯

A、朴素贝叶斯

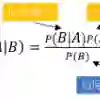
朴素贝叶斯模型也是一个典型的生成模型，一般用来处理离散值数据（伯努利分布导致）。其核心假设是特征之间的条件概率是相互独立的。同样由贝叶斯公式有：

下面以垃圾邮件分类介绍两类问题的朴素贝叶斯模型：

垃圾邮件分类任务是一个基本文本分类任务，涉及到NLP的初步知识-文本的One-hot表示。由于机器学习模型通常是一个数学模型，而非数值型属性是不能直接处理，所以一般对邮件的特征进行编码。首先将所有的邮件中出现的词统计出来作为一个词典，并对每一个词进行编码向量化（即词序）。一封邮件对应的One-hot表示如下：

其中表示第封邮件，，表示词典中的第个词，如果第个词在第封邮件中出现则，反之为。可以看出这种表示忽略了文本的大量信息，上下文信息，词出现的次数等。

由上面的公式有，一封邮件是垃圾邮件的概率可以表示为下式：

其中似然函数为在垃圾邮件下产生的条件概率，为垃圾邮件的先验概率，对于所有样本都是一致，近似忽略。

由朴素贝叶斯的条件概率独立性假设有条件概率如下：

其中表示第个特征。所以，对于一封邮件属于哪一类的概率为都有：

邮件之间独立，所以目标函数最大化所有邮件属于各自类的概率为：

从上式可以看出朴素贝叶斯的参数是，即所有邮件类别的先验，以及在某一类下出现某个词的概率。由极大似然估计参数值即为其期望。

其中表示类别，对应垃圾邮件分类取值为表示第个特征，表示特征的取值。由于垃圾邮件中采用one-hot编码，所以的取值为，表示出现。当以上参数确定之后，对于一封新的邮件，根据估计的参数和贝叶斯公式求得样本属于哪一类的概率。最后一封邮件属于哪一类的概率参数表示如下：

one-hot编码比较特殊：

由于所有类的概率加和为，垃圾邮件为二分类，所以邮件属于概率大于的那一类。

为了使模型更具普适性，考虑到当某一特征没有在训练集中出现过，即某一个单词在某一类下没有出现过，或者某一单词在某一类下都出现过（意味着不出现的条件概率为0）。但不能说该单词在这一类下的条件概率为0。又或者在所有类中都未出现（即原始训练集中没有的词，而词典中有的词，即词典不依赖于训练集)。当来一个新样本时，如果不做处理，那么只要有一个分量的概率为0，由于特征之间的条件概率独立，连乘形式只要有一个为0，即整个概率为0，无意义。

拉普拉斯平滑：

其中为第个特征分量的可能取值数。

B、N元多项分布模型

同样，上述贝叶斯模型中只考虑单词是否出现，即单词特征服从伯努利分布，样本服从n次独立的伯努利分布。而忽略了一个单词可能出现次数对邮件分类的影响。假设要统计某一单词出现的次数，那么有多项分布。只考虑单词是否出现的贝叶斯模型叫multi-variate Bernoulli event model，后者叫multinational event model。

同样以邮件分类问题介绍multinational event model，在之前的模型中，我们首先建立词典，并且特征向量长度为词典长度，并且从词典出发，对于邮件出现过的单词，在对应词典的位置标记为，反之标记为产生一个特征向量。而multinational event model则从邮件出发，表示邮件中第个单词，其值表示第个单词在字典中出现的位置，那么的取值则有，其中V表示字典长度。这样一封邮件可以表示为，表示第封邮件的长度。这相当于掷一枚有V面的骰子次，将观测值记录下来形成一封邮件。假设出现某一点的情况与第几次掷无关，也就是单词在邮件中出现的位置无关，而且每一次投掷都是独立的，即单词之间出现的事件是独立的。

文档的表示：

one-hot表示

编号表示

可以看出两者方式的样本表示不同之处在于一个以词典维度对邮件中的词是否出现进行编码，一个是以邮件维度对邮件中的词在词典中的编号进行编码，这就导致了两者表示的维度不同，特征服从的分布也不同。

一封邮件属于垃圾邮件的概率由贝叶斯公式有：

其中似然函数，在垃圾邮件下产生的条件概率，为垃圾邮件的先验概率，对于所有样本都是一致，近似忽略。

由朴素贝叶斯的条件概率独立性假设有条件概率如下：

其中。同样最大化似然函数：

其中表示第封邮件的长度。所以上式中的参数有，。由最大似然估计有：

其中与无关，我们需要求的是所有可能的取值。

最后一封邮件属于哪一类的概率参数表示如下：

其中表示邮件第个词在词典中的编号。

one-hot表示和编号表示：

两种表示最大的差别在于包含的语义信息，one-hot表示信息不够丰富，只有，所以需要高的维度，而编号表示信息相对丰富，维度低。然而on-hot表示是可以直接度量两个样本之间的相似性的（表示是否存在，有语义意义的），而编号表示则不能直接度量两个样本之间的相似性（在词典中的编号是无语义的），但是可以把编号表示放回到集合中去度量两个样本的重合度。所以编号表示可以看作是one-hot的一种低维表示。

代码实战

int trainNB(Matrix X,Matrix Y)//训练函数的实现，注意对参数进行平滑处理
 {
 //类，特征，特征取值
 bayes.pY.initMatrix(CLASS_SUM,1,0,"ss");//两类初始化为2行的列向量
 bayes.pX_1Y.initMatrix(CLASS_SUM,X.col,0,"ss");//X_1Y表示在Y下X=1的概率，反之X=0的概率为1-
 bayes.pX.initMatrix(X.col,1,0,"ss");//
   int i,j,k;
 for(k=0; k<bayes.pX_1Y.row; k++)
 {
 for(i=0; i<bayes.pX_1Y.col; i++)
 {
 bayes.pX_1Y.data[k][i]=1;//平滑处理,默认出现一次，后期归一化时把特征向量的长度也考虑进去,这里的平滑是指每一类字典与整个字典的，未涉及测试
 //样本中的未登入词
 }
 }
 for(i=0; i<X.row; i++)
 {
 if(Y.data[i][0]==0)
 {
 bayes.pY.data[0][0]++;
 for(j=0; j<X.col; j++)
 {
 bayes.pX_1Y.data[0][j]+=X.data[i][j];
 }
 }
 else 
 {
 bayes.pY.data[1][0]++;
 for(j=0; j<X.col; j++)
 {
 bayes.pX_1Y.data[1][j]+=X.data[i][j];
 }
 }
 }
 for(i=0; i<X.col; i++)
 {
 //所有类下x各个特征分量出现的概率
 //bayes.pX.data[i][0]=(bayes.pX_1Y.data[0][i]-1) + (bayes.pX_1Y.data[1][i]-1) + 1;
 //bayes.pX.data[i][0]/=bayes.pY.data[0][0] + bayes.pY.data[1][0] + 2;
   //某一类下x各个特征分量出现的概率
 bayes.pX_1Y.data[0][i]/=bayes.pY.data[0][0] + 2;
 bayes.pX_1Y.data[1][i]/=bayes.pY.data[1][0] + 2;
   bayes.pX.data[i][0] = (bayes.pX_1Y.data[0][i] + bayes.pX_1Y.data[1][i])/2;
 }
 //计算出PY两类的概率
 for(k=0; k<bayes.pY.row; k++)
 {
 bayes.pY.data[k][0]/=X.row;
 }
 cout<<"pY="<<bayes.pY.data[0][0]<<endl;
   for(k=0; k<bayes.pX_1Y.row; k++)
 {
 for(i=0; i<bayes.pX_1Y.col; i++)
 {
 cout<<bayes.pX_1Y.data[k][i]<<" & ";
 }
 cout<<"---";
 }
 }