ICLR 2020 | Deformable Kernels,创意满满的可变形卷积核
论文提出可变形卷积核(DK)来自适应有效感受域,每次进行卷积操作时都从原卷积中采样出新卷积,是一种新颖的可变形卷积的形式,从实验来看,是之前方法的一种有力的补充。
作者 | VincentLee
编辑 | 贾 伟

论文地址:https://arxiv.org/abs/1910.02940
本文首发于公众号:晓飞的算法工程笔记

1、深入研究卷积

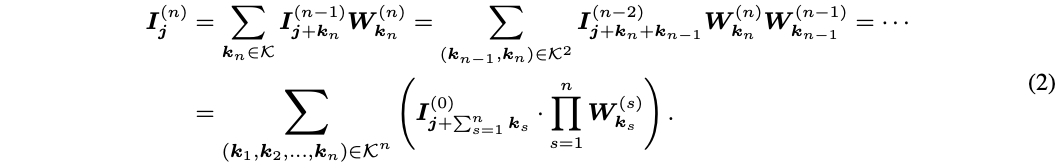
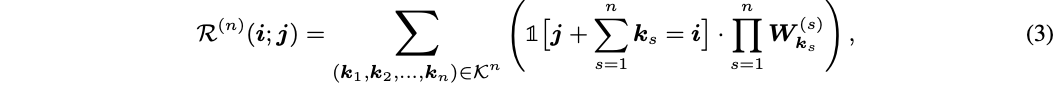
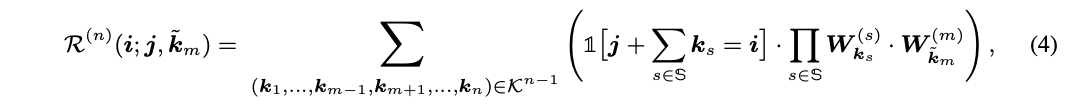
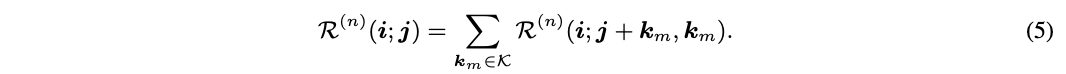
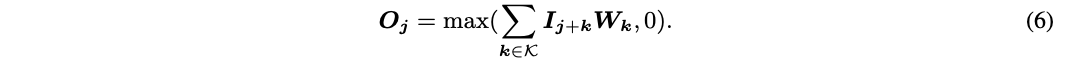
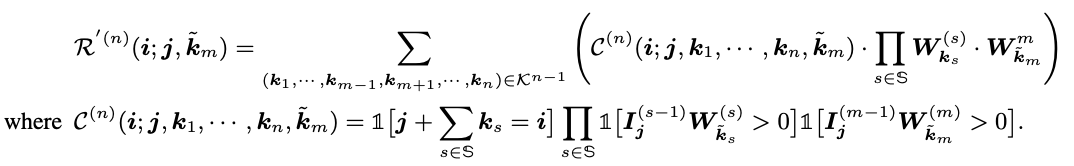
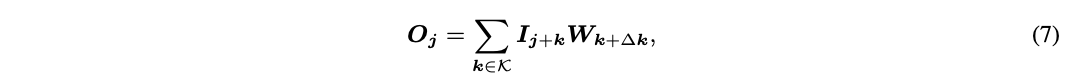
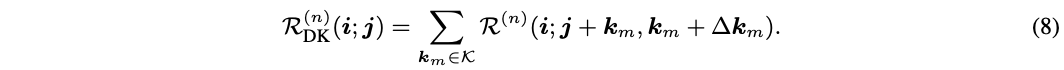
-
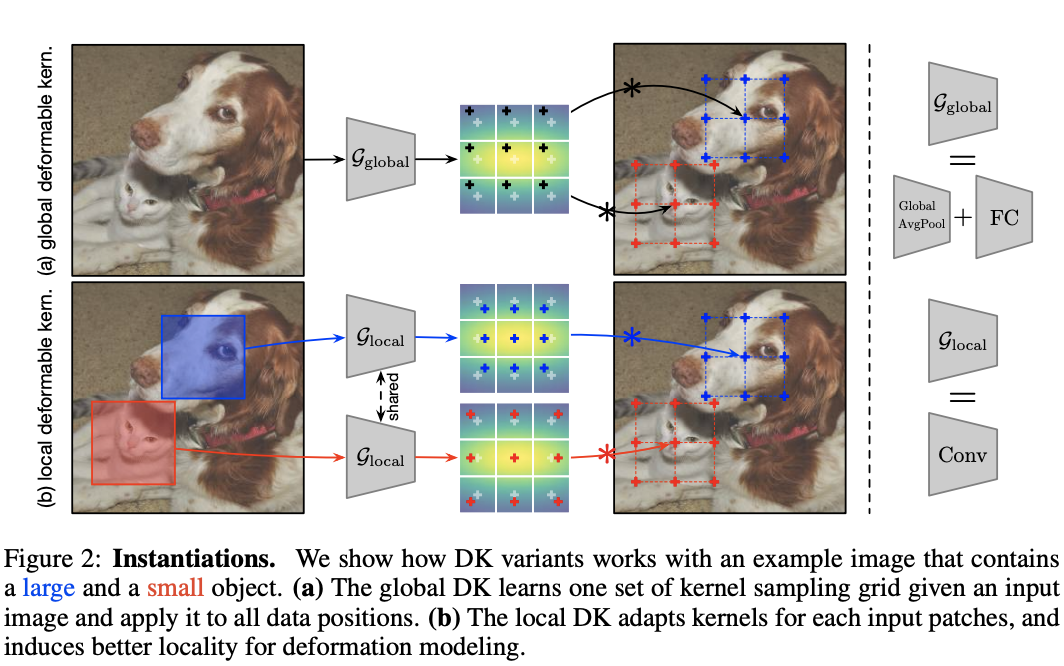
全局模式 的实现为global average pooling层+全连接层,分别用于降维以及输出 个偏移值。 -
局部模式 的实现为与目标卷积大小一样的卷积操作,输出为 维,最终输出为 。
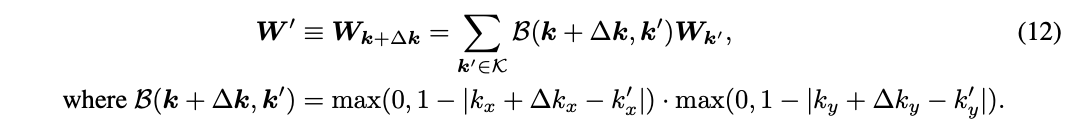
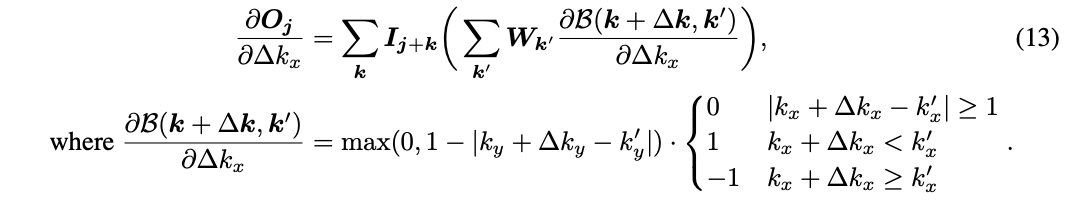
-
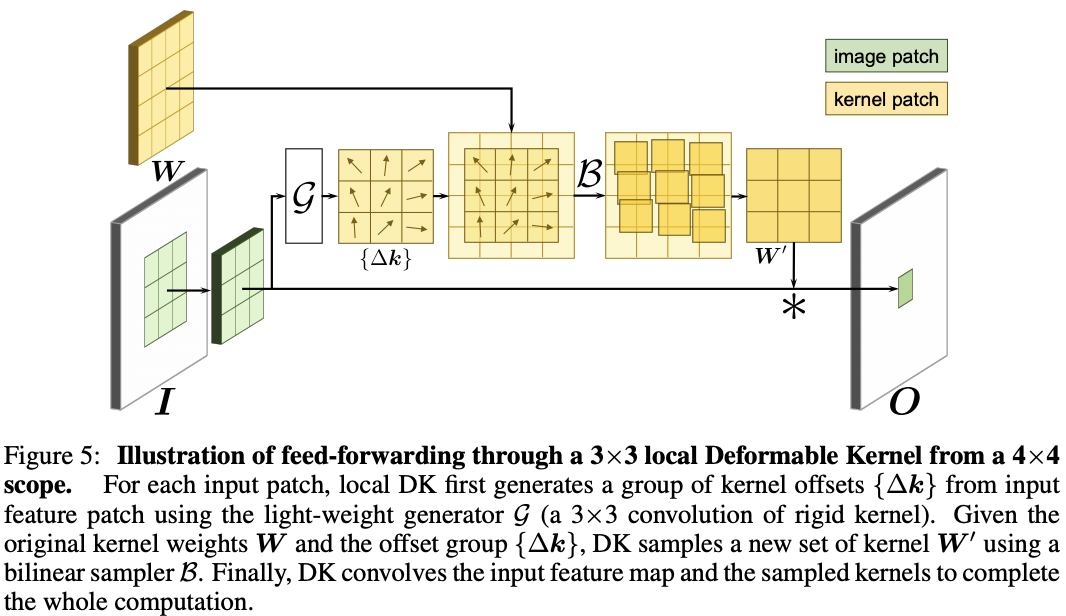
前一层特征图的梯度 -
当前层原生卷积的梯度 -
当前层偏移值生成器的梯度
5、可变形卷积连接
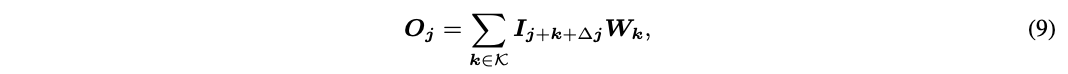
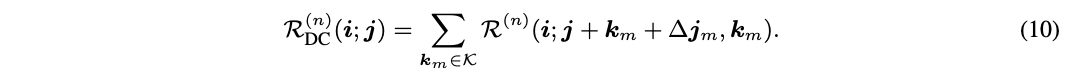
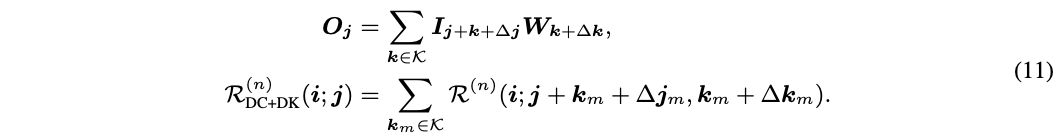

1、图像分类
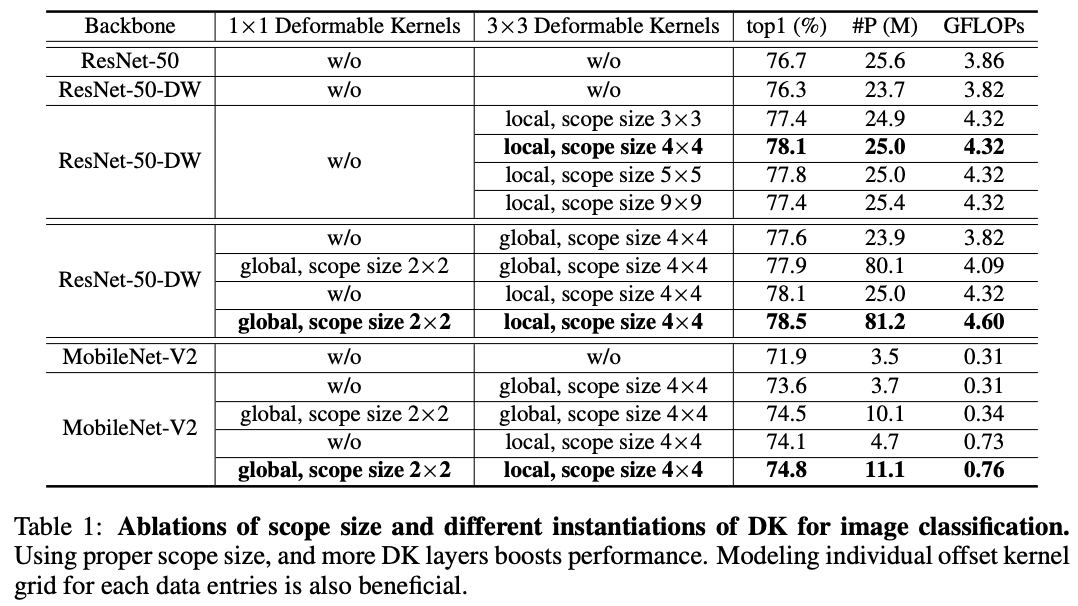
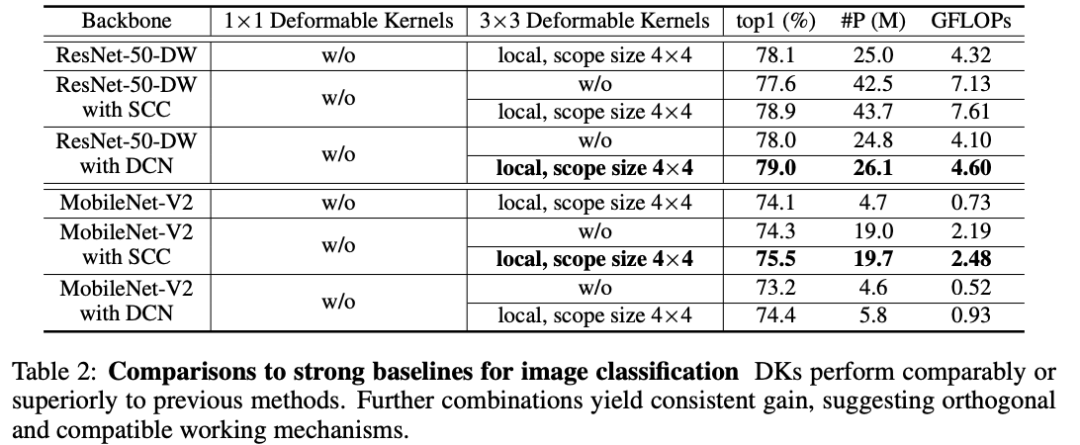
2、目标检测
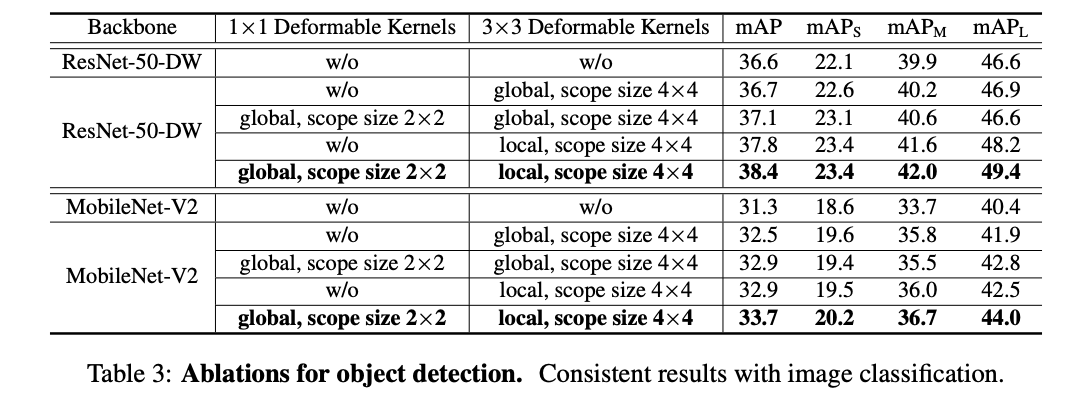

3、可变形核学习什么?


结 论
ICLR 2020 系列论文解读
疫情严重,ICLR2020 将举办虚拟会议,非洲首次 AI 国际顶会就此泡汤
疫情影响,ICLR 突然改为线上模式,2020年将成为顶会变革之年吗?
火爆的图机器学习,ICLR 2020上有哪些研究趋势?
1、直播
回放 | 华为诺亚方舟ICLR满分论文:基于强化学习的因果发现
03. Spotlight | 组合泛化能力太差?用深度学习融合组合求解器试试
04. Spotlight | 加速NAS,仅用0.1秒完成搜索
05. Spotlight | 华盛顿大学:图像分类中对可实现攻击的防御(视频解读)
06. Spotlight | 超越传统,基于图神经网络的归纳矩阵补全
07. Spotlight | 受启诺奖研究,利用格网细胞学习多尺度表达(视频解读)
08. Spotlight | 神经正切,5行代码打造无限宽的神经网络模型
4、Poster
01. Poster | 华为诺亚:巧妙思想,NAS与「对抗」结合,速率提高11倍
 点击“
阅读原文” 查看 CVPR 系列论文解读
点击“
阅读原文” 查看 CVPR 系列论文解读
登录查看更多
相关内容
Arxiv
8+阅读 · 2019年11月4日




