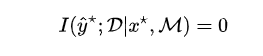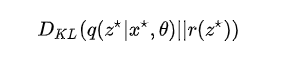ICLR 2020 | 告别死记硬背,元学习才能学会学习

论文: https://openreview.net/pdf?id=BklEFpEYwS
代码: https://github.com/google-research/google-research/tree/master/meta_learning_without_memorization
让我们回顾片刻在学校学习的经历。每一天我们去上课,回答老师的问题;回家后我们解答作业问题,对照答案检查正确与否。日积月累,我们不仅学到了知识,更学会了如何学习 (learning to learn)。当面对新任务时,我们可以利用之前解决问题的经验并加上少量的练习,迅速学会新的技能。这种 “快速适应 (fast adaptation)” 能力被认为是智能的重要体现。在人工智能领域,元学习 (meta-learning) 是一种使机器 “学会学习” 的有效手段。
在这篇论文里,我们发现一个表征能力强大的人工神经网络除了 “快速适应” 外,还可以通过 “记忆” 的方式来解决训练集里的多项任务。不幸的是,一个只会记忆的神经网络不具备解决新任务的能力。这篇论文旨在提出、定义、分析元学习中的记忆问题,并提出新的元正则化方法 (meta-regularization) 以避免记忆问题。
 中生成多个任务。每个任务都由一个带标注的任务内训练数据
中生成多个任务。每个任务都由一个带标注的任务内训练数据
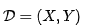 和测试数据
和测试数据
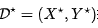 组成。我们用
组成。我们用
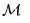 代表所有用于元训练(meta-training)的数据,
代表所有用于元训练(meta-training)的数据,
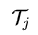 代表一个元测试阶段的新任务。
代表一个元测试阶段的新任务。
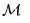 上训练模型, 目标是当面对新任务时,它能够在少量训练数据
上训练模型, 目标是当面对新任务时,它能够在少量训练数据
 上实现快速适应,从而准确预测新任务测试数据
上实现快速适应,从而准确预测新任务测试数据
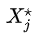 的标签。这个过程可以表示为一个层次型的图模型:
的标签。这个过程可以表示为一个层次型的图模型:
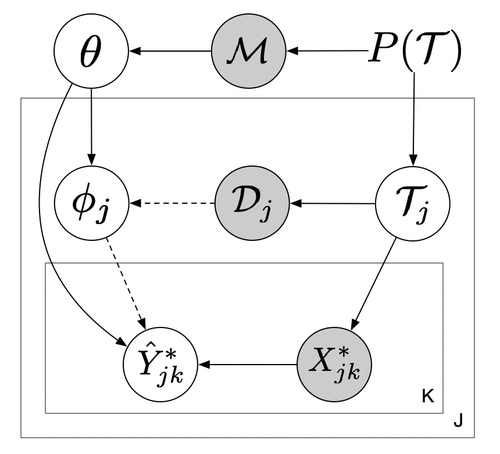
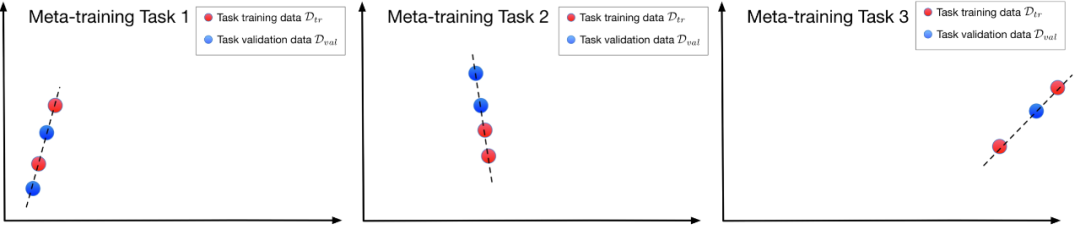
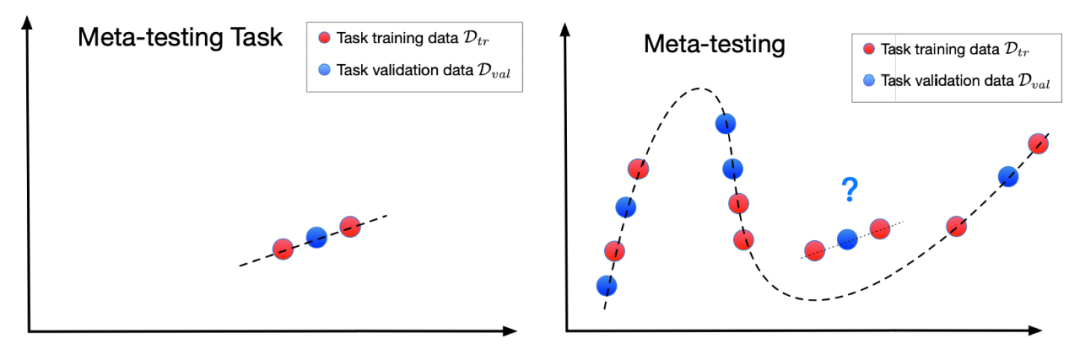
 紧密相关。我们发现,如果各任务是互斥的(mutually exclusive),意即一个单一预测模型不可以解决所有的任务,那么记忆问题不会出现。例如小样本分类(few-shot classification)广泛地利用了这个特性。但在很大一类问题中,各任务不互斥,因此记忆问题广泛存在,并会影响多种元学习算法。
紧密相关。我们发现,如果各任务是互斥的(mutually exclusive),意即一个单一预测模型不可以解决所有的任务,那么记忆问题不会出现。例如小样本分类(few-shot classification)广泛地利用了这个特性。但在很大一类问题中,各任务不互斥,因此记忆问题广泛存在,并会影响多种元学习算法。
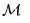 , 任务内训练数据
, 任务内训练数据 和输入
和输入
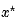 。因此如果能够控制来自
。因此如果能够控制来自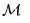 和
和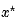 的信息,同时要求实现精确预测,就可以鼓励模型利用
的信息,同时要求实现精确预测,就可以鼓励模型利用 中的信息而不是忽略它。利用信息不等式和PAC-Bayes理论,我们得出一种方式是利用信息瓶颈(information bottleneck)约束:
中的信息而不是忽略它。利用信息不等式和PAC-Bayes理论,我们得出一种方式是利用信息瓶颈(information bottleneck)约束:
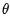 对应编码器 (encoder):
对应编码器 (encoder):
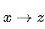 的参数。将以上元正则项 (Meta Regularization)和Model Agnostic Meta-Learning (MAML),Conditional Neural Process (CNP) 相结合, 我们提出了新的 “MAML先生” (MR MAML) 和 “CNP先生” (MR CNP) 算法。在几个非互斥任务的数据集上,我们的算法实现了大幅度的性能提升。在一个3D物体方向预测数据集上我们进行了实验:
的参数。将以上元正则项 (Meta Regularization)和Model Agnostic Meta-Learning (MAML),Conditional Neural Process (CNP) 相结合, 我们提出了新的 “MAML先生” (MR MAML) 和 “CNP先生” (MR CNP) 算法。在几个非互斥任务的数据集上,我们的算法实现了大幅度的性能提升。在一个3D物体方向预测数据集上我们进行了实验:
-
记忆问题广泛存在于元学习问题和元学习算法中 -
记忆问题是一种任务层面的过拟合,这不同于传统上数据点层面的过拟合 -
通过元正则方法我们有效地控制了记忆问题,并拓展了元学习的应用场景
疫情严重,ICLR2020 将举办虚拟会议,非洲首次 AI 国际顶会就此泡汤
疫情影响,ICLR 突然改为线上模式,2020年将成为顶会变革之年吗?
火爆的图机器学习,ICLR 2020上有哪些研究趋势?
1、直播
回放 | 华为诺亚方舟ICLR满分论文:基于强化学习的因果发现
03. Spotlight | 组合泛化能力太差?用深度学习融合组合求解器试试
04. Spotlight | 加速NAS,仅用0.1秒完成搜索
05. Spotlight | 华盛顿大学:图像分类中对可实现攻击的防御(视频解读)
06. Spotlight | 超越传统,基于图神经网络的归纳矩阵补全
07. Spotlight | 受启诺奖研究,利用格网细胞学习多尺度表达(视频解读)
4、Poster
01. Poster | 华为诺亚:巧妙思想,NAS与「对抗」结合,速率提高11倍
 点击“
阅读原文” 查看 ICLR 系列论文解读
点击“
阅读原文” 查看 ICLR 系列论文解读