回想起那时的岁月, 那时的《数学女孩》

生日快乐,我的国

今天介绍的《数学女孩1+2+3》会在翻译组正式成员内进行赠书, 将好书送与支持 [遇见数学] 的朋友们!
发现数学之美, 传播数学文化, 请加入[翻译小组], 更有积分兑换周边/图书及不定期福利, 申请链接.

在动人的故事中走近数学
在青春的浪漫中理解数学
下文节选自《数学女孩 1》, 已获出版社授权许可, [遇见数学] 特此表示感谢!
数学女孩
回忆高中时候
在这样一个春色满园,樱花飘落的地方,她显得有些格格不入。她有着一头乌黑亮丽的秀发,宛若指挥家般修长的手指,温暖的小手,淡淡的清香。
哈哈
第1个個故事
The first tory
白
1
樱花树下的邂逅

那是高一的春天。
开学典礼那天,春光明媚。
输12
开学典礼结束后,我在回教室的途中悄悄地溜了出来,独自一人漫步在校内的樱花树林间。周围连个人影都没有。
我现在 15 岁。15 岁、16 岁、17 岁……毕业的时候我将 18 岁了。有一个 4 次方的数字和一个质数。
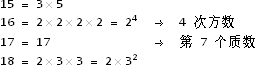
现在教室里同学们一定正进行着自我介绍。我不擅长自我介绍,究竟该说说自己的什么呢? “我喜欢数学,兴趣是讨论计算公式。请多多关照。”
算了,管他呢。静静地上课,在谁都不会去的图书室学数学,就这样像初中时一样度过高中三年的时光吧。
映入眼帘的是一棵硕大的樱花树。
树下站着一个少女,她正抬头仰望着那棵樱花树。
输入
樱花树模模糊糊的花色遮住了天空
一阵风,飘舞着的樱花花瓣将少女裹住
少女也看到了我。
她身材高挑,长发乌黑亮丽,嘴巴紧闭着,一副认真的表情。脸上架着副金丝眼镜。
她清楚地念着:“1, 1, 2, 3”
念完这 4 个数字之后,少女便不出声了,用手指着我,好像在说:“喂!你,请回答接下来的数字。”
我指着自己:“要我回答?”
她没有说话,而是点了点头。食指仍然指向我。
我回想她刚才的题目:“1, 1, 2, 3。”
啊,原来如此。我知道了。
“1, 1, 2, 3 的后面接着的数字是 5,接下来是 8,再接下来是 13,然后是 21,然后再是……”我开始滔滔不绝地回答。
她向我伸出手掌,示意我不要说了。
她又指向我。这是在考我吗?
“1, 4, 27, 256。”
我突然一下子找到了规律。
我回答说:“1, 4, 27, 256,接下来是 3125 吧,再接下来是……心算是不行了。”
她听到我说“心算是不行了”之后神色显得有些不满,摇了摇头,便告诉了我答案。
“1, 4, 27, 256, 3125, 46656, ... ”她的声音很响亮。
她闭上眼,
头微微朝上抬起,
好似正在仰望樱花树。
食指朝着天空飞快地写着些什么
输12
她朝我这里看了看。
又是 4 个数字。
“6, 15, 35, 77。”
我心想,这题好难啊。我开动脑筋拼命思考,
我瞟了她一眼,樱花树下的女孩还笔挺地站在那里,很认真地看着我,甚至都不掸一下飘落到头发上的樱花花瓣。那副认真的模样仿佛是在考试一样。
“啊,我知道了。”
我刚一说,她顿时变得神采奕奕,微微一笑。
我第一次看到她笑,便情不自禁地大声回答:
“6, 15, 35, 77 的后面是 133。”
她摇了摇头,长发飘动,花瓣也随之飘落。她的表情仿佛在说:“哎呀呀,真可惜。”
“计算错误!”她的手指碰了下眼镜。
计算错误?啊,真的算错了。11 乘以 13 应该是 143,而不是 133。
她又继续出了下一题: "6, 2, 8, 2, 10, 18".
这次是 6 个数字。我考虑了一下,最后一个 18 最令人头疼,如果是 2 就好了,现在的数字看上去乱七八糟,没有规则。啊,不对,这些都是偶数。——我知道了!
“接下来是 4, 12, 10, 6, ... ,这道题真伤脑子。”我说道。
“是吗?但你不是解出来了嘛。”
她装模作样地说着,走向我伸出手。她的手指又细又长。
我心想:难道她要和我握手吗?
于是,我莫名其妙地握住了她的手。她的手又柔软又温暖。
“我叫米尔嘉,请多多关照。”
这就是我和米尔嘉的邂逅。
空白
夜晚自己家中
一晃动心儿就潮潮的

女孩啊,女孩
输入
我喜欢夜晚。家人入睡后,我就可以有大量自由的时间,拥有一个没人打扰的世界。我喜欢自己一个人度过那段时间,打开书,探索世界。我思考数学问题,闯入那深邃的密密层林。在那里,我发现了珍稀动物、清澈得令人吃惊的湖,还有需要抬头仰望的大树。令我意想不到的是,还遇到了美丽的花朵。
她就是米尔嘉小姐。
第一次见面就和我进行那样的对话,她真是个奇怪的女孩。她一定非常喜欢数学吧。她连开场白都没说,就直接给我出数列的脑筋急转弯题,简直像考试一样。我是不是合格了呢?我握了她的手,那柔软的手,飘着淡淡的清香,真的是很淡的清香——女孩独特的香味。
我摘下眼镜,把它搁到书桌上,闭上眼睛,开始回想我和米尔嘉之间的对话。
一开始的题目“1, 1, 2, 3, 5, 8, 13, ... ”是斐波那契数列。1, 1 后面的数字是将前两个数字相加,所得的和成为接下来的数字。
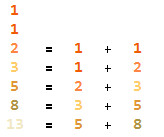
第二道题“1, 4, 27, 256, 3125, 46656, ... ”则是下面这种数列。
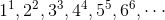
第三道题“6, 15, 35, 77, 143, ... ”的数列如下。
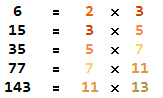
也就 是“质数 × 后一个质数”的形式。可是我把 11 × 13 算错了,真是丢脸啊。米尔嘉一针见血地指出了我的“计算错误”。
最后一道题是“6, 2, 8, 2, 10, 18, 4, 12, 10, 6, ... ”。这道题很难。因为这个数列其实是由圆周率 π 中的每位数字乘以 2 而得到的。

解这道题必须要背出圆周率 π 的各位数字。如果脑海里没有这样一个数列模式,就无法解出这道题。
记忆啊。
我喜欢数学。比起记忆背诵,我更喜欢思考。追溯过去不是数学,发掘新东西才是数学。如果是要背诵的话,只要靠脑子死记硬背就可以了。记人名、记地名、背单词、背元素符号等,这些都无法进行推理计算。但是,数学却不同。一旦告诉我题目后,我就会把材料和道具(笔和纸等)都排列到桌上。我一直认为数学不是靠记忆,而是靠思考。
但是,我又突然觉察到数学也许不是那么简单的东西。
米尔嘉在出“6, 2, 8, 2”这道题时,为什么不单单说“6, 2, 8, 2”,还一直说到“6, 2, 8, 2, 10, 18”呢?那是因为如果她只说“6, 2, 8, 2”的话,我们无法发现其中的规律其实是圆周率 π 的各位数字的 2 倍。我们还可能得出其他简单的答案。假设题目只是“6, 2, 8, 2, 10, ... ”的话,我们还可能联想到以下数列。
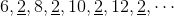
有这样的联想也是非常自然的吧。也就是说,在连续的偶数之间放入一个 2 作为间隔。
原来米尔嘉在出这道题时想得如此周密啊。
“但你不是解出来了嘛。”
她似乎预料到我能够解出这道题。我突然想到她那装模作样的表情。
米尔嘉啊。
在这样一个春色满园,樱花飘落的地方,她显得有些格格不入。她有着一头乌黑亮丽的秀发,宛若指挥家般修长的手指,温暖的小手,淡淡的清香。
不知怎么的,我一直想着米尔嘉的事情。
......
图|来源于网络
☟ 点击【阅读原文】进一步查看或购买此书







