感知概率

本文节转自科学网蒋迅老师博客, 感兴趣的朋友还请 [阅读原文] 移步阅读.

关于作者蒋迅老师及著作

蒋迅, 本科和硕士毕业于北京师范大学, 在美国马里兰大学获得博士学位. 目前在美国从事科学计算工作. 曾应北京师范大学张英伯教授邀请. 在科学网开办了关于数学文化的个人博客 (blog.sciencenet.cn/home.php?mod=space&uid=420554). 与王淑红著《数学都知道》(链接)

向上滑动阅览目录 

【第一册】：

第一章  雪花里的数学

第二章  路牌上的数学、计算游戏Numenko和幻方

第三章  钟表上的数学与艺术

第四章  数学家与音乐

第五章  数学与音乐

第六章  调音器的数学原理

第七章  漫画和数学漫画

第八章  xkcd的数学漫画

第九章  画家蔡论意的数学情缘

第十章  埃拉托斯特尼筛法：从素数到雕塑

第十一章  把默比乌斯带融入到生活中

第十二章  克莱因瓶不仅存在于数学家的想象中

【第二册】：

第一章  乘法口诀漫谈

第二章  奥巴马和孩子们一起计算白宫椭圆办公室的焦距

第三章  用数学方程创作艺术

第四章  说说圆周率p

第五章  根号2，人们发现的第一个无理数

第六章  对数和对数思维

第七章  切割糕点问题

第八章  帮助美国排列国旗上的星星

第九章  美妙的几何魔法\[HorizontalLine]高立多边形与高立多面体

俄国天才数学家切比雪夫和切比雪夫多项式

第十一章  万圣节时说点与鬼神有关的数学

第十二章  美国的奥数和数学竞赛

第十三章  美国的数学推广月

第十四章  地球数学年

第十五章  需要交换礼物的加德纳会议

【第三册】：

江湖中流传的犹太问题

第二章  制造一台150年前设计的差分机

第三章  霍尔和快速排序

第四章  数学对设计C++语言里标准模板库的影响

第五章  再向鸟儿学飞行

第六章  发电的优化管理与线性规划

第七章  关于牛顿-拉弗森方法的一个注和牛顿分形

第八章  爱因斯坦谈数学对他创立广义相对论的影响

第九章  斯蒂芬问题和自由边界问题第十三章

第十章  现代折纸与数学及应用

第十一章  终身未婚的数学家

第十二章  墓碑上的数学恋歌

第十三章  把数学写作当作语言艺术的一部分

第十四章  推介陶哲轩的数学博客

第十五章  杨同海的数学与人生

 

谢尔曼·肯特（Sherman Kent）是耶鲁大学历史学教授。但是在二战和冷战期间，他先后在美国战略情报局和中央情报局工作，共达17年。他的工作是为美国总统提供国家情报评估（National Intelligence Estimate）。在工作中，他总结开创了许多情报分析（Intelligence analysis）的方法。他的一个重要贡献之一就是他为美国中央情报局写的“Words of Estimative Probability”。

我们平时在交谈中会使用“可能”、“很可能”、“极有可能”、“大概”、“不肯定”、“不太可能”等等不明确的词语来描述一个事件的可能性。其实我们给出的是一种没有量化的估计。我们在向上司提交报告的时候，往往也会用到这些词汇。这对上司来说就是一个麻烦，因为不同的人在说“很可能”的时候不一定是相同的意思。所以上司就无法根据我们的报告来做出决断。这对於像国家政府机构来说就是一个致命的问题。

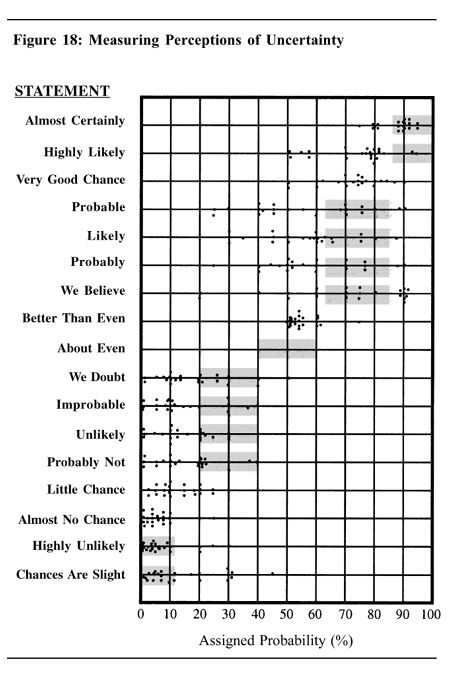
一个解决办法就是量化这些含糊不清的用语。比如说，“可能”就意味着50%的概率，“很可能”就意味着70%的概率，而“不太可能”就是30%的概率。有人可能会认为，“很可能”应该是75%的概率。於是我们可以想像，对於每个定性的词语，它相应的的是一个区间。肯特做过一个统计调查。他将得到的数据做成了下图，并给出了他认为的每一个用词所代表的区间。显然，实际的数据距离他提议的区间还是有所不同的。

Source: Sherman Kent

北大西洋公约组织（NATO）的23名军官们也做了一次类似的统计。下面是他们通常对相应词汇的数值化的理解。表中也包含了肯特提议的区间。似乎他们的回答比肯特找的人更加离谱。比如有5个NATO军官认为“better than even”是47-49%。不知道是否是文化上的差异或语言上的差异造成的。

Source: Critical Thinking For Strategic Intelligence

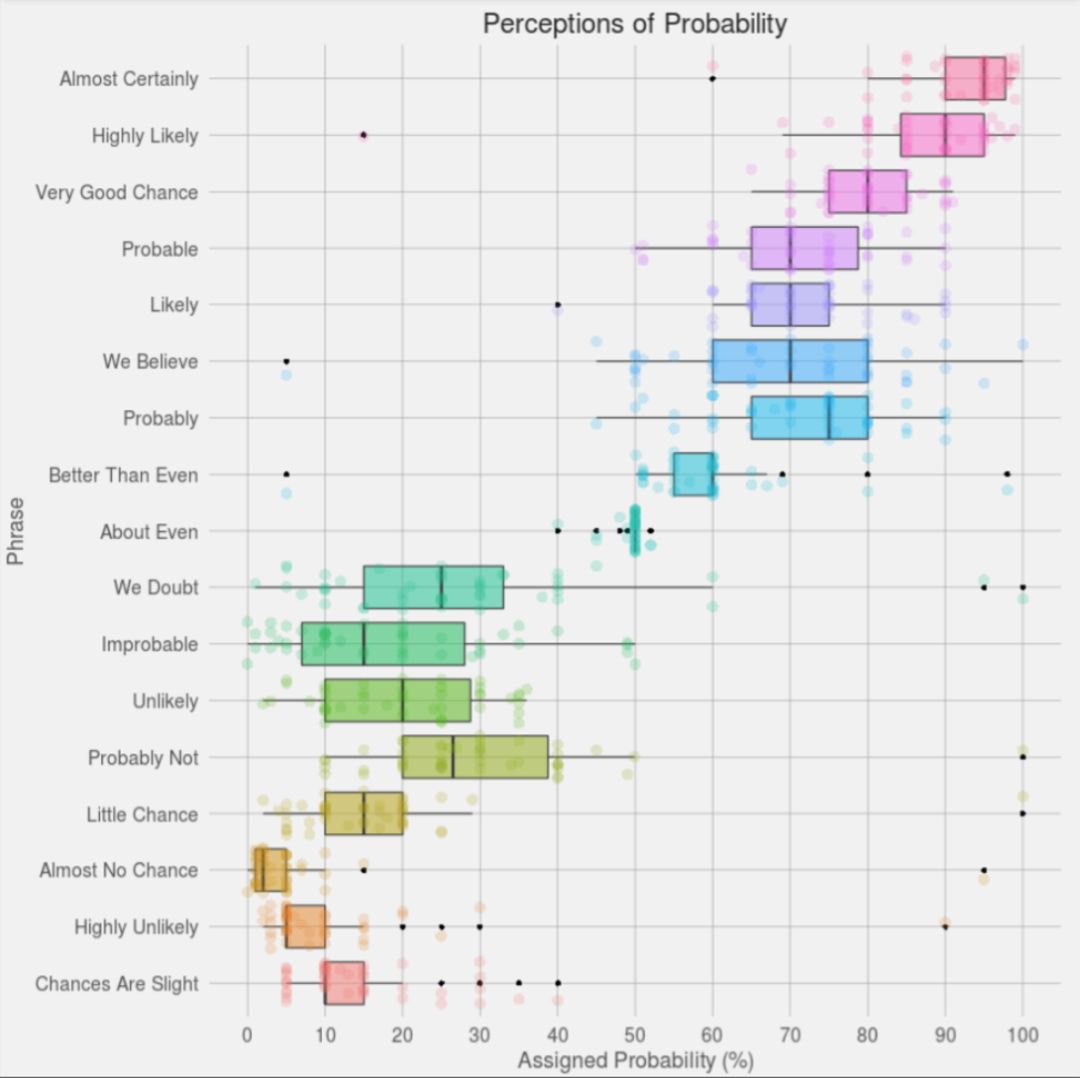
肯特的提议还有一个问题：他给出的区间似乎过於简单。比如，他把“probably”、“likely”、“probably”和“we believe”的区间都定义为同一个区间（从图片上看大约是62-85%）。一方面，这四个词的含义多少有些区分，而且一个从62%到85%的范围也不够精细。有人在reddit上重新做了一次统计（原始数据在这里：raw CSV data (numbers)），然后用R语言程序计算出每个短语的箱形图（box plot），再用ggplot2绘图包制作出漂亮的图表。对这位作者zonination的R程序感兴趣的请点击这里。

Source: KANTAR Information is Beautiful

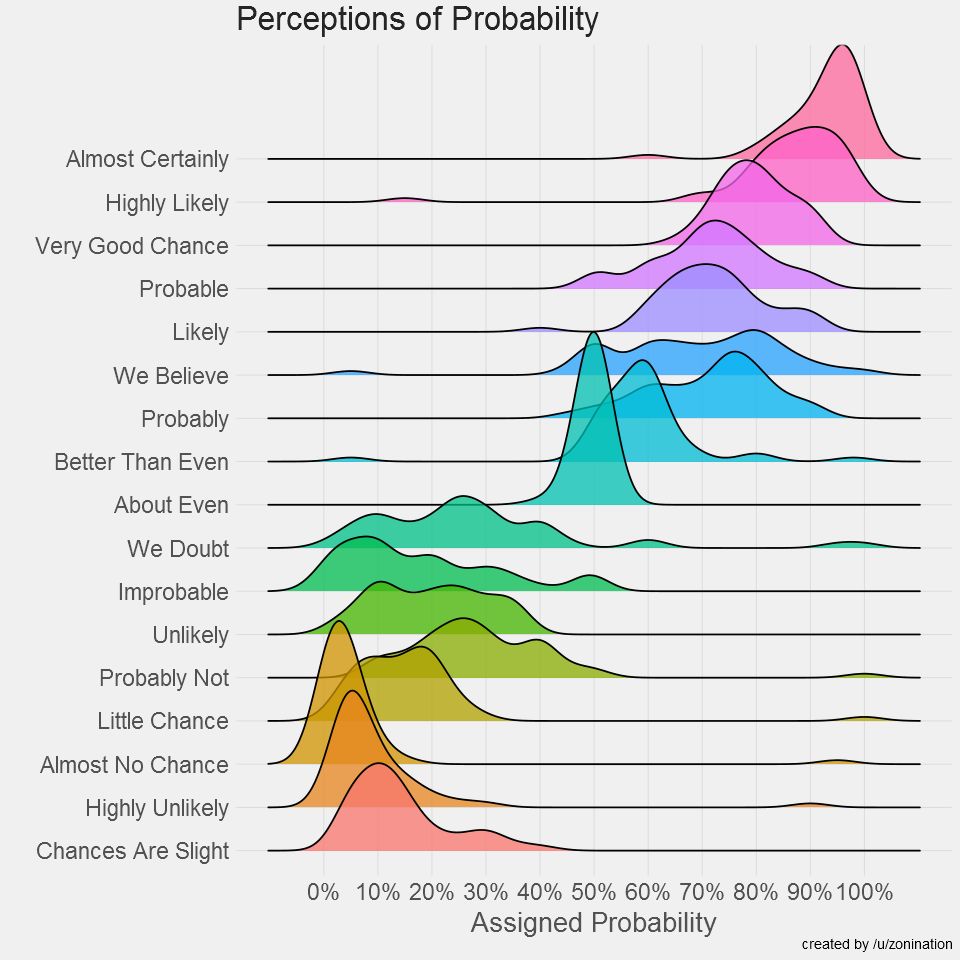
我们看到，这个图表与肯特的提议非常吻合，但是更加精确，也包含了更多的信息。箱形图给出了四分位间距，也给出了中间值的位置。离群值也都清楚地标出了。下面是对同一组数据做出的统计分布图，跟生动。我们看到意见最一致的是对“about even”的理解。我们看到的是一个方差很小的正态分布（那里的离群值让人无语）。

作者保留了全部数据，即使一些明显错误的答案也没有删除。该不该保留其实作为一个练习来说也无关紧要，但如果是提供给政府部门的报告则是一个需要考虑的问题。

Source: KANTAR Information is Beautiful

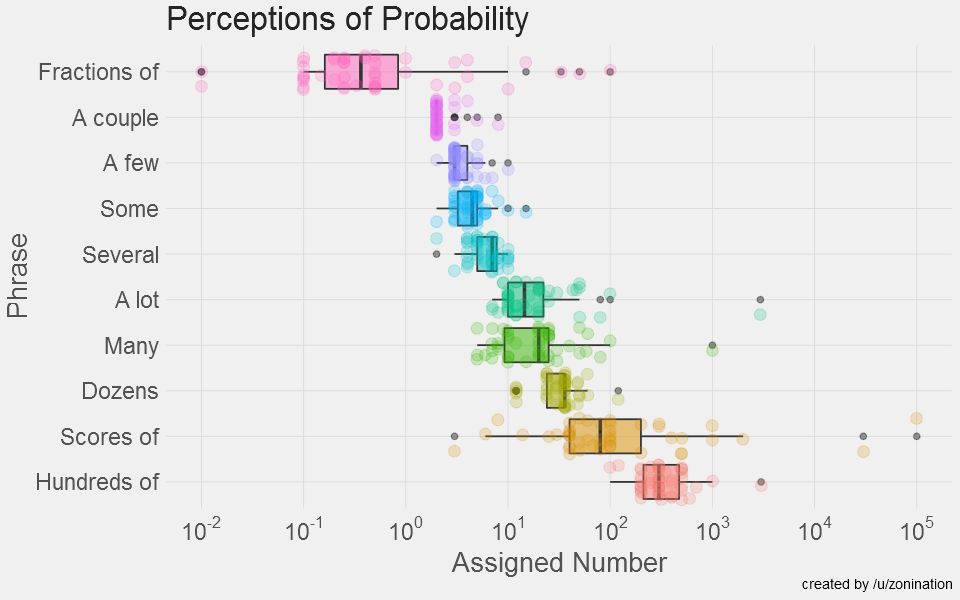
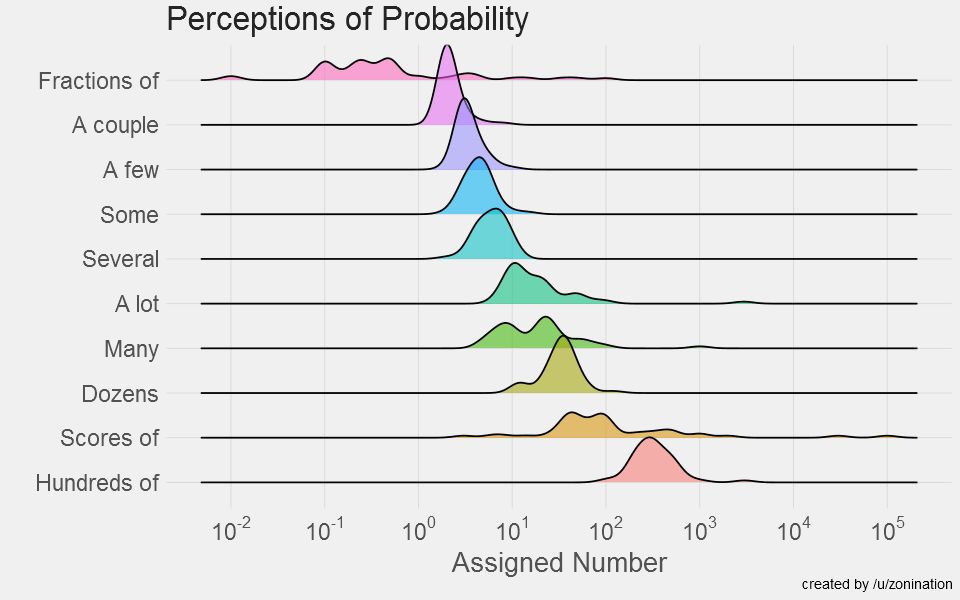
在此基础上，该作者又制作了另一组数据的感知图。如下。这里就不细说了。

Source: KANTAR Information is Beautiful

Source: KANTAR Information is Beautiful

这里的感知还存在缺陷。对同一个用词，在不同的背景里可能有不同意思。在中文中完全同样的词语也有可能是不同的意思。另外，上面的作图中没有去掉明显的“outlier”，这也是值得商榷的。我们在这里仅仅是作为对数据的欣赏而展示给大家，这正如它的出处：Reddit上的“dataisbeautiful”(www.reddit.com/r/dataisbeautiful/)。如果你喜欢数据，不妨到这里寻求数据之美。(完)

「予人玫瑰, 手留余香」感谢支持!