这本数学书AI圈都在转，资深ML研究员历时7年之作，免费电子版可看

羿阁 发自 凹非寺
量子位 | 公众号 QbitAI

这几天，一本免费数学教程在机器学习圈被疯转。

这本书名叫《概率数值》（Probabilistic Numerics），作者是来自马普所、牛津大学和INRIA的三位机器学习大牛，其中一位的谷歌学术引用量达到17000+。

Philipp Hennig、Michael A. Osborne和Hans P. Kersting三位作者在写这本书时，前后一共写了7年，长达400多页。

新书发布后，作者之一Philipp Hennig在推特上感叹：它终于出来了。

除了实体出书以外，作者们也在网上分享了全书的免费电子版。（ps:文末可以查看~）

具体来说，这本书希望从数学的角度，教会大家如何优化机器学习模型。

通常，机器学习涉及大量线性代数、积分、或寻找非线性函数的最小值等问题，而这些问题往往会占用大量计算资源。

因此，作者希望能通过讲解背后概率数值计算的原理，让我们理解模型“耗能的原因”，从而更好地优化模型。

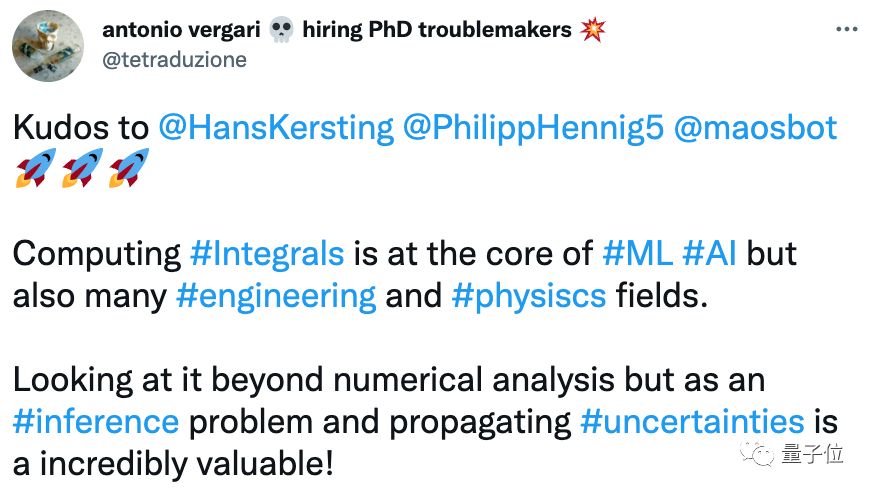
对于这本书，爱丁堡大学机器学习讲师Antonio Vergari点了个赞：

数值计算积分不仅是机器学习、人工智能的核心，也是工程、物理等领域的核心。

除了数值分析的角度，从模型推理和传播不确定性等领域来看，也是非常有价值的。

这本书有什么用？

在计算机中，有很多问题涉及复杂系统的求解。

例如用计算机预测天气、癌细胞基因突变等问题，都与复杂系统有关，由于这种系统在求解时容易引入不确定性，又会导致计算资源的浪费。

而在机器学习中，模型给出的预测结果不一定是可靠的，各种因素也会导致输出结果的不确定性。

目前，随着数据精度的提升，不确定性带来的计算量也还在进一步增大。

从数学角度来说，如何量化这种不确定性、降低计算资源的浪费，就涉及概率数值（概率统计、数值分析等）的理论和方法。

如果能掌握它的理论技巧，计算机就能更高效地处理数据，还能利用这种不确定性来做出计算的最优决策，包括使用贝叶斯推断等理论，来构建更灵活、更高效、更个性化的算法。

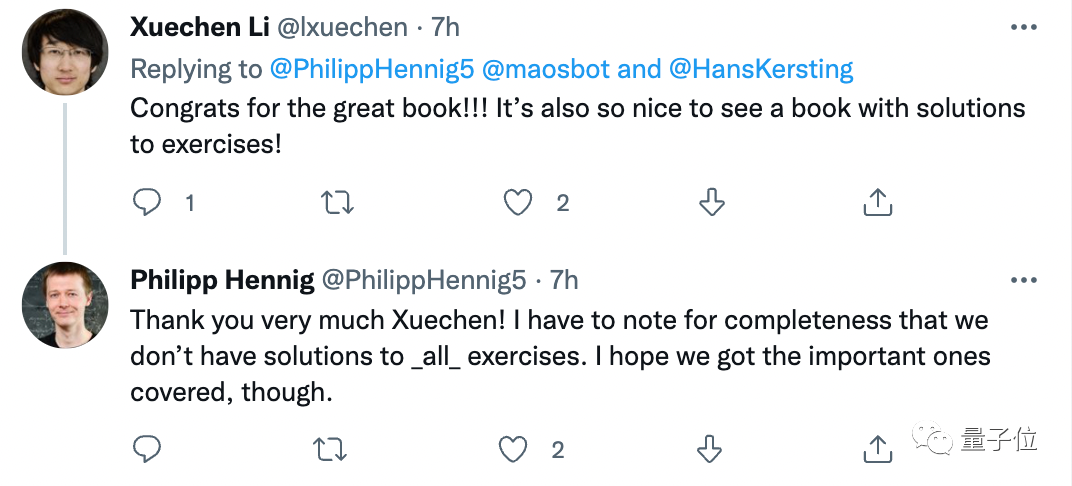
在书中，作者不仅充分讲解了概率数值计算的原理，还进一步通过练习题手把手地教你如何优化一个机器学习模型，并且所有重要的练习都配备了解决方案。

这一点获得了网友的点赞。

正如作者在简介中所说：

我们为所有需要使用数值计算的人写了这本书，不管是天体物理学家还是深度学习黑客。

对于那些正在或正打算成为数值计算领域开发者的人，以及正在学习机器学习的人，我们希望这本书会是有趣的。

这本书讲了什么？

在机器学习快速发展的当下，这本书旨在给新兴的概率数值领域做一个概述。

书中内容主要从以下几方面展开：

1、数学基础

概率数值计算是机器学习和应用数学之间的桥梁，要想学会机器学习，数学是绕不开的话题。

这一章节对后续会使用到的概率推理、高斯函数、回归、线性代数等关键概念进行了介绍。

有统计学或机器学习背景的读者读起来会很轻松～

2、积分

本章利用积分的基本概念，介绍了概率数值计算的核心——贝叶斯积分公式、经典求积公式等理论，并重构现有的数值求积规则，在现有的方法上开发新的功能。

3、线性代数

线性代数运算，可以说是最基本的数值计算。与矩阵运算、向量运算一样，它们几乎是当代计算机领域所有重量级运算的基石。因此，这一领域的研究非常深入。

首先，你需要了解一些线性代数的基础知识——向量化矩阵、克罗内克积、正定矩阵、弗罗贝尼乌斯矩阵范数等等。

其次，书中致力于培养对线性代数的直觉理解，这有助于我们更好地理解数学的本质、看懂复杂公式背后最简单的套路。

4、局部优化

在数值计算过程中，如果建模不当会导致很多问题，这点在深度学习等领域格外明显。

本章重点关注非线性优化问题，以步长选取为例进行讲解。

5、全局优化

本章介绍一个很有效的全局优化算法——贝叶斯优化，该方法可以不受限制地解决计算成本高、导数未知的问题，并且能够在尽可能少的步骤中找到全局最小值。

6、常微分方程解法

在研究常微分方程的过程中，我们需要辩证看待常微分方程和偏微分方程的关系，并且需要适时将其进行转化。这样，我们才能灵活求解常微分方程。

本章主要从经典的ODE求解器、ODE滤波器和平滑器等方面进行讲解。

7、前景

概率数值的未来是广阔的，该领域中的许多基础数学、工程和哲学问题仍有待解决。在本章中，我们将重点讨论一些可能至少影响学术界未来十年发展的开放性问题。

8、练习&答案

除了上述的文字资料外，本书还提供了许多附带解决方案的练习题。

三位作者都是谁？

作者之一的Michael A. Osborne昨天在推特上分享道“我们从2015年开始写这本关于机器学习的新计算基础的书，现在它像我的孩子一样长大了”。

Michael A. Osborne，牛津大学机器学习教授，也是Mind Foundry有限公司的联合创始人。

Osborne专注于机器学习领域中的主动学习、贝叶斯优化和贝叶斯积分等方向，而且热衷于新兴的概率数值领域。

Philipp Hennig，蒂宾根大学机器学习方法教授，同时也是MPII（马克斯·普朗克智能系统研究所）的兼职研究员，ELLIS(欧洲学习和智能系统实验室)学习机器理论、算法和计算研究项目的联合主任。

在他的职业生涯中，概率数值方法是主要的研究方向之一。Hennig的研究得到了艾米·诺特(Emmy Noether)、马克斯·普朗克(Max Planck)和ERC奖学金的支持。

Hans P. Kersting，INRIA（法国国家信息与自动化研究所）和ENS（巴黎高等师范学院）的博士后研究员，从事机器学习方面工作，主要研究方向是贝叶斯推理、动态系统优化等。

最后附上作者提供的《概率数值》免费电子版，感兴趣的小伙伴赶紧一睹为快吧！

《概率数值》：https://www.probabilistic-numerics.org/assets/ProbabilisticNumerics.pdf

— 完 —

「人工智能」、「智能汽车」微信社群邀你加入！

欢迎关注人工智能、智能汽车的小伙伴们加入我们，与AI从业者交流、切磋，不错过最新行业发展&技术进展。

ps.加好友请务必备注您的姓名-公司-职位哦~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~