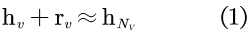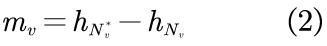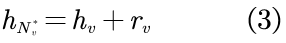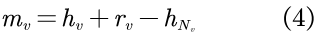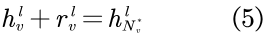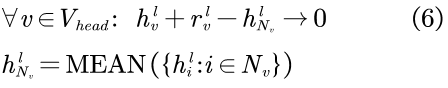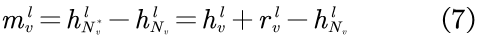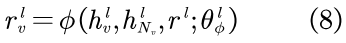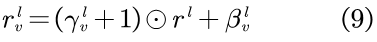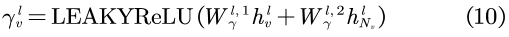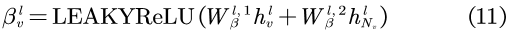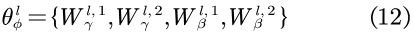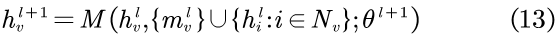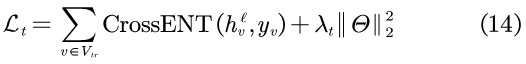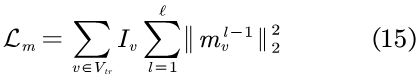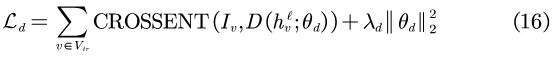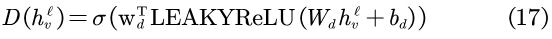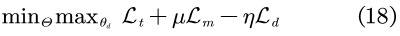KDD'21 | 图神经网络如何建模长尾节点?
Tail-GNN: Tail-Node Graph Neural Networks
KDD 2021
01
—
02
—
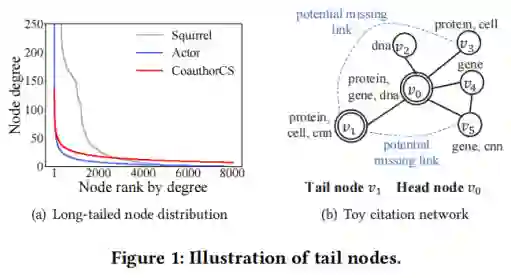
相关定义
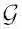 ={V,
={V,
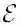 ,X},对于每个节点v∈V,定义N
v
表示节点v的邻居节点集合,也被称作邻域,而|N
v
|则为节点v的度。同时,定义V
head
与V
tail
分别表示头、尾结点。对于阈值K,尾结点的度不超过K,即V
tail
={v:|N
v
|≤K},而头结点则作为尾结点的补充,即V
head
={v:|N
v|
>K}。本文将K视为预先设定的超参数。
,X},对于每个节点v∈V,定义N
v
表示节点v的邻居节点集合,也被称作邻域,而|N
v
|则为节点v的度。同时,定义V
head
与V
tail
分别表示头、尾结点。对于阈值K,尾结点的度不超过K,即V
tail
={v:|N
v
|≤K},而头结点则作为尾结点的补充,即V
head
={v:|N
v|
>K}。本文将K视为预先设定的超参数。
03
—
可转移的邻域转化
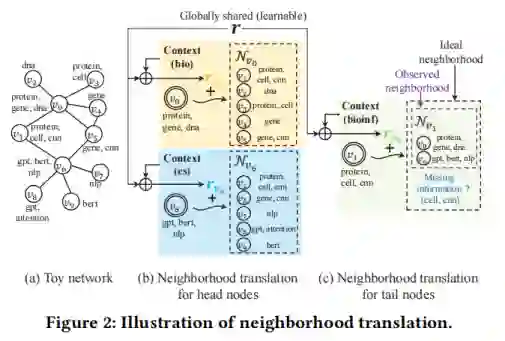
为了增强尾节点的表征学习,本文提出了一种名为邻域转化的新概念,在此基础上,进一步设计了一种从头结点到尾节点的知识转移。具体如图2所示。
通常,节点与其邻居节点之间紧密的结构连接产生了它们之间的联系,特别地,GNN与其他基于图的方法都假定节点与其相邻节点相似。例如,如图2(a)所示,对v0及其邻居,使用生物学关键词来描述,而对节点v6,则使用计算机科学关键词来描述。本文利用转化操作对节点v与其邻域Nv之间的关系进行建模,以模拟邻域中缺失的信息。形式上,设hv表示头节点v的节点嵌入向量,并设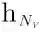
其中,rv为翻译向量,其可以被一个可学习模型预测,该模型在下部分会具体阐述。
3.2 基于头尾转移预测丢失的邻域信息
本文通过将邻域转化的知识从头节点转移到尾节点以发现缺失的邻域信息。
3.2.1 头节点的邻域
由于头节点在图中连接良好,故假设其邻域完整且有代表性,则邻域转化自然存在于头节点及其邻域内。因此,可直接学习模型以预测头节点的转化向量。
3.2.2 尾节点邻域
相反,由于各种原因,尾节点在结构上受到了限制,从而导致了一个小的可观测邻域,即在GNN中,尾节点的观测邻域可能不足以代表有意义的聚合。因此,必须找出尾节点缺失的邻域信息。具体来说,尾节点v的缺失信息,可被mv表示,而mv则由其理想邻域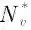
此处,理想邻域不仅包含观测邻域,还包含可以链接到v的节点,理想邻域与观测邻域以及缺失邻域之间的关系如图2(c)所示。
3.2.3 预测缺失信息
为了计算式2,需要首先预测未知的理想邻域表征。具体来说,可以对头节点和尾节点利用统一的转化模型,以得出它们的理想邻域。对于头节点,由于它的观测邻域已经是理想的,故只需学习预测式1中的转化向量rv;而对于尾节点,则为转化模型应用预测模型以构造理想模型,从而将知识从头节点转移到尾节点。可表示为:
其中,转化向量rv由从头节点学习得来的转化模型学习而得到。尾节点的缺失邻域则可表示为:
04
—
Tail-GNN
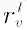 表示第l层中节点v的转化向量,其可以由共享模型构建。而则表示节点v在第l层的理想邻域表示,由于假设v为头节点,故
表示第l层中节点v的转化向量,其可以由共享模型构建。而则表示节点v在第l层的理想邻域表示,由于假设v为头节点,故
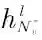 可由
可由
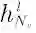 (即同一层中节点v的观测邻域)近似得出,上式可被改写为:
(即同一层中节点v的观测邻域)近似得出,上式可被改写为:
其中,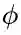
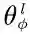
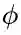
LEAKYReLU被用作激活函数,而所有的W都为一个可学习的权值矩阵,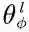
4.3 总体损失
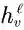 (ℓ为总层数)维度与种类数量相同,并且使用softmax函数作为激活函数。y
v
为单热向量,其对节点v的类别进行了编码。CrossENT为交叉熵函数,Θ包含了Tail-GNN中所有可学习的参数。
(ℓ为总层数)维度与种类数量相同,并且使用softmax函数作为激活函数。y
v
为单热向量,其对节点v的类别进行了编码。CrossENT为交叉熵函数,Θ包含了Tail-GNN中所有可学习的参数。
其中,σ为sigmoid函数,θd={Wd,bd,wd}包含了鉴别器D所有可学习的参数,λd为超参。
4.3.4 总体损失
最后,将所有损失进行集成,表示为:
其中,μ与η为超参数。
05
—
实验
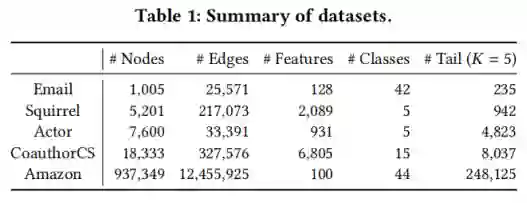
本文使用的数据集如下表所示。
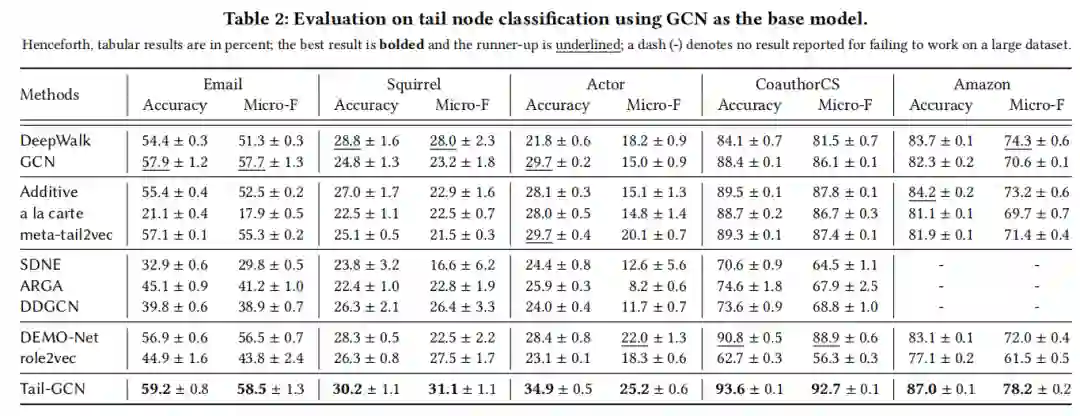
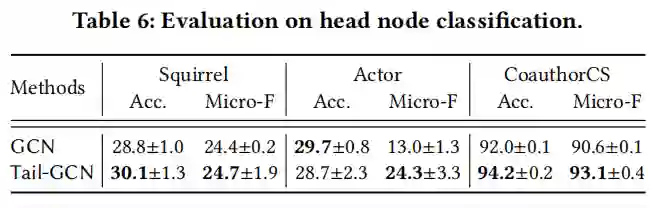
本文模型在尾节点分类任务上的性能如表2表3所示,其中,表2中本文模型以GCN作为基准模型,表3以其他GNN模型作为基准模型。
06
—
总结
原文地址:https://dl.acm.org/doi/pdf/10.1145/3447548.3467276