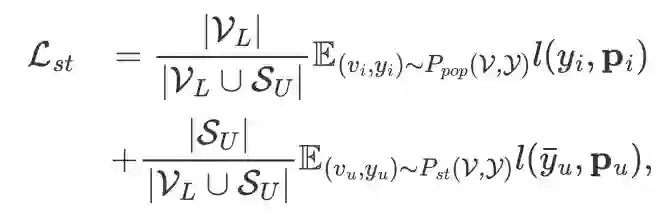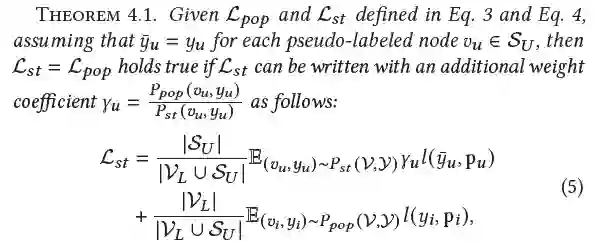会员服务 ·

WWW2022 | 迷途知返：分布迁移下的图神经网络自训练方法

2022 年 2 月 19 日 专知

论文题目： Confidence May Cheat: Self-Training on Graph Neural Networks under Distribution Shift

会议： The WebConf 2022

论文地址 ：

https://www.zhuanzhi.ai/paper/69f3151203666bb9a971078f3cf337e2

1 引言

近几年来，图神经网络（GNNs）得到飞速发展，在多种图相关的任务中性能卓越。众所周知，GNN卓越的性能严重依赖于有标签数据构成的监督信息，而数据标签的获取往往代价高昂。为了解决数据标签的稀疏性问题，自训练策略被引入到图神经网络中。自训练策略是一种利用模型对无标签节点的预测生成伪标签，从而扩充原始训练集的方法。一般来说，为了尽可能过滤掉错误的伪标签，现有的图神经网络自训练方法仅会保留高置信度预测生成的伪标签。然而，预测的高置信度代表模型可能已经学习到了该节点包含的大部分信息，再通过自训练策略将该节点加入到训练集真的是有效的吗？

为了回答上述问题，我们进行了如下两个探究性实验：

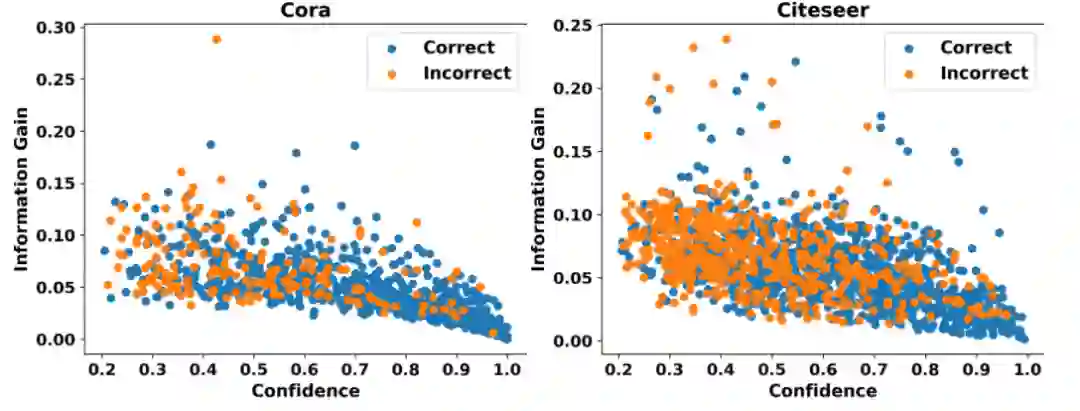
(1) 探究置信度与信息增益的关系 这里的信息增益指对模型参数的信息增益，可以衡量节点为模型引入额外信息的多少，因此该探究性实验可以清楚地展示高置信度节点是否能够为模型引入额外信息。

我们可视化了标准GCN模型对Cora和Citeseer两个数据集中无标签节点的置信度与节点对模型参数的信息增益的关系，如图1所示，其中横坐标代表置信度，纵坐标代表信息增益，蓝色与橙色的点分别代表预测正确与预测错误的节点。我们可以清楚地看到，置信度与信息增益呈现明显的负相关关系。也就是说，置信度越高的节点信息增益越低。考虑到现有的图神经网络自训练方法仅会保留高置信度预测生成的伪标签，我们认为这些方法难以为模型引入额外的有效监督信息。为了进一步解释上述现象存在的原因，我们又进行了如下实验。

图1 置信度与信息增益的关系

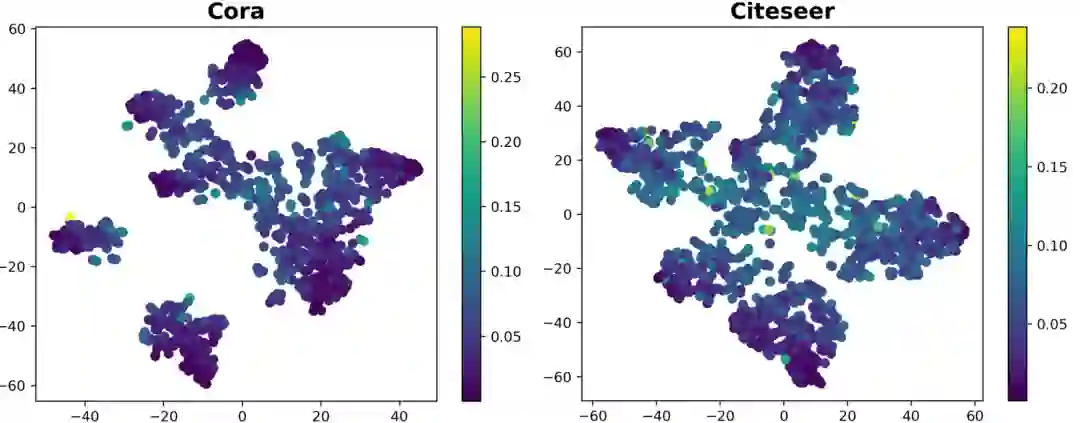
(2) 探究节点嵌入表示的分布情况 本质上来讲，图神经网络自训练策略通过为模型引入额外的监督信息，使模型实际的决策边界更靠近最优决策边界，从而获得更好的性能，因此我们希望该额外的监督信息分布于靠近决策边界的位置，从而能够最大程度地影响到决策边界的改变。基于上述分析，我们可视化了节点嵌入表示（embedding）的分布，对置信度与决策边界的关系做进一步探究。

我们利用t-SNE[1]算法可视化了标准GCN模型对Cora和Citeseer两个数据集的嵌入表示（GCN的softmax层的输入），如图2所示，其中颜色越深的点代表该节点对模型参数的信息增益越低。我们发现，大多数的低信息增益（高置信度）的节点都分布于远离决策边界的位置。这一方面解释了为什么这些节点拥有更低的信息增益，另一方面也暗示了现有图训练方法关注的节点大部分远离决策边界。因此，这些节点难以帮助模型获得一个更加有效的决策边界。从这个角度来说，现有的图神经网络自训练方法被置信度“欺骗”到了。

图2 节点嵌入表示的分布

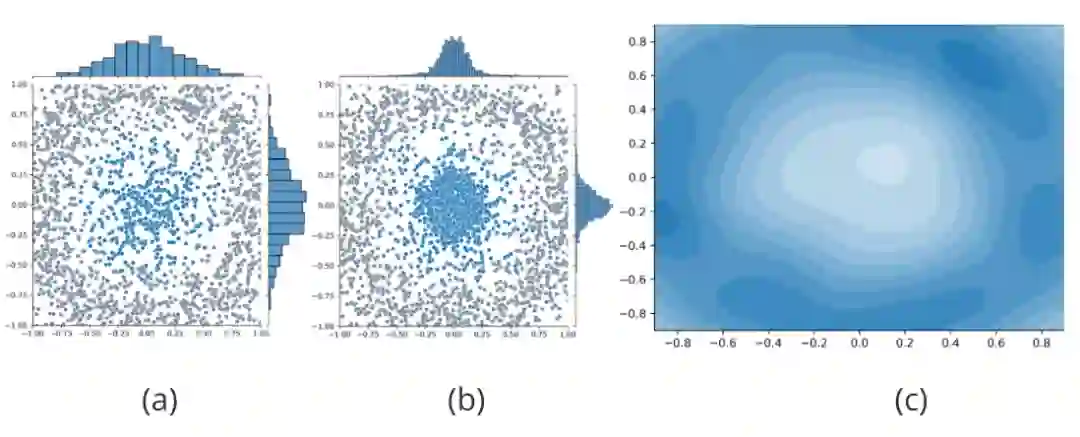
我们进一步分析图神经网络自训练方法被置信度“欺骗”的严重后果。我们用随机生成的500个符合二维高斯分布的蓝色点表示一类有标签节点的嵌入表示，用其余4000个符合圆环分布的灰色点表示其他类有标签节点的嵌入表示，如图3(a)所示。此外，遵循半监督任务的设定，数据集中还存在大量的无标签节点，但是为了示意图的清晰，我们未在其中进行表示。根据现有图神经网络自训练方法的核心思想，GNN模型对位于“蓝色”类中心（远离决策边界）的无标签节点拥有更高的置信度，因此这些节点将会被赋予伪标签并加入到训练集中，而位于决策边界附近的节点将会被置信度过滤掉并不予考虑。这将导致训练集的分布将随着自训练的进行逐渐偏向于类别中心节点所代表的分布，与原始训练集的分布明显不同，如图3(b)所示，出现分布迁移现象。图神经网络自训练方法引入的分布迁移可能会使模型拥有糟糕的泛化能力，严重威胁到模型的性能。

图3 对分布迁移的解释

为了解决上述问题，我们提出了基于分布恢复的图神经网络自训练方法DR-GST。我们首先分析了理想与分布迁移情况下图神经网络自训练方法的损失函数，理论结果表明只要为每个无标签节点赋予适当的权重便可以消除分布迁移问题。基于对实验结果的分析，我们提出利用正则化后的信息增益作为上述权重。此外，为了消除自训练策略可能引入的错误信息，我们将损失修正策略引入到图神经网络自训练方法中。最后的理论分析与实验验证均证明了我们方法的有效性。

2 模型

本节将首先阐述如何使发生迁移的增强数据集的分布恢复成原始数据集的分布，并由此提出一个新型的图神经网络自训练框架DR-GST，接着将损失修正策略引入到DR-GST中，最后对新提出方法的合理性进行理论分析。

2.1 利用信息增益加权的损失函数做分布恢复

我们从图神经网络自训练方法的损失函数入手，逐步分析理想情况下与分布迁移情况下损失函数的异同，由此找到解题之径。首先假设原始训练集服从总体分布，给定GNN分类器，则最优的参数集将通过最小化如下损失函数得到:

其中，和分别代表节点集和标签集，为多分类下的交叉熵损失函数，为分类器输出的第个节点的概率向量。类似地，分布迁移下图神经网络自训练方法的损失函数也可以表示为：

其中，与分别代表原始训练集与图神经网络自训练方法选取的伪标签节点集，为节点的伪标签，为发生分布迁移的增强训练集的分布。

由于图神经网络自训练引入的分布迁移可能会使模型拥有糟糕的泛化能力，严重威胁到模型的性能，因此我们希望参数集通过优化总体分布下的损失函数而不是分布迁移下的损失函数得到。然而实际上，只有是可以为我们所用的。为了解决这个问题，我们提出了如下定理。

简单来说，上述定理指出，只要我们能在计算损失函数时为每一个伪标签节点赋予一个适当的权重系数，就可以使，增强后训练集将等价于没有发生分布迁移。

但是可惜的是，总体分布实际上是不可求的，否则我们可以仅通过采样便可以得到足够多的训练数据，因此权重系数也是不可求的。为了弥补上述不足，我们提出利用信息增益来近似，该近似的合理性可以通过图3(c)进行解释。具体来说，我们在图3(c)中可视化了图3(a)(b)代表的生成数据集中每一个无标签节点需要的权重系数，其中颜色越深的区域代表越大。我们发现，随着节点越来越远离类别中心（靠近决策边界），呈现越来越小的趋势，而这种变化趋势与信息增益的变化趋势（图2）是一致的。上述可视化结果指出，利用信息增益对进行近似是合理的。

2.2 信息增益估计

本小节将详细阐述 graph 中每个节点对模型参数的信息增益的计算方法。

每个节点对模型参数的信息增益如下式所示，

其中代表 Shannon 熵，代表模型参数的后验分布，代表节点的特征，代表邻接矩阵。上式的第一项衡量了在后验下模型参数的信息量，而第二项衡量了当给定一个额外的节点后模型参数的信息量，因此两项相减可以衡量该节点能为模型参数带来信息量的多少，即对模型参数的信息增益。

一般来讲，式(3)中模型参数的后验分布是难以求解的，在传统的贝叶斯神经网络中往往可以使用 dropout 变分推断[2]进行估计。另外，[3] 也提出在graph中也可以使用 dropedge[4] 做变分推断的方式估计。在本文中，我们分别使用了 dropout 和 dropedge 做变分推断。

2.2.1 dropout变分推断

给定一个层GCN模型，其第层的输出可以通过下式计算得到：

其中代表对邻接矩阵的正则化算子，是第(l-1) 层的权重矩阵，是激活函数。dropout本身是一种在训练中通过随机掩盖掉graph中节点的某些特征以提高模型泛化能力的方法，具体来说，加入dropout后第层的输出为：

其中中的每一个元素都服从伯努利分布，为哈达玛积。这种对特征做伯努利随机采样的方式可以等价于对做采样，因此我们可以进行次蒙特卡洛采样以在推断(inference)时对进行估计。但实际上，在GCN的每一层均进行蒙特卡洛采样的策略会带来较大的时间开销，我们对其进行了简化，仅在GCN的最后一层做dropout并进行次采样。因此，在第t次推断时，节点的概率向量可以通过下式得到：

2.2.2 dropedge变分推断

类似于dropout变分推断的方法，加入dropedge后第层的输出为：

相应地，我们也仅在模型的最后一层做dropedge，则第次推断时可以通过下式得到：

2.2.3 估计信息增益

有了每个节点在第次推断时的概率向量，可以通过下式计算信息增益：

其中，每个节点的预测分布通过下式计算：

最后，我们利用上述信息增益对损失函数进行加权。

其中是平衡系数。我们称优化该损失函数的图神经网络自训练框架为 DR-GST。

2.3 利用损失修正策略改进伪标签的质量

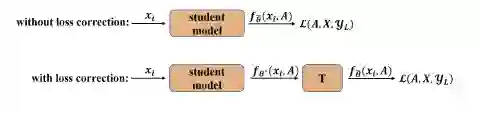
到此为止，我们提出了DR-GST，其利用信息增益加权的损失函数解决了图神经网络自训练引入的分布迁移的问题，赋予了高信息增益的节点更多注意力。然而，高信息增益的节点同样意味着伪标签的高错误率，如图1所示。因此，DR-GST 同样会扩大错误伪标签的影响，为模型训练引入更多不正确的监督信息。基于此，我们提出利用损失修正（loss correction）[5]策略缓解错误伪标签带来的消极影响。

损失修正策略的核心思想：给定某个在完全正确的监督信息下训练得到的模型，以及一个通过伪标签训练集训练得到的模型，假设存在一个预先学习好的转移矩阵，使得可以表示为，则我们可以通过对做训练得到。加入损失修正策略的模型如图4所示。关于损失修正策略的理论分析以及转移矩阵的计算请参见原文。

图4 损失修正策略

本文到此为止完整地阐述了提出的新型图神经网络自训练框架DR-GST，其算法伪代码如图5所示。

图5 DR-GST算法伪代码

2.4 对DR-GST合理性的分析

本节将对图神经网络自训练算法的影响因素进行分析，并进一步推出 DR-GST 设计的合理性。

对于图神经网络自训练算法的影响因素，我们有如下定理：

具体来说，我们从梯度下降的角度进行了分析，结论指出，自训练方法的性能与数据集总体分布和增强训练集分布的差异，以及伪标签的错误率呈负相关。与此同时，我们提出的DR-GST框架恰好通过信息增益增强的加权函数修正了增强训练集的分布，并通过损失修正策略缓解了错误伪标签的消极影响。这证明了DR-GST的合理性。

3 实验

本节将利用节点分类任务，从实验的角度证明 DR-GST 对改进模型性能的有效性。

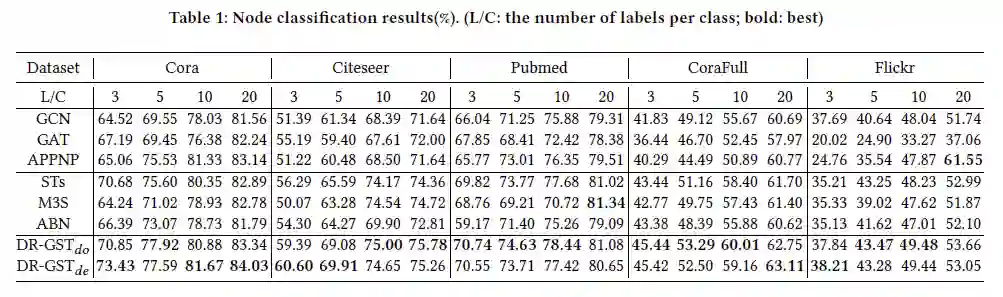
我们选取了五个常见的数据集Cora、Citeseer、Pubmed、CoraFull、Flickr，选择了3、5、10、20等四个标签率，与3个有代表性的GCN方法与3个图神经网络自训练框架进行了对比。实验结果如下图所示，其中与分别代表利用 dropout 和 dropedge 做变分推断的变体方法。可以发现，DR-GST 几乎在所有设定中有最好的性能。

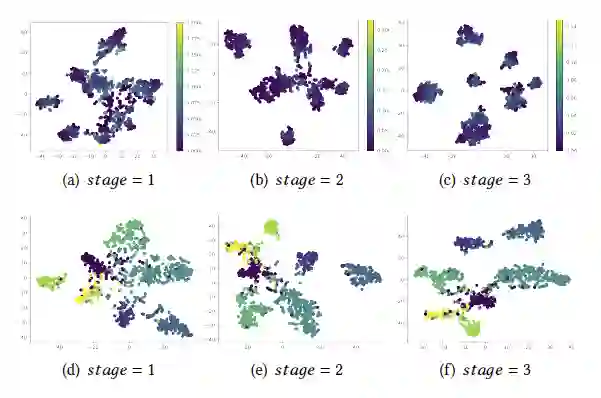
此外，我们也可视化了Cora 数据集中无标签节点((a)-(c))与测试集节点((d)-(f))的嵌入表示的分布情况，如下图所示。可以看到，随着训练的进行，模型对该数据集拥有越来越清晰且有效的决策边界，这从侧面证明了我们方法的有效性。

[1] Laurens Van der Maaten, Geoffrey Hinton. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(11).

[2] Yarin Gal and Zoubin Ghahramani. 2016. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In ICML. 1050–1059.

[3] Arman Hasanzadeh, Ehsan Hajiramezanali, Shahin Boluki, Mingyuan Zhou, Nick Duffield, Krishna Narayanan, and Xiaoning Qian. 2020. Bayesian graph neural networks with adaptive connection sampling. In ICML. 4094–4104.

[4] Yu Rong, Wenbing Huang, Tingyang Xu, and Junzhou Huang. 2019. Dropedge: Towards deep graph convolutional networks on node classification. arXiv preprint arXiv:1907.10903 (2019).

[5] Giorgio Patrini, Alessandro Rozza, Aditya Krishna Menon, Richard Nock, and Lizhen Qu. 2017. Making deep neural networks robust to label noise: A loss correction approach. In CVPR. 1944–1952.

本期责任编辑：王啸

本期编辑：刘佳玮

专知便捷查看