如何理解K-均值的缺陷和假设
编者按:K-均值是一个明晰简单的聚类方法,也不要求关于聚类特征(分类标准)的假定。然而,K-均值仍然对数据分布有一定要求,如果不满足,K-均值就会失败。Stack Overflow数据科学家David Robinson在Cross Validated解释了K-均值的缺陷和隐含的假设,并以此为例展示了检视任何统计学方法的缺陷和假设的方法。
问题
K-均值是聚类分析中广泛使用的方法。我的理解,这个方法不需要任何假设,比如,给我一个数据集和一个预先指定的聚类数值,k,我可以直接应用算法以最小化SSE(聚类内的平方误差)。
因此,本质上K-均值是一个优化问题。
我读过一些讨论K-均值的缺陷的材料。大部分材料是这么说的:
K-均值假设属性(变量)的方差分布具有球形性。
所有变量的方差一致。
所有k个聚类的先验分布是一致的,即每个聚类大致上具备相同数目的观测数据。
以上任何假设不成立,k-均值将失败。
我没法理解这些陈述背后的逻辑。我认为K-均值方法本质上不带任何假设,它只不过是在最小化SSE,我看不到SSE和上面三个“假设”之间的联系
-- KevinKim
开场白
多么好的一个问题——这是一个展示如何检视任何统计学方法的缺陷和假设的机会。换句话说,编造一些数据然后在这些数据上尝试算法!
我们将讨论你的问题中提到的两个假设,看看当这些假设不成立时K-均值会怎么样。我们将使用易于可视化的二维数据。(感谢维度的诅咒,增加额外的维度将加剧而不是减缓这些问题。)我们将使用统计编程语言R:你可以在这里找到全部代码(我同时把这个回答发布在我的博客上)。
题外话:安斯库姆四重奏
首先让我们考虑一个类比。想象一下,有人提出了以下主张:
我读过一些讨论线性回归的缺陷的材料——线性回归期望线性趋势,残差呈正态分布,没有离散值。但线性回归做的不就是最小化到预测线的平方误差的总和(SSE)吗?这是一个优化问题,不管曲线的形状是什么样的,也不管残差的分布是什么样的,这个优化问题总能解决。因此,线性回归不需要任何假设就能工作。
好,是这样,线性回归通过最小化平方误差和工作。但线性回归本身不是回归的目的:我们试图做的是,绘制一条直线,作为基于x预测y的可靠、无偏的预测器。高斯-马尔可夫定理告诉我们,最小化SSE能达到这一目标——这一定理依赖于一些特定的假设。如果这些假设不成立,你仍然可以最小化SSE,但那可能毫无意义。这就像是“你通过踩动踏板驱动汽车:开车本质上是一个‘踏板踩动工程’。不管油箱里有没有油,你都可以踩动踏板。因此,尽管油箱是空的,你仍然可以踩动踏板并开动汽车”。
不过,空口无凭。让我们来看看冰冷坚硬的数据。或者,编造的数据。
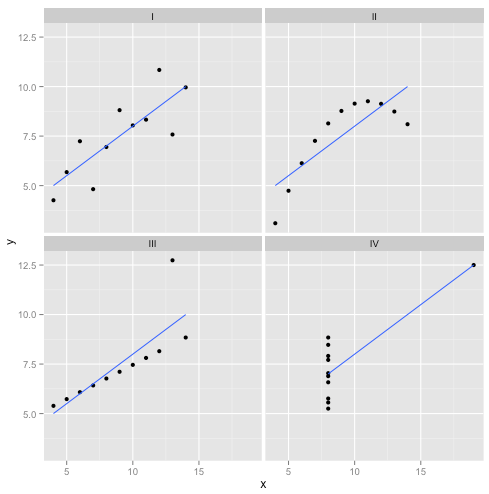
事实上这是我最喜欢的编造数据:安斯库姆四重奏。这些由统计学家Francis Anscombe在1973年创建的混合物表明盲目相信统计方法是如何愚蠢。上面的每个数据集都具有相同的线性回归斜率、截距、p值和R2——然而只需一瞥,我们就能看到只有第一个数据集适用于线性回归。第二个数据集的线性回归形状不对,第三个数据集的线性回归因为单个离散值而歪斜,第四个数据集明显不具备任何趋势!
有人可以说“在这些情形下,线性回归仍然工作,因为它最小化了残差的平方和”。但这只是皮洛士式胜利!(译者注:皮洛士式胜利是一句西方谚语,伊庇鲁斯国王皮洛士于公元前280年左右在两次战役中战胜了罗马,但罗马能在战斗结束后马上补充兵员,而海外作战的皮洛士却迟迟得不到兵力补充,故而两次胜利并未给罗马人以致命打击,相反,为日后皮洛士的失败埋下了隐患。)线性回归总能绘制出一条直线,但如果它是一条无意义的直线,谁又会在乎呢?
所以我们现在看到了,仅仅因为可以进行一项优化,并不意味着达成了我们的目标。同时我们看到了,编造并可视化数据,是审视模型的假设的好方法。记住这一直觉,我们马上就会用到它。
假设不成立:非球形数据
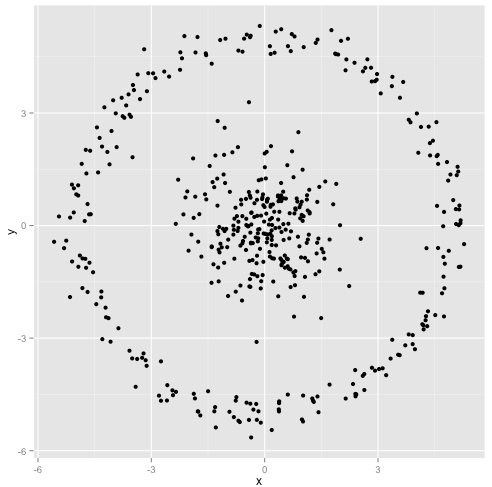
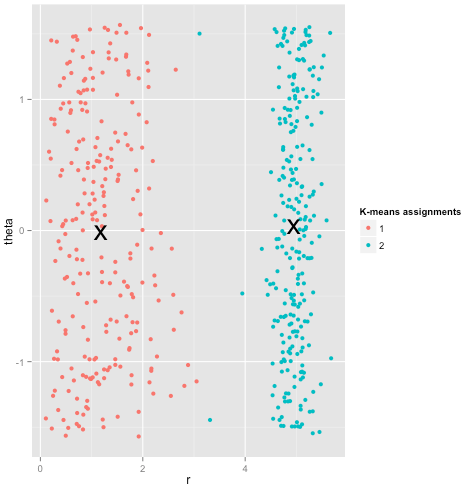
你主张K-均值算法在非球形聚类上工作良好。像这样的非球形数据?
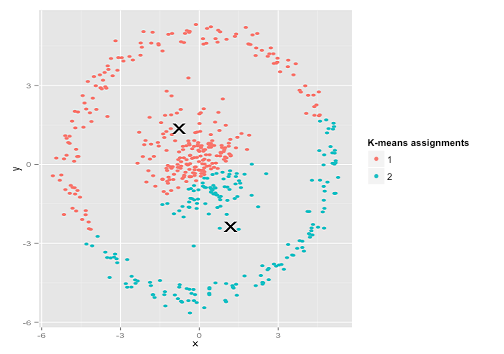
也许这不是你所期望的——但它是再合理不过的构建聚类方式。观察上图,我们人类能立刻识别出两个自然的数据点分组——不会有任何弄错的机会。现在,让我们看看K-均值表现如何:
这不对劲。K-均值试图将一头方形的猪塞进一个圆形的洞里——试图找到平滑的球形环绕的中心——它失败了。是的,它仍然最小化了聚类内的平方和——但和安斯库姆四重奏一样,这是皮洛士式胜利。
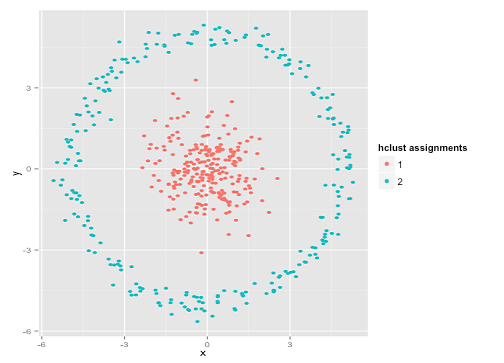
你也许会说“这不是一个公平的例子……没有聚类方法能找出这样奇葩的聚类”。并非如此!试下单链层次聚类:
搞定了!这是因为单链层次聚类对这一数据集的假设正确(有很多其他情况下,它会失败)。
你也许会说“这只是一个极端的、病态的个例”。但它并不是!例如,你可以将外围的群组从圆圈换成半圆,然后你会发现K-均值的表现仍然很糟糕(而单链层次聚类仍然表现良好)。我可以很容易地举出其他有问题的情况,而且这只是二维的情形。当你聚类16维数据时,会出现各种反常的情况。
最后,我想提醒一下,K-均值还是可以抢救一下的!如果你将数据转换为极坐标,聚类现在可以工作了:
这就是为什么理解方法背后的假设是必要的:它不仅告诉你方法的缺陷,还告诉你如何加以修正。
假设不成立:聚类尺寸不均匀
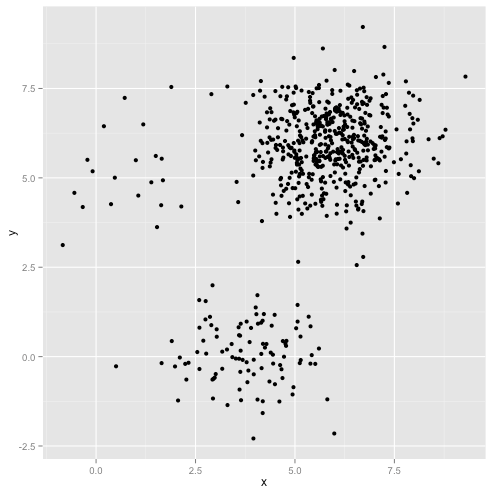
如果聚类的数据点数目分布不均匀会怎么样——这也会破坏K-均值聚类吗?好,假设聚类的尺寸分别为20、100、500。我依照多元高斯分布生成了聚类:
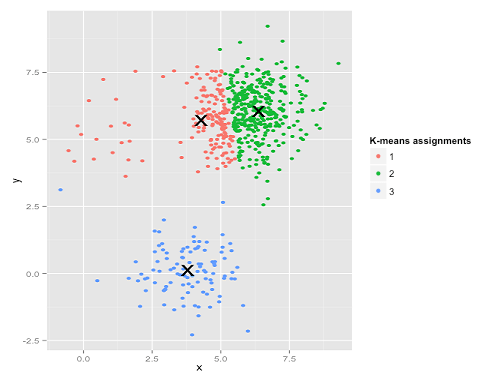
看起来K-均值大概能够找出这些聚类,不是吗?生成的每个群组都很平滑整齐。所以让我们试下K-均值:
哎哟。这次发生的事情有点微妙。当尝试最小化聚类内的平方和的时候,K-均值算法赋予了较大的聚类更多的“权重”。在实践中,这意味着K-聚类使小聚类远离其中心,中心被用来“分割”一个大得多的聚类。
探索一下这些例子(R代码在此),你可以构建更多K-均值错得离谱的情形。
结论:没有免费午餐
数学民俗中有一个迷人的解释,叫做“没有免费午餐定理”(Wolpert和Macready形式化了这一定理。这大概是我最喜欢的机器学习哲学定理,我很期待提起它的任何一个机会(先前我不是提过我很喜欢这个问题么?)。这一定理的基本想法(不严格的说法)是这样的:“平均了所有可能情形后,每个算法的表现一样好。”
听起来违背了直觉?考虑下,每个算法可以工作的情形,我都可以构建一个它错得离谱的情况。线性回归假定你的数据遵循一条直线——但如果它遵循的是一条正弦曲线会发生什么?t-测试假定每个样本来自正态分布:如果你丢进去一个离散值会发生什么?任何梯度上升算法可能陷入局部极大值,而任何监督分类可能被过拟合戏弄。
这意味着什么?这意味着假设是你力量的来源!Netflix给你推荐电影的时候,它会假设如果你喜欢一部电影,你会喜欢类似的电影(反之亦然)。想象在一个世界中,这个假设不成立,你的口味完全是随机的——随意地散布于不同的类型、演员和导演。他们的推荐算法就会错得离谱。这时候说“好吧,它仍然最小化某种期望平方误差,所以这个算法仍然可以工作”有意义吗?你不可能在对用户的口味不作一些假设的前提下构造推荐算法——正如你不可能在对聚类的性质不作一些假设的前提下构造聚类算法。
所以不要仅仅接受这些缺陷。了解它们,因此它们可以帮助你选择算法。理解它们,因此你可以调整你的算法,并转换你的数据以解决问题。热爱它们,因为如果你的模型永远不可能出错,那么它也将永远不可能成功。
原文地址:https://stats.stackexchange.com/questions/133656/how-to-understand-the-drawbacks-of-k-means/133694#133694