【策略精选】基于时间序列的协整关系的配对交易

本帖主要介绍了协整的基础知识,如何对两个时间序列进行协整关系检验,并实现了一个简单的配对交易策略。这里参考了百度百科和雪球文章《搬砖的理论基础:配对交易 Pair Trading》。
1协整关系的逻辑
统计套利之配对交易是一种基于数学分析交易策略,其盈利模式是通过两只证券的差价(spread)来获取,两者的股价走势虽然在中途会有所偏离,但是最终都会趋于一致。配对交易就是利用这种价格偏离获取收益。具有这种关系的两个股票,在统计上称作协整性(cointegration),即它们之间的差价会围绕某一个均值来回摆动,这是配对交易策略可以盈利的基础。通俗点来讲,如果两个股票或者变量之间具有强协整性,那么不论它们中途怎么走的,它们的目的地总是一样的。
2协整关系的发展
经典回归模型是建立在平稳数据变量的基础之上的,对于非平稳变量,不能使用经典回归模型,否则会出现虚假回归等诸多问题,但是实际应用中大多数时间序列是非平稳的,1987年Engle和Granger提出的协整理论及其方法,为非平稳序列的建模提供了另一种途径。虽然一些经济变量的本身是非平稳序列,但是,它们的线性组合却有可能是平稳序列。这种平稳的线性组合被称为协整方程,且可解释为变量之间的长期稳定的均衡关系。
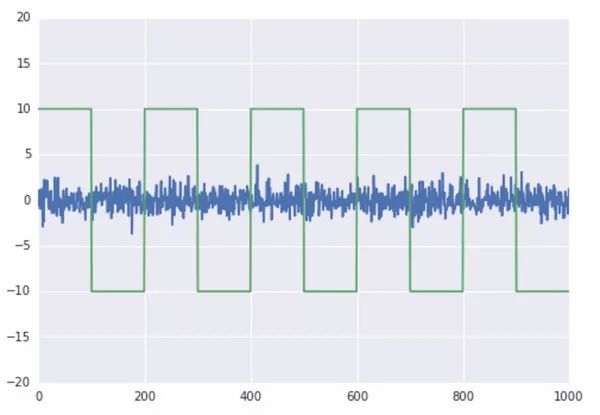
需要特别注意的是协整性和相关性虽然比较像,但实际是不同的两个东西。两个变量之间可以相关性强,协整性却很弱,比如说两条直线,y=x和y=2x,它们之间的相关性是1,但是协整性却比较差;方波信号和白噪声信号,它们之间相关性很弱,但是却有强协整性。
(完整版请点击文末“阅读原文”获取)
3协整关系的运用
这里还有介绍一个关于时间序列的基本概念:平稳性。平稳分为两种:强(严)平稳:给定随机过程X(t),t属于T,其有限维分布组为F(x1,x2,...xn;t1,t2,...,tn),t1,t2,...,tn属于T,对任意n任意的t1,t2,...,tn属于T,任意满足t1+h,t2+h,...,tn+h属于T的h,总有F(x1,x2,...xn;t1,t2,...,tn)=F(x1,x2,...xn;t1+h,t2+h,...,tn+h);宽(弱)平稳:给定二阶矩过程(二阶矩存在)X(t),t属于T,如果X(t)的均值函数u(t)是常数,相关函数R(t1,t2)=f(t2-t1)即相关函数只与时间间隔有关。我们通常用的都是弱平稳。
单整阶数:当原序列是非平稳的,需要对序列进行差分(后一项减前一项),直到为平稳序列,差分几次就是几阶。
协整关系存在的条件是:只有当两个变量的时间序列{x}和{y}是同阶单整序列即I(d)时,才可能存在协整关系(这一点对多变量协整并不适用)。因此在进行y和x两个变量协整关系检验之前,先用ADF单位根检验对两时间序列{x}和{y}进行平稳性检验。平稳性的常用检验方法是图示法与单位根检验法。
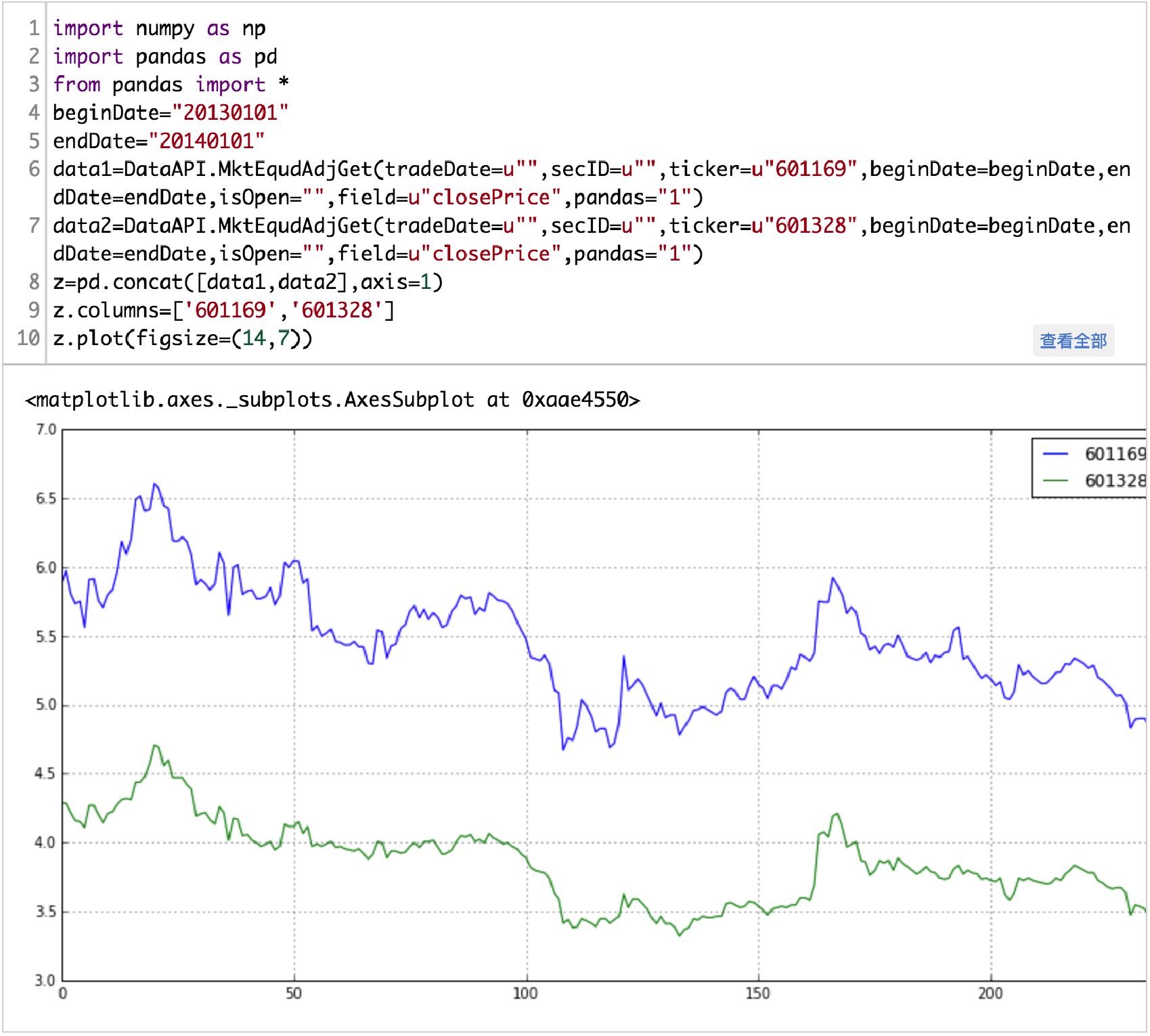
下面举个栗子,我取了601169北京银行 ,601328交通银行两只股票,看它们在2013年一年的时间序列是否存在协整性。
(完整版请点击文末“阅读原文”获取)
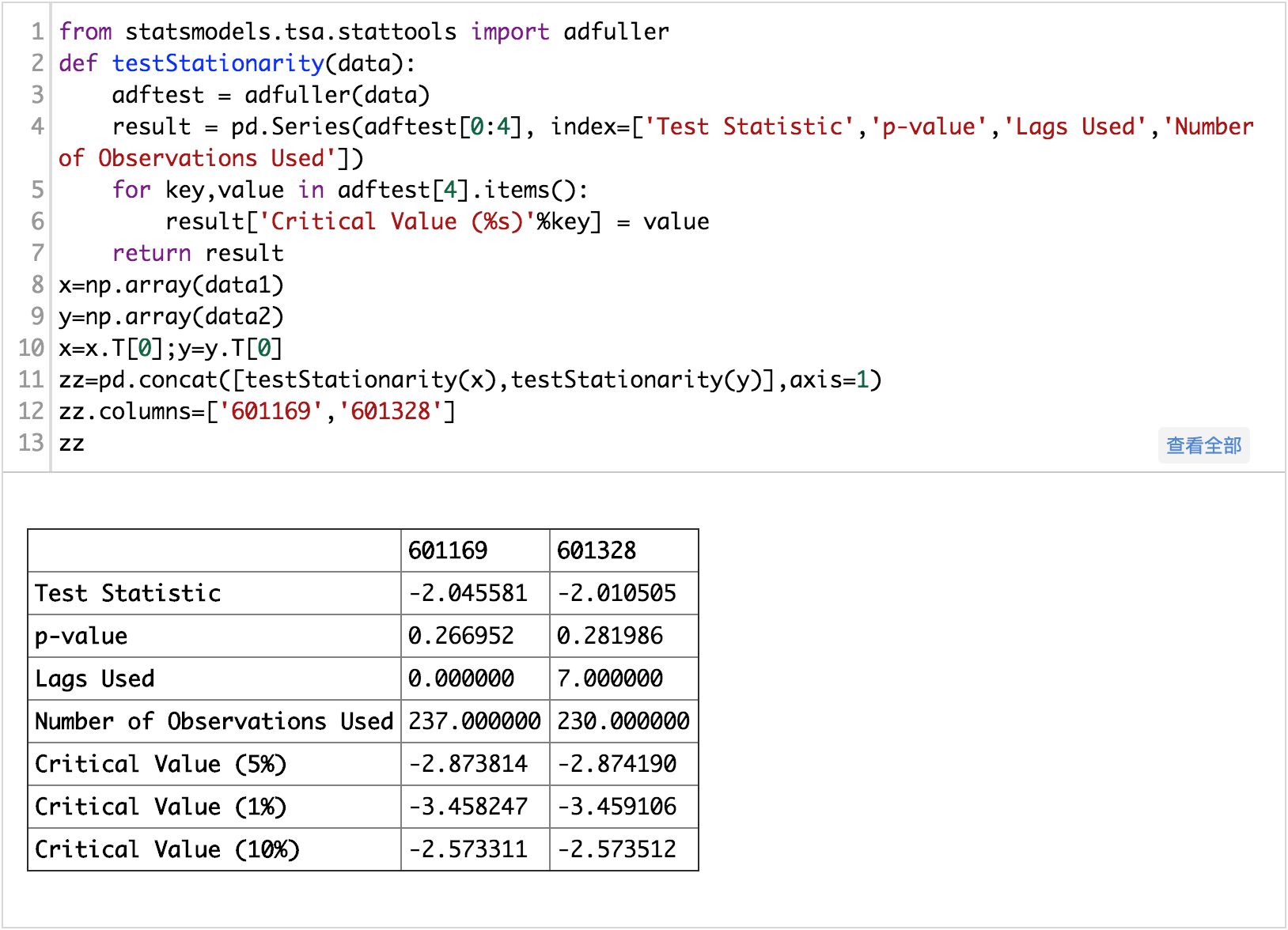
先定单整阶数,即检验平稳性,作差分,直到序列平稳。这里检验平稳性用的是ADF单位根检验法,原假设为序列具有单位根,即非平稳,对于一个平稳的时序数据,就需要在给定的置信水平上显著,拒绝原假设。也就是说Pvalue很低时,序列平稳。
(完整版请点击文末“阅读原文”获取)
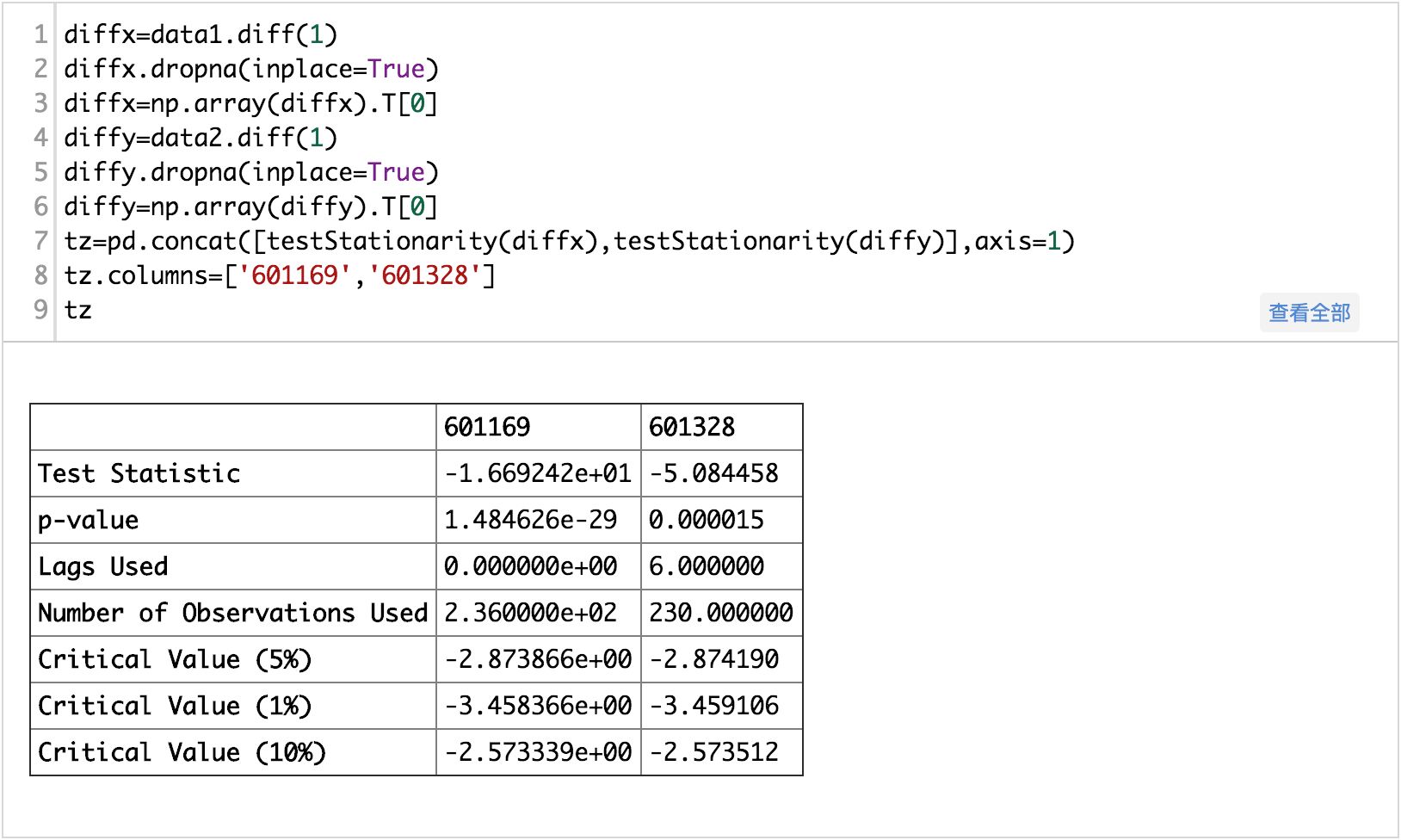
可以看出两只股票的P值都还高,不能拒绝原假设,即数据非平稳,下面做一阶差分以后,再检验平稳性:
(完整版请点击文末“阅读原文”获取)
一阶差分以后,两个序列就已经平稳了,他们的单整阶数都是一,所以是单整同阶的,下面就可以做协整了:这里的原假设是两者不存在协整关系。
(完整版请点击文末“阅读原文”获取)
p值低于临界值,所以拒绝原假设,两者存在协整关系。
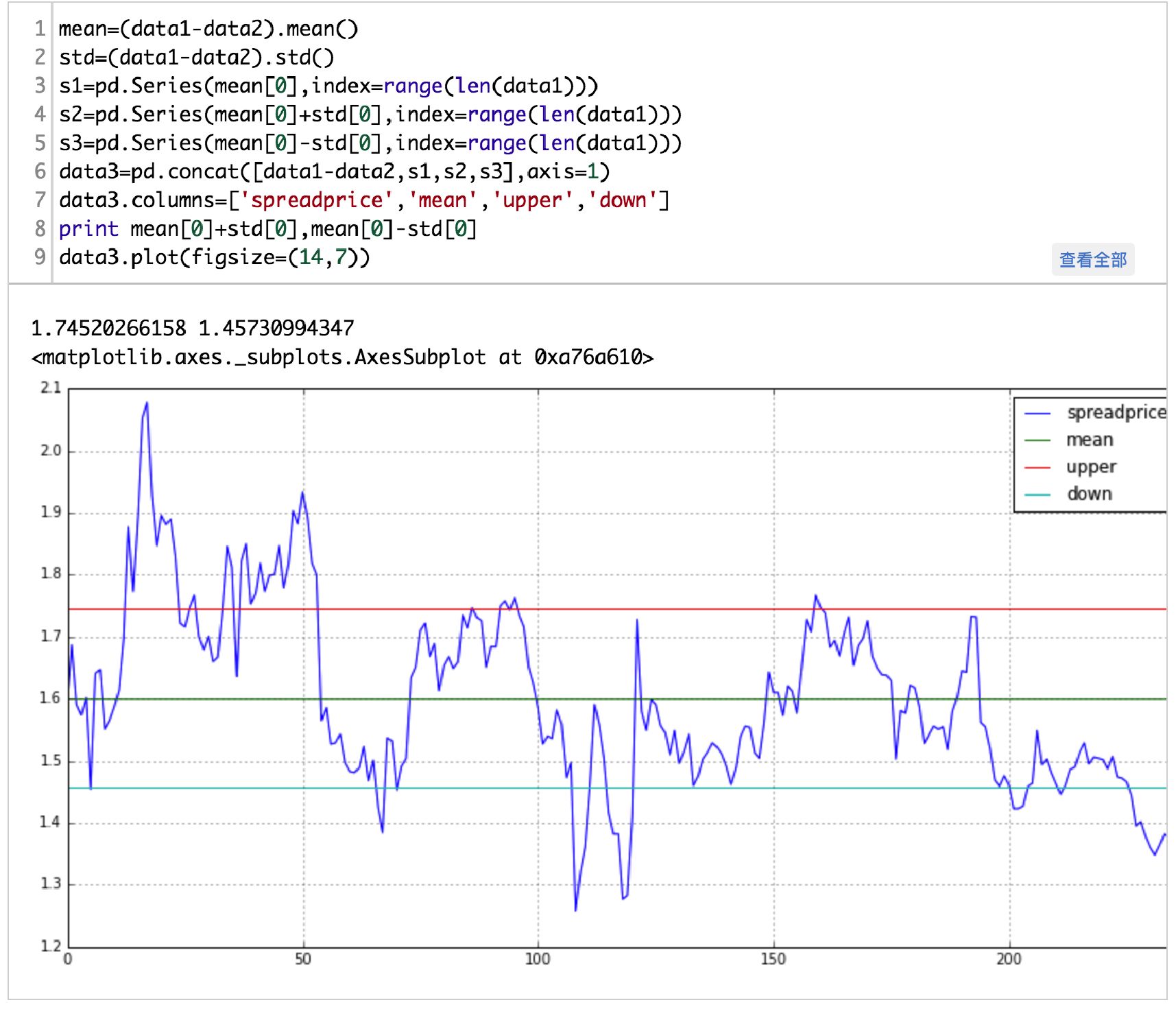
接下来就可以根据两者的协整关系做配对交易了。先画出两者的差价序列:
(完整版请点击文末“阅读原文”获取)
这样,如果可以卖空的话,一个最简单的配对交易如下:
spreadprice大于1.7452时,卖空差价,即卖空601169北京银行,买入601328交通银行。
spreadprice小于1.4573时,买入差价,即买入601169北京银行,卖空601328交通银行。
spreadprice靠近零时,平仓。
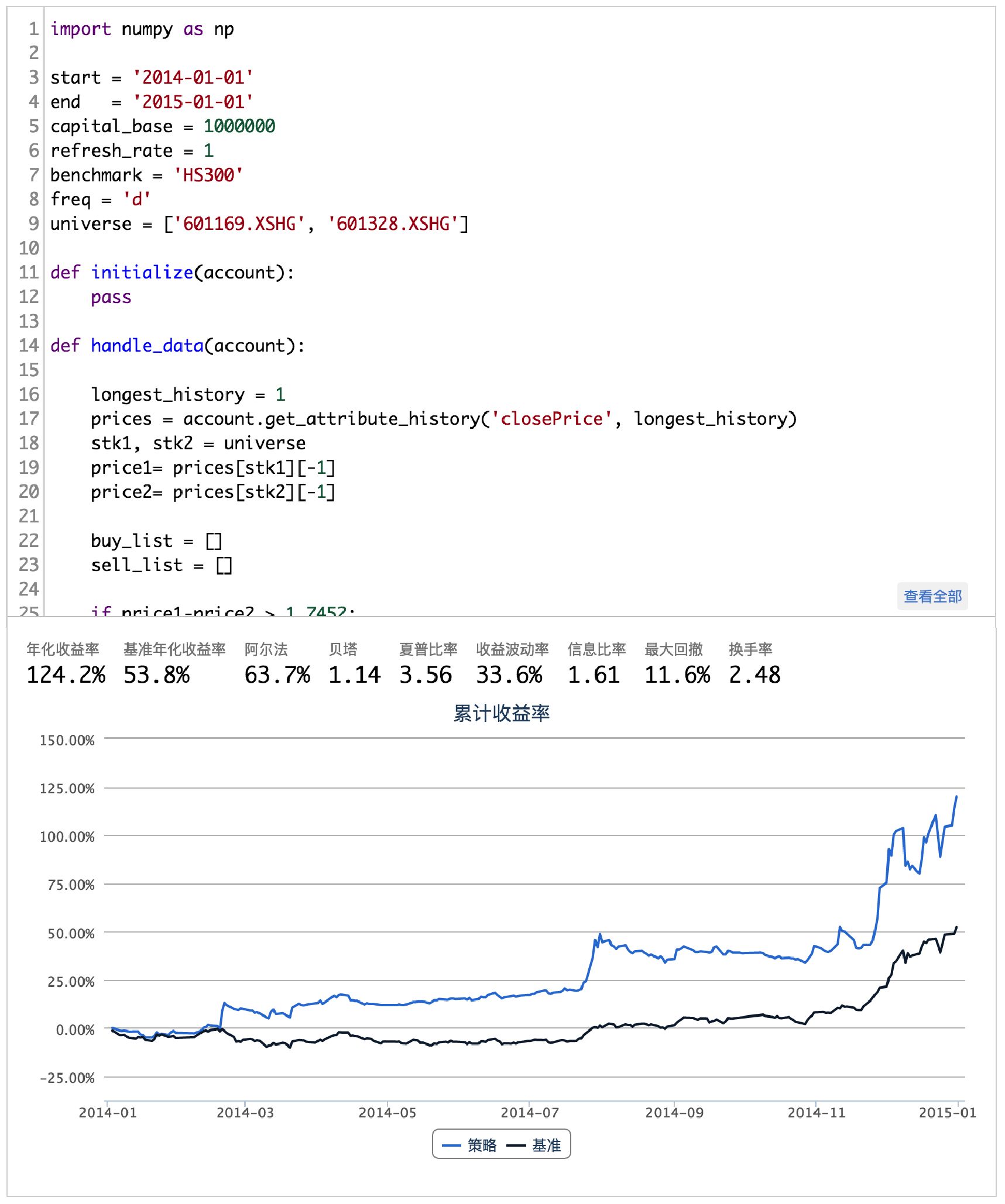
A股市场无法卖空个股,对于无法卖空个股的A股市场,上述配对交易策略中的卖空改为卖出即可。下面我们来实现上述策略,看看这两支股票的配对交易在2014年里的表现:
(完整版请点击文末“阅读原文”获取)
4总结
上述过程重在描述理论,以供大家研究。此外,这种统计套利的方式在期货市场也会有其用武之地。
量化之路漫漫其修远兮,吾将上下而求索。
--- the end ---
Read More:
优矿是由通联数据出品,覆盖研究、回测、模拟、实盘交易全流程的量化平台。优矿不仅拥有通联海量的金融数据、动态丰富的策略框架,同时还通过知识库信号库提供持续的知识输出,满足用户在研究过程中高效获取、迅速验证、多维度挖掘、多策略并行的迫切需求,为投资决策提供重要支持。
扫二维码,立即预约试用!
↓↓↓ 点击"阅读原文" 【查看源码】