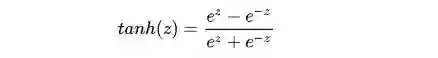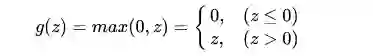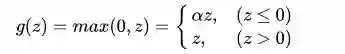【吴恩达deeplearning.ai笔记二】通俗讲解神经网络下

                                                                                                                                                                             

点击上方 “机器学习研究会”可以订阅

摘要

 

转自：机器学习算法与自然语言处理

本文是吴恩达老师DeepLearning.ai课程笔记，神经网络下篇内容，上篇见【吴恩达deeplearning.ai笔记二】通俗讲解神经网络上

4激活函数

建立一个神经网络时，需要关心的一个问题是，在每个不同的独立层中应当采用哪种激活函数。逻辑回归中，一直采用sigmoid函数作为激活函数，此外还有一些更好的选择。

tanh函数（Hyperbolic Tangent Function，双曲正切函数）的表达式为：

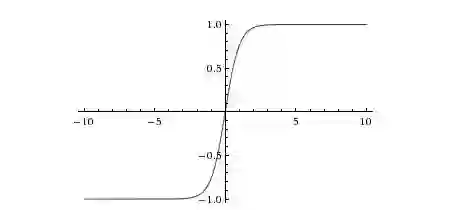
函数图像为：

tanh函数其实是sigmoid函数的移位版本。对于隐藏单元，选用tanh函数作为激活函数的话，效果总比sigmoid函数好，因为tanh函数的值在  到  之间，最后输出的结果的平均值更趋近于  ，而不是采用sigmoid函数时的  ，这实际上可以使得下一层的学习变得更加轻松。对于二分类问题，为确保输出在  到  之间，将仍然采用sigmiod函数作为输出的激活函数。

然而sigmoid函数和tanh函数都具有的缺点之一是，在  接近无穷大或无穷小时，这两个函数的导数也就是梯度变得非常小，此时梯度下降的速度也会变得非常慢。

线性修正单元，也就是上面举例解释什么是神经网络时用到的ReLU函数也是机器学习中常用到的激活函数之一，它的表达式为：  

函数图像为：

当 z大于0时，ReLU函数的导数一直为1 ，所以采用ReLU函数作为激活函数时，随机梯度下降的收敛速度会比sigmoid及tanh快得多，但负数轴的数据都丢失了。

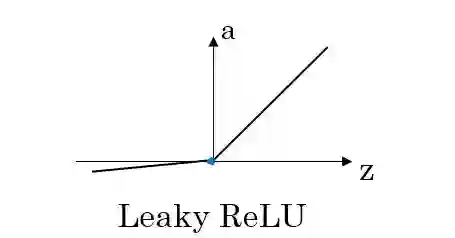
ReLU函数的修正版本，称为Leaky-ReLU，其表达式为：  

函数图像为：

其中alpha是一个很小的常数，用来保留一部非负数轴的值。

可以发现，以上所述的几种激活函数都是非线性的，原因在于使用线性的激活函数时，输出结果将是输入的线性组合，这样的话使用神经网络与直接使用线性模型的效果相当.

此时神经网络就类似于一个简单的逻辑回归模型，失去了其本身的优势和价值。

原文链接：

https://mp.weixin.qq.com/s/Hlvs8wYZ2tPjmSroK5Gi9g

“完整内容”请点击【阅读原文】

↓↓↓