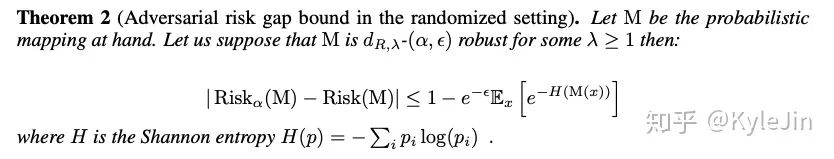模型的Robustness和Generalization是什么关系？

嘿，记得给“机器学习与推荐算法”添加星标

---

来自 | 知乎 

链接 | https://www.zhihu.com/question/410332622/

编辑 | 机器学习与推荐算法

最近在看一些利用对抗学习技术提升模型鲁棒性以及泛化能力的文章，然后看到了知乎有相关的讨论，特此整理一下供大家学习交流。

模型的Robustness和Generalization是什么关系？

Robustness是模型对input perturbation的变化程度；统计学习中的Generalization是模型对来自与训练集同分布数据的预测能力；近期还有OoD generalization的概念，考虑的是对与训练数据分布有差别的数据的泛化能力。它们之间有关系吗？有什么关系？

---

知乎作者：KyleJin

https://www.zhihu.com/people/mai-kang-ming

最近在研究这个问题，抛砖引玉。

经验上来说，毫无疑问他们两者是存在联系的。体现的比较明显的领域在于弱监督学习（例如，半监督学习），会使用各种各样的数据增强（例如，加入噪声，反转，裁切，甚至对抗等），让模型变得对输入的细微扰动不敏感，从而减少过拟合（因为在标注数据少的情况下，过拟合是容易发生的），提升泛化性能。类似的工作比如

• Tarvainen and Valpola 2017: Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results

• Miyato et al. 2019: Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning

但是，把鲁棒性做的极端一点，即使是大幅度的扰动，也无法改变模型的输出，那么模型就会变成过平滑/随机模型，从而降低预测性能。

理论上，我所了解到的，有如下理论的相关结果

1. Robustness may be at odds with accuracy. 

https://arxiv.org/pdf/1805.12152.pdf

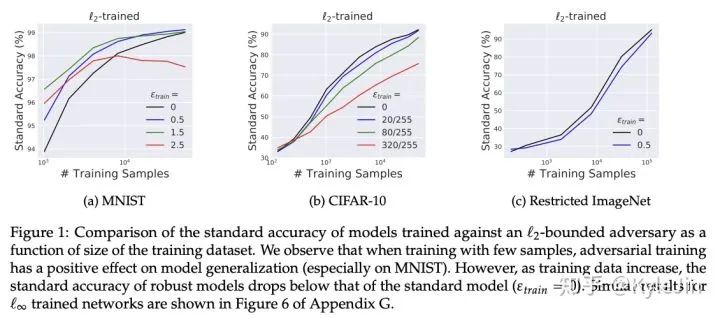
这篇文章的结果是这么说的：

首先，经验上来说，在训练数据不足的时候，加入robustness（例如，对抗样本训练）会对模型的泛化起到积极的作用。但是，当数据量变大/变得复杂，这个效果就消失了（哪怕是在稍微复杂一丢丢的数据集，例如CIFAR10，CIFAR100上，这个效果就从未体现出来）。这是好理解的，在简单/小数据上，过拟合/欠鲁棒发生了，但是程度可能非常有限。

随后作者从理论上用一个简单的仿真数据解释了这个问题，数据集构造如下：

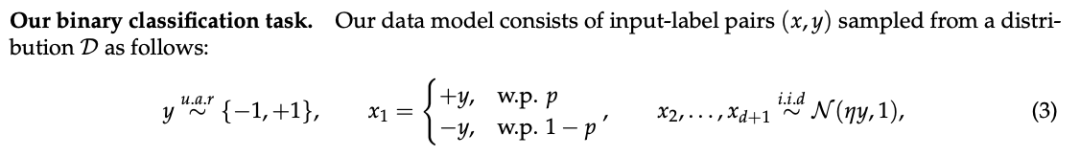
作者在这个简单的数据集下证明了robustness和accuracy是存在矛盾的，很符合我们通过实验观测的结果。

2. Theoretical evidence for adversarial robustness through randomization. 

https://papers.nips.cc/paper/9356-theoretical-evidence-for-adversarial-robustness-through-randomization.pdf

本文中作者证明了，如果想通过随机化的方式增强鲁棒性，那么必然面对精确度的损失（作者用预测的期望熵来衡量）

符号很复杂，不过表达的意思就是，如果加入较大的噪声让模型变鲁棒，那么H(M(x))，即模型输出的熵一定变大。当然，本文作者只探讨了“随机化”一种方式对robustness-generalization关系的影响。

---

我个人的理解，鲁棒性和泛化是一个权衡的关系，权衡体现在上面说的，过鲁棒-无法泛化，欠鲁棒也无法泛化。这个权衡，我们可以分两方面看。

在现实中，一般模型是都欠鲁棒的，一个间接的证据就是很多看起来很离奇的正则化都可以让模型test accuracy变高，例如mixup(Zhang et al. 2018), StochasticDepth(Huang et al. 2016), Shake-shake (Gestaldi et al. 2017)等等，所以在实际应用中鲁棒性应该是越强越好。

在权衡的另一端，鲁棒性的一个很强的例子是对对抗样本鲁棒（adversarial robustness），是一个非常强的约束，从而会导致test accuracy大幅下降。这体现了过鲁棒-无法泛化，在刚才提到的paper里也有论证这一点。

一些粗浅的见解先写到这里，下班了，明天再写

---

知乎作者：心似风往

https://www.zhihu.com/people/king-lee-97-56

很喜欢这个问题，尽管没人邀请，还是放下手中阅读到一半的论文，来聊聊这个问题。毕竟知乎那么多人，提出那么多问题，收到那么多人回答问题的邀请，但是喜欢的问题真的百里挑一。

Part 1 关于 robustness 和 accuracy 的问题

正如 @KyleJin 所回答的：

Robustness 和 accuracy 确实有很强的tradeoff，这不仅在他举的robustness may be at odds with accuracy^[1]文章中有所体现，如果你有关注这个研究点，你会发现有不少文章都在研究这个问题，比如

1. Theoretically principled trade-off between robustness and accuracy ^[2]

这篇文章中，作者将 prediction error for adversarial example(robust error)拆分成 natural(classification) error 和 boundary error的和， 并且据此证明了upper bound。根据他们的分析，提出了一个 trade adversarial robustness off against accuracy 的defense method。是一个非常值得一读的 paper。

这篇 paper 让我想起了之前读的一篇也非常有意思的文章，名字叫 adversarial examples are not bugs， they are features^[3]。这篇文章也同样采用了拆分的方法，将 accuracy 拆分成 standard accuracy 和 adversarial accuracy，并根据实验分析得出  adversarial examples are not bugs， they are features的结论。想法很巧妙，实验也很简单，但是解释了一个非常重要的问题，也很值得一读。

2. Understanding and Mitigating the tradeoff between robustness and accuracy ^[4]

正常情况下，经过 adversarial training 的模型比正常训练得出的模型更robust，但是这个 robustness是通过牺牲 accuracy得到的,所以 standard  training  和adversarial training得到的accuracy是有gap的。但是他们发现在CIFAR-10的实验中， the gap between the standard error of adversarial training and standard training decreases as we increase the labeled data size, thereby also suggesting the tradeoff could disappear with infinite data。所以他们在infinite data的情况下分析tradeoff。

他们得出的结论是: we show that the standard error could increase even when the augmented perturbations have noiseless observations from the optimal linear predictor. We then prove that the recently proposed robust self-training (RST) estimator improves robust error without sacrificing standard error for noiseless linear regression.

3. A closer look at accuracy vs. robustness^[5]

这篇文章我还没仔细看，是我这两天刚发现的，贴一下他们的结论，等仔细读完了再来补。

We argue that the gap between theory and practice arises from two limitations of current methods: either they fail to impose local Lipschitzness or they are insufficiently generalized. We explore combining dropout with robust training methods and obtain better generalization. We conclude that achieving robustness and accuracy in practice may require using methods that impose local Lipschitzness and augmenting them with deep learning generalization techniques.

4. 如果有其他新的发现再来补。

---

Part 2  直接提到有关robustness 和 generalization的问题文章

1. Adversarial Training Can Hurt Generalization ^[6]

adversarial training 的目标就是提高 robustness，那这篇文章标题直接说 adversarial training 损害了generalization，其实也就是在说 tradeoff的事情。

2. Adversarially Robust Generalization Requires More Data ^[7]

作者也是在实验中发现了gap的问题，提出如果你想要你的adversarial robustness generalize 的更好，来吧，去搜集更多的data。

3. Stability and generalization^[8]

其实我个人觉得 stability 和 robustness是有关系的，或者说某种意义上就是同一个东西，所以这篇文章也可以看看。

这是我很久以前读的文章了，具体我都忘了，等我回头再读之后再来更清楚的回答，这里贴一下我的notes：

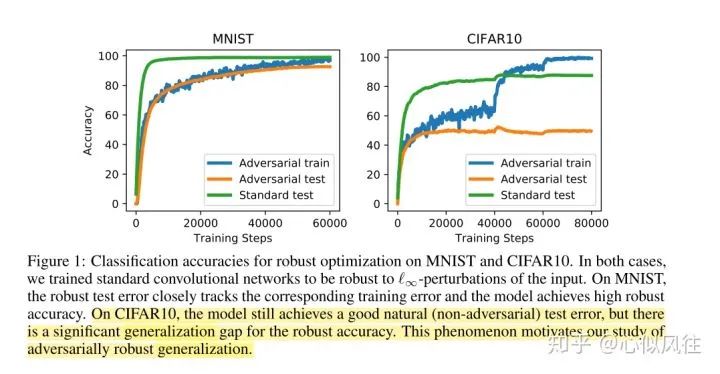
1.Defining the Stability of a Learning Algorithm
2.Generalization Bounds for Stable Learning Algorithms：
the empirical error and the leave-one-out error differ from the true error in a similar way.
3.Stable Learning Algorithms: discussion6
For regularization algorithms, we obtained bounds on the uniform stability of the order of β =O( 1/λm).
4.we obtained bounds on the generalization error of the following typeR ≤ Remp +O ( 1/λ √m)
总结：Our main result is an exponential bound for algorithms that have good uniform stability. We then proved that regularization algorithms have such a property and that their stability is controlled by the regularization parameter λ. This allowed us to obtained bounds on the generalization error of Support Vector Machines both in the classification and in the regression framework that do not depend on the implicit VC-dimension but rather depend explicitly on the tradeoff parameter C.

4. 有新的有意思的文章再更新。

参考：

^Robustness may be at odds with accuracy https://arxiv.org/pdf/1805.12152.pdf

^theoretically principled trade-off between robustness and accuracy https://arxiv.org/pdf/1901.08573.pdf

^adversarial examples-are-not-bugs， they are features https://papers.nips.cc/paper/8307-adversarial-examples-are-not-bugs-they-are-features.pdf

^Understanding and Mitigating the tradeoff between robustness and accuracy https://arxiv.org/pdf/2002.10716.pdf

^A Closer Look at Accuracy vs. Robustness https://arxiv.org/pdf/2003.02460.pdf

^Adversarial Training Can Hurt Generalization https://arxiv.org/pdf/1906.06032.pdf

^Adversarially Robust Generalization Requires More Data http://papers.nips.cc/paper/7749-adversarially-robust-generalization-requires-more-data.pdf

^Stability and generalization http://www.jmlr.org/papers/volume2/bousquet02a/bousquet02a.pdf

推荐阅读

推荐系统实用分析技巧

基于GNN和哈希学习的高效推荐系统

KDD2020最佳论文: 关于个性化排序任务评价指标的大讨论

喜欢的话点个在看吧👇