算法系列 图数据结构探索(无向图搜索)
算法是基础,小蓝同学准备些总结一系列算法分享给大家,这是第10篇《无向图搜索》,非常赞!希望对大家有帮助,大家会喜欢!
前面系列文章:
随着图数据库,图计算,知识图谱的兴起,图这种数据结构使用逐渐面向大众,更为的广泛。使用我们这个篇章会给大家介绍图的一些数据结构及其对应相关的一些算法,希望大家能够喜欢,并对大家理解知识图谱,图计算有所帮助
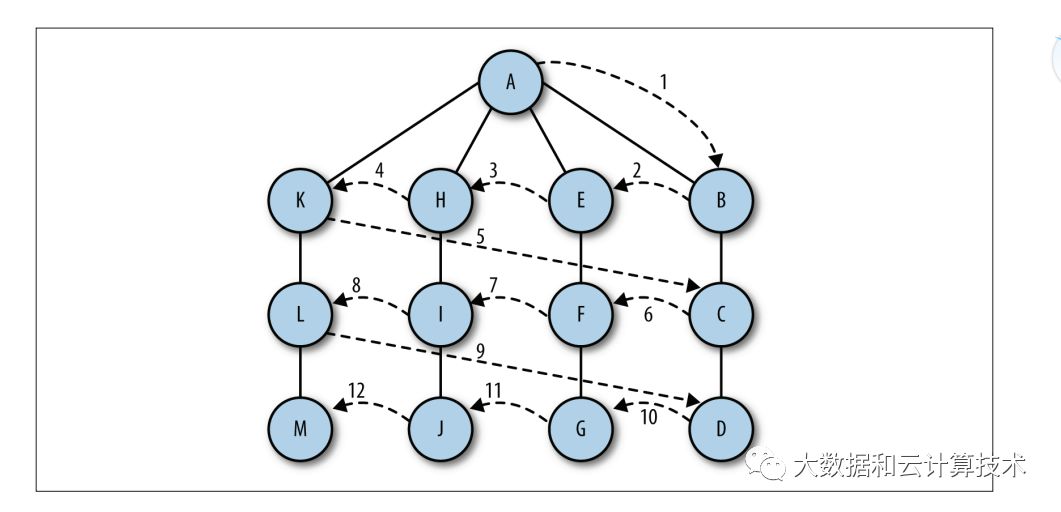
本篇从无向图搜索讲起,说起无向图搜索 主要分为两块一块时深度优先,一块时广度优先。其实图搜索可以我在电脑里有一个文件夹,这个文件夹里有很多细分文件夹,而我们要便利每一个文件夹的一个过程。
而深度优先指的是,我先打开最开始的那个文件夹,之后再打开他下面的第一个文件夹,之后再打开这个子文件的子文件夹,循环往复的一个过程 ,直到所有的文件夹里的文件都便利过一遍。同理广度优先是指我先打开这个文件夹里的所有文件,然后再逐个打开他子文件的所有文件的一个循环往复的一个过程。
二话不说上代码吧 哈哈
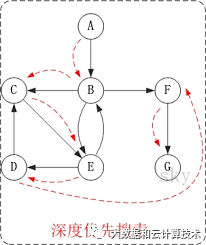
深度优先搜索代码
public class DepthFirstPaths {
private boolean[] marked;
private int[] edgeTo;
private final int s;
public DepthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
dfs(G, s);
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
dfs(G, w);
}
}
}
public boolean hasPathTo(int v) {
return marked[v];
}
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) {
return null;
}
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x]) {
path.push(x);
}
path.push(s);
return path;
}
public static void main(String[] args) {
Graph G = new Graph(new In(args[0]));
int s = Integer.parseInt(args[1]);
DepthFirstPaths search = new DepthFirstPaths(G, s);
for (int v = 0; v < G.V(); v++) {
StdOut.print(s + " to " + v + ": ");
if (search.hasPathTo(v)) {
for (int x : search.pathTo(v)) {
if (x == s) {
StdOut.print(x);
} else {
StdOut.print("-" + x);
}
}
}
StdOut.println();
}
}
广度优先搜索代码
public class BreadthFirstPaths {
private boolean[] marked;
private int[] edgeTo;
private int[] distTo; // Add for Exercise 4.1.13
private final int s;
public BreadthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
distTo = new int[G.V()]; // Add for Exercise 4.1.13
this.s = s;
bfs(G, s);
}
private void bfs(Graph G, int s) {
Queue<Integer> queue = new Queue<Integer>();
marked[s] = true;
// Add for Exercise 4.1.13
for (int v = 0; v < G.V(); v++) {
distTo[v] = Integer.MAX_VALUE;
}
distTo[s] = 0;
queue.enqueue(s);
while (!queue.isEmpty()) {
int v = queue.dequeue();
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
marked[w] = true;
distTo[w] = distTo[v] + 1; // Add for Exercise 4.1.13
queue.enqueue(w);
}
}
}
}
public boolean hasPathTo(int v) {
return marked[v];
}
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) {
return null;
}
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x]) {
path.push(x);
}
path.push(s);
return path;
}
/**
* Exercise 4.1.13
*
* @param v
* @return
*/
public int distTo(int v) {
return distTo[v];
}
public static void main(String[] args) {
Graph G = new Graph(new In(args[0]));
int s = Integer.parseInt(args[1]);
BreadthFirstPaths search = new BreadthFirstPaths(G, s);
for (int v = 0; v < G.V(); v++) {
StdOut.print(s + " to " + v + ": ");
if (search.hasPathTo(v)) {
for (int x : search.pathTo(v)) {
if (x == s) {
StdOut.print(x);
} else {
StdOut.print("-" + x);
}
}
}
StdOut.println();
}
}
}
应用再知识图谱中风控大量的应用了无向图搜索的内容,有兴趣的同学可以自己去找找相关资料。
猜你喜欢
大数据和云计算技术周报(第56期)
加入技术讨论群
《大数据和云计算技术》社区群人数已经3000+,欢迎大家加下面助手微信,拉大家进群,自由交流。
喜欢QQ群的,可以扫描下面二维码:
欢迎大家通过二维码打赏支持技术社区(英雄请留名,社区感谢您,打赏次数超过108+):
登录查看更多
相关内容
Arxiv
10+阅读 · 2018年1月29日
Arxiv
9+阅读 · 2018年1月27日