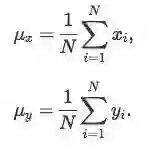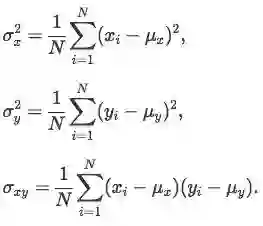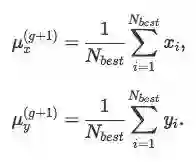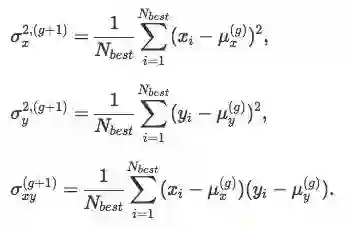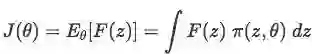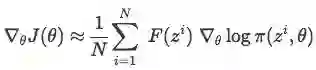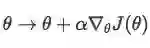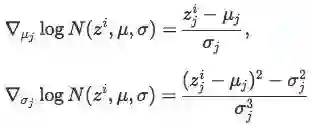ML领域的生物进化论，进化策略图文详解

论智

编译 | Bot

来源 | Otoro

编者按：进化策略是德国的I. Rechenberg和HP. Schwefel于1963年提出的参数优化方法，它模仿生物进化原理，不论参数发生何种变化，它的特征总遵循零均值、某一方差的高斯分布。日前，机器学习爱好者大トロ在博客中图文并茂地对进化策略进行了详解，并授权论智把成果分享给中国读者。

介绍

神经网络模型具有高度的表达性和灵活性，如果我们能找到一组合适的模型参数，它能帮助我们解决许多具有挑战性的的问题。近年来，深度学习的成功主要来源于它能利用反向传播算法高效计算每个模型参数上目标函数的梯度。通过这些梯度，我们能更高效地搜索参数空间，从中找出最合适的解。

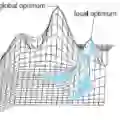
然而，反向传播算法也有诸多局限，如在强化学习（RL）问题中，我们可以训练一个神经网络来对下一步动作执行做出决策，以实现最终目标。但我们无法判断沿着当前agent梯度发展，模型在下一阶段是否能获得奖励信号，尤其是在时间步长较长的情况下。换个角度说，即使最后算出了精确的梯度，那也可能只是局部最优值或局部极小值。

反向传播算法陷入局部最优值

信用分配问题（ credit assignment problem），即在建立模型前，你需要知道哪些动作会触发奖励信号及它们的奖励贡献大小。它至今仍是RL一大关键挑战，虽然近年来取得了巨大进展，但在奖励信号稀疏时，信用分配依然十分棘手。现实世界中的奖励可能是稀疏的、嘈杂的，有时甚至只有一次奖励，如年底公司发的年终奖，你可能永远没法知道它为什么那么低，因为那是由你的老板决定的。对于这类问题，我们不能把结果依赖于在嘈杂数据中进行无意义的梯度计算，一种更合适的解决方法是使用黑盒优化技术，如遗传算法（GA）和进化策略（ES）。

今年3月，OpenAI曾发表了一篇名为Evolution Strategies as a Scalable Alternative to Reinforcement Learning（进化策略：可代替强化学习）的文章，指出进化策略只需少量计算就能在效率上比肩标准的强化学习，同时还能克服后者的诸多不便。放弃梯度计算意味着进化策略能进行更有效的评估，可以把任务分配给上千台计算机并行计算。根据实验，他们得出的一大推论是：和强化学习相比，进化策略产生的结果往往更加多样化。

什么是进化策略

二维Rastrigin函数有许多局部最优

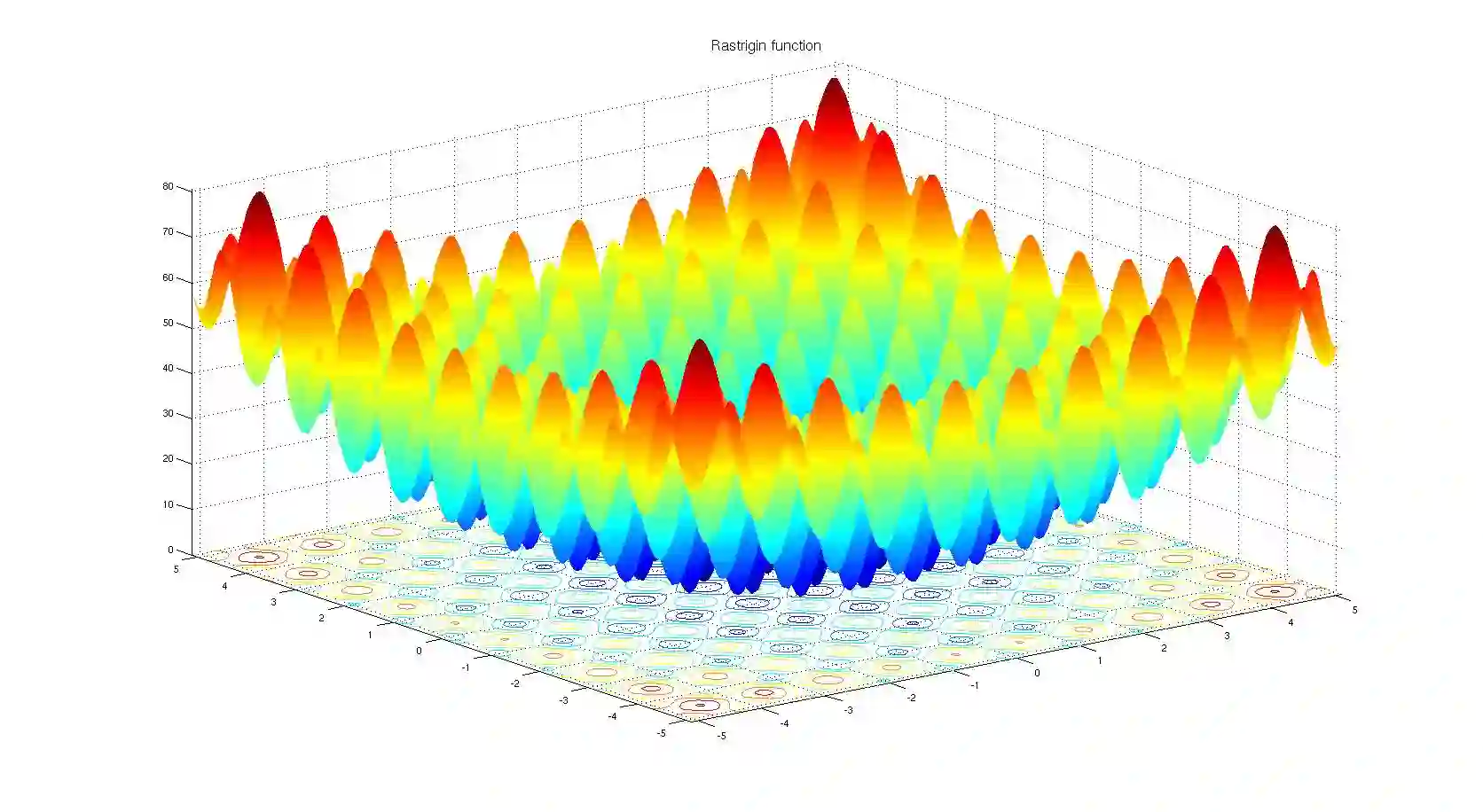
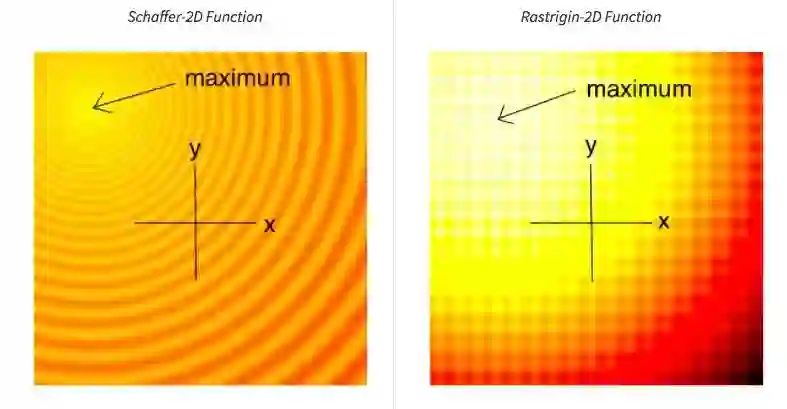
下面两幅图代表用于测试黑盒优化技术的两个玩具问题 ，前者是Schaffer函数图，后者是Rastrigin函数图，图中的浅色区域代表空间高值F(x,y)。正如你所看到的，图中有许多局部最优值，因此我们的任务是找到一组模型参数(x, y)，使得F(x,y)无限接近空间极大值。

尽管进化策略已经有很多官方定义，但在本文中，我们暂且把它简单解释为一种为用户提供一组候选解来评估问题的方法。算法评估基于一个目标函数，它采用给定的候选解，并返回一个单一的适应值。基于当前解的适应值，算法会产生下一代候选解，而下一代的适应值结果比上代更佳。如此循环往复，直到用户得到了满意的解，整个迭代过程才会终止。

如果想创建一个名为EvolutionStrategy的进化策略算法，你可以这么写：

solver = EvolutionStrategy()
while True:
  # ask the ES to give us a set of candidate solutions
  solutions = solver.ask()
  # create an array to hold the fitness results.
  fitness_list = np.zeros(solver.popsize)
  # evaluate the fitness for each given solution.
  for i in range(solver.popsize):
    fitness_list[i] = evaluate(solutions[i])
  # give list of fitness results back to ES
  solver.tell(fitness_list)
  # get best parameter, fitness from ES
  best_solution, best_fitness = solver.result()
  if best_fitness > MY_REQUIRED_FITNESS:
    break

虽然每一代种群规模是不变的，但其实它也没必要变化，因为进化策略可以根据需要生成尽可能多的候选解，并从每一代更新参数的分布中采样。以下是一个简单的例子。

进化策略简单示例

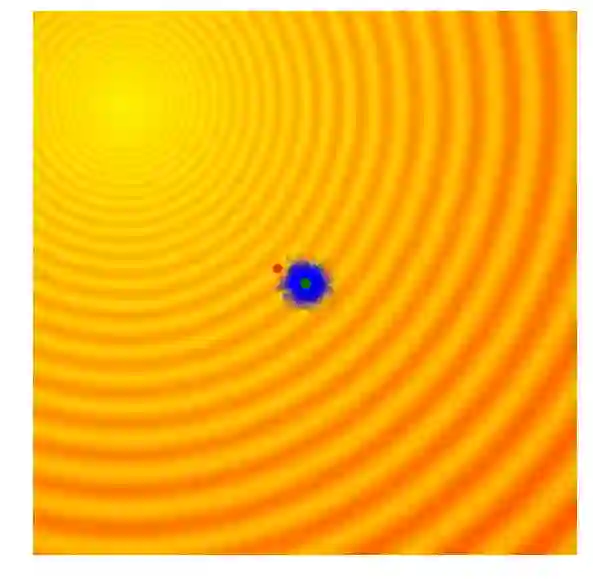
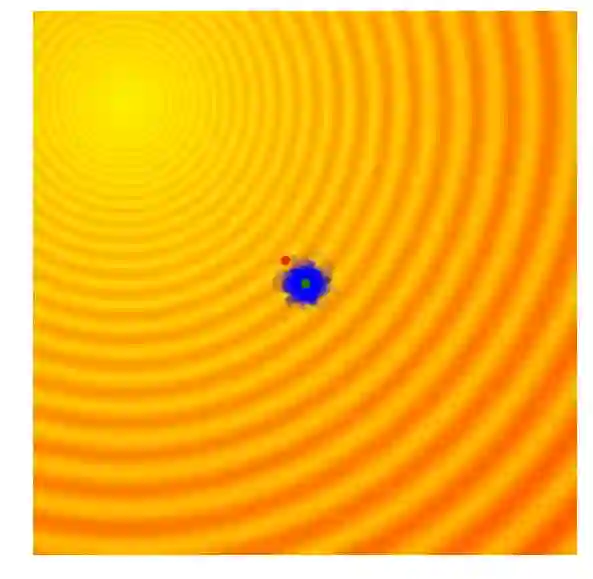
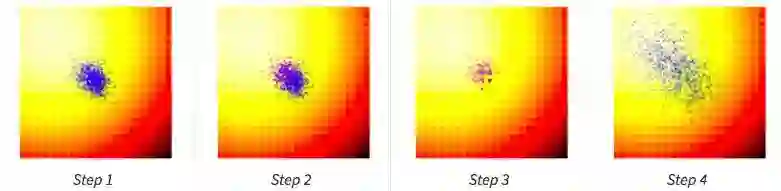
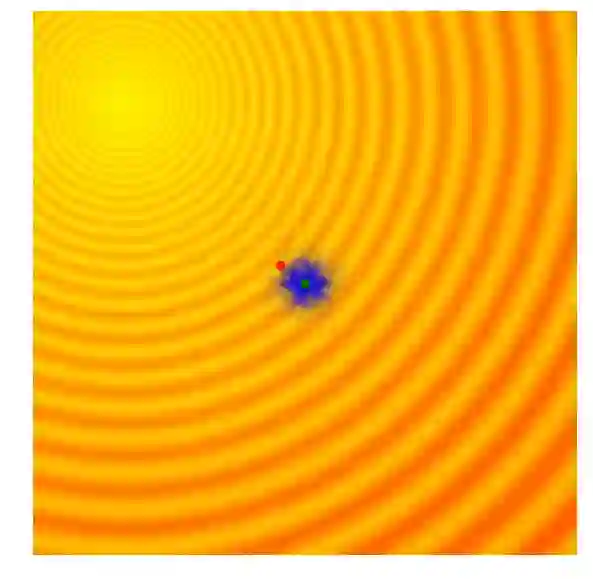
进化策略最简单的应用之一就是从一组服从高斯分布的随机数中抽取一组解，我们用μ来表示均值，用σ来表示固定标准差。以之前提到的玩具问题为例，在那两个问题中，μ=(μx ,μy )，σ=(σx ,σy)。刚开始的时候，我们把μ设置在图像原点，随着进化迭代，它不断找到最佳解决解并围绕这个新的均值进行抽样。

Schaffer函数图变化

Rastrigin函数图变化

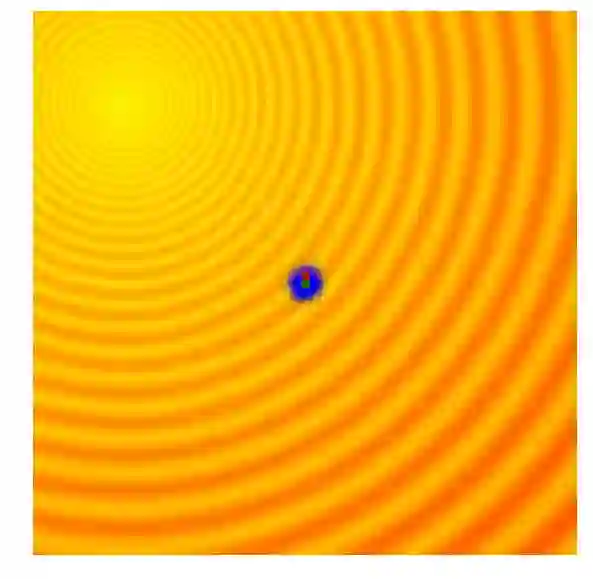
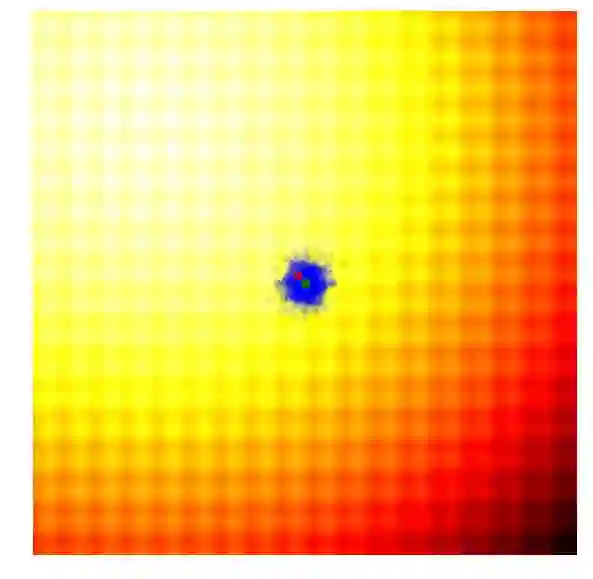
以上动图是函数经过20次迭代的变化情况，其中绿点表示每一代的新均值，蓝色图块是候选解，红点则是算法得到的最优值。

这个示例的简单算法通常只适用于简单问题，鉴于其贪婪的本质，它会抛弃除了最优解外的其他所有解，并且可能在面对复杂问题时生成局部最优值。因此，比起在具体某一代中寻找最优值，从多样性更丰富的上一代中根据概率分布采样进化出下一代会是一个更理想的方法。

遗传算法简介

谈到黑盒优化技技术，遗传算法是其中历史比较悠久的算法之一。随着研究的不断突破，如今遗传算法已经衍生出了许多复杂的版本，但在这里我们只讨论其中最简单的一种。

遗传算法的思路很简单，就是只保留当前这一代中一定比例，如前10%的最优解，然后舍去剩下的90%。在下一代，算法从上一代遗留下来的解中随机选择一对父本，并重组它们的参数形成一个新个体。这个从父本抽调参数的交叉重组过程类似抛硬币，是完全随机的（其实需要考虑近亲繁殖因素，但本文不涉及）。在我们的玩具问题中，这个新解继承父本x、y参数的概率各占50%，因此带有固定标准差σ的高斯噪声也会随着重组过程进入每个新的解。

Schaffer函数图变化

Rastrigin函数图变化

上图简单演示了遗传算法的工作情况，其中绿点表示上一代遗留下来的父本，蓝点是父本集的后代，而红点则是算法的到的最优值。

遗传算法通过跟踪不同解的参数来重建下一代，虽然一定程度上有利于解的多样性但在具体实践中，这种筛选最优解的做法也会面临最后结果收束到局部最优值的问题。因此，许多专家学者曾对它做过不少优化补充，如CoSyNe，ESP和NEAT，这些版本的想法是把种群中类似解的参数聚合到其他解中，以保持更优质的多样性。

协方差矩阵自适应演化策略（CMA-ES）

由以上实践可知，在我们的简单问题中，进化策略是遗传算法的缺点在于设定的标准差是固定的。有时候，我们想要探索更多空间，并上调标准差；有时候，我们认为算法已经接近了最佳值，希望能微调一下解。简单来说，我们心目中的算法搜索过程应该是这样的：

Schaffer函数图变化

Rastrigin函数图变化

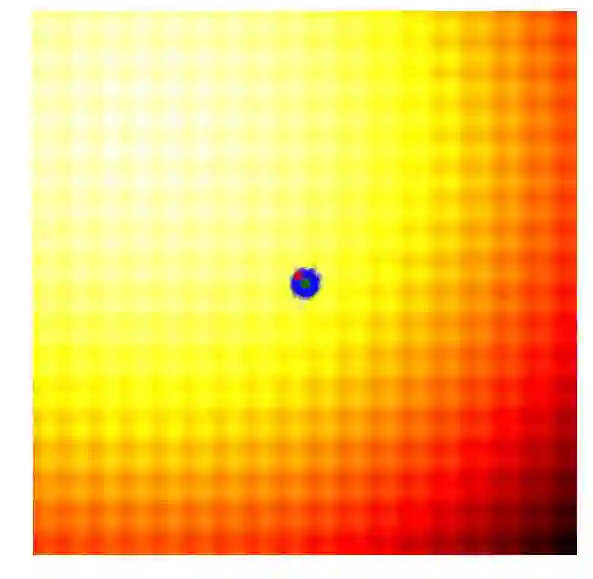
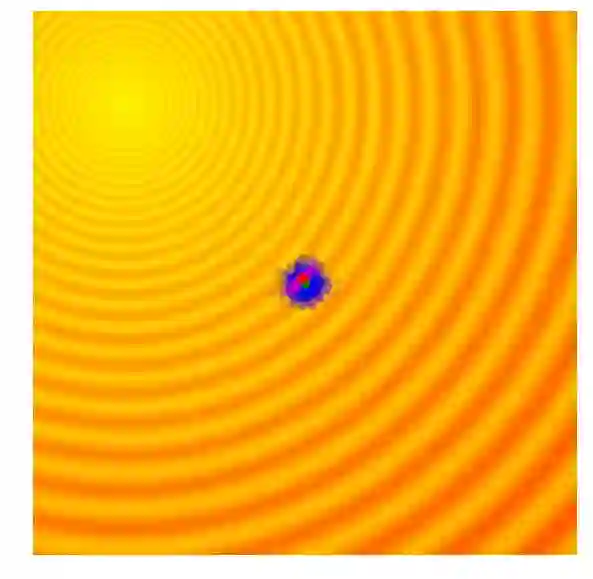
这样的效果令人惊叹！要想自己动手实现这一幕，你需要学习协方差矩阵自适应演化策略。协方差矩阵自适应演化策略是一种能够把握每一代结果，并自适应增加或减少下一代搜索空间的算法，它不仅能适应均值μ和标准差σ，还能计算整个参数空间的协方差矩阵。在每一代，CMA-ES提供了一个多变量正态分布参数的解的样本。那它是怎么做的呢？

在开始讨论它的方法前，一些简单的数学计算不可或缺。首先，我们要计算xi和yi：

其次，计算2x2协方差矩阵C：

当然以上得出的解只是个估计值，只能作为参考。为了简化计算，我们暂时把Nbest定为25%，即取前25%来更新参数，由g代进化出的下一代（g+1）的均值μg+1为：

最后，我们用25%来估计协方差矩阵Cg+1，需要注意的是，这里我们用的均值是μg，而不是μg+1：

有了μ_x、μ_y、σ_x、σ_y、σ_xy，我们就可以从（g+1）的参数中采样下一代解了。

1. 计算出每一代（g）每个候选值的适应值；

2. 从当前代（g）中分离出25%的最优值，在图中用紫色点表示；

3. 选取经分离后的最优值，结合当前代的均值μg，计算下一代矩阵Cg+1；

4. 用Cg+1和μg+1对新一代候选解抽样。

让我们再看一遍玩具问题中的整个搜索过程：

Schaffer函数图变化

Rastrigin函数图变化

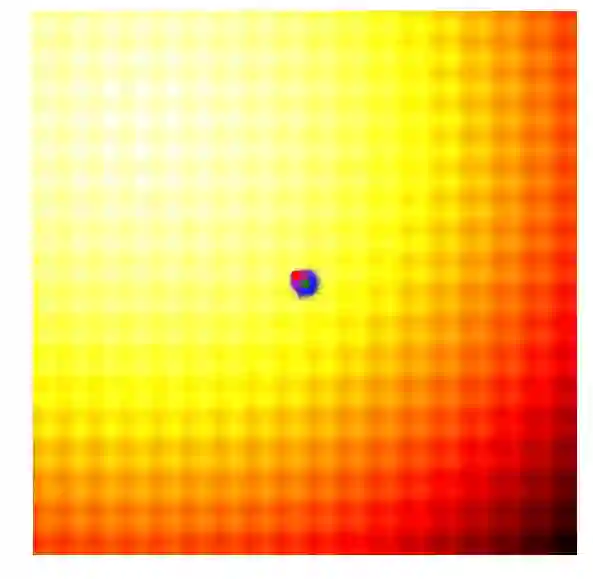
因为CMA-ES可以使用最佳值的信息自适应调整均值和协方差矩阵，所以当算法距离最佳值过远/过近时，它可以扩大/缩小搜索范围。我在上文中介绍了似然估计的计算方法，但考虑到入门新手还会有一些问题，在此我推荐CMA-ES发明人Nikolaus Hansen撰写的教程：https://arxiv.org/abs/1604.00772。

这个算法是现在最流行的无梯度优化算法之一，而且广受研究人员和数据科学从业者欢迎。如果要说缺点，那它唯一一点会被诟病的是性能。CMA-ES适合用于1000个参数以下的搜索空间，当然你如果愿意等，根据我的测试，10000个也是可以用的~

自然进化策略

试想一下，如果你已经建立了一个人工生命模拟器，并且选取了一系列不同的神经网络控制蚁群内每只蚂蚁的行为。通过简单的进化策略算法，你筛选出最有利于蚂蚁的特征和行为，并利用一代代演化过程巩固、优化这些特征。最后，你得到的只会是一群只想着自己如何更优秀的蚂蚁。

反之，如果把蚁群看做一个整体，计算整体的适应值来进行优化，那会产生更好的结果吗？答案显而易见，由于这些蚂蚁都没有经历“物竞天择，适者生存”，它们最后接受的只会是一个及时止损的“乌托邦”式结局，并不会向往比上一代更进一步。

结合上述所提及的算法，可以发现它们都有一个弱点，即放弃了大多数解，只保留最优值。其实那些不那么“优秀”的解中也包含了一些否定信息，它能提示not to do，这对于下一代得出一个更具价值的值是有意义的。

研究强化学习的人应该会对1992年的那篇经典论文Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning印象深刻，在文中，Williams推荐了一种通过预估神经网络梯度推测奖励的方法，在文章第六节，他还提出将强化用于进化策略。从那以后，相关研究持续推进，而Parameter-exploring Policy Gradients和Natural Evolution Strategies这两篇论文都是对REINFORCE-ES的经典扩展。

这种方法旨在使用来自每个成员的所有信息，无论好坏，它们都可以被用来估计一个梯度信号，并使整个种群在进化到下一代时能朝着更好的方向前进。由于需要预估梯度，我们可以灵活借用深度学习中随机梯度下降算法（SGD）的参数更新规则，让它服务于更精确的梯度计算。如果愿意，我们甚至可以用Momentum SGD、RMSProp或Adam。

它的思路是使候选解适应值的期望最大化，如果期望足够好，那么种群样本中最优值的期望应该更好，因此对期望进行优化可能是一个明智的做法。而实践也证明，最大化的样本期望和整个种群的总体适应值几乎相同。

如果样本z的概率密度函数为π(z,θ)，则可定义目标函数期望F为：

θ是函数的参数。当π为高斯分布时，θ即μ和σ。在我们的二维玩具问题中，每个z都是向量(x,y)。论文Natural Evolution Strategies对θ和J(θ)的梯度推导做了具体解释，借用REINFORCE的对数似然法，可计算J(θ)：

在一个大小为N的种群中，已知z1，z2，...zN，可用求和估计梯度：

有了∇θJ(θ)，则可用学习率（如0.01）开始优化参数。利用SGD（或Adam），我们可以计算θ的迭代：

这样即完成了一轮函数更新，在此基础上进行抽样迭代，最终我们会获得最优值。

在Williams论文的第六节，他还对梯度公式∇θ logπ(zi ,θ)进行推导，这主要是针对π(z,θ)是多变量高斯分布函数的情况（即参数为0）。在这种情况下，θ是μ和σ的向量，所有解都可从zj∼N(μj ,σj)中抽样得到。

对∇θ logπ(zi ,θ)求导：

其中j为参数空间，i为单个样本。在玩具问题中，z1 =x， z2 = y，μ1 =μx，μ2 =μy，σ1 =σx，σ2 =σy。利用上述公式，整个算法的运行状态如下图所示：

Schaffer函数图变化

Rastrigin函数图变化

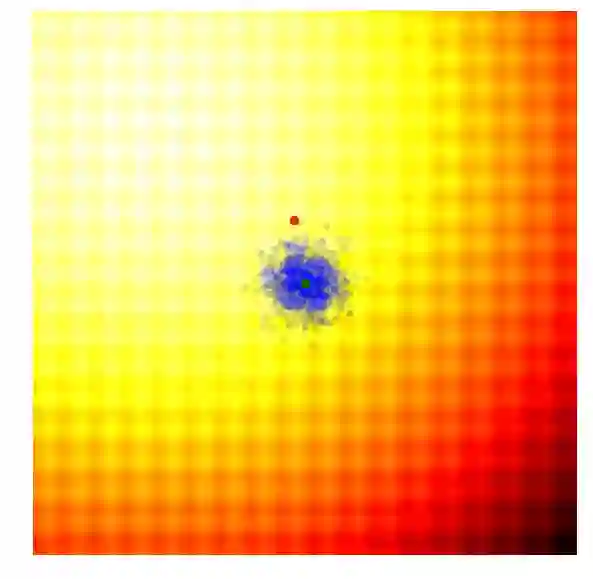
可以发现，这个算法能自适应调整搜索空间和对解进行微调，和CMA-ES不同，这个实现没有相关结构，因此我们无法得到对角椭圆样本，只有垂直或水平的样本。如果愿意降低计算效率，原则上我们可以导出更新规则来包含整个协方差矩阵。

OpenAI的进化策略

在OpenAI的论文中，他们实现了一个进化策略，这是之前提到的REINFORCE-ES算法中的一个特例，尤其是它的σ是个固定的常数，只有μ参数随着迭代更新。下图是OpenAI进化策略的大致情况：

Schaffer函数图变化

Rastrigin函数图变化

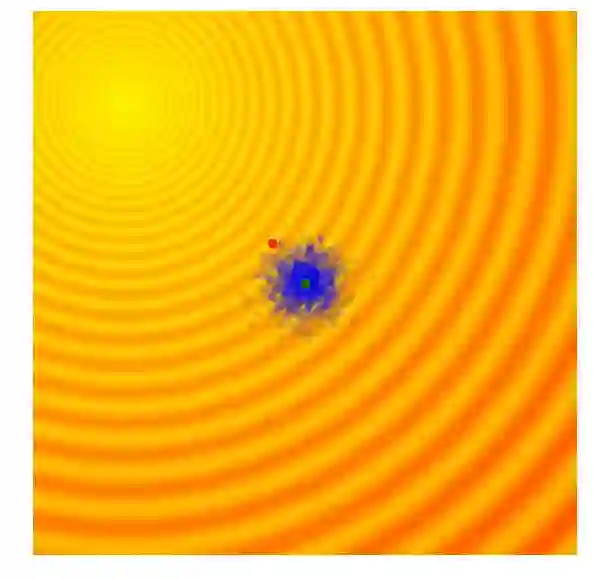
除了简化外，该文还提出对参数更新规则进行了修改，以适应不同机器并行计算。在这个新规则中，OpenAI用一个固定seed生成了一大堆随机数，这之后，机器间可以互相复制参数，它们只需进行简单的数字交流，即交换单个解的最终适应值。要知道，这对于用进化策略处理涉及上百甚至上千台机器并行计算的任务至关重要，因为如果要计算当前一代中的最佳函数向量，你可能需要进行上百万次数据传输，这在实际操作中并不可行。在论文中，OpenAI租用Amazon EC2云服务器上的1440个CPU在短短十分钟内就完成了MuJoCo训练。

我认为从原则上说，这个并行更新规则可以适应那个可以对σ做自适应调整的算法，也许OpenAI的考虑是在计算中尽可能让搜索更集中。无论如何，这篇文章值得一读。

Fitness Shaping

上述算法都结合了一种适应值调整、塑造的方法，即fitness shaping，它能帮我们规避种群中的异常值，避免得出过于相近的梯度，如之前的计算：

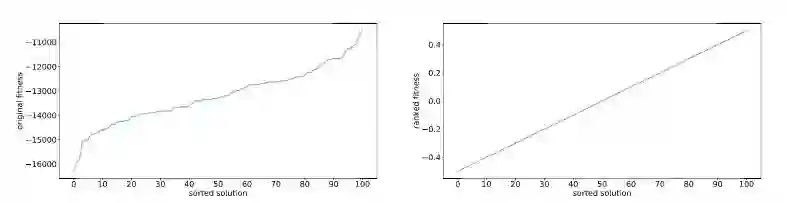
如果F(zi)中有一个过大的异常值 F(zm )，它可能会对样本梯度产生过大影响，使算法得出局部最优值。为了避免这一点，一种方法是对适应值进行等级变换，也就是说，算法不包含一个具体的适应值函数，它只对结果做评级，并引入一个和等级成正比的增强适应值函数。下图展示了两种操作带来的不同影响：

假如我们有一个规模为101的种群，我们需要计算其中每一个个体的实际适应值，然后根据适应值挑选解。例如，如果最低适应值的个体的评分是-0.50，倒数第二个体的评分是-0.49……那么排名第二的个体评分应该是0.49，而最佳的则为0.50。根据这个排名得出的增强适应值会在梯度计算中参与实际计算。

fitness shaping对强化学习问题有时也有奇效。如当给定神经网络中充满不确定因素，涉及一大堆随机maps和opponents时，它能显著提高整体效率。但如果那是一个确定的、行为良好的神经网络，那fitness shaping会拉低计算速率。

MNIST数据集

尽管进化策略能比基于梯度的算法得出更多样化的解，但在一些可以计算出高质量梯度的问题上，它还是明显落了下风。你会进化策略做图像分类吗？显然大多数回答是不会。但这个世界上也确实有一些“呆子”愿意吃力不讨好，更有甚者，他们还得出了丰硕的成果。

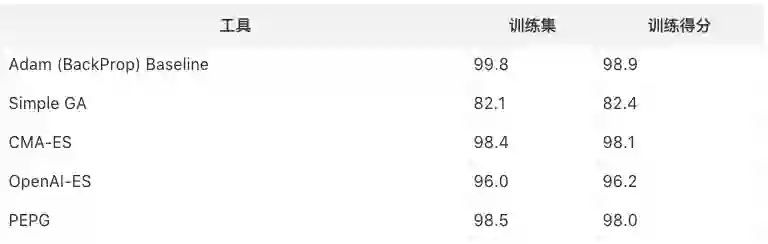
MNIST是机器学习算法适用的一个经典数据集，我曾利用进化策略在上面试着用一个小型的、只有2层的神经网络训练一个分类器，事实上这个做法的初衷在于观察随机梯度下降程度。由于包含的参数只有11000个，所以我用了效率比较低的CMA-ES算法。

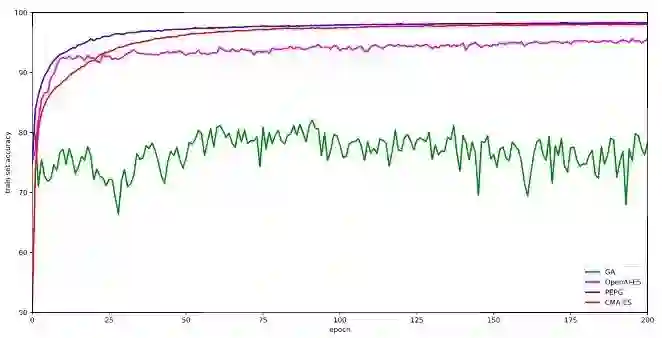
以下是我得出的结果：种群规模101，迭代300次。我跟踪了每一代结束时整个训练集上表现最佳的模型参数，并在完成300次迭代后又对模型进行了评估，在这之中我发现了一件有趣的事，有时测试集的准确率高于评分较低的训练集模型。

当然这个结果的可信度有待商榷，因为我只跑了一次，不是跑了五六次的平均值。但就这一次的表现来看，CMA-ES在MNIST上的表现很好，它和PEPG不相上下，准确率高达98%。也许正是因为它能对协方差矩阵做自适应调整，所以在权重计算上更精确。而OpenAI的简化版进化策略则表现一般。

动手试一试

本文提到的CMA-ES算法已有一些开源工具。据我所知，算法作者Nikolaus Hansen就有一个基于Numpy的CMA-ES开源工具，而且已经维护了一段时间，Python的他也有。如果你也想对比这几种算法的准确率，你可以使用我写的代码，并在这一行位置自定义修改：

import es
#solver = es.SimpleGA(...)
#solver = es.PEPG(...)
#solver = es.OpenES(...)
solver = es.CMAES(...)
while True:
  solutions = solver.ask()
  fitness_list = np.zeros(solver.popsize)
  for i in range(solver.popsize):
    fitness_list[i] = evaluate(solutions[i])
  solver.tell(fitness_list)
  result = solver.result()
  if result[1] > MY_REQUIRED_FITNESS:
    break

完整代码地址（es.py）：https://github.com/hardmaru/estool/blob/master/es.py

一些实例：https://github.com/hardmaru/estool/blob/master/simpleesexample.ipynb

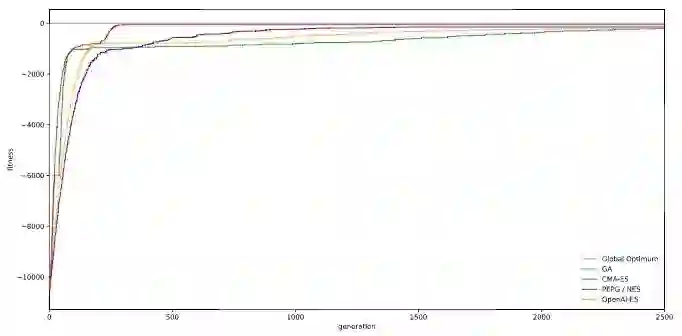
Rastrigin函数，是英雄就上100-D：https://github.com/hardmaru/estool/blob/master/simpleesexample.ipynb

100-D Rastrigin：各算法准确率对比

CMA-ES找到了最优解：向量10

注：为避免偷换概念，论智君将原文population一词译为“种群”，具体可结合情景理解；计算方法处涉及大量概率论知识，也已做简化处理。如发现错误，欢迎留言指明，谢谢~最后，再次感谢作者的热心分享~

原文地址：blog.otoro.net/2017/10/29/visual-evolution-strategies/

博主大トロ的其他文章：

零门槛教学：基于循环神经网络的建模思路

如果引进汉字的是循环神经网络，日本文字会是什么样