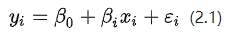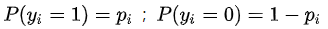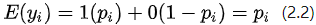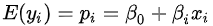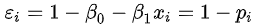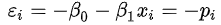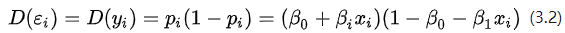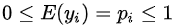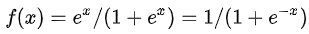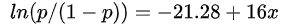逻辑斯蒂回归:家庭买私家车的概率
作者:herain R语言中文社区专栏作者
知乎ID:https://www.zhihu.com/people/herain-14
前言
我们讨论过因变量为数值型的一元线性和多元线性预测模型,今天我们来讨论定型变量的回归模型,定性变量可以说是一种类别变量,比如男/女,优/良/差,是/否,真/假,黑/白等,因变量的结果集是有限的,可预设的,定性变量的回归模型,就是基于历史数据训练出来一种数学表达式,来判断新数据的属于哪一种定性因变量的概率大小。为日常的常见的是否类决策,提供准确度的数值度量。
目录:
一,简述什么是定性因变量?
二,定性变量回归方程的意义?
三,定性因变量回归的特殊问题?
四,引入Logistic模型,解决定性因变量回归的特殊问题
五,Logistic模型实战
在许多社会经济问题中,所研究的因变量往往只有两个可能结果,这样的因变量也可用虚拟变量来表示,虚拟变量的取值可取0或1。0/1 对应现实意义的假/真,这是对多种因素触发结果的一种二分描叙。二分描述就是一种二分定性,定性结果集「0,1」或「假,真」。表示结果的变量,统称为定性变量,本质是分类变量。
设因变量y是只取0,1两个值的定性变量,考虑简单线性回归模型:
在这种y只取0,1两个值的情况下,因变量均值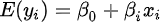
由于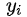
根据离散型随机变量期望值的定义,可得:
得到:
因变量均值y是自变量水平为x是y=1的概率。
对一个取值为0和1的因变量,误差项 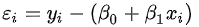
当 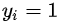
当 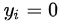
显然,误差项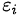
当因变量是定性变量时,误差项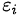
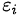
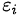
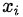
当因变量为0、1虚拟变量时,回归方程代表概率分布,所以因变量均值受到如下限制:
对一般的回归方程本身并不具有这种限制,线性回归方程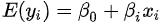
对于普通的线性回归所具有的上述3个问题,虽然可以找到一些相应的解决办法。例如,对于误差项不是正态的情形,最小二乘法求得的无偏估计量在绝大多数情况下是渐近正态的。因此,当样本容量较大时,未知参数的估计与误差项假设为正态分布时的方式相同;对于异方差情况,可以用加权最小二乘法来处理;对受回归方程限制的情况,对模型范围内的x来说,可以通过确保拟合模型的因变量均值不小于0和不大于1来处理。但是这些并不是从根本上解决问题的办法,为了从根本上解决问题,我们需要构造一个自动满足以上限制的模型来处理。
第一,回归函数应该改用限制在[0,1]区间内的连续曲线,而不能再沿用直线回归方程。
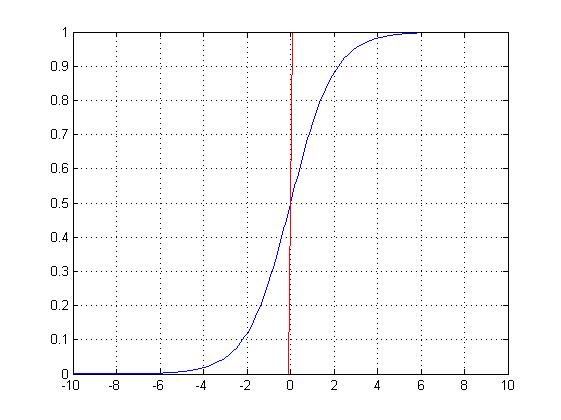
限制在[0,1]区间内的连续曲线有很多,例如所有连续型随机变量的分布函数都符合要求,我们常用的是Logistic函数与正态分布函数。Logistic函数的形式为 :
第二,因变量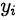
由于回归函数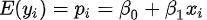
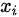
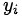
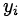
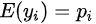
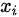
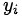
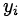
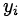
数据:某地区45个家庭数据的调查,其中y是分类变量(是否有私家车,1表示有,0表示没有)x 表示家庭年收入单位万元,根据这些数据建立Logistic回归模型,估计年收入15万元的家庭买私家车的可能性。
x y
15 1
20 1
10 0
12 1
8 0
30 1
6 0
16 1
22 1
36 1
7 0
24 1
6 0
11 0
18 1
25 1
12 0
10 0
15 1
7 0
22 1
7 0
16 1
18 1
21 1
7 0
9 0
6 0
20 1
16 1
12 0
15 1
9 0
基于R语言操作如下:
1> library(readxl)
2> data3.1 <- read_excel("/Users/MLS/desktop/多元统计基于R/eg3.1.xls",sheet=1)
3
4> glm.logit<-glm(y~x, family=binomial, data=data3.1)
5Warning message:
6glm.fit:拟合機率算出来是数值零或一
7> summary(glm.logit)
8
9Call:
10glm(formula = y ~ x, family = binomial, data = data3.1)
11
12Deviance Residuals:
13 Min 1Q Median 3Q Max
14-1.21054 -0.05498 0.00000 0.00433 1.87356
15
16Coefficients:
17 Estimate Std. Error z value Pr(>|z|)
18(Intercept) -21.2802 10.5203 -2.023 0.0431 *
19x 1.6429 0.8331 1.972 0.0486 *
20---
21Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
22
23(Dispersion parameter for binomial family taken to be 1)
24
25 Null deviance: 62.3610 on 44 degrees of freedom
26Residual deviance: 6.1486 on 43 degrees of freedom
27AIC: 10.149
28
29Number of Fisher Scoring iterations: 9
根据R计算我们得到回归模型函数:
计算 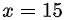
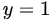
1> yp<-predict(glm.logit, data.frame=(x=15))
2> p.fit<-exp(yp)/(1+exp(yp));
3> p.fit
41
50.9665418
有R计算结果可知:年收入15万的家庭买私家车的概率为97%。
我们用Logistic回归模型成功地拟合了因变量为定性变量的回归模型,但是仍然存在一个不足之处,就是异方差性并没有解决,回归模型不是等方差的,应该对模型式用加权最小二乘估计。权重系数: 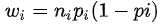
往期精彩:
公众号后台回复关键字即可学习
回复 爬虫 爬虫三大案例实战
回复 Python 1小时破冰入门
回复 数据挖掘 R语言入门及数据挖掘
回复 人工智能 三个月入门人工智能
回复 数据分析师 数据分析师成长之路
回复 机器学习 机器学习的商业应用
回复 数据科学 数据科学实战
回复 常用算法 常用数据挖掘算法
开工后的第一个周末就要到了,开心吧↓