博客 | 回归类算法最全综述及逻辑回归重点讲解

本文原载于微信公众号：AI部落联盟（AI_Tribe），AI研习社经授权转载。欢迎关注 AI部落联盟 微信公众号、知乎专栏 AI部落、及 AI研习社博客专栏。

大家肯定知道线性回归和逻辑回归，还有其他类回归吗？不同类回归是根据什么区分的？他们的使用场景、优缺点有什么不同？线性回归有什么关键问题？逻辑回归的适用性是什么？逻辑回归能不能用于多分类？用于互斥的多分类与不互斥的多分类时有什么不同？带着这些问题一起来学学回归吧。

1.回归家族

根据因变量的类型、目标变量的个数、回归函数线的形状，可以把回归分为7类：线性回归、逻辑回归、多项式回归、逐步回归、岭回归、Lasso回归、ElasticNet 回归。

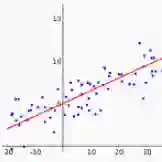
1.1线性回归：通过一条直线来拟合一个因变量Y与多个自变量(x1,x2...xn)的关系Y = a + W * X，自变量和因变量是线性关系。线性回归适用于低纬(自变量别太多)， 且每一维之间都没有共线性。

共线性、自相关、异方差、对异常值非常敏感、模型参数的估计很不稳定(样本数据微变，可能参数估计就会巨变)。

1.2逻辑回归:擅长于二分类，也可用于多分类，不要求自变量和因变量是线性关系

独立的变量不能有共线性、容易欠拟合、需大量样本、不能很好地处理大量的多类特征

1.3多项式回归:如果回归的自变量指数超过1，则称为多项式回归。它的图形是曲线。

适合非线性关系的回归关系，一般情况比线性回归拟合度更好，但也会过拟合。

1.4逐步回归:基于特定标准加入或移除变量来拟合回归模型。自动选择变量，不需人干预。

逐步回归的每一步都会添加或移除一些变量。包括前进法和后退法，前者始于最显著的变量然后逐渐增加次显著变量，后者始于所有变量，然后逐渐移除一些不显著变量。逐步回归可以看成一种降维方法，它可以用最少的变量去最大化模型的预测能力。

1.5岭回归:在线性回归的基础上加入一个预测误差项，预测误差项包括偏差和方差。

可以解决重共线性问题、不能将模型系数收敛为0、没有特征选择功能。

1.6 Lasso回归:和岭回归非常类似，只是预测误差项中方差不一样。

惩罚项能收敛到0、有特征选择功能、存在不一致的问题。

1.7 ElasticNet 回归:是岭回归和Lasso回归的权重和。

存在双重收敛、改善Lasso 的不一致性问题。

岭回归解决共线性问题，Lasso回归解决变量选择问题， ElasticNet回归解决不一致性问题。

2. 回归理论基础

3. 线性回归的两个关键问题

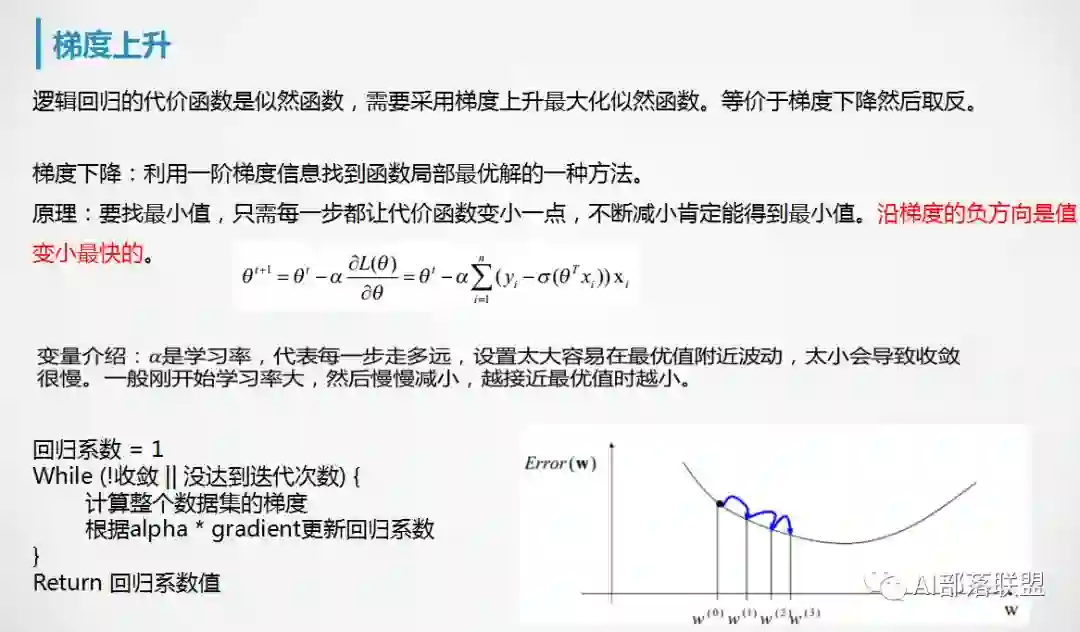
求解系数：最小二乘法和梯度下降法。

变量选择：逐步回归、最优子集法、正则化方法(包括岭回归、lasso回归)、降维(主成分回归、偏最小二乘回归)。

4. 逻辑回归的适用性

寻找关键因素(特征)：因为各个因素(特征)的贡献都是独立计算的，不需要条件独立性假设。

预测概率：尤其是广泛应用于广告点击率预测

广泛应用于各种场景下的分类：但是需要注意它一般仅能应用于线性问题，因此跟结果不是线性相关的feature一般都不起太大作用。

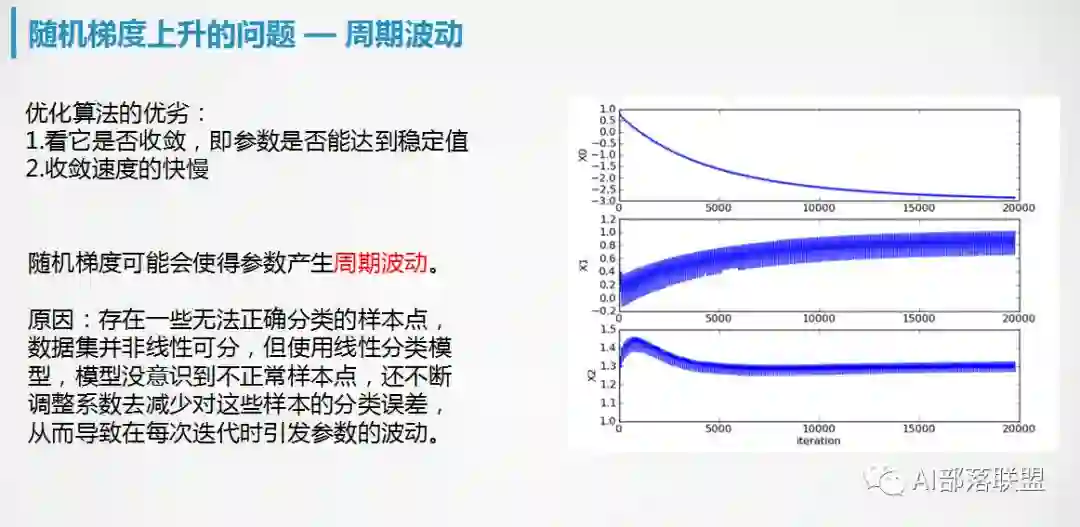
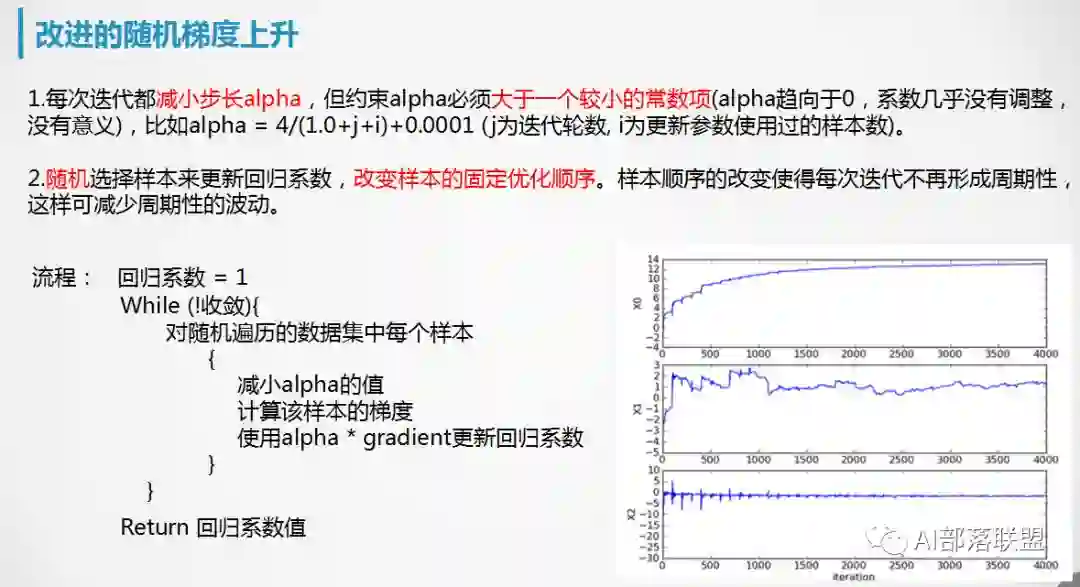
5. 逻辑回归的优化求解

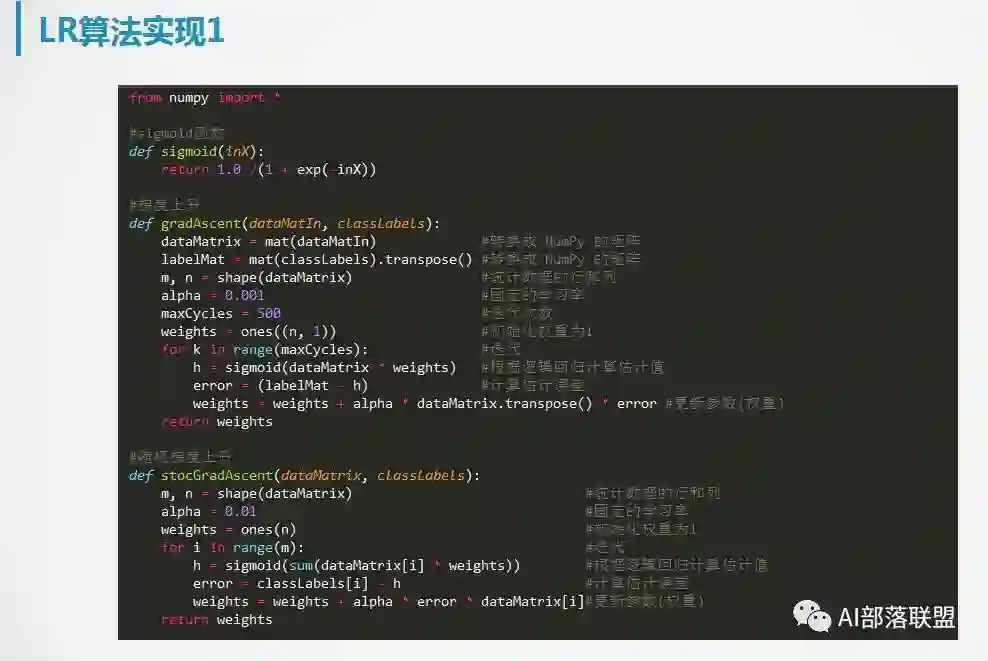
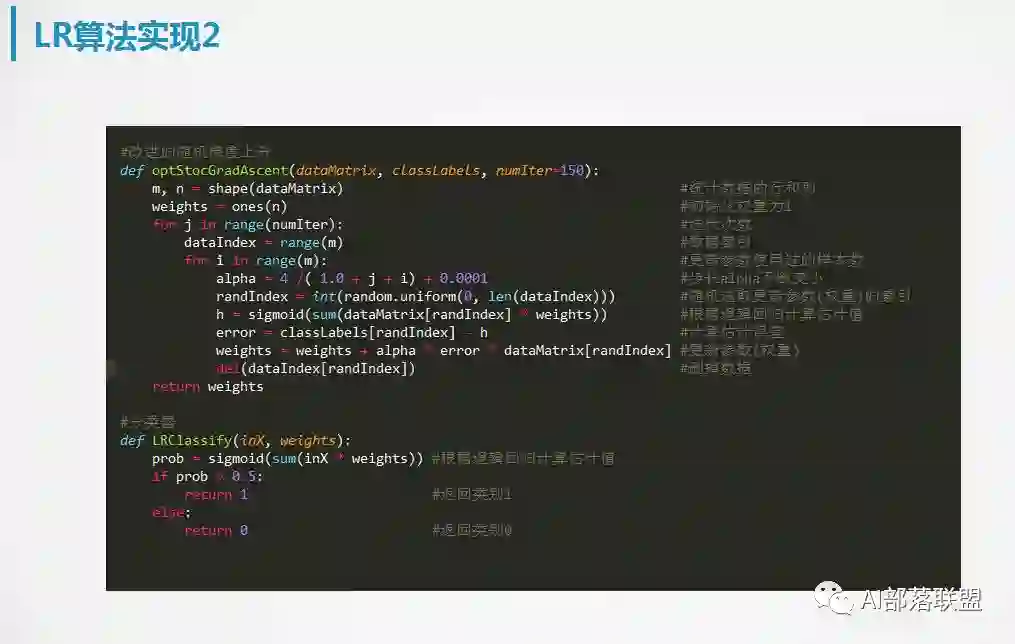
6. 逻辑回归的实现

 

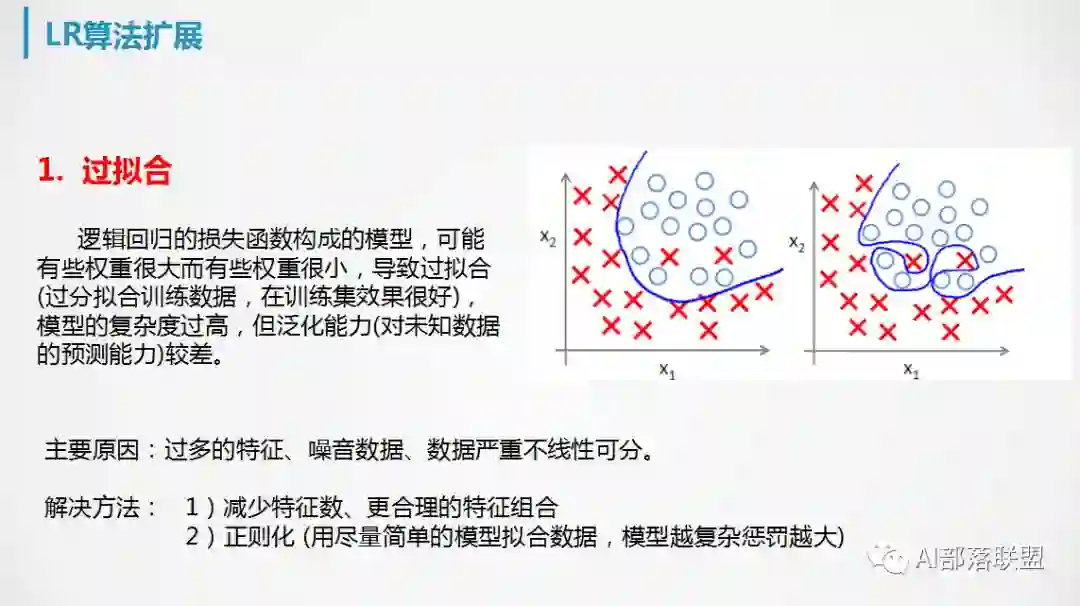
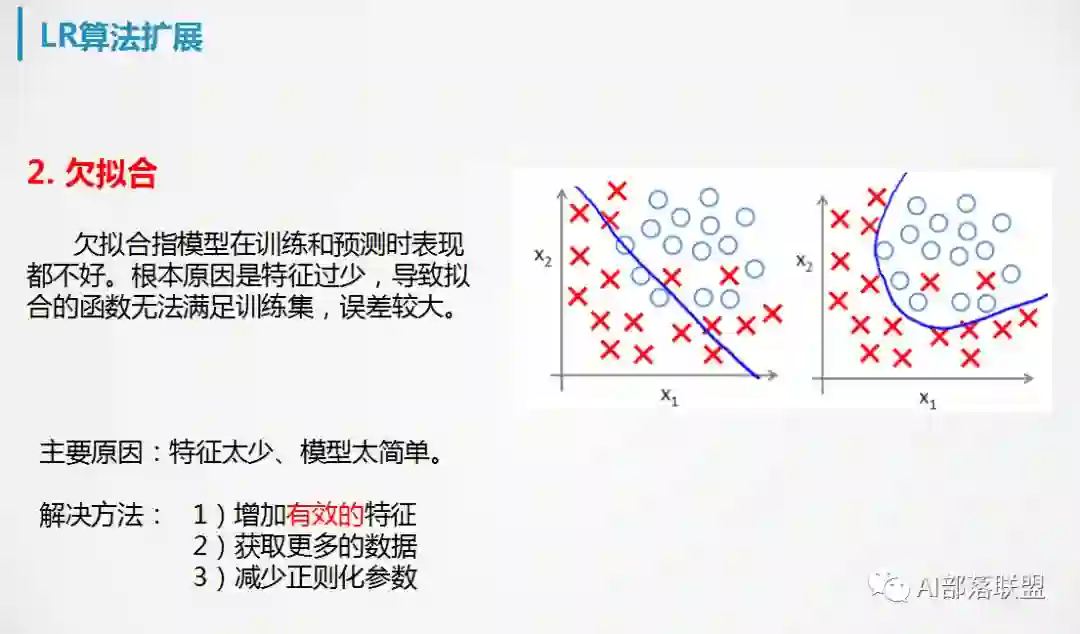
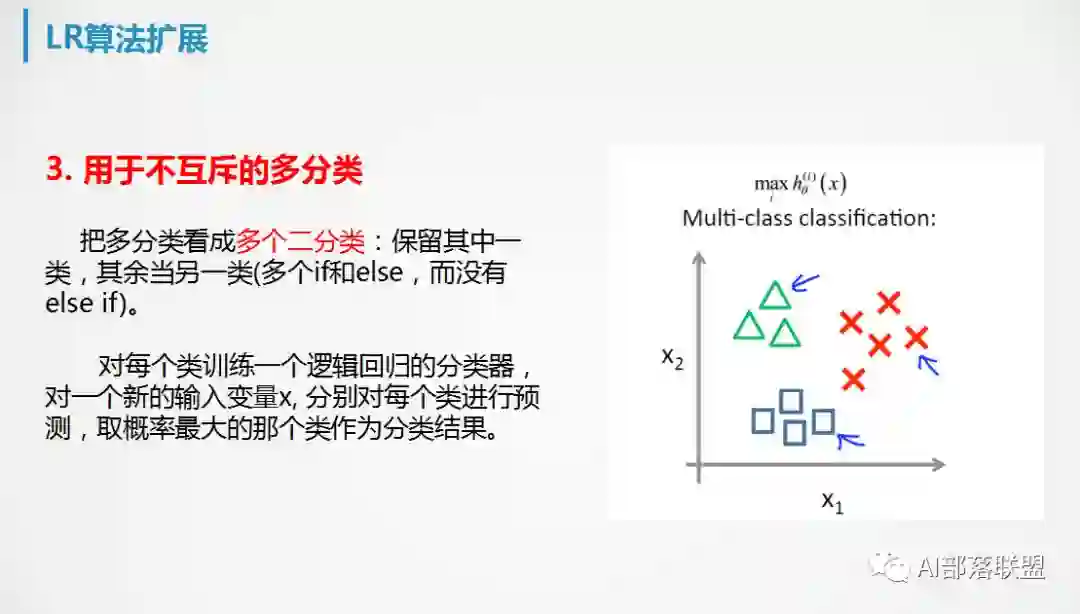
7. 逻辑回归的扩展

 

8. 总结

 

其实回归家族是个很庞大的家族，只是挑选我觉得比较关键的问题尝试简单分享，后续可能也会针对一些小的问题深入讲解，敬请期待~

 

后续我会专注于NLP（自然语言处理）、ML（机器学习）、DL（深度学习）、RL(强化学习)、TL(迁移学习)、GAN(生成对抗网络)等领域写一写个人的感悟，志在为大家提供一个干货与温度并存的学习与交流平台。期待您的关注，您的鼓励就是我不断写下去的动力，更期待有志同道合的朋友能加入一起写一写。予人玫瑰，手留余香！

独家中文版 CMU 秋季深度学习课程免费开学！

CMU 2018 秋季《深度学习导论》为官方开源最新版本，由卡耐基梅隆大学教授 Bhiksha Raj 授权 AI 研习社翻译。学员将在本课程中学习深度神经网络的基础知识，以及它们在众多 AI 任务中的应用。课程结束后，期望学生能对深度学习有足够的了解，并且能够在众多的实际任务中应用深度学习。

↗扫码即可免费学习↖

点击 阅读原文 查看本文更多内容↙