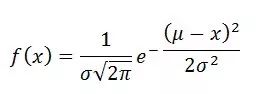为什么数据科学家都喜欢高斯分布

来源：Medium

编译：weakish

编者按：数据科学家Abhishek Parbhakar简洁明了地解释了机器学习中高斯分布如此受欢迎的原因。

对深度学习和机器学习工程师而言，在世界上所有的概率模型中，高斯分布（Gaussian distribution）模型最为引人注目。即使你从来没有进行过AI项目，有很大的几率你曾经遇到过高斯模型。

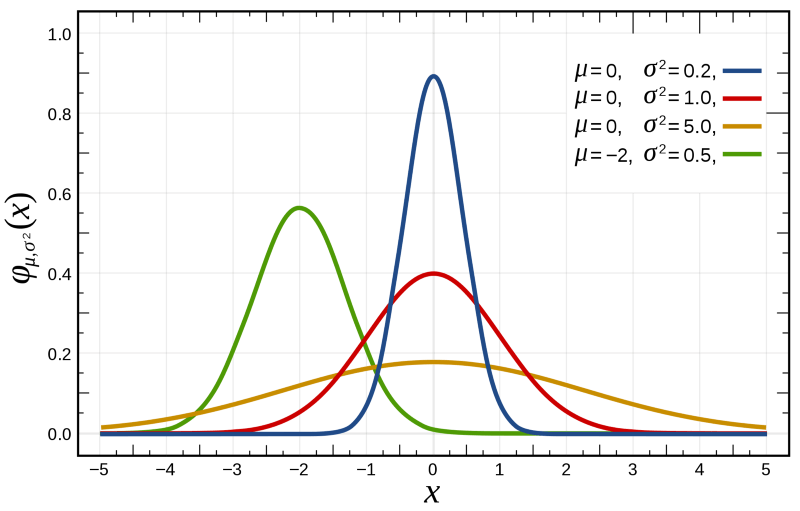
高斯分布，又称为正态分布（Normal distribution），常常可以通过其标志性的钟形曲线识别出来。高斯分布如此流行，有三大原因。

高斯概率分布函数

在自然现象中普遍存在

所有的模型都是错的，但有些模型有用！

—— George Box

扩散中的微粒的位置可以用高斯分布描述

自然科学和社会科学中有极其大量的过程天然遵循高斯分布。即使当它们并不遵循高斯分布的时候，高斯分布也往往提供最佳的逼近。一些例子：

• 成人的身高、血压、智商

• 扩散中的微粒位置

• 测量误差

数学上的原因：中心极限定理

二维平面随机行走两百万步

中心极限定理表明，满足一定条件时，大量相互独立的随机变量经适当标准化后，收敛于高斯分布。例如，随机行走的总距离分趋向于高斯概率分布。

这一定理意味着专门为高斯模型开发的大量科学方法和统计学方法同样适用于可能牵涉其他类型分布的广阔领域内的问题。

可以认为，这一定理解释了为什么这么多自然现象遵循高斯分布。

另外，高斯分布在一些转换后仍然是高斯分布：

• 高斯函数经傅里叶变换后，所得仍为高斯函数。

• 两个高斯函数的积仍然是高斯函数。

• 两个高斯函数的卷积仍然是高斯函数。

• 两个符合高斯分布的独立随机变量之和仍然符合高斯分布。

简单性

奥卡姆剃刀原则强调在其他条件相同时，最简单的解是最佳解

对每个高斯模型逼近而言，可能存在一个提供更好的逼近的复杂多参数分布。然而，我们仍然选择高斯模型，因为它大大简化了数学！

• 均值、中位数、众数均相等

• 整个分布仅需指定两个参数——均值和方差

高斯分布得名于伟大的数学家和物理学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）。

原文地址：https://towardsdatascience.com/why-data-scientists-love-gaussian-6e7a7b726859