「强化学习可解释性」最新2022综述

强化学习可解释性最新综述论文

强化学习是一种从试错过程中发现最优行为策略的技术，已经成为解决环境交互问题的通用方法.然而，作为一类机器学习算法，强化学习也面临着机器学习领域的公共难题，即难以被人理解.缺乏可解释性限制了强化学习在安全敏感领域中的应用，如医疗、驾驶等，并导致强化学习在环境仿真、任务泛化等问题中缺乏普遍适用的解决方案.为了克服强化学习的这一弱点，涌现了大量强化学习可解释性（Explainable Reinforcement Learning，XRL）的研究.然而，学术界对XRL尚缺乏一致认识.因此，本文探索XRL的基础性问题，并对现有工作进行综述.具体而言，本文首先探讨了父问题——人工智能可解释性，对人工智能可解释性的已有定义进行了汇总；其次，构建了一套可解释性领域的理论体系，从而描述XRL与人工智能可解释性的共同问题，包括界定智能算法和机械算法、定义解释的含义、讨论影响可解释性的因素、划分了解释的直观性；然后，根据强化学习本身的特征，定义了XRL的三个独有问题，即环境解释、任务解释、策略解释；之后，对现有方法进行了系统的归类，并对XRL的最新进展进行综述；最后，展望了XRL领域的潜在研究方向.

http://www.jos.org.cn/jos/article/abstract/6485

人工智能(Artificial Intelligence, AI)和机器学习(Machine Learning, ML) 在计算机视觉[1] 、自然语言处理 [2] 、智能体策略[3] 等研究领域都取得了突破,并逐渐融入人的生活.虽然 ML 算法对于很多问题具有良好表 现,但由于算法缺乏可解释性,模型实际使用中常受到质疑[4] [5] ,尤其在安全敏感的应用领域,如自动驾驶、医 疗等.缺乏可解释性的问题已经成为机器学习的瓶颈问题之一. 

强化学习(Reinforcement Learning, RL)被验证适用于复杂的环境交互类问题[6]-[8] ,如机器人控制[9] ,游 戏 AI[10] 等.但作为机器学习的一类方法,RL 同样面临着缺乏可解释性的问题,主要表现在如下 4 个方面: 

(1) 安全敏感领域中的应用受限.由于缺乏可解释性,RL 策略难以保证其可靠性,存在安全隐患.这一问题 在安全敏感任务(如医疗、驾驶等)中难以被忽略.因此,为避免模型不可靠带来的危险,RL 在安全敏感 任务中大多局限于辅助人类的决策,如机器人辅助手术[11] ,辅助驾驶[12] 等; 

(2) 真实世界知识的学习困难.虽然目前 RL 应用在一些仿真环境中具有优异表现,如 OpenAI gym[13] , 但这些仿真环境以简单游戏为主,与真实世界存在较大差异.另外,RL 应用难以避免对环境的过拟合. 当过拟合发生时,模型学到环境的背景信息,而非真正的知识.这导致了两难的问题,一方面,在真实世 界中训练 RL 模型通常消耗巨大,另一方面,难以确定在虚拟环境中训练的模型学到了真实的规律. 

(3) 相似任务的策略泛化困难.RL 策略通常与环境存在强耦合,难以被应用到相似环境中.甚至在同样的 环境下,环境参数的微小变化也会极大影响模型性能.这一问题影响了模型的泛化能力,难以确定模 型在相似任务中的表现. 

(4) 对抗攻击的安全隐患难于应对.对抗攻击[14] 是一种针对模型输入的攻击技术,通过将微小的恶意扰 动加入到模型的输入中生成对抗样本.对人而言,对抗样本不影响判断,甚至难以察觉,然而对于模型 而言,对抗样本会使模型的输出产生极大的偏差.对抗攻击从深度学习扩展到 RL[15] [16] ,成为 RL 算 法的安全隐患.对抗攻击的有效性进一步暴露了 RL 缺乏可解释性的问题,同时也进一步说明 RL 模 型并未学到真正的知识. 

解释对模型的设计者和使用者都具有重要的意义.对于模型的设计者,解释能体现模型所学的知识,便于 通过人的经验验证模型是否学到鲁棒的知识,从而使人高效地参与到模型的设计和优化中;对于特定领域的专 家使用者,解释提供模型的内部逻辑,当模型表现优于人时,便于从模型中提取知识以指导人在该领域内的实 践.对于普通用户,解释呈现模型的决策的原因,从而加深用户对模型的理解,增强用户对模型的信心.

强化学习可解释性(Explainable Reinforcement Learning, XRL),或可解释强化学习,是人工智能可解释性 (Explainable Artificial Intelligence, XAI)的子问题,用于增强人对模型理解,优化模型性能,从而解决上述缺乏可 解释性导致的 4 类问题. XRL 与 XAI 之间存在共性,同时 XRL 具备自身的独特性.

一方面，XRL 与 XAI 存在共性.首先,提供解释的对象是智能算法而非机械算法.机械算法,如排序、查找 等,其特点是完备的输入,固定的解法以及明确的解.而智能算法因为输入的不完备以及解法的不确定,导致算 法必须在解空间中寻找较优的解;其次,人和模型是两个直接面对的关键实体.与其他技术不同,可解释性方法 关注人对模型的理解.由于人对大量条例混乱的数据缺乏理解,因此解释通常对模型内在逻辑的抽象,这一过程 必然伴随对模型策略的简化.其中的难点是,如何在向人提供解释时,保证该解释与模型主体逻辑的一致性;最 后,解释的难度是相对的,同时由问题规模和模型结构两个因素决定,并且这两个因素在一定条件下相互转化. 例如,结构简单的模型(如决策树、贝叶斯网络等)在通常可以直观的展示输入和输出之间的逻辑关系,但面对由 大量简单结构组成的庞大模型,其错综复杂的逻辑关系仍然导致模型的整体不可理解.同时,虽然结构复杂的模 型(如神经网络)通常难以被理解,但当模型被极致约减时(如将神经网络塌缩为具有少数变量的复合函数),模型本身仍然可以被人所理解。

另一方面,XRL 也具备自身的独特性.强化学习问题由环境、任务、智能体策略三个关键因素组成,因此, 解决 XRL 问题必须同时考虑这三个关键因素.由于 XRL 的发展仍处于初步阶段,大部分方法直接从 XAI 的研 究中继承,导致现有研究集中于对智能体策略的解释,即解释智能体行为的动机及行为之间的关联.然而,缺乏 对环境和任务的认识使得一些关键问题无从解决:缺乏对环境的认识使人在面临复杂任务时,缺乏对环境内部 规律的理解,导致对环境状态进行抽象时忽略有利信息,使智能体难以学到真实的规律;缺乏对任务的解释使任 务目标与过程状态序列之间的关联不明确,不利于智能体策略与环境的解耦合,影响强化学习智能体策略在相 似任务或动态环境中的泛化能力.因此,对环境、任务和策略的解释存在强关联,是实现强化学习解释必然面临 的问题. 

目前,XRL 已经成为 AI 领域的重要议题,虽然研究者们为提高强化学习模型的可解释性做出了大量工作, 但学术界对 XRL 尚且缺乏一致的认识,导致所提方法也难以类比.为了解决这一问题,本文探索 XRL 的基础性 问题,并对现有工作进行总结.首先,本文从 XAI 出发,对其通用观点进行总结,作为分析 XRL 问题的基础;然后, 分析 XRL 与 XAI 的共同问题,构建出一套可解释性领域的理论体系,包括界定智能算法和机械算法、定义解释 的含义、讨论影响可解释性的因素、划分解释的直观性;其次,探讨 XRL 问题的独特性,提出包括环境解释、任 务解释和策略解释的三个 XRL 领域的独有问题;随后,对现有 XRL 领域的研究进展进行总结.以技术类别和解 释效果为依据将对现有方法进行分类,对于每个分类,根据获取解释的时间、解释的范围、解释的程度和 XRL 的独有问题,确定每类方法的属性;最后,展望了 XRL 领域的潜在研究方向,重点对环境和任务的解释、统一的 评估标准两个方向进行展开.

1 人工智能可解释性的观点总结 

对 XRL 的研究不能脱离 XAI 的基础.一方面,XRL 是 XAI 的子领域,其方法和定义密切相关,因此 XRL 的 现有研究广泛借鉴了 XAI 在其他方向(如视觉)的成果;另一方面,XRL 目前仍处于起步阶段,对其针对性的讨论 较少,而对于 XAI,研究者们长期以来进行了广泛的研究和讨论[17] -[24] ,具有深刻的借鉴意义.基于上述原因, 本文从 XAI 的角度探讨可解释性问题,整理出学术界对 XAI 的共识,以此作为 XRL 的研究基础. 

虽然学者们从不同角度对 XAI 的定义在特定情况下指导着一类研究.然而,缺乏精确而统一的定义使得学 术界对 XAI 的认识存在一定差异.本文对 XAI 相关的定义进行总结,并将其分为形而上的概念描述、形而下的 概念描述两类. 

形而上的概念描述使用抽象概念对可解释性进行定义[25] -[28] .这些文献使用抽象的词描述可解释性算法,例如可信性(trustworthy),可靠性(reliability)等.其中可信性意味着人以较强的信心相信模型所做的决定,而可 靠性意味着模型不同场景下总是能保持其性能.虽然这样抽象的概念不够精确,只能产生直观的解释,但仍然可以使人准确了解可解释性的目标、对象和作用,建立对可解释性的直觉认知.这些概念表明,可解释性算法具备 两个关键实体,即人和模型.换而言之,可解释性是一项以模型为对象,以人为目标的技术. 

形而下的概念描述从哲学、数学等的观点出发,基于解释的现实意义对其进行定义.如 Páez 等人[17] 从哲 学角度出发,认为解释所产生的理解并不完全等同于知识,同时理解的过程也不一定建立在真实的基础上.我们 认为,解释作为媒介存在,这个媒介通过呈现模型的真实知识或构建虚拟逻辑的方式,增强人对模型的理解.同 时,人对模型的理解不必建立在完全掌握模型的基础上,只要求掌握模型的主要逻辑,并能对结果进行符合认知 的预测. Doran 等人[29] 认为,可解释性系统使人们不仅能看到,更能研究和理解模型输入和输出之间的数学映 射. 一般而言,AI 算法的本质是一组由输入到输出的数学映射,而解释则是将这样的数学映射以人类可理解和 研究的方式展现出来.虽然数学映射也是人们为描述世界而创造的一种方式,但对于复杂的数学映射(如用于表 示神经网络的高维多层嵌套函数),人们却无法将其与生活中的直观逻辑相联系. Tjoa 等人[19] 认为,可解释性 是用于解释算法做出的决策,揭示算法运作机制中的模式以及为系统提供连贯的数学模型或推导.这一解释也 基于数学表达,反映出人们更多地通过模型的决策模式来理解模型,而非数学上的可重现性.

一些观点与上述文献存在微小出入,但仍具有借鉴意义.例如,Arrieta 等人[21] 认为可解释性是模型的被动 特征,指示模型被人类观察者理解的程度.这个观点将模型的可解释性视为被动特征,忽略了模型为了更强的可 解释性而主动提出解释的可能. Das 等人[23] 认为,解释是一种用于验证 AI 智能体或 AI 算法的方式.这一观点 倾向于关注模型的结果,其目的是为了确保模型一贯的性能.然而该描述忽略了一个事实,即模型本身意味着知 识,可解释性不仅是对模型结果的验证,同时也有助于从模型中提取人们尚未掌握的知识,促进人类实践的发 展.虽存在较小出入,但上述观点也提出了独特的角度,例如,可以将模型的可解释性视为模型的一个特性,而评 估模型的性能是解释的重要功能. 

虽然对 XAI 的定义众多,但就整体而言,学术界对 XAI 的基本概念仍然是一致的.本文尝试提取其中的共 性作为研究 XRL 问题的理论基础.通过对以上文献的分析,我们总结出学术界对 XAI 的共识: 

(1) 人与模型是可解释性直接面对的两个关键的实体,可解释性是一项以模型为对象,以人为目标的技 术; 

(2) 解释作为理解的媒介存在,该媒介可以是真实存在的事物,也可以是理想构建的逻辑,亦或是二者并 举,达到让人能够理解模型的目的; 

(3) 人的对模型的理解不需要建立在完全掌握模型的基础上;

(4) 可准确重现的数学推导不可取代可解释性,人对模型的理解包括感性和理性的认知;

(5) 可解释性是模型的特性,这一特性可用于验证模型的性能.

2 强化学习可解释性与人工智能可解释性的共同问题 

在对 XAI 定义进行总结的基础上,本节讨论 XRL 与 XAI 面临的共同问题.由于 XRL 与 XAI 之间存在强 耦合,因此本节内容既适用于 XAI,同时也是 XRL 的基础问题. 

2.1 智能算法和机械算法界定 

可解释性的对象是智能算法而非机械算法.传统认知中的机械算法,如排序、查找等,面对确定的任务目标, 同时具有固定的算法程序.强化学习作为一种智能算法,在与环境动态交互的过程中寻找最优的策略,最大化获 得的奖赏.界定智能算法和机械算法可用于确定被解释的对象,进而回答“什么需要被解释”的问题.一方面,智能 算法与机械算法存在差异,而解释只在面向智能算法时存在必要性;另一方面,即使对于强化学习,也无需对其 所有过程产生解释,而应针对其具有智能算法特性的部分进行解释,如动作生成、环境状态转移等.因此,在讨论 可解释性问题前,有必要区分智能算法和机械算法. 

本文根据算法对已知条件的获取程度和建模的完整性,定义“完全知识”和“完全建模”: 

完全知识:已知足够任务相关的有效知识,具备以机械过程获得最优解的条件; 

完全建模:进行完整的问题建模,具备完成任务所需的计算能力; 

完全知识是以机械方法确定最优解的前提.例如,求解系数矩阵的秩为 的线性方程组,完全知识表示其增 广矩阵的秩大于等于系数矩阵的秩,此时可以根据当前知识,获得确定的解或者确定其无解;完全建模意味着对 现有知识的充分利用,换言之,完全建模从建模者的角度出发,表示在解决任务的过程中有能力(包括程序设计 者的设计能力和硬件的算力)利用所有的知识.例如,在 19×19 围棋游戏中,存在理论上的最优解法,但目前尚不 具备足够的计算能力在有限时间内获取最优解. 

根据上述对完全知识和完全建模的定义,本文进一步提出“任务完全”的概念来确定机械算法与智能算法 之间的边界: 

任务完全:对特定任务,具备完全知识并进行完全建模. 

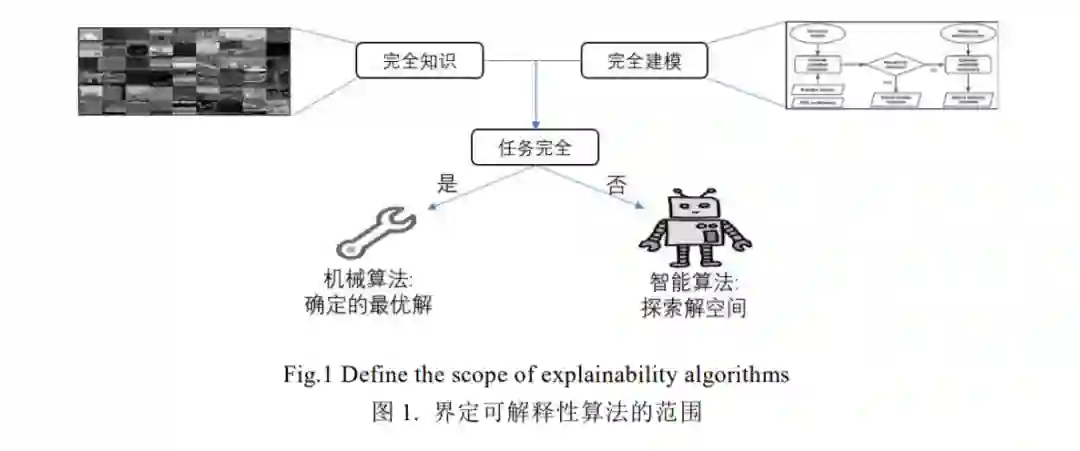
任务完全必须在完全知识的前提下进行完全建模.满足任务完全的条件后,算法的优劣取仅决于建模方式 和使用者的实际需求.任务完全的定义考虑了知识和建模两方面因素(图 1). 

任务完全的概念可以用来区分机械算法和智能算法.机械算法是任务完全的,具体来说,算法已知足够的 知识,并进行了无简化的建模.此时,算法具备获取最优解的条件,因此算法的过程是确定的,获得的解也是可预期的.例如,经典排序算法、传统数据查询、3×3 井字棋游戏算法等都属于机械算法.智能算法是任务不完全的, 这意味着算法不具备足够的知识,或者采取了简化的建模方式.智能算法无法直接获取最优解,通常在解空间中 寻找较优的解.如基于贪心策略的算法,线性回归方法,19×19 传统围棋策略,机器学习类算法等。

导致任务不完全的可能有二,即知识不完全和建模不完全.在知识不完全的情况下,算法无法直接确定最 优解,因此只能在解空间中逼近最优解.此时,智能算法的实际作用是在解空间中进行解的选择.导致知识不完 全的因素通常是客观的,如环境状态无法被完全观测,任务目标不可预知,任务评价指标的不可知,任务始终点 不可知等等;在建模不完全的情况下,算法通常忽略某些知识,导致算法过程没有充分利用知识,从而无法获得 最优解.建模不完全的原因有客观和主观两方面,客观原因如建模偏差,不完全建模等,主观原因包括降低硬件 需求,模型提速等.在强化学习中,并非所有过程具备任务不完全的特点,因此只有部分需要进行解释,如策略生 成、环境状态转移等.

2.2 对“解释”的定义 

在汉语词典中,解释有“分析、阐明”的含义.这不仅符合生活中对该词的理解,同时也与可解释性研究中“解 释”的含义相近.然而,具体到可解释性的研究中,这一含义显得宽泛.我们希望结合对可解释性的理解,细化“解 释”的含义,使之具有更强的指导意义.以强化学习模型为例,模型学习使奖励最大化的策略,其中包含着环境、奖 励和智能体之间的隐式知识,而 XRL 算法则是将这些隐式知识显式地表现出来.本文将多个知识视为集合,称 为知识体系,从知识体系相互之间关系的角度,对“解释”做出如下定义: 

解释:知识体系之间的简洁映射.简洁映射是在不引入新知识的条件下对目标知识进行表达; 

具体来说,解释是将基于原知识体系的表达转换为目标知识体系表达的过程,这个过程仅使用目标知识体 系的知识,而不引入新的知识.而 XRL 算法的目的在于产生解释,从而使原知识体系能够被目标知识体系简洁 的表达出来.在 XRL 中,原知识体系通常指代强化学习模型,而目标知识体系通常指人的认知,模型和人是可解 释性的两个关键实体.本文将原知识体系看作由多个元知识及其推论构成的集合.以 表示元知识, 表示知识 体系,则 .假设智能体习得的知识属于知识体系 ,而人类能够理解的知识属于知识体系 ,则解释 是将知识体系 转换为知识体系 表达的过程.对于解释而言,简洁映射是必要的,非简洁的映射可能提升解释 本身的被理解难度,进而导致解释本身让人无法理解(见 2.3 ). 

在对知识进行转换表达的过程中,待解释的知识可能无法完全通过目标知识体系进行描述,这时只有部分 知识可以被解释.本文使用“完全解释”和“部分解释”的概念描述这一情况:

完全解释:待解释的知识完全被目标知识体系表达.其中,被解释的知识属于目标知识体系是其必要条件; 

部分解释:待解释的知识的部分被目标知识体系表达.

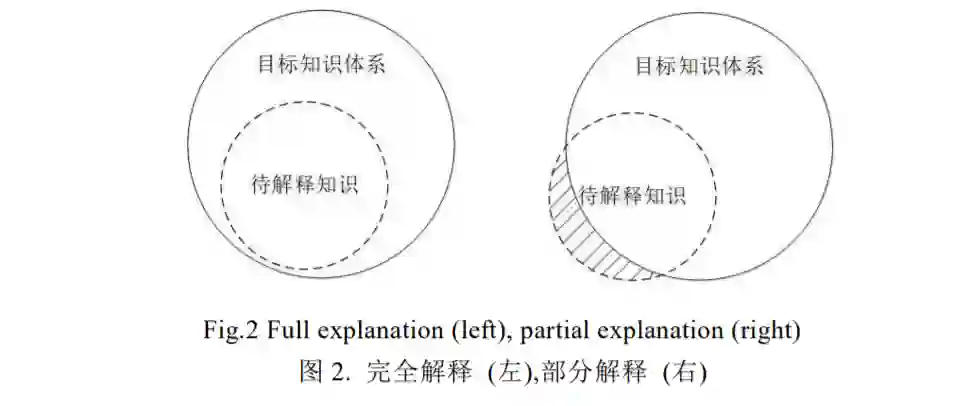
具体来说,完全解释和部分解释描述的是知识体系之间的包含情况(图 2).只有当待解释的知识体系完全 被目标知识体系所包含时,才可能进行完全解释,否则只能进行部分解释.在 XRL 中,完全解释通常是不必要的.

一方面,待解释知识体系和目标知识体系的边界难以确定,导致完全解释难度高且耗费巨大;另一方面,实现对 模型的解释通常不需要建立在对模型完全掌握的基础上.因此,部分解释是大部分可解释性研究中采用的方法, 即只描述算法的主要决策逻辑.

2.3 可解释性的影响因素 

一个观点认为,传统 ML(RL 为其子集)方法是易于解释的,而深度学习的引入使得可解释性产生了短板,导 致 ML难于解释,因此 ML 解释的本质是对深度学习的解释[21] .这与可解释性领域的认知相悖[28] .这一观点只 关注模型而忽略了人在可解释性中的地位.对于人而言,即使是理论上可被理解的模型,当规模扩张到一定程度 时,仍然会导致整体的不可理解.本文对可解释性的影响因素进行如下定义: 

透明度:待解释模型结构的简洁程度; 

模型规模:待解释模型包含的知识量和知识组合多样化程度; 

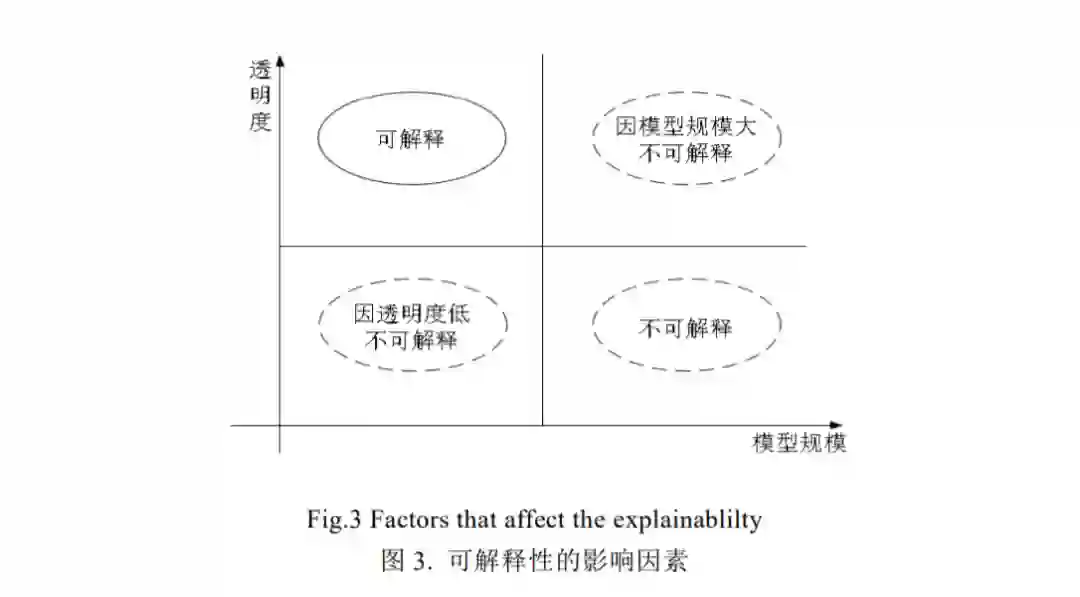
本文认为,可解释性是对模型组件透明度和模型规模的综合描述.透明度和模型规模是影响可解释性的两 个主要因素.具体来说,可解释性强意味着同时具备高透明度和低复杂度,而单一因素,如复杂度高或透明度低 将导致模型的弱可解释性(图 3). 

在不同语境下,“透明”一词具有不同的含义.例如,在软件结构中,透明指的是对底层过程的抽象程度,意味 着上层程序无需关注底层的实现.类似的,透明度在可解释性领域也存在不同的含义,如文献[26] [27] 认为透明 度是模型可以被理解的程度,将透明度与可解释性等价.以强化学习为例,基于值表的强化学习算法在规模一定 时通常具有更强的可解释性,而使用深度学习拟合值表则可解释性更弱,这是因为通过查询值表而产生策略的 过程符合人的直观理解,但神经网络传播过程仅在数学上可被准确描述,于人而言透明度更低.然而,这一思考 将构建模型的基础结构作为可解释性的重点,而忽略了模型规模对解释带来的难度,并忽略了解释的目标—— 人.因此,为突出模型规模对解释的影响,我们仅将透明度狭义理解为待解释模型的结构的简洁程度. 

模型规模从人理解能力的角度衡量解释的难度.具体来说,假设模型中的知识由一系列元知识构成,则模 型规模表示元知识总量和知识之间组合的多样化程度,而解释的难度一定程度上取决于模型规模,当模型规模 超过特定范围(人的理解能力)时模型将无法被理解.例如,线性加性模型、决策树模型、贝叶斯模型,由于计算过 程简洁,使我们能够轻易了解模型基于何因素得到何种结果,因此被认为是易于理解的.然而,当模型规模逐渐 庞大时,各因素之间的逻辑不可避免地相互交织,变得错综复杂,使我们最终无法抓住其主从关系.对于以简洁 结构(如决策树分支)构成的大规模模型,虽然所有结果在理论上有迹可循,但当模型规模已超越人类的理解能 力,导致系统整体将仍然不具备可解释性.

2.4 可解释性的程度划分 

人的学习过程与强化学习过程存在一定的相似性,因此,如果将人脑看作目前最先进的智能模型,则人对 模型的理解不仅仅是人对模型的直观感受,也是一个先进的智能体对强化学习模型的综合评估.然而,一个无法 理解的模型不可能被有效评估,因此对模型的解释成为人理解模型的媒介.作为人和模型之间媒介,可解释性算 法不同程度的具备两个相互平衡特点:接近模型和接近人的感知.具体来说,不同的解释有的更注重准确的描述 模型,而另一些更注重与人的感知一致.基于这一概念,本文将可解释性分为如下三个层次:

(1) 数学表达: 通过理想化的数学推导解释模型.数学表达是使用数学语言简化模型的表达.由于强化学 习模型建立在数学理论的基础上,因此通过数学表达可以准确地描述和重构模型.虽然数学理论体 系是人描述世界的一种重要方式,但其与人的普遍直觉之间存在较大差异.以深度学习为例,虽然存 在大量文章论证了其在数学上的合理性,但深度学习方法仍然被认为是不可解释的.因此,数学的表 达能够在微观(参数)层面对模型进行描述,但难以迁移至人类知识体系;

(2) 逻辑表达: 通过将模型转换为显性的逻辑规律解释模型.逻辑表达是对模型中主体策略的提取,即忽 略其细微分支,凸显主体逻辑.一方面,逻辑表达保留了模型的主体策略,因此与模型真实决策结果相 近,解释本身可以部分重现模型的决策;另一方面,逻辑表达简化了模型,符合人的认知.逻辑表达是较 为直观的解释,但需要人具备特定领域的知识,是面对人类专家的解释,而对一般用户尚不够直观; 

(3) 感知表达: 通过提供符合人类直觉感知的规律解释模型.感知表达基于模型生成符合人类感知的解 释,由于不需要人具备特定领域的知识,因此易于理解.例如,可视化关键输入、示例对比等解释形式 都属于感知表达的范畴.然而,感知表达通常是对模型策略的极大精简,因为无法重现模型的决策,导 致其只解释决策的合理性. 

在可解释性的三个层次中,数学表达作为第一个层次,也是构建强化学习算法的理论基础.在已知模型所 有参数的情况下,数学表达通常可以较为准确的推断出模型的结果,然而,数学上的合理性不意味着能被人所理 解;逻辑表达介于数学表达和感知表达之间,是对模型策略的近似,但逻辑表达方法产生的解释通常要求用户具 备特定领域的专业知识;感知表达对模型决策的重要因素进行筛选,并使用清晰、简洁的形式进行呈现,虽然结 果易于理解,但已经不具备重构策略的能力.总而言之,不同的解释在接近模型和接近人类感知之间存在着平 衡,难以兼顾.

3 强化学习可解释性的独有问题 

与其他 ML 方法不同,RL 问题由环境、任务、智能体三个关键因素组成.其中,环境为给定的具有一定内部规律的黑盒系统;任务为智能体为最大化其平均奖赏的而拟合的目标函数;策略是智能体行为的依据和一系 列行为之间的关联.根据强化学习的三个关键组成因素,本文归纳出 XRL 的三个独有问题,即环境解释,任务解 释,策略解释.三个独有问题之间存在着密切的关联,与整个强化学习过程密不可分,是实现强化学习解释直接 面临的问题.

4 强化学习可解释性研究现状 

由于 XRL 涉及的领域广泛,学者从各领域的角度出发,导致所提出的方法具有较大差异.因此,本节分两步 对相关方法进行总结.首先,根据技术类别和解释的展现形式,将现有方法分为视觉和语言辅助解释、策略模仿、 可解释模型、逻辑关系提取和策略分解五个类别.然后,在通用分类方法(即获取解释的时间、解释的范围)的基 础上,结合本文所提出的分类依据(即解释的程度,面对的关键科学问题),确定不同类别方法的属性.

在可解释性领域中,分类通常基于获取解释的时间和解释的范围两个因素[31] .具体而言,根据获取解释的 时间,可解释性方法被分为固有(intrinsic)解释和事后(post-hoc)解释.固有解释通过限制模型的表达,使模型在运 行时生成具备可解释性的输出.例如,基于较强可解释性的原理和组件(决策树、线性模型等)构造模型,或者通过 增加特定过程使模型生成可解释性的输出;事后解释是通过对模型行为的分析,总结模型的行为模式,从而达到 解释的目的.通常而言,固有解释是策略产生过程中的解释,特定于某个模型,而事后解释是策略产生后的解释, 与模型无关.根据解释的范围,可解释性方法被分为全局(global)解释和局部(local)解释,全局解释忽略模型的微 观结构(如参数、层数等因素),从宏观层面提供对模型的解释,局部解释从微观入手,通过分析模型的微观结构获 得对模型的解释.

除上述可解释性的通用分类之外,本文基于解释与模型和人类感知的符合程度,将可解释性方法分为数学 表达、逻辑表达和感知表达三类(见 2.4 ).这三类可解释性方法体现出可解释性算法在解释的形式、解释与模 型结果的近似程度和解释的直观度等方面的区别.前文(见 3 )分析了 XRL 面临的 3 个关键问题,即环境解释, 任务解释和策略解释.目前,单个 XRL 方法难以同时解决三类问题,因此,我们也以此为依据,对当前 XRL 方法所 着眼的问题进行区分. 

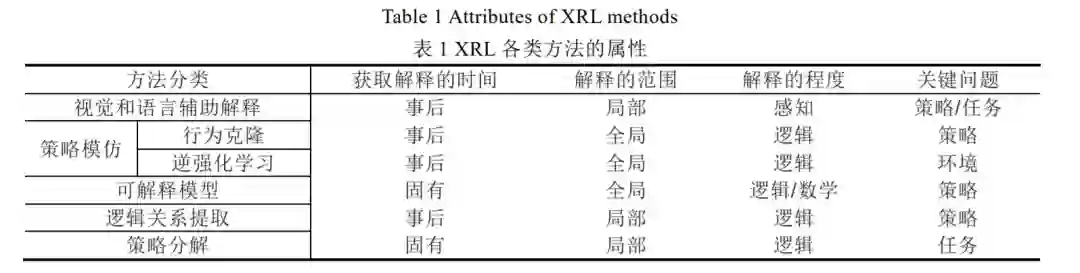
综上所述,本文以“获取解释的时间”、“解释的范围”、“解释的程度”以及“关键问题”为依据,对 XRL 方法 进行分类(见表 1).由于算法多样,表 1 仅显示大类别算法的特点,部分算法可能不完全符合

总结 

本文以 XRL 的问题为中心,讨论了该领域的基础问题,并对现有方法进行总结.由于目前在 XRL 领域,乃至 整个 XAI 领域尚未形成完整、统一的共识,导致不同研究的基础观点存在较大差异,难于类比.本文针对该领域 缺乏一致认知的问题,进行了较为深入的研究工作.首先,本文参考 XRL 领域的父问题——XAI,收集 XAI 领域 的现有观点,并整理出 XAI 领域较为通用的认识;其次,以 XAI 领域的定义为基础,讨论 XAI 与 XRL 面临的共同 问题;然后,结合强化学习自身的特点,提出 XRL 面临的独有问题;最后,总结了相关的研究方法,并对相关方法进 行分类.分类中包括作者明确指出为 XRL 的方法,也包括作者虽未着重强调,但实际对 XRL 有重要意义的方法. XRL 目前尚处于初步阶段,因此存在大量亟待解决的问题.本文重点提出环境和任务的解释、统一的评估标准 两类问题.本文认为这两类问题是为类 XRL 领域的基石,是值得重视的研究领域.

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“XRLS” 就可以获取《「强化学习可解释性」最新2022综述》专知下载链接

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源