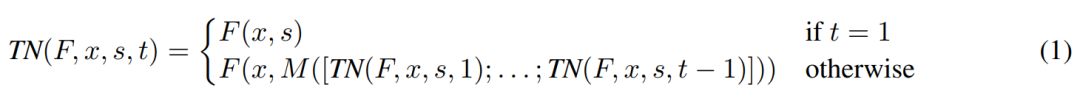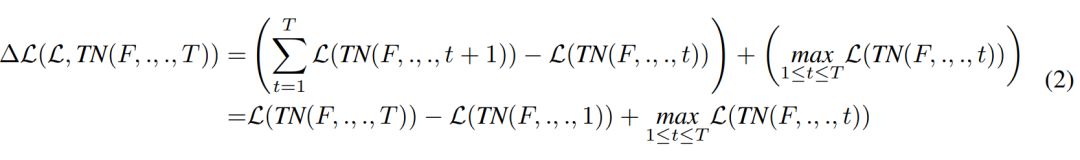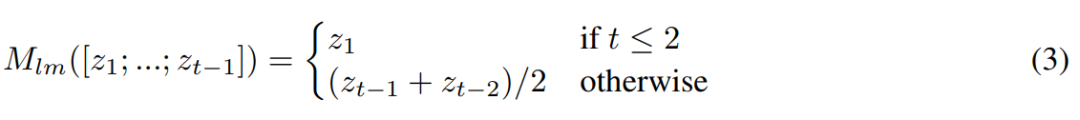ThinkNet:迄今为止最简单的语言建模网络
选自arXiv
作者:Jeffrey Dastin
机器之心编译
参与:陈韵莹、shooting
这篇短论文介绍了一种名为ThinkNet的模型。该模型非常简单,可以应用在语言建模任务中,且能在一些任务中达到当前最佳水平。
论文地址:https://arxiv.org/abs/1904.11816
这篇短论文介绍了一种名为Think Again Network(ThinkNet)的抽象概念,它可以用于任何状态依赖的函数(如循环神经网络)。本文中展示了该网络在语言建模任务中的简单应用,它在Penn Treebank上达到了当前最低的困惑度。
ThinkNet
给定任意的状态依赖函数F(x,s),其中x是输入,s是状态,ThinkNet可定义为:
其中s是一个初始状态,t ≥ 1是ThinkNet的时间步长,M([z1; ...; zt−1])是任意的混合函数(可以是静态函数或者是可训练的神经网络),该混合函数将之前所有的输出组合成一个新的状态。然后优化函数 L(TN(F, ., ., T )),而不是损失函数L(F(., .))。
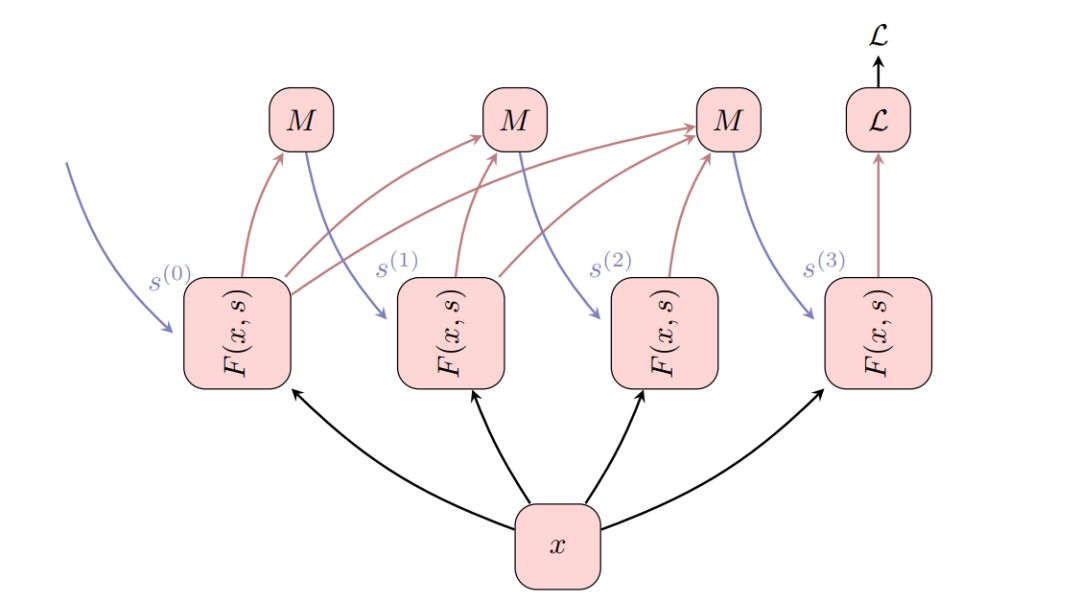
图1:运行4个时间步长的ThinkNet示意图(在状态依赖函数F(x, s)上实现)。在t=0时,网络以状态s(0)进行初始化。在 t > 0时,混合函数M根据之前的时间步长t、t-1、……、1生成的所有输出来计算下一个状态s(t+1)。最终,在流程的最后计算损失L。
实质上,“Think Again”抽象概念通过添加额外的循环来扩展任何状态依赖函数。其理念是将函数F(x, s)重复运行t次(每次运行对应一个ThinkNet时间步长),并让混合函数M为下一次执行准备初始状态。
为此,可将M定义为该网络之前生成的所有输出的函数。“Think Again”的概念暗指一个人通过多次行动来完成任务:在其已经处理了手头问题并更新了“思维状态”之后,再次思考该问题通常是很有用的。
概念上,任何问题都可以通过这个框架来解决,正如:人们在再次解决问题时会学会对以前所有的答案(z1, z2, . . . , zt−1)进行推理(为此,我们训练了自己的“混合函数”M)。
从人类问题解决者和深度学习模型的角度来看,这都是有意义的,这可以得益于在处理问题时提前了解了问题的内在表现。在语言/序列建模的环境中,如果我们在阅读短语/序列时预先知道它将如何结束,则将从中受益。
Delta Loss
定义ThinkNet后,我们可以在T个时间步长后简单地计算其损失。我们提出了另一种选择,Delta Loss (∆L):
等式 2 的第一项是在时间步长t和t+1时后续损失之间所有差异的和。对此项进行梯度下降会促使模型最大化在每个时间步长降低损失的速率。与其促使模型在T次迭代后产生令人满意的损失,我们鼓励其在每个时间步长改善其解决方案。
我们的假设这将促进收敛:以Delta Loss训练的模型应该可以将其计算扩展到更多的时间步长并产生更好的结果。相比之下,只用最后的损失L(TN(F, ., ., T ))训练的模型,可能只得到较差的中间状态,如果超过t个时间步长后使用它们,则反过来会导致发散。
等式 2中的“差异和”项有一个有趣的属性,它是可伸缩的,除了第一项和最后一项,其它项都可相互抵消,结果变成L(TN(F, ., ., T )) − L(TN(F, ., ., 1))。这使得整个方程简单多了,虽然效率不高——因为仍然需要迭代所有损失来计算最大损失项。
自然地,该模型可以自由地学习操纵其输入以便在某个时刻生成很高的损失,以减少它并得到一个很大的delta。这可以通过将所有迭代中的最大损失作为等式 2的附加项来防止。
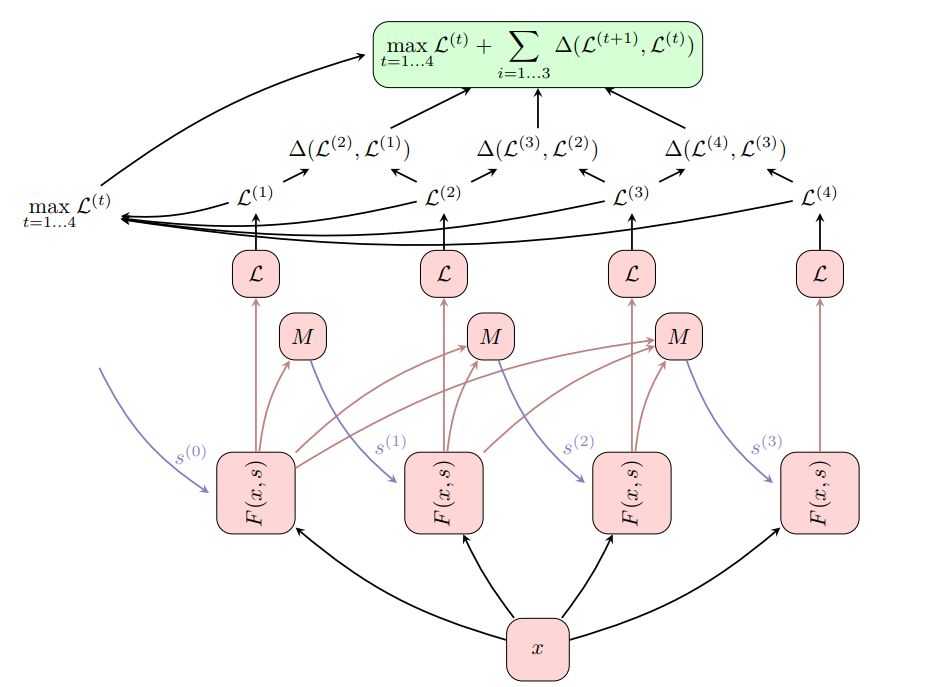
图2:用Delta Loss扩充的ThinkNet。其基础架构与图1中所示的相同,但是这里我们在每个ThinkNet时间步长t上计算了损失L(t)。计算后续损失之间的Delta∆(L (t+1) ,L (t) ),然后最终的损失被定义为所有时间步长的最大损失maxL(t)加上所有delta P∆(L (t+1) ,L (t) )。
语言建模中的应用
给定一系列token,语言模型给出下一个可能出现的token的概率分布或者Plm(xt|x1, . . . , xt−1)。当使用神经网络(如LSTM[10])对P建模时,会获得非常好的结果。在这里,我们将AWD-LSTM[11]语言模型封装在ThinkNet中并评估其性能。
AWD-LSTM 的编码器 Flm(x, s)在观察到具有一些先前状态s的一系列token x后会给出序列表征。将 Flm 转换为 ThinkNet 所需的只是一个混合函数。下面我们选择简单的函数:
这里求前两个状态的平均值,其中zt = [(h1, c1); ...; (hL; cL)],并且每个元组和 (hl , cl)上的求和与除法都是以元素为单位计算的。
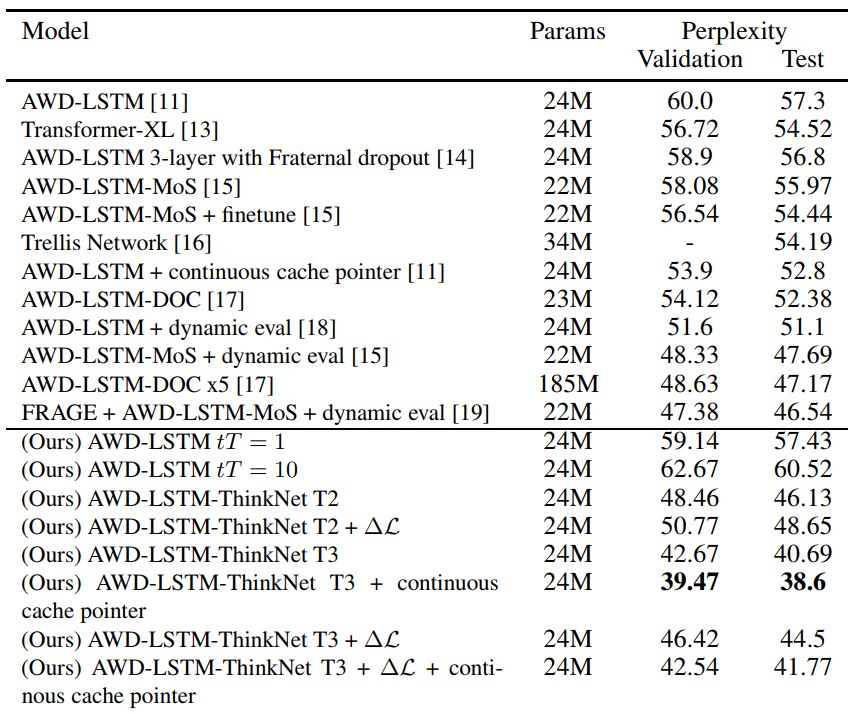
我们在表1中的结果表明,有10个测试ThinkNet时间步长训练的ThinkNet T3模型即使没有连续的缓存指针(cache pointer)也能实现目前最好的性能。如果使用连续缓存指针,差距更大。我们还认为它是迄今为止此类模型中最简单的模型。另外值得注意的是,我们没有进行任何超参数调优。
表1:上面是PTB语言建模的先前最佳技术,下面是我们的模型。所有ThinkNet模型都使用tT = 10(测试ThinkNet时间步长)。在没有使用原始AWDLSTM模型任何附加参数的情况下,以3个时间步长训练的两个ThinkNet模型都大大超过了先前的技术水平。
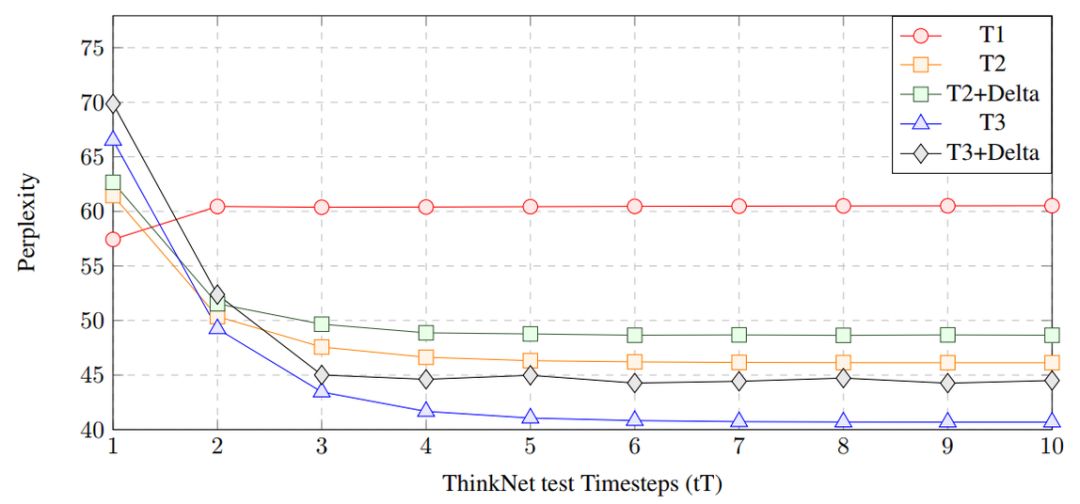
图3:在PTB上,以1到3 个ThinkNet 时间步长训练的模型在1到10个测试时间步长 (tT)下进行评估。然而普通的AWD-LSTM 模型 (T1) 的性能在超过训练使用的时间步长时会下降,但ThinkNet模型会继续改进直到收敛。
本文为机器之心编译,转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心(全职记者 / 实习生):hr@jiqizhixin.com
投稿或寻求报道:content@jiqizhixin.com
广告 & 商务合作:bd@jiqizhixin.com