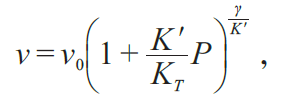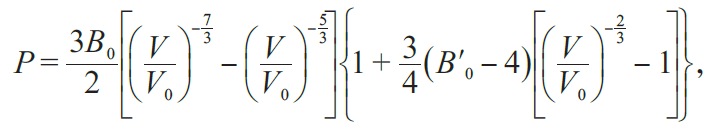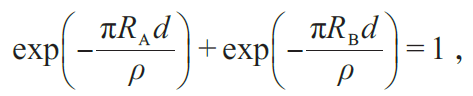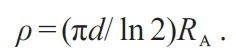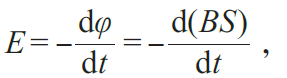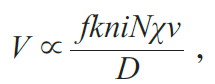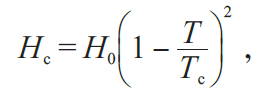原位高压测试技术在高压结构及性质研究中的应用
作者:黄艳萍 黄晓丽 崔田 (吉林大学物理学院超硬材料国家重点实验室)

摘要 高压科学是研究不同压力条件下物质的结构、状态、理化性质及变化规律的学科。在高压科学研究中,多以凝聚态物质为研究对象,涉及的领域也非常广泛,包括物理学、化学、材料学、地质学、生物学、航天学等等,是一门以实验为基础的学科。高压科学之所以能成为一门独立的学科,还因为高压研究需要使用特殊且精巧的技术和方法来实现,是以技术创新为牵引的科学研究领域。而今,各种实验测试手段已经可以成熟地运用在该学科中,比较常见的有:高压拉曼散射、高压红外光谱、高压布里渊散射、高压同步辐射XRD、高压电学测量以及高压磁学测量等诸多技术。文章系统介绍了以上高压原位实验测试方法的原理、发展、作用及应用,有助于读者对原位高压测试技术有更深刻的认识和理解,为更高压力下的原位高压探测技术的发展提供重要的基础和借鉴作用。
关键词 高压拉曼,高压红外,高压布里渊,高压同步辐射,高压电学,高压磁学
与温度、化学组分类似,压力(强)对我们而言并不陌生,也是一个非常重要的热力学因素[1—6],对物质的结构和性质有着重要的影响作用。所谓高压是泛指一切高于常压条件的压力环境。物质在压力的作用下,其体积以至原子间距都会发生收缩,内部能量状态发生变化,从而引起物质性质的改变。当压力达到一定程度后,物质就会出现结构转变,比如从气态到液态的转变,从液态到固态的转变,一种晶体结构到另一种晶体结构的转变,以及绝缘态到金属态的转变,也就是我们常说的压致相变。高压科学是研究物质在不同压力下的结构、状态、理化性质及变化规律的学科,是一门以实验为基础的学科。
高压实验技术是进行高压极端条件下材料物性研究必不可少的手段,需要使用特殊且精巧的方法来实现,涉及凝聚态物理学、化学、材料学、生物学、地质学等领域,并且已经取得了许多重要的研究成果。最早的高压科学研究是在18世纪中期慢慢发展起来的,J. 坎顿对水的压缩性进行了实验研究。随后,阿马伽(Amagat)在19 世纪末发明了活塞压力计。对高压相变的研究起源于塔曼利(Tammann)测量了物质的体积在压力变化时出现的不连续现象。这些工作都属于高压物理研究的初始阶段。发展到20 世纪50 年代以后,高压物理科学有了重大突破,德里卡莫通过固体的电子谱、稀土盐类光谱、有机化合物的电子谱等测试手段将高压研究推向了一个新的高潮[7—10]。
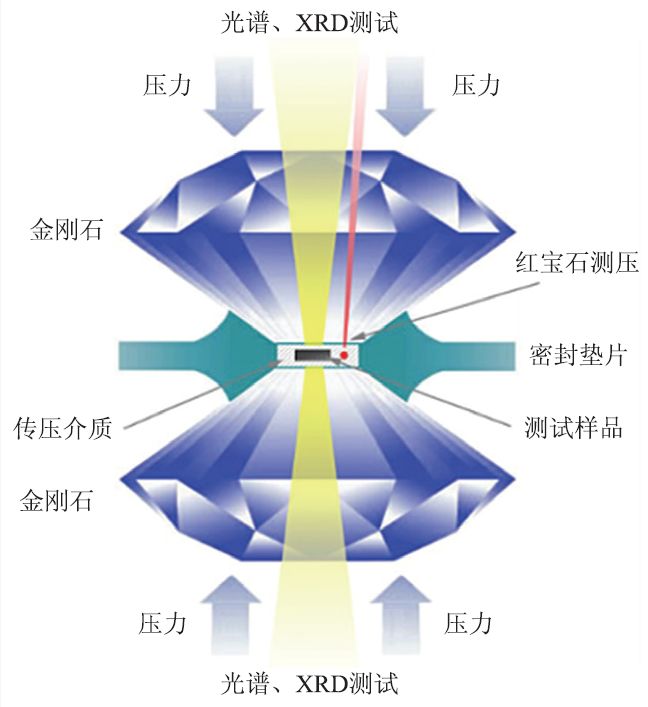
金刚石对顶砧(DAC)作为探索物质在高压下物性变化的有利工具,其中一个重要的原因是金刚石具有良好的光透过性,适合做高压腔体的测量窗口。它不仅可以通过光学显微镜观察样品在压力下的形貌变化,还可以进行多种光谱学测量研究,包括高压拉曼散射、高压红外光谱、高压布里渊散射、高压同步辐射X光衍射等等。金刚石对顶砧的基本工作原理非常简单易懂。如图1所示,将两颗金刚石平行放置,中间用带有小孔的封垫物质隔开,将样品放在小孔中,通过对上下两颗金刚石施加压力,使得样品腔中的样品在很小的空间内可以产生较大的压力。另外,高压实验研究使人们认识到常压低温下为非超导的物质在高压低温下具有超导性,例如,除了已知的23 种元素的单质在常压低温下具有超导性质外,还发现有29 种元素的单质在高压下具有超导性质。除单质外,很多化合物在高压低温下也具有超导性质,H3S 是迄今为止实验上发现超导转变温度最高的化合物[11,12]。一种物质具有超导特性最直接的表现有两个:零电阻现象和迈森纳效应。因而,高压电学测量以及高压磁学测量技术也是高压科学中必不可少的研究手段。
图1 金刚石对顶砧装置基本工作原理示意图
本文将系统地介绍原位高压实验技术的原理、发展、作用及应用。主要包括:高压拉曼光谱、高压红外光谱、高压布里渊光谱、高压同步辐射X光衍射、高压电学测量以及高压磁学测量。
与其他分析仪器相比较,拉曼光谱技术应用于高压实验研究是最方便快捷的手段之一。因激发光源为可见光,所以拉曼光谱方法可以很容易地直接应用到金刚石对顶砧压腔的原位高压实验测量。
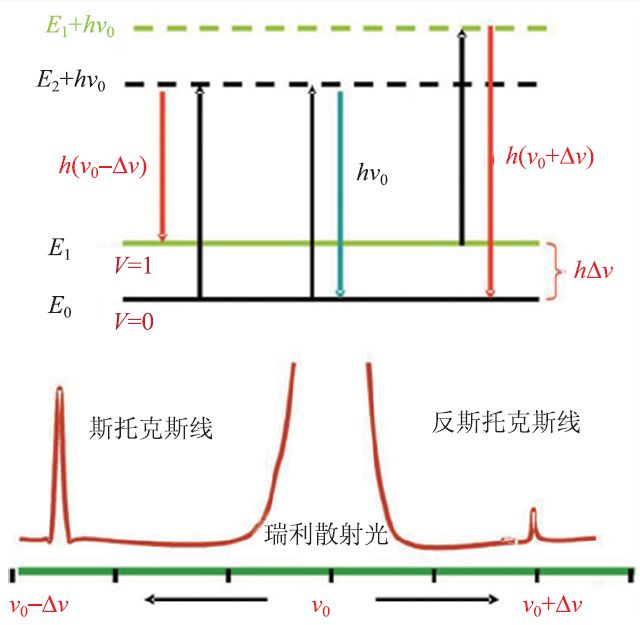
拉曼散射的本质是非弹性散射。当一束频率为ν0的单色光作用于物质时,除了存在与入射光相同频率的瑞利散射光(ν0)外,还产生了新的不同频率的散射光,比入射光频率小的(ν0-Δν),称为斯托克斯线;比入射光频率大的(ν0+Δν),被称之为反斯托克斯线。相应地,这3 种出射光的能量分别为hν0、h(ν0-Δν)和h(ν0+Δν)。其中,Δν被称为拉曼频移。即当一束光照射到分子上时,出射光的能量发生改变的现象,叫做拉曼散射。图2给出了拉曼散射的基本原理示意图。
图2 拉曼光谱的基本原理
最早的高压拉曼实验可以追溯到1968 年,Brasch 等人首次在金刚石对顶砧装置上采用零度散射方法进行了原位高压拉曼光谱研究[13]。1973年,Adums 等人首次采用背散射方法进行拉曼光谱研究[14]。近些年,随着拉曼光谱技术与高压实验技术的迅速发展,拉曼光谱在高压原位测量上有着举足轻重的地位。高压拉曼光谱作为一种振动光谱技术,其频率可以覆盖分子振动的所有区间,可以进行高压下固体、液体等物质的物相分析以及物质微观结构的测定和相变等研究。
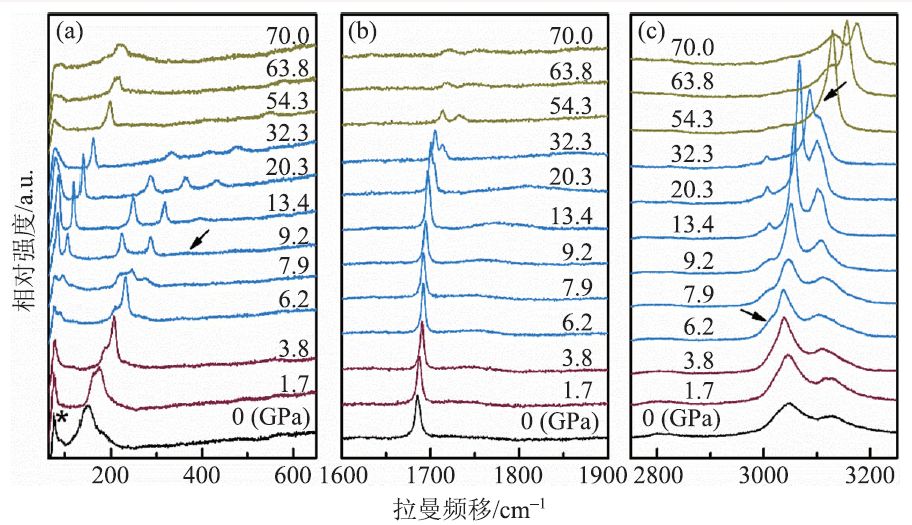
除少数离子键性强的物质外,一般的气相、液相和固相物质大都具有拉曼散射信号。拉曼散射光谱有几个重要的参数:拉曼频移(Δν)、拉曼散射强度(I)和拉曼峰半高宽(FWHM),相应地,从高压拉曼散射光谱可以得到的基本参数是:拉曼频移随压力的变化情况、拉曼散射强度随压力的变化情况以及拉曼峰半高宽随压力的变化情况。拉曼频移随压力的变化情况包含着键强度和原子质点之间的间距以及它们之间的相互作用随压力的变化情况。如样品的拉曼频移随压力的斜率dν/dP 值越大,表明单位压强对特定质点之间振动的影响越大,即该特定质点之间的键强度越小。拉曼散射峰的强度可以作为物质定量分析的基础。综合以上信息,可以从高压拉曼光谱中得到物质的相变信息。图3 是溴化铵(NH4Br)在不同压力下的拉曼光谱图。从图中可以看到,NH4Br 在高压下的不同态可以明显从其拉曼峰的形状和位置加以区分,其中,NH4Br 无序相的稳定压力范围为0—1.7 GPa,NH4Br-IV 有序相的压力范围为1.7—3.8 GPa,NH4Br-V 相的压力范围为6.2—32.3 GPa,NH4Br-VI 相的压力范围为54.3—70 GPa[15]。
图3 NH4Br 的拉曼振动峰随压力的变化情况[15]
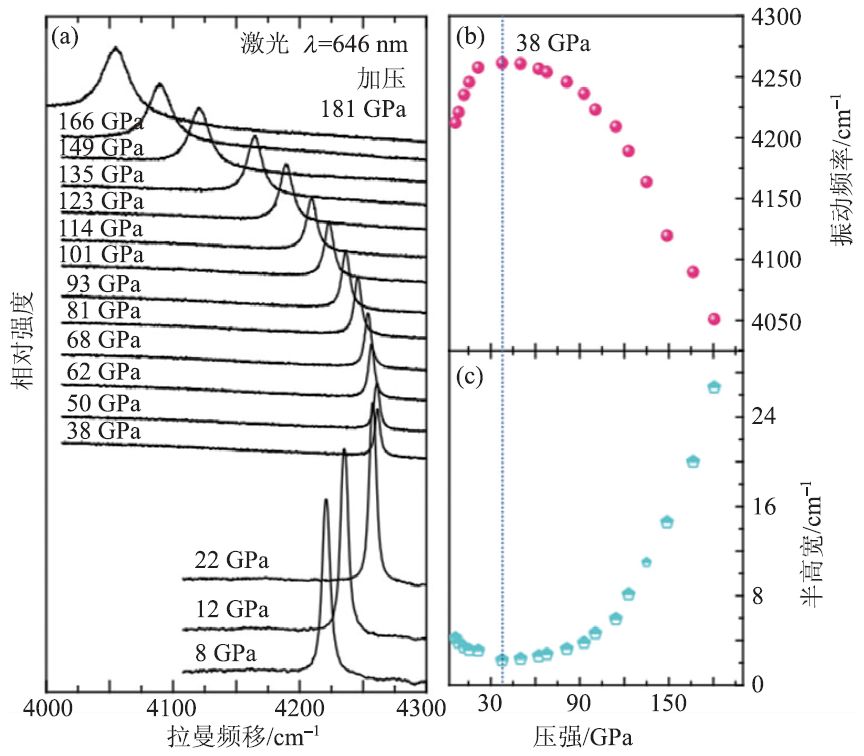
在许多情况下,仅从拉曼光谱图上进行相变的识别并不容易,而需要从多方面进行分析,这包括拉曼光谱图中所有峰的位置及其半高宽与压力之间的关系(拉曼参数对压力和温度的斜率dν/dP、dν/dT 等)。图4 为纯氢的H-H 键的伸缩振动峰[16],从图中可以看出,根据拉曼频移和半高宽随压力的变化,可以分析得出从8 到38 GPa,随压力增加,氢原子间距变小,振动频率增加,拉曼峰蓝移;从38 到181 GPa,由于分子内共价键变弱,分子间的作用力增强,从而导致振动频率减小并且振动逐渐展宽。
图4 在压力范围8—181 GPa纯氢的H-H键的伸缩振动峰[16]
若将高压拉曼与高温手段结合,还能得到样品的弹性信息。类似于Murnaghan状态方程,晶格振动的拉曼频移与弹性参数之间的关系可以表示为
式中,ν是压力P 下的拉曼频移(cm-1);ν0是零压下的拉曼频移(cm-1);KT (GPa)和K'分别是等温体变量及其对压力的导数;γ是模式Gruneisen 参数。若已知K'、KT和γ 值中的任何一个值便可以获得其他两个弹性参数值。
当一束波长不同的红外射线照射到物质上时,物质分子的晶格振动会选择吸收特定波长的射线,引起分子由低能态到高能态的过渡,即能级的跃迁,形成该物质分子晶格振动的红外吸收光谱,简称红外光谱[17]。由于不同分子的组成与结构不同,因此不同物质对应的红外吸收光谱也不同,所以可以通过测量分子的红外吸收光谱来分析与鉴定分子的结构。红外光谱在可见光区至微波光区之间,按照波长范围可以分为近红外光区(0.75—2.5 μm)、中红外光区(2.5—25 μm) 和远红外光区(25—1000 μm)3 个区段,其中,中红外光区是研究和应用最多的光谱区域。
红外光谱技术的研究发展至今已经历了上百年的历史,19 世纪末,Julius 通过岩盐棱镜和电阻温度计第一次探测到了红外吸收光谱,发现含甲基的分子在2900 cm-1处都有一个吸收光谱。随后越来越多的学者开始了对红外吸收光谱的研究,发现有机化合物的结构与其红外吸收光谱有关。1905 年,Coblentz 得到了128 种有机与无机化合物的光谱,由此得出了分子结构与红外吸收光谱的关系[18]。在随后的几十年里,相继诞生了三代红外光谱仪——棱镜型、光栅型和傅里叶变换型。在高压科学研究领域里,高级商品化的傅里叶红外光谱仪的探测器基本可以满足金刚石压腔红外光谱测量的灵敏度要求。
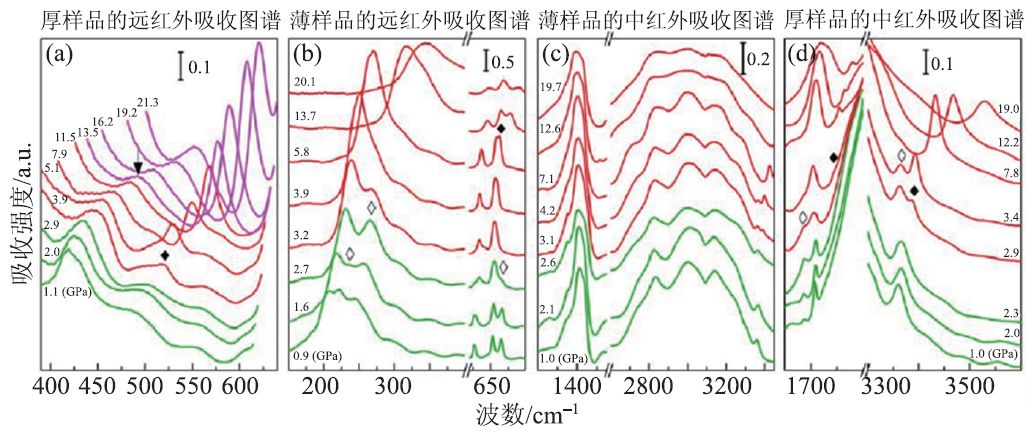
红外光谱与拉曼光谱均属于分子振动能级的光谱,目前技术上多采用中红外吸收光谱(简称红外光谱),是拉曼光谱技术的互补手段,它们的研究方法也很类似。例如,2014 年,Wu[19]等人在室温条件下,利用DAC超高压实验技术,结合高压XRD光谱、高压Raman光谱以及原位高压红外吸收光谱,对NH4N3进行了高压结构相变以及结构稳定性的研究。高压红外吸收光谱实验的最高压力为20 GPa,如图5 所示。发现在0—2.9 GPa过程中晶胞参数a、c 趋近相同,得到NH4N3 在2.9 GPa发生了正交结构→四方结构的二级结构相变。NH4N3 在高压相中始终以叠氮根离子和铵根离子形式存在且仍以氢键连接;还确定了氢键的键能在0—2.9 GPa 内减弱、在2.9—12 GPa 内增强且在12—20 GPa 内再次减弱。在2.9 GPa 处的变化是由结构相变引起的,在12 GPa 处的变化是由叠氮根离子的旋转或弯折引起的,不伴随结构相变的发生。
图5 0—20 GPa时NH4N3的高压远红外和中红外吸收光谱[19]
高温高压下物质的声学性质研究可以提供物质的弹性参数,如体变模量、剪切模量、泊松比等许多重要的信息。尤其是当所研究的物质为非晶态物质,如熔体或者玻璃时,X射线衍射方法已经不能获得样品的体积参数,采用声学性质的测试也许是获得非晶态或液体物质体积和弹性参数的唯一选择。目前,涉及高压声学测量最常用的手段就是高压布里渊散射。
布里渊散射是由声学振动引起的非弹性散射。其产生的原因与拉曼散射类似,不同的是,布里渊散射引起的非弹性散射含有声学振动的信息,其引起的位移能量在声学能量范围内,远低于拉曼散射的位移能量。布里渊散射作为一种纯光学的测量手段,可以将其与金刚石对顶砧高压技术结合在一起。布里渊散射可以对非常小的样品(几十微米)进行测量,所以可以利用金刚石对顶砧来进行超高压的研究。
图6 金刚石压砧中最常用的布里渊散射几何配置
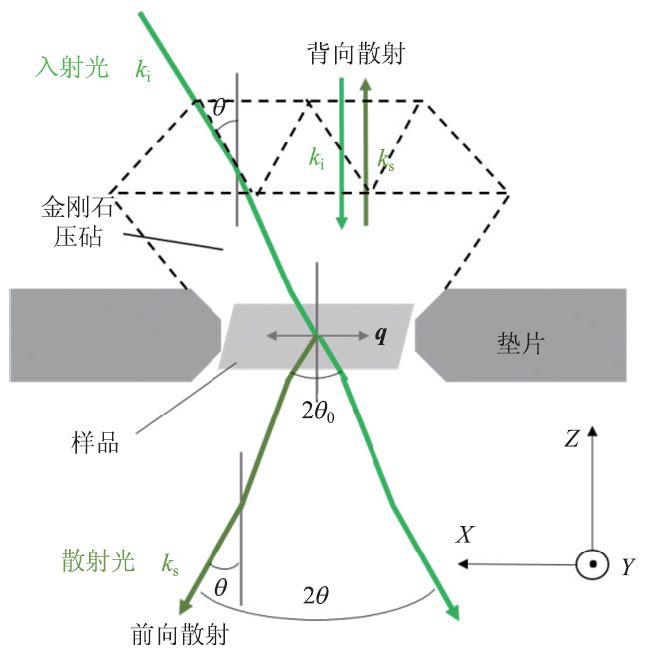
在金刚石压砧中最常用的布里渊散射几何配置如图6所示。
如图所示,对于背向散射来说,样品平面内的声子的波矢q 与入射光ki和散射光ks的关系是:|q| = 2nk ;对前向散射来说,经由金刚石折射后,关系式变为:|q| = 2nk sin θ0 = 2k sin θ ,其中n 为样品折射率。在前向散射中,入射光和样品的夹角与散射角相等,根据斯涅耳定律,不需要知道样品的折射率就可以计算出声速,即当声速已知时,结合背向散射的频移结果就可以推导出折射率。前向散射中折射率不参与计算,所以前向布里渊散射的应用相对也比较广泛。
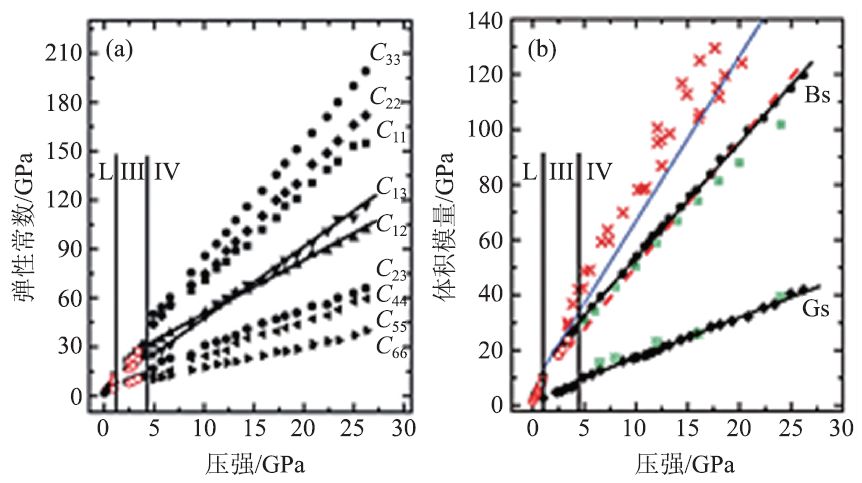
1976 年,Whitfield 等[20]首次在金刚石压腔中进行了布里渊散射测量,早期使用的压机及托块要按照不同的散射角度来钻孔,但这种情况下最高压力不是很高,同时,对于晶体取向不确定的样品也无法计算弹性常数。1992 年,Shimizu 和Sasaki[21]发明了一种新的实验方法,通过旋转金刚石压机来测量平行金刚石砧面的任何方向的声子布里渊散射,之后通过拟合Christoffel 方程,得到弹性常数。几十年间,高压布里渊散射实验技术取得了飞速发展,2009 年,Murakami[22]将MgO的高压布里渊散射研究的压力提升至130 GPa。通过对布里渊散射频移的测定,可以精确地计算出高压下物质的声速、折射率、弹性系数、弹光系数、状态方程等一些基本的物理量。2011 年,Li 等[23]人结合高压布里渊和拉曼散射技术,成功获得单晶NH3液态、立方相III 和正交相IV的弹性常数和体积模量随压力的变化,发现C12和C13在12 GPa 发生交叉,C表示弹性常数,随着压力的变化情况可以反映出材料的结构相变,同时观察到拉曼光谱弯曲振动发生变化,推测在12 GPa发生结构变化,如图7所示。
图7 NH3弹性常数和体积模量随压力变化
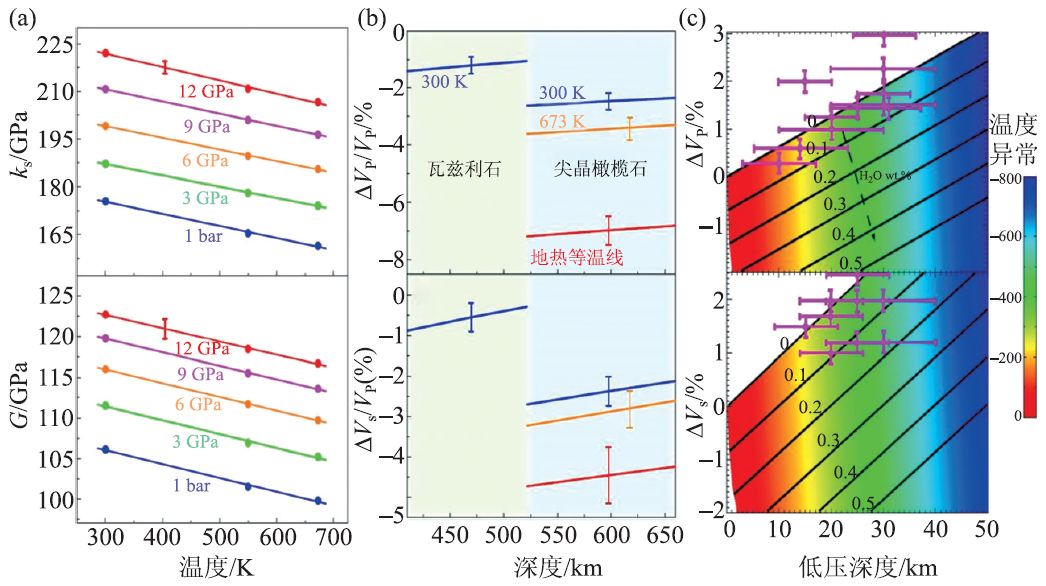
布里渊散射的一个重要用途是测定电介质晶体弹性系数张量的分量。当晶体发生相变时其弹性通常表现异常,因此可以利用布里渊技术来探测物质的高压相变并为原子间相互作用力提供信息。高温高压下弹性系数的测量是获得地球内部矿物的切变性质的唯一方法,故高温高压布里渊散射的研究对于构建出地球内部物质的矿物学模型亦是非常重要的[24]。2012 年,Mao 等[25]通过对含水林伍德石的弹性性质随压力和温度的变化情况的研究,解释了水合作用对地幔主要矿物声速的影响并估量地幔的水含量,如图8 所示,同时提出地震波速异常和660 km间断面的位置下移可能是由水的热力学作用引起。2006 年,Li 等[26]利用激光加热高温高压布里渊散射技术,首次发现了水存在由低密度向高密度相转变的液—液相转变边界,探讨了高温高压对液态水声速、弹性和分子结构的影响,解决了存在已久的争议问题,拓展了水的高温高压相图。目前,布里渊散射结合激光加热和黑体辐射技术,温度可以达到2500 K[27]。
图8 (a) 含水林伍德石的弹性性质随着压力和温度的变化情况;(b)水合作用对分布在地幔的林伍德石声速的影响;(c)过渡区底部的水和温度异常(660 km深度)[25]
将布里渊散射的实验结果与拉曼散射、中子非弹性散射以及X射线衍射测量结果结合起来,更有助于对固体相变行为的了解。对高温高压布里渊散射的研究,不仅可以提供物质在极端条件下的基本结构信息,还可以获得物质在高温高压下的声速以及弹性性质的数据。布里渊散射在材料性质的研究中应用非常广泛。布里渊散射可提供透明、不透明的晶体,半导体及金属和它们的超晶格材料, 铁( 介)电,超导和氧化物的磁性及弹性参数的测量;利用布里渊散射可研究有机溶液的液—气相变。布里渊散射还可作为海洋遥感探测手段监测水下目标。
结晶物质的X射线衍射分析可以获得晶体中的面间距和晶胞参数,由此可以获得物质的体积参数。根据不同温度和压力下的体积数据可以研究物质的弹性和状态方程等重要的物理参数。另外,X射线分析也是进行物质相态鉴定的最好方法之一。在高压科学领域里,尤其是金刚石对顶砧装置来说,它的样品腔很小,若用普通的X光机进行探测,在强度、发散度和测量时间上都会对研究工作产生极大阻碍。此时,同步辐射光源的出现,完美地解决了这些问题。同步辐射光是一种多波长的X射线,其产生原理是:当速度接近于光速的带电粒子在磁场做圆周运动时,会沿着偏转轨道的切线方向发射连续谱的X 射线。1947 年人类在电子同步加速器上首次观测到了这种电磁波,并称其为同步辐射或同步辐射光。目前,世界上已有近40 台同步辐射光源正在运行,在中国可以进行高压同步辐射研究的有北京同步辐射装置和上海同步辐射光源。
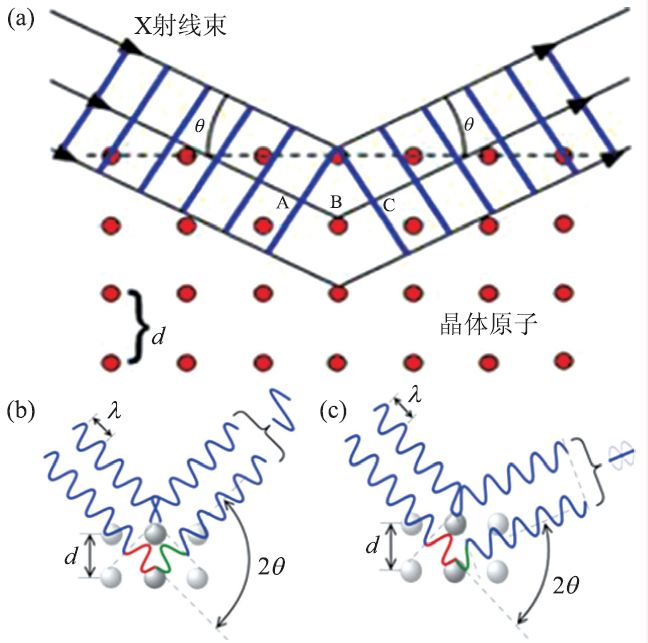
X射线衍射的核心是布拉格定律:当一束单色X射线入射到由原子排列规则的晶体时,如图9 所示,晶体中获得X射线能量的各原子便发射X射线而产生干涉,从而在某些特定方向上产生加强的X射线,其在空间分布的方位符合布拉格定律:λ=2dsinθ。其中,d 为晶面间距,θ为入射X光与晶面间夹角,λ为入射X光的波长。
图9 布拉格定律示意图
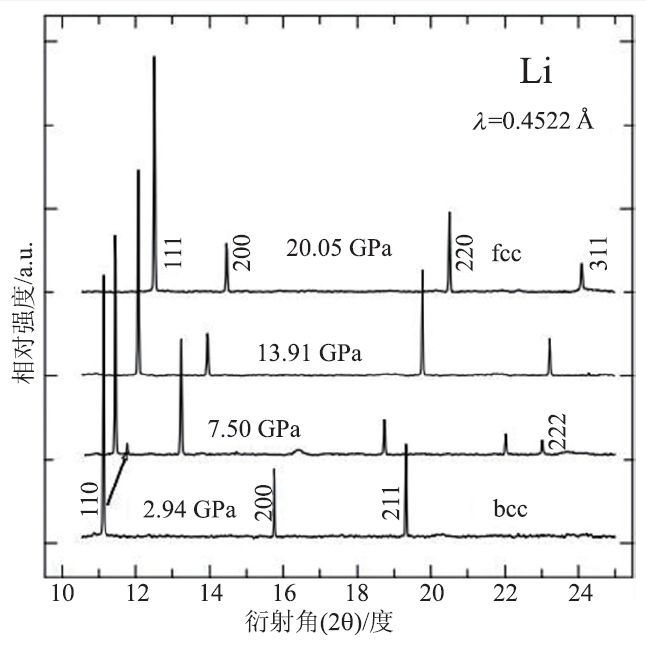
在高压科学实验研究中,通过X射线分析可以获得物质的弹性参数、状态方程以及相变的信息。物质发生相变的一个最重要变化是它们的结构发生了转变,这种变化会直接反映在其X射线衍射图谱上数量及角度的变化。图10 是单质Li 的高压同步辐射XRD 图谱,其中可以很清楚地看出,当压力达到7.5 GPa 时,单质Li 的结构从原来的bcc相转变成了fcc相。
图10 单质Li的X射线衍射图谱随压力的变化情况[28]
高压同步辐射XRD图谱还可以给出晶态物质的晶胞参数,进而得出物质的体积随压力的变化情况,还可以将体积随压力的变化曲线与以下三阶Birch—Murnaghan 方程进行拟合[29],可以得到物质的体变模量弹性参数:
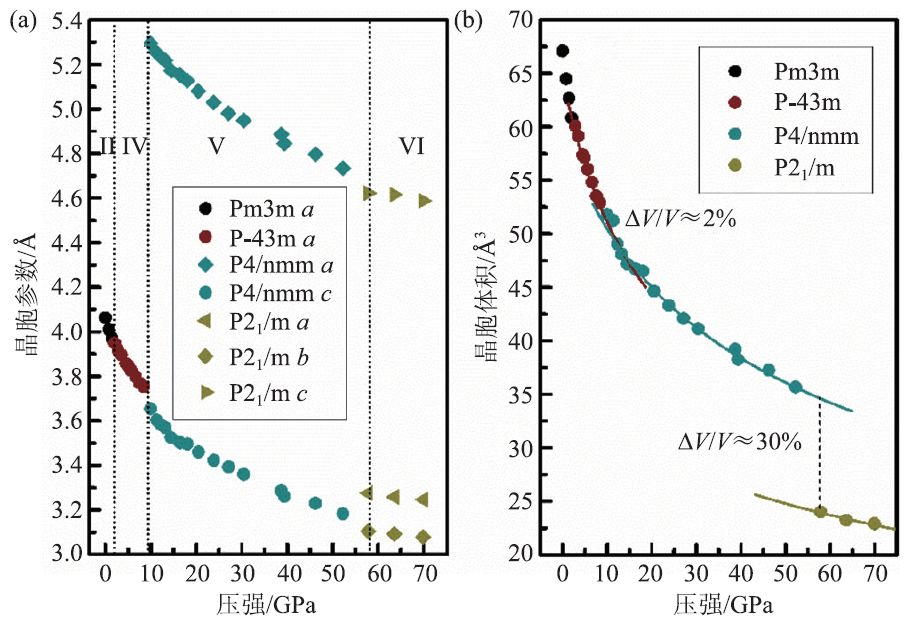
在此方程中,V0是常压时晶胞内每个分子的体积,V 是任意压力下晶胞内每个分子的体积,B0是晶体的体弹模量,B0′是体弹模量对压力的一阶导数。图11 给出了NH4Br 各个相的晶胞参数以及体积随压力的变化趋势。对于NH4Br 的各个相来说,晶胞参数的变化几乎都是各向同性的。从图11(b)中可以看出,相IV 到相V的转变伴随着2%的体积塌缩,而相V到相VI 的转变则伴随着30%的体积塌缩。
图11 (a)NH4Br晶胞参数随压力的变化情况及(b)各相中每个分子的体积随压力的变化[15]
物质的结构相变会影响材料载流子的产生以及散射效应的改变,反映在电学性质上,相应的电学参数也会发生改变。另一方面,超导电性的研究一直是凝聚态物理中的热门研究方向,寻找高温超导体已然成为物理学和材料学的重点课题之一。零电阻现象是超导体具有的基本特征之一,并且是超导体最直接的证据,因此,测量样品的电学性质对于超导体的研究也有着至关重要的作用。
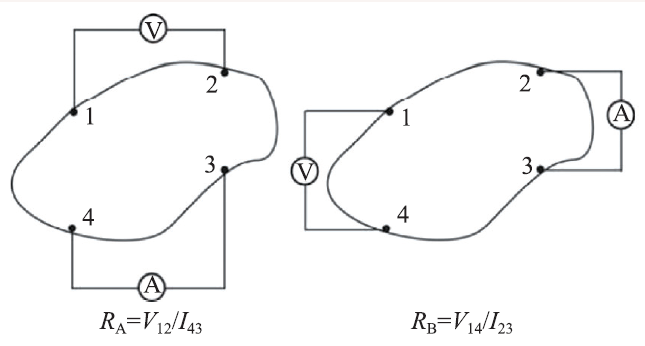
从电极布局上看,金刚石压腔中样品的电阻测量最常用的方法是范德堡法。范德堡法测电阻率适用于任何形状不规则、等厚、材质均匀的材料,对于电极和样品的接触面积要求尽量小。如图12 所示,样品的边缘有4 个电极,电流I43从触点4 流入,触点3 流出,在触点1、2 之间测得电压值是V12, 可得RA=V12/I43, 同理,可得RB=V14/I23。样品的电阻率由以下公式得到:
其中,ρ是样品的电阻率,d 是样品的厚度。而对于高压下的样品,我们认为样品是中心对称的,电阻率则可以表示为:
图12 Van der Pauw法测量电阻率工作原理[30]
目前,DAC上的高压电学测量的电极布置主要有两种方法:手工布线和集成电极技术。
手工布线采用极细的金属丝作为电极,将电极布置在样品腔中,使得每根电极和样品接触的面积尽量相同。同时,电极和垫片之间要做好绝缘。我们采用立方氮化硼作为绝缘物质,具体步骤如下:首先,用金刚石对顶砧将垫片预压到实验所需的厚度,利用激光打孔或者电火花打孔在预压好的垫片上制备出样品腔。其次,绝缘粉的制备也极其关键,我们将立方氮化硼和环氧树脂按照10 :1 的比例混合,研磨,在一定温度下烘干之后作为绝缘物质。之后将适量的绝缘粉填入样品腔和压痕中,利用金刚石对顶砧将绝缘粉压至致密状态,注意绝缘粉不能过少,过少起不到绝缘的作用,同时绝缘粉也不能过多,过多容易使得绝缘粉不致密,影响实验效果。并且要保证预压的垫片和压痕侧壁都有绝缘粉,以起到充分的绝缘效果。最后,在带有绝缘粉的垫片上制备出适合实验的样品腔,此时样品腔的大小应该略小于第一次制备的样品腔。手工布线对操作者的技术要求极高,需要经过严格的培训和经验积累。图13是手工布电极的样品腔示意图。
图13 手工布电极的样品腔示意图
金刚石压砧上集成薄膜微电路的程序如下:①采用磁控溅射的方法在金刚石砧面上制备一层绝热的氧化铝薄膜;②在氧化铝表面制备一层厚约3 μm的金属钼;③采用光刻的方法将薄膜制备成所需的电极;④在电极上制备一层氧化铝绝缘保护层:⑤刻蚀探测窗电极接触端;⑥粘电极引出线。之所以大多数薄膜微电路选用钼作为电极的材料,主要是因为:钼金属有大的体变模量(230 GPa)和硬度,其相变压力高达210 GPa,并且钼易于进行光刻加工。
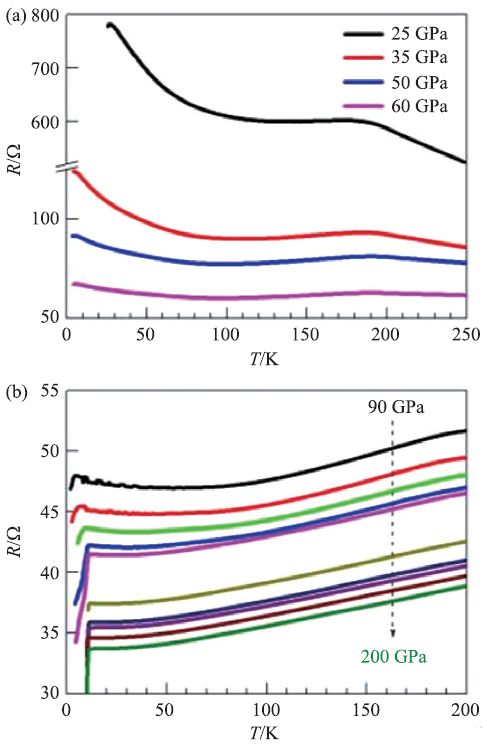
近些年来,高压电学测量已经取得了一系列重要的成果。2017 年,Zhenhua Chi 等人对层状材料MoS2进行了高压电学实验研究,发现当压力达到90 GPa 时,MoS2由原来的半导体转变成超导态,在整个研究的压力区间内,超导转变温度最高达11.5 K[31],如图14所示。
图14 MoS2的电阻随压力的变化情况[31]
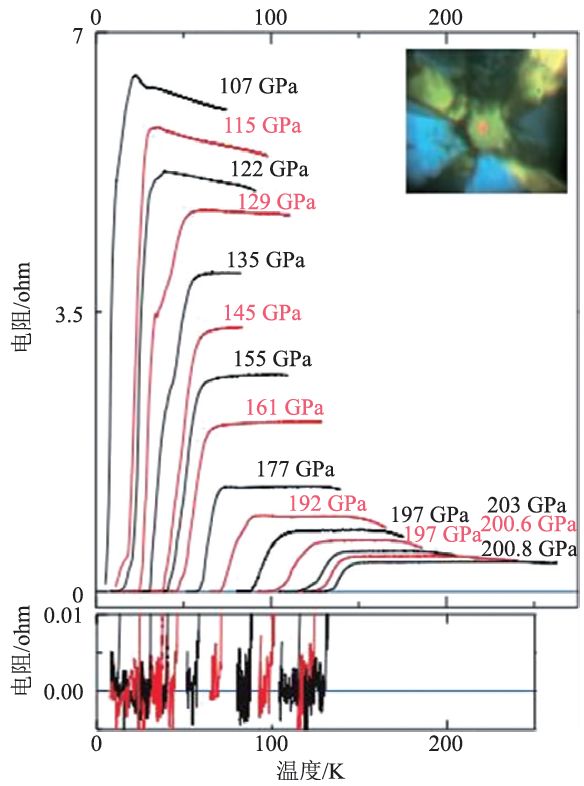
2015 年,Eremets 等人又通过测量H2S在高压下的电阻发现了历史上超导转变温度最高的材料,在158 万大气压,其Tc=203 K[12],如图15 所示。这一发现使得越来越多的人希望通过测量高压下的电阻来发掘更多的高温超导材料。
图15 H2S的电阻随压力的变化情况[12]
物质的磁性是物理学中重要的研究领域。高压下物质的磁矩会发生变化,并造成磁性质的变化和新现象的出现,因此高压磁性质的研究可以为许多领域的研究提供重要信息。
对于高压下物质的磁性测量主要是利用感应线圈对磁化样品的磁通量的变化进行测量,根据磁通量发生变化的途径又分为交流磁性测量和直流磁性测量。目前,对高压下样品的磁性进行测量主要是交流互感法。互感法是在金刚石对顶砧的金刚石压砧周围布置测量线圈,对样品的交流磁化率进行测量[32—41]。
互感法进行交流磁化率测量的原理基于法拉第电磁感应定律
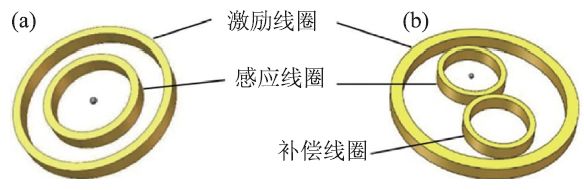
其中φ为回路磁通量,B为回路磁感应强度,S 为回路面积,法拉第电磁感应定律变化的磁通量会产生感应电动势。如图16(a)所示,当为激励线圈提供一个交变电流时,在激励线圈内部会产生一个交变的磁场Hac,处在Hac 中的样品被磁化后在感应线圈两端产生一个感应电动势E。通常如图16(b)所示,在激励线圈内放置一个补偿线圈,该线圈两端会因为交变磁场产生感应电动势E"。将感应线圈和补偿线圈串联反接,E'和E"相互抵消。线圈绕制参数的一致性以及感应线圈和补偿线圈在激励线圈中的对称性都会对抵消效果造成影响,因此总会有无法抵消掉的残余噪声存在。一般还在回路中加入一个微调线圈,进一步抵消噪声。此时整个回路输出电动势ε是非常微弱的,一般在nV 量级,使用锁相放大器对ε的幅值进行测量。
图16 (a)互感法单线圈结构;(b)互感法典型双线圈结构
对于体积为v,磁化率为χ的样品,通过锁相放大器测量到的信号幅值为
其中,f、i 分别是交变激励电流的频率和幅值,n、k 分别是激励线圈的匝密度和层数,N是感应线圈的匝数,D是激励线圈的内径。由此方法测量得到的磁化率χ是交流磁化率。在测量中,f、k、n、i、N、v、D都是常数,即χ与V 是成正比的,可以通过测量V 的变化趋势得到χ的变化趋势。但是通过V 对χ进行绝对测量是无法实现的,此方法仅能进行相对测量。
Viktor 等人提出了一种使用低频调制磁场降低测量时背景噪声的方法[35—37],使用这种方法对高压下样品的交流磁化率进行测量可以消除温度变化时的背景噪声,提高整个测量系统的分辨率。其基本原理是:当外加磁场大于临界磁场时,样品超导态会被破坏,转变为正常态,即交流磁化率由-1 变为0。临界磁场和温度存在以下关系:
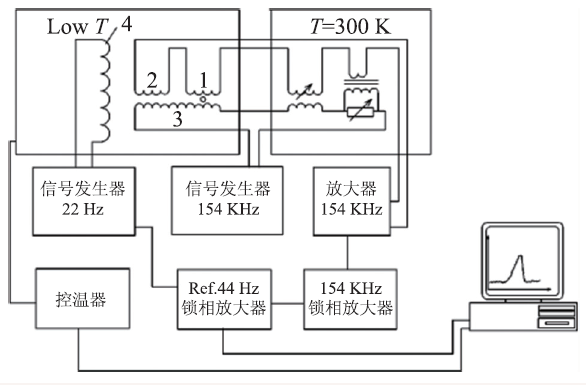
其中Hc为温度T 时的临界磁场,H0为温度0 K时的临界磁场。如图17 所示,在激励线圈3、感应线圈1、补偿线圈2 外部加入一个调制线圈4,调制线圈由22 Hz 的低频正弦波信号进行驱动。样品处于超导态时,当调制线圈产生的磁场小于临界磁场,样品仍然处于超导态,但是当磁场大于临界磁场,样品超导态被破坏,变为正常态。这种转变仅与磁场的大小有关而与磁场的方向无关,因此反向磁场同样会发生以上转变。在调制线圈产生的一个磁场周期中,被测样品发生了两次交流磁化率由0 到-1 的周期性转变。然后可以通过一个额外的锁相放大器锁定驱动线圈磁场频率的二倍频,在临界温度附近会产生一个突变的信号。低频磁场仅对处于超导态的样品有调制作用,周围环境并不会对低频磁场做出响应,从而可减小背景噪声。
图17 低频磁场调制法互感测量法测量超导材料的超导转变温度原理图[42]
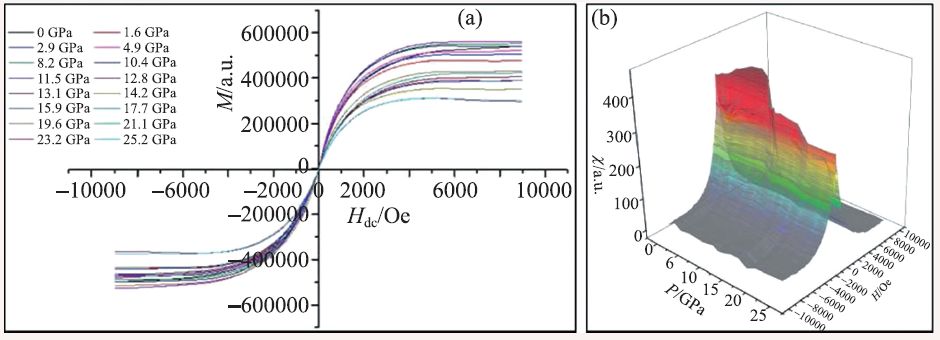
我们课题组通过分析现有高压下磁性测量技术,设计并搭建了高灵敏度、高稳定性的原位高压磁性测量系统,该系统基于金刚石对顶砧,能够给样品提供高压、低温、强磁场等极端条件,可以对极端条件下样品的交流磁化率、磁化曲线、超导转变温度等参数进行测量,系统提供了互感测量法和低频磁场调制法两种测量超导转变温度的方法。利用这一系统,我们对高压下铁的磁性转变进行了研究[41],如图18 所示,Fe 的结构相变α→ε伴随着磁性的转变,而相变之后的ε相铁的磁化曲线形状未发生改变,说明相变后的铁并非是顺磁性的,但是初始磁化率和饱和磁化强度都降低了,铁磁性被削弱。最近,我们利用该系统已经完成了H3S 超导Meissner 效应的实验验证,发现在压力149 GPa 时,超导转变温度为183 K[43]。
图18 (a)在不同压力下,铁的增量交流磁化率随外部直流磁场的变化;(b)各个压力下的磁化率曲线积分得到的不同压力下铁的磁化曲线[41]
本文主要介绍了拉曼光谱、红外光谱、布里渊散射、同步辐射X射线、原位电学、原位磁学等几种常见的基于金刚石对顶砧的高压下测量方法的原理和应用。随着实验技术的发展,已经有更多的测量方法和手段可以应用到高压研究中,提供了大量有价值的实验数据。自人们开始进行高压实验起,追求更高实验压力的脚步就一直未停歇过。特别是在近几十年,高压实验技术迅速发展,实验能够获得的极限压力值快速提高。面对随之而来的实验样品的尺寸变小以及金刚石的特殊结构等一系列问题,现有的很多与高压实验相集成的测量方法和手段有些力不从心。因此,在未来的高压实验研究中,使原位测量技术跟上高压产生技术脚步的道路依然漫长且富有挑战。
参考文献
[1] Mujica A,Rubio A,Muñoz A et al. Reviews of Modern Physics,2003,75:863
[2] Hemley R J,Ashcroft NW. Physics Today,1998,51:26
[3] Jayaraman A. Review of Scientific Instruments,1986,57:1013
[4] Parise J B. Reviews in Mineralogy and Geochemistry,2006,63:205
[5] Stoffler D. Science,1997,278:1576
[6] Williams Q,Hemley R J. Annual Review of Earth and Planetary Sciences,2001,29:365
[7] Housley R M,Dash J G,Nussbaum R H. Physical Review,1964,136:A464
[8] Clendenen G L,Drickamer H G. Physics Review,1964,135:A1643
[9] Moyzis J A,DePasquali Jr G,Drickamer H G. Physica Review,1968,172:665
[10] Debrunner P,Vaughan R W,Champion A R et al. Review of Scientific Instrument,1966,37:1310
[11] Duan D,Liu Y,Tian F et al. Sci. Rep.,2014,4:6968
[12] Drozdov A P,Eremets M I,Troyan I A et al. Nature,2015,525:73
[13] Brash JW,Melveger A J,Lippincott E R. Chemical Physics Letters,1968,2 (2):99
[14] Adams D M,Payne S J,Martin K. Applied Spectroscopy,1973,27 (5):377
[15] Huang Y P,Huang X L,Li W B et al. The Journal of Chemical Physics,2015,143:064505
[16] Huang X,Li F,Huang Y et al. Chinese Physics B,2016,25 (3):037401
[17] 张光寅,蓝国祥. 晶格振动光谱学,北京:高等教育出版社,2001
[18] 钟海庆. 红外光谱法入门. 北京:化学工业出版社,1984
[19]Wu X X,Ma F X,Ma C L et al. J. Chem. Phys.,2014,141:024703
[20] Whitfield C H,Brody E M,Bassett WA. Review of Scientific Instruments,1976,47(8):942
[21] Shimizu H,Sasaki S. Science,1992,257(5069):514
[22] Murakami M,Ohishi Y,Hirao N et al. Earth and Planetary Science Letters,2009,277(1):123
[23] Li F et al. Journal of Raman Spectroscopy,2012,43(4):526
[24] 杜建国,贺端威,高春晓. 矿物岩石高温高压实验与理论研究. 北京:地震出版社,2011
[25] Mao Z,Lin J F,Jacobsen S D et al. Earth and Planetary Science Letters,2012,331:112
[26] Li F et al. Applied Physics Letters,2006,88(20):203507
[27] Sinogeikin S V,Lakshtanov D L,Nicholas J D et al. Journal of the European Ceramic Society,2005,25(8):1313
[28] Hanfland M,Loa I,Syassen K et al. Solid State Communications,1999,112:123
[29] Birch F. Journal of Applied Physics,1938,9:279
[30] VAN DER PAUW L. Philips Technical Review,1958,20(8):220
[31] Chi Z H,Yen F S,Peng F et al. arXiv:1503.05331
[32] Alireza P L,Julian S R. Review of Scientific Instruments,2003,74:4728
[33] Jackson D D,Aracne-Ruddle C,Malba V et al. Review of Scientific Instruments,2003,74:2467
[34] Kim C C,Skelton E F,Osofsky M S. Physical Review B,1993,48:6431
[35] Kim C C,Reeves M E,Osofsky M S et al. Review of Scientific Instruments,1994,65:992
[36] Struzhkin V V,Timofeev Y A,Hemley R J et al. Physical Review Letters,1997,79:4262
[37] Timofeev Y A,Mao H K,Struzhkin V V et al. Review of Scientific Instruments,1999,70:4059
[38] Timofeev Y A,Struzhkin V V,Hemley R J et al. Review of Scientific Instruments,2002,73:371
[39] Yong Y,Zhai G J,Jin C Q. Chinese Physics Letters,2009,26:026201
[40] Gilder S A,Legoff M,Peyronneau J et al. Geophysical Research Letters,2002,29(10):30-1
[41]Wang X,Hu T L,Han B et al. Chinese Physics B,2014,23:070701
[42] Taylor R D,Pasternak M P,Jeanloz R. Journal of Applied Physics,1991,69(8):6126
[43] Huang X,Wang X,Duan D et al. arXiv:1610.02630
本文选自《物理》2019年第9期
2.漫画 | 2019诺贝尔物理学奖:流浪地球的无限种可能,及宇宙的昨天、今天和明天!
6.2018—2019 年度中国物理学会各项物理奖获奖名单及介绍