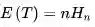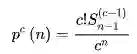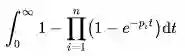如何用数学方法估算一个女生前男友的数量？

来自：知乎，作者：酱紫君

https://www.zhihu.com/question/38331955/answer/125686675

如果一个女生说，她集齐了十二个星座的前男友，我们应该如何估计她前男友的数量？

• 小学生：这个问题相当简单

公式：

数据：

{白羊座, 金牛座, 双子座, 巨蟹座, 狮子座, 处女座, 天秤座, 天蝎座, 射手座, 摩羯座, 水瓶座, 双鱼座}

实现：

N@# HarmonicNumber@# &@12

答案：

37.2385

-----------------------------------------

• 初中生：不知道要考虑分布吗？

公式：    

数据：

n=12

实现：

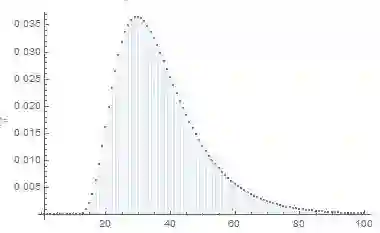
DiscretePlot[c!StirlingS2[n-1,c-1]/c^n/.c->12,{n,1,100}]

答案：

有10%的把握少于17个，有50%的把握少于35个。

有90%的把握少于55个，有99%的把握少于82个。

------------------------------------

• 高中生：知不知道人群中星座分布比例不均？

公式：

数据：

额外假设1：题主是中国人，所以使用中国的星座分布数据

额外假设2：题主是适龄青年，所以使用年龄18-36的星座分布数据

第一个是白羊座，然后是金牛，以此类推…

p={0.1028,0.0911,0.0843,0.0822,0.0848,0.085,0.0857,0.0795,0.0753,0.0761,0.0808,0.073}

注1：不要吐槽总和不是1，因为有舍入误差……

实现：

NIntegrate[1-Fold[Times,1,1-E^(-#t)&/@p],{t,0,9527}]

答案：

37.7424，就比均匀分布多了0.5个…

可以类比均值不等式理解为何分布默认均匀的时候最小

--------------------------------------

• 大学生：难道不知道上一任男友对下一次决策有影响吗？

比如……哦不……显然

上任是处女座，估摸着下任怎么着也不会是处女座了…

上任是天蝎座，那么我打包票，你不会也不敢有下任了…

然后顺便把上面的星座分布不均也考虑进去…

所以我们可以用一个转移矩阵来刻画这个情况。

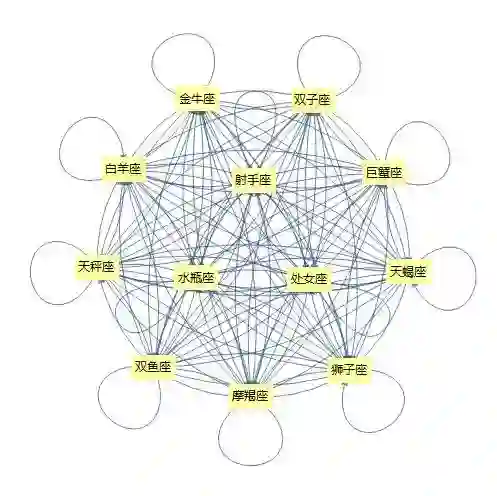
或者画成12个节点的加权有向图…

然后求这个加权图G的随机游走覆盖时间(Cover Time)

考虑到严谨性我应该证明一下上面的一堆公式，不过上面三个公式每个都能写篇大论文，短短篇幅说不清，所以解释就化归到这个问题一并解决…

随机游走

• 把12星座画成12个节点，然后可以作为下任的话就画个箭头
  

• 箭头有个粗细程度，这个叫加权，加权决定了选这个下任的概率有多大，实际概率波动不大所以不明显
  

• 分析这144个关系全都画出来就是上面这张图
  

• 选男友的过程数学上被称为图G上的随机游走

Cover Time

• 这些节点全部经过至少一遍所需要的时间叫做Cover Time

• 子问题包括各种著名概率问题，生日问题啊，赠券收集啊等等…
  

• 衍生问题还有复遍历，多重遍历什么的，可以有效用于氪金估计…
  

• 退化问题，退化为Tree的话可以相当有效的进行爬虫策略优化…

显然上面三个公式都是这个问题的特例

1、小学生：12阶非加权完全图的Cover Time

2、初中生：12阶非加权完全图指定Cover程度后的Time分布

3、高中生：12阶加权完全图的Cover Time

这个问题数学上来说的话不难，穷举所有路径首次通过时间的分布的平均值的交错和就行了...写成公式就是这样：

记A为G的所有可能通过的路径

虽然能写出公式然而并没有什么用，求解精确值还是个世界难题…

写成代码是这个样子的，复杂度足够让算法学家爆气…

幸好星座只有12个我的小CPU还能踉跄跑完...56个民族的话到宇宙灭亡也跑不完

而且蒙特卡洛效果也不太好，小规模精度不够，大规模基本跑不完…

一般可以用Matthews逼近来稍稍有效的求一下上下界…

见Markov Chains and Mixing Times一书

哦，忘记说计算结果了，初始节点对最后的结果影响不小，所以第一个男友很重要啊

第一任是处女座的话最小，只要31.64个，其他都在在35-38之间…
-----------------------------------------

• 社会青年：这种女孩子我见得多了

某些数理邪 教组织啊，宣传什么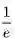法则，就那个传说中能找到最理想男友的法则...

无责任超链接：关于配偶选择理论的详细解释以及推广
http://www.kylen314.com/archives/5234

人一生中会遇到大约40有可能进行交往的对象，然后可以取前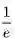也就是13个人为实验组，考察下质量然后放弃掉，然后后面27个只要有超过前13个中最强的就嫁了吧……

Well.....So,Reasons to believe that you are the 13th rebound guy...

简单地说就是找12个星座的男生采样比较均匀……

----------------------------------
唔，如果你相信真爱的话，说不定是这种情况：

-END-

---

●编号631，输入编号直达本文

●输入m获取文章目录

推荐↓↓↓

大数据与人工智能

更多推荐《18个技术类公众微信》

涵盖：程序人生、算法与数据结构、黑客技术与网络安全、大数据技术、前端开发、Java、Python、Web开发、安卓开发、iOS开发、C/C++、.NET、Linux、数据库、运维等。