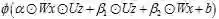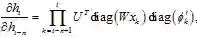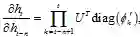Multiplicative Integration RNN-NIPS16 (1)
On Multiplicative Integration with Recurrent Neural Networks
Authors: Y. Wu, S.Zhang, Y. Zhang, Y. Bengio and R. Salakhutdinov
前言 :趁着远在西班牙的余温,在ICML的阅读周期内插入这篇被推荐阅读的文章,之所以想谈谈这篇文章的原因有3:1)文章的思路简洁明了,具有比较强的启发性;2)文章工作的完成度并不高,可以估计还会有后续工作进行探讨;3)这是一篇反常规的NIPS论文。接下来,带着这三个我的个人观点来看看这篇文章到底说了什么。
1 主要贡献和动机
文章的主要贡献可以用一句话概括:将RNN中的加性结构改为乘性结构。在加性结构中,RNN激活函数的形式为: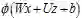
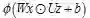
改为乘积形式的主要好处是什么?在加性结构中,Wx和Uz相互独立,这会使得优化过程可能被其中的某一项(数值较大的)所主导。而在乘性模型中,Wx和Uz能够起到相互调节(rescale)的作用。尤其是在进行梯度优化时,在适当的条件下乘性模型还可以起到避免梯度消失或者爆炸的作用。另外,泛化的乘性模型可以看做是早原加性模型中引入二阶项的形式,在不增加参数的情况下提高了模型的复杂程度。
2 乘性结构的泛化及其梯度
将乘性结构进行泛化,其形式为:
这个形式可以看作是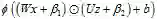
考虑乘性模型的隐层输出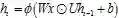
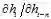
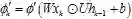 。对比加性模型的隐层输出
。对比加性模型的隐层输出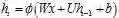 ,其偏导
,其偏导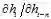 ,
,
其中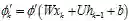
3 实验
作者用了大量篇幅的实验工作来验证MI-RNN的性能。我节选一些重要的实验结果加以说明:
a 梯度性质
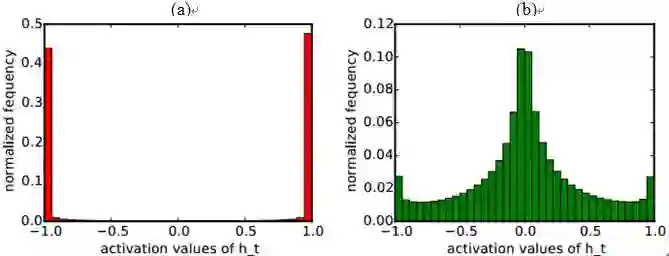
作者选用tanh作为隐层的激活函数,在Penn-Treebank数据集上进行验证,并将收敛后各隐层的激活函数的数值分布展示于图 1中。可以看到在实际运行中,乘性模型相比加性模型更不容易使激活函数达到饱和状态(tanh=±1)。当激活函数达到饱和状态时,梯度值趋近于0(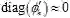
图1(a)加性结构RNN隐层输出的值分布;(b)乘性结构RNN隐层输出的值分布
b 参数W的初始化范围
加性模型的另一个问题是当Wxk和Uhk-1的数值大小不均衡时,容易导致优化会向数值较大的方向偏移。这个问题当输入xk为one hot表达时有更大几率发生,此时Wxk会明显小于Uhk-1,从而导致输入项很难起到作用。针对这一问题作者在实验部分,固定了参数矩阵U的初始化范围为[-0.02,0.02],调整参数矩阵W(输入相关)的初始化范围[-rw, rw],rw的数值从集合{0.02,0.1,0.3,0.6}中挑选,从表1可以看到相对于RNN,MI-RNN的性能受W初始化范围的影响很小。
表1 参数W的初始化范围对模型perplexity结果的影响
rw= |
|
|
|
|
Std |
RNN |
|
|
|
|
|
MI-RNN |
|
|
|
|
|
c 收敛速度及效果
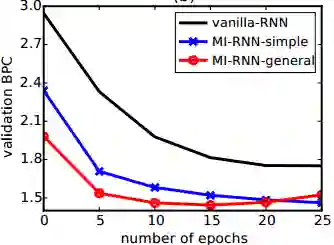
在收敛速度上,作者比较了vanilla-RNN(常规的RNN),MI-RNN-simple,MI-RNN-general(泛化的乘性模型)三者在训练过程中在validation set上的表现情况。从图 2可以看到,MI-RNN-general的收敛速度最快,并且MI-RNN-simple和MI-RNN-general的收敛速度明显优于vanilla-RNN。从所选用Penn-Treebank,text8以及HutterWikipedia的数据集上的表现结果来看,MI-RNN也有较为明显的提升。
图2模型的收敛速度比较
d 其他应用
在其他的应用领域,文中选用了语音识别,短语的表达学习以及语义理解三个应用场景。在这三个应用场景中,作者说明了MI-RNN同样适用于模型融合,结合其他RNN结构(例如,Skip-Thought model),甚至可以结合目前已有的RNN训练方法(例如,Reccurent Batch-Normalization),并且能够得到效果的提升。
总结 :文章的最后引述了Hidden Markov Model的例子用来认识乘性模型。令Uij=Pr[ht+1=i | ht=j], Wij=Pr[xt=i | ht=j], xt为one hot向量,ht=Pr[ht],则Wxt=Pr[xt | ht=j], Uht=Pr[x1, …, xt, ht+1]。因此ht+1=Wxt+1⊙Uht= Pr[xt | ht=j] Pr[x1, …, xt, ht+1]=Pr[x1, …, xt+1, ht+1]。当激活函数为Φ为线性时,MI-RNN可以被视为HMM在非线性情况下的扩展。另外,泛化的乘性模型可以看做是增加了二阶特征组合的加性模型的扩展。因此可以预见乘性模型对于加性模型的效果提升。
可以看到整篇文章在模型和理论部分论述的篇幅非常简单,取而代之的是大量篇幅的实验描述,这就是我所说的反NIPS论文常规现象之一。文章最大的疑问之处在于个人觉得乘性模型在理论上存在一定的适用范围,不恰当的参数初始化可能会使得乘性模型对比加性模型更不稳定,关于这一点很有可能会在不久的将来得到解答。