RNN | RNN实践指南（2）

 目录 

• RNN的基本结构

• RNN的实现

• RNN的调参

• RNN问题汇总

• RNN的相关应用

---

（接前文）

 2   RNN的实现

---

在目前这个阶段，要实现RNN已不再是什么难事，例如，tensorflow就集成了LSTM的实现，包括双向LSTM，都只需要通过一个简单的调用即可完成。但黑盒化实现的背后，会给我们在实际运用中带来理解上的额外开销，这也是为什么我会在讲解完RNN的基础理论模型后，仍然想要从实现的角度出发解释RNN实现的初衷：通过对RNN实现细节的理解，更加清晰地知晓RNN的相关优缺点。

为了方便解释，我用我所熟悉的Java语言写了一个有关LSTM和GRU的具体实现，具体的代码详见我的github项目：https://github.com/Allen517/rnn_demo。接下来，就RNN的源码来具体讨论RNN的重要细节。

 

 a   实践说明 

从实现的角度来看，我们可以将RNN分为三个部分：输入、神经元实现（对应理论部分的解码）以及输出。这三个部分的具体作用如下：

1） 输入。RNN的输入部分的实现主要负责对原始输入进行向量化。在实际的应用中，常用的向量化方式有：特征抽取和特征学习两类。其中特征抽取比较基础，由各领域具体的应用问题按要求抽取即可。输入端的特征学习则是RNN的学习机制的一部分，本质上是将原始表达做一次线性/非线性变换作为输入，而变换的方式（参数矩阵）在学习过程中通过优化得到；

2） 神经元实现。神经元实现对应具体的RNN核心架构，例如，选用LSTM作为神经元实现，则需在实现部分计算LSTM中的输入门、遗忘门、输出门、状态和隐层输出具体这五个量；

3） 输出。输出部分对应具体的应用。可以将神经元输出的隐层表达h看作是输入由RNN作用变换得到的特征向量。利用所得的特征向量，解决具体的应用问题，是输出部分的实现目标。例如，回归、分类、排序等等，都可以作为输出部分的模型实现。

 

补充知识： 在输入部分，我们将用表示学习方法得到特征抽取结果的也作为特征抽取的方法之一，虽然这部分的特征也是学习获得，但没有特征学习额外增加的线性/非线性变换； 在神经元实现部分，主要涉及RNN的模型架构，现在主流对RNN的模型修改都集中在这一部分，这也是现在关于RNN的主流论文做文章最多的地方。例如，LSTM、GRU、双向RNN、多层RNN结构、attention-based RNN等，目标是通过更改RNN的神经元实现或者模型结构，以得到更好的隐层表达h，应用到具体的任务中去。在后文我们会具体就这一部分的常见优化进行探讨； 在理解输出部分之前，我们可以尝试遗忘之前所有对RNN的介绍，将输出部分的实现理解为，我们目前得到了一堆有序序列的特征表达，如何利用这些特征表达解决具体的应用任务。目前个人认为重点针对输出部分做文章，经典的应用工作有：KDD15-Recurrent  marked temporal point processes: embedding event history to vector,  CVPR16-Structural-RNN: Deep learning on spatio-temporal graphs。这两篇论文工作的具体介绍之前有过重点介绍，读者可以自行搜索查阅:-)

 

 对应代码 

    在项目代码的rnn/cell/impl中对应实现了输入、神经元实现和输出三个部分，分别是InputLayer.java, LSTM/GRU.java, OutputLayer.java。由于特征抽取具有领域特性，会随具体应用而发生变化，因此我们在InputLayer.java中只实现了特征学习的功能，而相关特征抽取的工作，我们在utils/InputEncoder.java中展示了一组简单的示例代码。读者可以根据自己需要具体实现。

 b   RNN神经元实现部分的优化

由于输入和输出部分对应具体的领域和任务，我们在此不做过多讨论。我们仅就RNN在神经元实现部分的具体优化细节进行讨论。在关于RNN神经元实现部分的优化中，我们主要讨论：激活函数调整、加正则化项、采用dropout策略、梯度优化策略以及正交初始化这几项我所了解的主要优化策略。

 

I. 对激活函数调整

首先从激活函数谈起，神经网络的激活函数目前有三种常用的形式：sigmoid，tanh，以及ReLU。其中sigmoid和tanh的性质相当，适用场景不同。sigmoid函数的输出范围为[0,1]，在RNN的神经元实现中，一般可以作为门信息的激活函数，对信息起到约束作用。而tanh函数的输出范围为[-1,1]，在RNN神经元实现中，一般可以作为输出信息的激活函数，例如，LSTM中的状态以及RNN的隐藏层计算都采用了tanh函数。对sigmoid稍作变化可变形至tanh函数形式

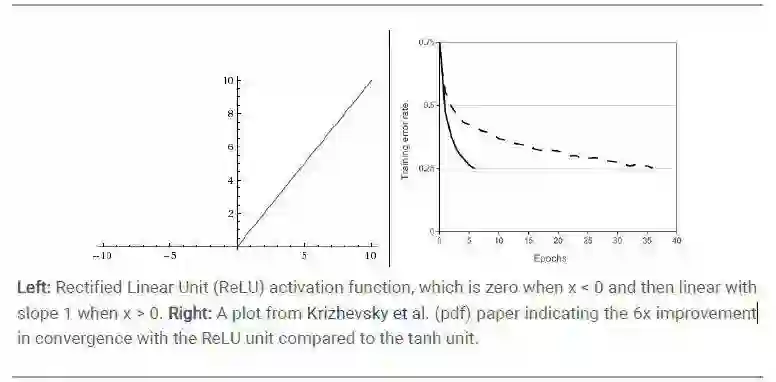
但tanh和sigmoid函数都在优化中存在一个比较严重的问题：函数值x对应的梯度在0附近较大。当x值较大或较小时，对应的梯度则会相对较小。当数值落在这些区域时模型会变得很难优化。一种解决方式是采用ReLU作为激活函数，ReLU函数的形式为max{0,x}，将输出强制为非负形式，并不对输出做smooth化。对比sigmoid、tanh和ReLU函数曲线的表现形式上来看，在ReLU函数上计算所得的梯度会较其他两种激活函数更大，不会因为陷入某些局部解而使得模型难以优化。Krizhevsky等人对比ReLU和tanh激活函数，展示了两者作为激活函数的收敛速度，可以看到两者收敛速度的差别（见图 7）[1]。但在RNN中选用ReLU替代tanh作为激活函数的问题是对模型的参数调整要更为小心，一旦学习率过大，则很有可能导致神经元中大量的连接不再起作用，从而导致模型的整体性能下降。

 

图 6 Sigmoid和Tanh函数的曲线形式

图7 ReLU函数的曲线形式以及与Tanh作激活函数时的收敛速度比较

 

II. 加正则化项

加正则化项可以保证模型参数的取值范围，防止模型参数优化到一个过大或过小的值上去。从贝叶斯的角度出发，也可以认为是给模型参数增加一个先验认识，防止模型出现过拟合问题。但加正则化项一般在RNN中不被经常使用。更多时候，正则项可以作为输入/输出的约束加入模型，我们曾在一个工作中，将一阶正则项加在了隐层输出上，目的是想让输出的隐层具有稀疏特点。

 

III. 采用dropout策略

dropout策略是在训练过程中随机去除RNN模型中的神经元节点（但仍保留去除神经元节点对应的连接权值）。这一方法起源于Hinton发表于2012年的文章[2]，对于那些采用小训练样本训练神经网络时，神经网络容易出现的过拟合问题，采用dropout方法可以解决一部分的过拟合问题。但dropout技术本身没有严格的数学证明和理论推导，在此也就不做过多的说明。具体对dropout实施也比较方便：在训练前对RNN隐藏层中的节点进行设置，保证它们在每一轮的训练迭代中以一定的概率不参与此次训练过程。采用dropout策略后，训练误差可能会变大，但测试误差可能减小，因此重点关注训练过程中模型在validation集上的表现情况，确定模型收敛与否。

 

IV. 梯度优化策略

关于梯度优化策略的具体选择可以参见我们之前所发布的公众号内容《梯度求解六式》。在模型调整初期，可以选用带动量（momentum）的梯度法优化求解，这是一种简单高效的实现，这样我们可以更多的关注在模型结构的调整，而不是优化方法上。在确定具体的模型结构后，要进一步地得到更好的优化结果，加速模型收敛速度时，可以选用Adagrad以及Adam算法。但我个人倾向于选择采用Adagrad作为调整初期的梯度求解实现，然后在具体的实施中采用Adam来进行梯度优化。

 

V. 采用正交初始化

一般对RNN参数矩阵的初始化有采用均匀分布、高斯分布的方法。但目前最好的初始化方法是选用正交初始化参数矩阵。关于正交初始化的细节我们在之前的公众号内容《为什么RNN需要做正交初始化？》中已有详细讨论。在具体的实施过程中，我们可以调用现成的SVD算法包，随机初始化一个与目标矩阵大小一致的矩阵K，利用SVD进行矩阵分解，然后取分解后与原矩阵大小一致的作为目标矩阵K的初值即可。

 

 对应代码 

在项目代码的rnn/utils/Activer.java中具体实现了激活函数sigmoid（对应logistic），tanh和ReLU；在项目代码的rnn/utils/MatIniter.java中具体实现了采用均匀分布、高斯分布以及正交方法的初始化方法；在项目代码rnn/cell/impl中包含的所有代码中，均实现了Adagrad以及Adam算法。

 

（未完待续）

参考文献

[1]Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deepconvolutional neural networks[C]//Advances in neural information processingsystems. 2012: 1097-1105.

[2] Hinton G E, Srivastava N, Krizhevsky A, et al. Improving neuralnetworks by preventing co-adaptation of feature detectors[J]. arXiv preprintarXiv:1207.0580, 2012..