R语言 | 构建信用评分卡模型

会员服务 ·

R语言 | 构建信用评分卡模型

2018 年 10 月 5 日 R语言中文社区

一 . 项目介绍

1.1 概述

如今在银行、消费金融公司等各种贷款业务机构，普遍使用信用评分，对客户实行打分制，以期对客户有一个优质与否的评判。其实信用评分卡还分A,B,C卡三类：

A卡（Application score card）申请评分卡

B卡（Behavior score card）行为评分卡

C卡（Collection score card）催收评分卡

信用评分是指根据银行客户的各种历史信用资料，利用一定的信用评分模型，得到不同等级的信用分数，根据客户的信用分数，授信者可以通过分析客户按时还款的可能性，据此决定是否给予授信以及授信的额度和利率。

1.2 数据来源

本项目数据来源于kaggle竞赛Give Me Some Credit，有15万条样本数据。

下载地址：

https://www.kaggle.com/c/GiveMeSomeCredit/data

1.3 目标

一般申请信用评分卡的构建

二 . 数据预处理

2.1 数据描述

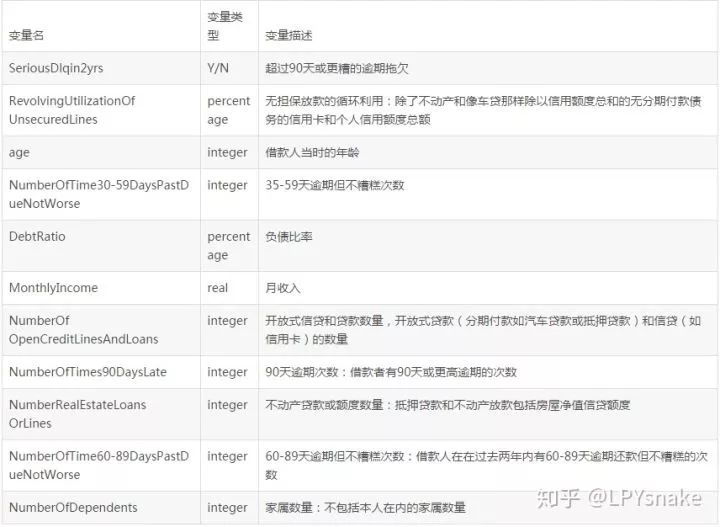
数据属于个人消费类贷款，只考虑评分卡最终实施时能够使用到的数据应从如下一些方面获取数据：

基本属性：包括了借款人当时的年龄。
偿债能力：包括了借款人的月收入、负债比率。
信用往来：两年内35-59天逾期次数、两年内60-89天逾期次数、两年内90天或高于90天逾期的次数。
财产状况：包括了开放式信贷和贷款数量、不动产贷款或额度数量。
贷款属性：暂无。
其他因素：包括了借款人的家属数量（不包括本人在内）。

2.2 数据处理

首先去掉原数据中的顺序变量，即第一列的id变量。由于要预测的是SeriousDlqin2yrs变量，因此将其设为响应变量y，其他分别设为x1~x10变量。

## 导入数据

rm(list = ls())

setwd('D:\\评分卡模型')

getwd()

a<-read.csv('cs_training.csv',header = T,stringsAsFactors = F)

str(a)

## 给列名重命名

colnames(a)

colnames(a)<-c("id","y","x1","x2","x3","x4","x5","x6","x7","x8","x9","x10")

summary(a)

2.3 缺失值分析及处理

在得到数据集后，我们需要观察数据的分布情况，因为很多的模型对缺失值敏感，因此观察是否有缺失值是其中很重要的一个步骤。在正式分析前，我们先通过图形进行对观测字段的缺失情况有一个直观的感受。

# 查看数据集缺失数据

md.pattern(a)

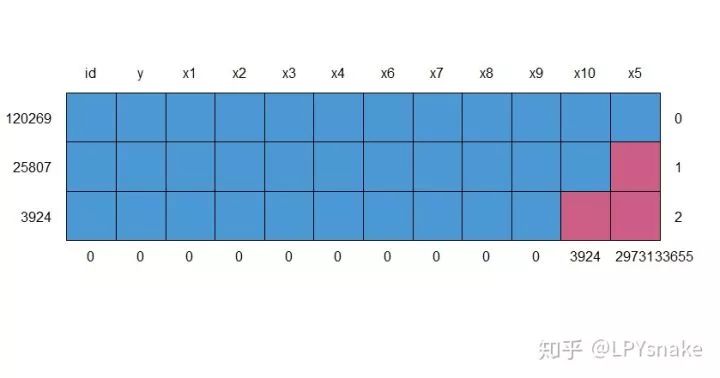
monthlyincome（X5）列共有缺失值29731个，numberofdependents(X10)有3924个。

# 对x5缺失处理

x5<-a$x5

x5_var<-c(

var="x5",

mean=mean(x5,na.rm=TRUE) , #na.rm=TRUE去除NA的影响

median=median(x5,na.rm=TRUE) ,

quantile(x5,c(0,0.01,0.1,0.25,0.5,0.75,0.9,0.99,1),na.rm=TRUE),

max=max(x5,na.rm=TRUE),

missing=sum(is.na(x5))

)

View(t(x5_var))

#用mean填补缺失值

a$x5<-ifelse(is.na(a$x5)==T,6670.2,a$x5)

# 对x10缺失处理

x10<-a$x10

x10_var<-c(

var="x10",

mean=mean(x10,na.rm=TRUE) , #na.rm=TRUE去除NA的影响

median=median(x10,na.rm=TRUE) ,

quantile(x10,c(0,0.01,0.1,0.25,0.5,0.75,0.9,0.99,1),na.rm=TRUE),

max=max(x10,na.rm=TRUE),

missing=sum(is.na(x10))

)

View(t(x10_var))

#用mean填补缺失值

a$x10<-ifelse(is.na(a$x10)==T,0.75,a$x10)

对于缺失值的处理方法非常多，例如基于聚类的方法，基于回归的方法，基于均值的方法，其中最简单的方法是直接移除，但是在本文中因为缺失值所占比例较高，直接移除会损失大量观测，因此并不是最合适的方法。在这里，我们使用mean方法对缺失值进行填补。

2.4 异常值处理

# 对x1处理

a$x1<-round(a$x1,2)

x1<-a$x1

x1_var<-c(

var="x1",

mean=mean(x1,na.rm=TRUE) , #na.rm=TRUE去除NA的影响

median=median(x1,na.rm=TRUE) ,

quantile(x1,c(0,0.01,0.1,0.25,0.5,0.75,0.9,0.91,0.99,1),na.rm=TRUE),

max=max(x1,na.rm=TRUE),

missing=sum(is.na(x1))

)

View(t(x1_var))

sum(a$x1 >1)#3057

boxplot(x1~y,data=a,horizontal=T, frame=F,

col="lightgray",main="Distribution")

#对x1进行盖帽法处理异常值

block<-function(x,lower=T,upper=T){

if(lower){

q1<-quantile(x,0.01)

x[x<=q1]<-q1

}

if(upper){

q90<-quantile(x,0.90)

x[x>q90]<-q90

}

return(x)

}

a$x1<-block(a$x1)

# 对x2处理

unique(a$x2)

sum(a$x2==0)

a<-a[-which(a$x2==0),]#删除年龄为0的异常记录

x2<-a$x2

x2_var<-c(

var="x2",

mean=mean(x2,na.rm=TRUE) , #na.rm=TRUE去除NA的影响

median=median(x2,na.rm=TRUE) ,

quantile(x2,c(0,0.01,0.1,0.25,0.5,0.75,0.9,0.99,1),na.rm=TRUE),

max=max(x2,na.rm=TRUE),

missing=sum(is.na(x2))

)

View(t(x2_var))

boxplot(x2~y,data=a,horizontal=T, frame=F,

col="lightgray",main="Distribution")

#对x2进行盖帽法处理异常值

a$x2<-block(a$x2)

# 对x3处理

unique(a$x3)

x3<-a$x3

x3_var<-c(

var="x3",

mean=mean(x3,na.rm=TRUE) , #na.rm=TRUE去除NA的影响

median=median(x3,na.rm=TRUE) ,

quantile(x3,c(0,0.01,0.1,0.25,0.5,0.75,0.9,0.99,1),na.rm=TRUE),

max=max(x3,na.rm=TRUE),

missing=sum(is.na(x3))

)

View(t(x3_var))

boxplot(x3~y,data=a,horizontal=T, frame=F,

col="lightgray",main="Distribution")

##盖帽法

block1<-function(x,lower=T,upper=T){

if(lower){

q1<-quantile(x,0.01)

x[x<=q1]<-q1

}

if(upper){

q99<-quantile(x,0.99)

x[x>q99]<-q99

}

return(x)

}

a$x3<-block1(a$x3)

……其他的变量都是用盖帽法处理的异常值，这里就不再一一列出。

把盖帽法的代码在下面列出来：

##异常值处理

#盖帽法

block<-function(x,lower=T,upper=T){

if(lower){

q1<-quantile(x,0.01)

x[x<=q1]<-q1

}

if(upper){

q99<-quantile(x,0.99)

x[x>q99]<-q99

}

return(x)

}

# 对y进行处理

a$y<-as.numeric(!as.logical(a$y))

2.5 变量分箱

证据权重（Weight of Evidence,WOE）转换可以将Logistic回归模型转变为标准评分卡格式。引入WOE转换的目的并不是为了提高模型质量，只是一些变量不应该被纳入模型，这或者是因为它们不能增加模型值，或者是因为与其模型相关系数有关的误差较大，其实建立标准信用评分卡也可以不采用WOE转换。这种情况下，Logistic回归模型需要处理更大数量的自变量。尽管这样会增加建模程序的复杂性，但最终得到的评分卡都是一样的。用WOE(x)替换变量x。WOE()=ln[(违约/总违约)/(正常/总正常)]。

library(smbinning)

library(prettyR)

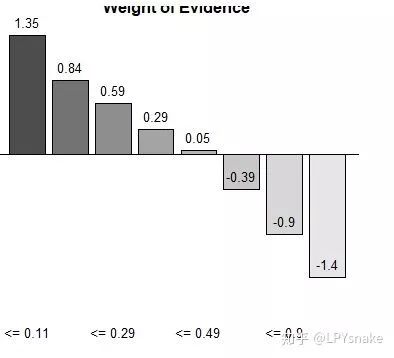
# 对X1分箱

x1<-smbinning(a,'y','x1')

x1$ivtable

par(mfrow=c(2,2))

smbinning.plot(x1,option = 'WoE',sub = "x1")

smbinning.plot(x1,option="dist",sub="x1")

smbinning.plot(x1,option="goodrate",sub="x1")

smbinning.plot(x1,option="badrate",sub="x1")

x1$iv

R_iv<-c(x1=x1$iv)

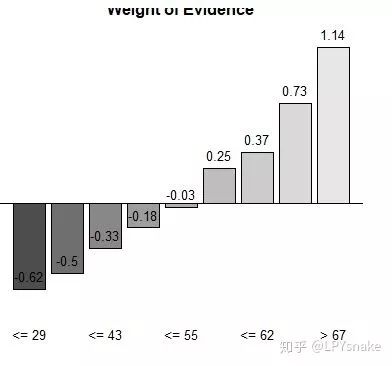
# 对X2分箱

x2<-smbinning(a,'y','x2')

x2$ivtable

smbinning.plot(x2,option = 'WoE',sub = "x2")

smbinning.plot(x2,option="dist",sub="x2")

smbinning.plot(x2,option="goodrate",sub="x2")

smbinning.plot(x2,option="badrate",sub="x2")

x2$iv

R_iv<-c(R_iv,x2=x2$iv)

# 对X3分箱

unique(a$x3)

x3<-smbinning(a,'y','x3')

x3$ivtable

par(mfrow=c(2,2))

smbinning.plot(x3,option="dist",sub="x3")

smbinning.plot(x3,option="WoE",sub="x3")

smbinning.plot(x3,option="goodrate",sub="x3")

smbinning.plot(x3,option="badrate",sub="x3")

x3$iv

R_iv<-c(R_iv,x3=x3$iv)

# 对X4分箱

x4<-smbinning(a,'y','x4')

x4$ivtable

par(mfrow=c(2,2))

smbinning.plot(x4,option="dist",sub="x4")

smbinning.plot(x4,option="WoE",sub="x4")

smbinning.plot(x4,option="goodrate",sub="x4")

smbinning.plot(x4,option="badrate",sub="x4")

x4$iv

R_iv<-c(R_iv,x4=x4$iv)

# 对X5分箱

x5<-smbinning(a,'y','x5')

x5$ivtable

smbinning.plot(x5,option = 'WoE',sub = "NumberRealEstateLoansOrLines")

x5$iv

R_iv<-c(R_iv,x5=x5$iv)

# 对X6分箱

x6<-smbinning(a,'y','x6')

x6$ivtable

par(mfrow=c(2,2))

smbinning.plot(x6,option="dist",sub="x6")

smbinning.plot(x6,option="WoE",sub="x6")

smbinning.plot(x6,option="goodrate",sub="x6")

smbinning.plot(x6,option="badrate",sub="x6")

x6$iv

R_iv<-c(R_iv,x6=x6$iv)

# 对X7分箱

x7<-smbinning(a,'y','x7')

x7$ivtable

par(mfrow=c(1,1))

smbinning.plot(x7,option="dist",sub="x7")

smbinning.plot(x7,option="WoE",sub="x7")

smbinning.plot(x7,option="goodrate",sub="x7")

smbinning.plot(x7,option="badrate",sub="x7")

x7$iv

R_iv<-c(R_iv,x7=x7$iv)

# 对X8分箱

x8<-smbinning(a,'y','x8')

x8$ivtable

par(mfrow=c(2,2))

smbinning.plot(x8,option="dist",sub="x8")

smbinning.plot(x8,option="WoE",sub="x8")

smbinning.plot(x8,option="goodrate",sub="x8")

smbinning.plot(x8,option="badrate",sub="x8")

par(mfrow=c(1,1))

x8$iv

R_iv<-c(R_iv,x8=x8$iv)

# 对X9分箱

x9<-smbinning(a,'y','x9')

x9$ivtable

par(mfrow=c(2,2))

smbinning.plot(x9,option="dist",sub="x9")

smbinning.plot(x9,option="WoE",sub="x9")

smbinning.plot(x9,option="goodrate",sub="x9")

smbinning.plot(x9,option="badrate",sub="x9")

par(mfrow=c(1,1))

x9$iv

R_iv<-c(R_iv,x9=x9$iv)

# 对X10分箱

x10<-smbinning(a,'y','x10')

x10$ivtable

par(mfrow=c(2,2))

smbinning.plot(x10,option="dist",sub="x10")

smbinning.plot(x10,option="WoE",sub="x10")

smbinning.plot(x10,option="goodrate",sub="x10")

smbinning.plot(x10,option="badrate",sub="x10")

par(mfrow=c(1,1))

x10$iv

R_iv<-c(R_iv,x10=x10$iv)

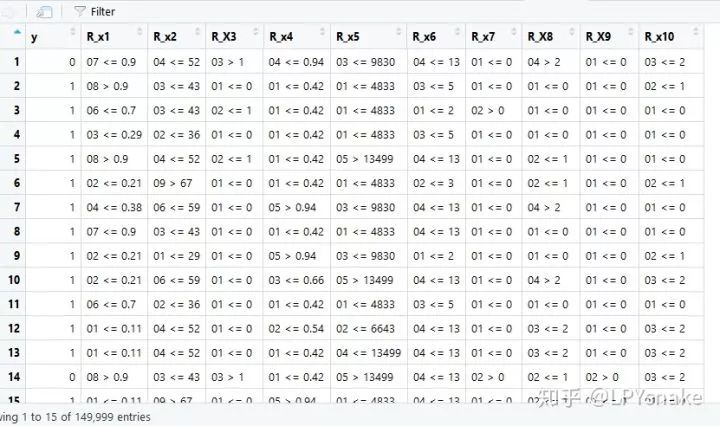
生成分箱后的新列

a2<-a

a2<-smbinning.gen(a2,x1,'R_x1')

a2<-smbinning.gen(a2,x2,'R_x2')

a2<-smbinning.gen(a2,x3,'R_X3')

a2<-smbinning.gen(a2,x4,'R_x4')

a2<-smbinning.gen(a2,x5,'R_x5')

a2<-smbinning.gen(a2,x6,'R_x6')

a2<-smbinning.gen(a2,x7,'R_x7')

a2<-smbinning.gen(a2,x8,'R_X8')

a2<-smbinning.gen(a2,x9,'R_X9')

a2<-smbinning.gen(a2,x10,'R_x10')

a3<-a2[,c(2,13:22)]

三. 构建建模

# 构建逻辑回归模型

cred_mod<-glm(y~.,data = a3,family = binomial())

summary(cred_mod)

四. 构建评分卡

4.1 对变量进行打分

# 对模型的变量进行打分

# score=A-B*log(odds)

cre_scal<-smbinning.scaling(cred_mod,pdo=45,score=800,odds=50)

cre_scal$minmaxscore

cre_scal$logitscaled

4.2 生成每行对应的分数

#生成每行对应的分数

a4<-smbinning.scoring.gen(smbscaled=cre_scal, dataset=a3)

boxplot(Score~y,data=a4,horizontal=T, frame=F, col="lightgray",main="Distribution")

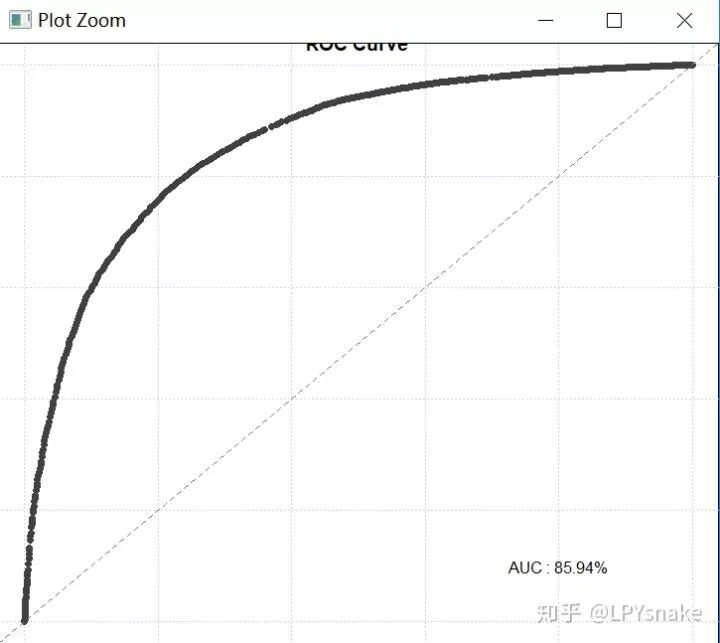
4.3 画ROC曲线

## 画ROC曲线

smbinning.metrics(a4,"Score","y",plot="auc")

模型评估

通常一个二值分类器可以通过ROC（Receiver Operating Characteristic）曲线和AUC值来评价优劣。

很多二元分类器会产生一个概率预测值，而非仅仅是0-1预测值。我们可以使用某个临界点（例如0.5），以划分哪些预测为1，哪些预测为0。得到二元预测值后，可以构建一个混淆矩阵来评价二元分类器的预测效果。所有的训练数据都会落入这个矩阵中，而对角线上的数字代表了预测正确的数目，即true positive + true nagetive。同时可以相应算出TPR（真正率或称为灵敏度）和TNR（真负率或称为特异度）。我们主观上希望这两个指标越大越好，但可惜二者是一个此消彼涨的关系。除了分类器的训练参数，临界点的选择，也会大大的影响TPR和TNR。有时可以根据具体问题和需要，来选择具体的临界点。

如果我们选择一系列的临界点，就会得到一系列的TPR和TNR，将这些值对应的点连接起来，就构成了ROC曲线。ROC曲线可以帮助我们清楚的了解到这个分类器的性能表现，还能方便比较不同分类器的性能。在绘制ROC曲线的时候，习惯上是使用1-TNR作为横坐标即FPR（false positive rate），TPR作为纵坐标。这是就形成了ROC曲线。

而AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

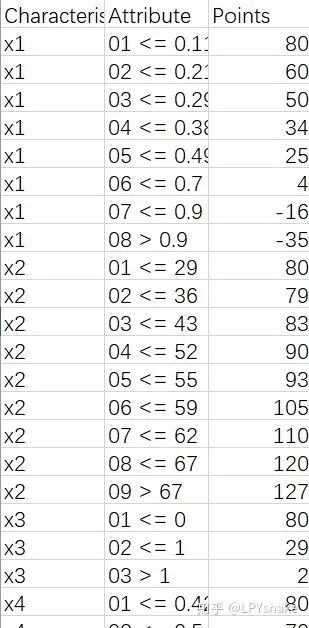
4.4 生成评分卡并导出

##生成评分卡并导出

scaledcard<-cre_scal$logitscaled[[1]][-1,c(1,2,6)]

scaledcard

scaledcard[,1]<-c(rep("x1",8),rep("x2",9),

rep("x3",3),rep("x4",5),rep("x5",5),

rep("x6",5),rep('x7',2),rep('x8',4),rep('x9',2),rep('x10',4))

write.csv(scaledcard,"card.csv",row.names = F)

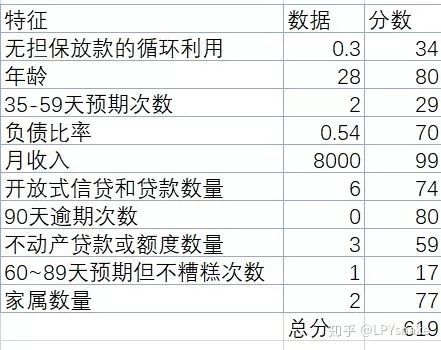
4.5 个人评分计算案例

公众号后台回复关键字即可学习

回复爬虫         爬虫三大案例实战
回复 Python 1小时破冰入门

回复数据挖掘   R语言入门及数据挖掘
回复人工智能   三个月入门人工智能
回复数据分析师  数据分析师成长之路
回复机器学习      机器学习的商业应用
回复数据科学      数据科学实战
回复常用算法      常用数据挖掘算法