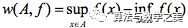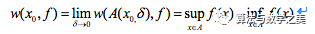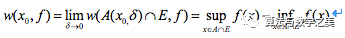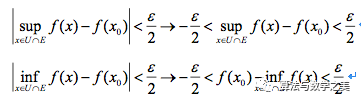关于黎曼积分的思考——谈黎曼积分的定义观念

2017 年 8 月 23 日 算法与数学之美 beerht

关于黎曼积分的思考——谈黎曼积分的定义观念

从点到无穷——从测度的基础谈起

重新审视可积条件本身“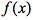在[a,b]上的一切不连续点成一零测度集”，这里的关键词是“测度”，因此首要的关键问题在于何为“测度”？传统意义上的测度有长度、面积、体积等，我们试图猜测一下，测度的抽象意义可以如何来描述？

前面已经提到过，传统测度计算中，点被认为是质点，这个思维最大的悖论在于在有穷物事中引入了“无穷”概念，任意的线段均含有无穷个点。这在根本上导致了对点区间本身描述的困难。反思初等数学中点概念的生成，从根本上讲，因为初等数学的描述中往往无需涉及“点”本身的特性，只需实现其对象化令其能够成为分析的基准和桥梁即可——这也就可以解释何以康托尔之前的科学家都尽力规避“无穷”这一概念。高斯等人采取了折中的理念，即承认无穷作为过程的存在而否定其作为对象的存在。事实上，回避“无穷”概念的本质还在于从根本上回避了“点”本质的明确。而“点”本身始终作为一个神秘的物理实体对象而被讨论所规避——这种观念实际上是一种视觉直观抽象的印象产物。而要完成“测度”的定义。首先必须要对“点”做出准确的定义——必要的是，这个定义必须充分兼容经典视角下的初等数学关于“点”的认知。

首先，我们观察传统的点认知，可以确定无疑地说，这个视觉心理的产生是以直观的视觉极限为形象基础的，其次，点概念的突破关键在于对“质点”本质的澄清，传统上认为质点有质量无大小，实际上只是一种分析效果等价思维导向下的一种模型产物——即以过程本身为线索，如若奉行这一思想，可以撇除物理过程分析中的次要因素。从此可以看出，工具本自概念思想，而概念本身往往也是工具之一。我们往往无以从根源上实证，由此可知数学是以认知本体为起源的相对实证形式系统，所谓的不完备定理，从最朴素的角度来理解，若逻辑体系中的数理关系的描述真的得以完整无误地归纳全部的过程属性信息，则本体无以证实其自身的完备性——因为完备性蕴含于本体之中，欲证实本体之完备，则必先于本体之逻辑衍生物中寻求论据，是以陷入循环论证之陷阱。

于是，欲弄清“点”的概念，则又不得不先诉诸“无穷”的概念认知。认知这就不得不引起我们对康托尔理论的反思与猜想——即朴素集合理论在康托尔的头脑里是如何被萌生出来的？

首先，“一一对应”这一思想是如何被琢磨出来的？从表面上看，即实变的“实”概念得以从此确立。康托尔所认为的“实”并非是高斯、柯西概念中的“实”（高斯、柯西概念中的“实”始终脱离不了“量值”的核心观念），康托尔所认为的“实”是以“逻辑实”为基础的，事实上，康托尔这种思想的背后蕴含了浓厚的莱布尼兹的形式主义符号逻辑思想——莱氏的重要思想在于他认为任意的逻辑对象都应该与其他逻辑对象在符号逻辑关系上具备明确的、无疑的结论，即认为以逻辑关系为核心，逻辑的关系可以归纳一切。这一点完全可以视为他关于数学自明性的认知的基础（牛顿等人的数学自明性则建立在认为存在绝对逻辑对象的基础上，例如绝对的时间、空间和质点），同时也是莱氏所谓“要想解决争议，动笔在纸上算一算就清楚了”的逻辑基础。由此，康托尔在传统的潜无穷理解的基础上衍生出了对“无穷”的集合化理解——即既然“潜无穷”是一种针对不断延展的过程的描述，那么这种描述本身就可以视为一个“元素”，存在多少种描述形式，就存在多少种“潜无穷”，而一般意义上所谓的“无穷”，则可以视为本质上是一个具备了共性的函数集合，当关系运算纯粹在数值关系上时，“无穷”则又完全可以压缩为一个“广义抽象值”来对待和理解——由此，“无穷”又获得了“广义数”的存在形式。由此，无穷的“实”得以确立。所谓“实”是源于对于广义逻辑对象及逻辑关系的承认，也就是说传统理解上的“证明”实际上是将数量关系的根源落实在量和值的认知之上，而数学的自明性依据自此从“直观的实在性”转入了“广义的相容性”。换言之，逻辑体系的构造旨在“调和”，不能调和则设定某一前提下力求能“凑合”，我们只能追求尽可能完美的逻辑系统。当逻辑系统出现悖论时，原则上应该诉诸于逻辑系统源头概念的本体的进一步抽象回归——这是保障既有逻辑理论体系成果安全无虞及其与未来新生逻辑系统无缝衔接的重中之重。

要回答点大小的问题，必须让点概念从物理实体的框架中解脱出来。由上述可知，“无穷”是为一个集合，则点实际上是无穷划分的产物，即一种划分。也就是说，从此不再以“点动成线”为思维起源，而是直接面向先在的、离散的、有限的实体进行划分。换言之，在“实体数”的基础上设立了“抽象数”的概念，“抽象数”是对区间边界的标定，我们可以想象是在原来被认为是“质点集合”的各个实体数区间之间设定了“隔板”，这些“隔板”就是抽象数。实体数的值越接近抽象数（实体数仍是被认为可运动的），则认为到达了抽象数。测度不再是由实体数的计算得到，而是以抽象数这些“标杆”之间直接计算的距离为准。

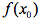
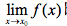
由此，函数在某点的值的准确描述应该是“函数在某抽象数上的值”，即获得了的存在形式（前提是该极限存在），而回归到定义域上则有，由此可知从区间极限的角度来看，抽象数位置处的振幅实际上是实体数收敛的结果。参照“无穷”的广义抽象数形式的定义，所谓收敛，实际上是一个实体数集合的运动能够映射到一个半径极限为0的邻域，所谓发散，即该集合的映射产物是一个半径极限非0的邻域。

为什么需要引入“振幅”的概念？

那么究竟为什么需要振幅这一概念呢？怎么想到把连续性的论证和振幅概念的引入挂上钩的？这还要先从连续性论证的困境重新说起。某个区间的函数振幅的定义为：

振幅=函数上限值-函数下限值

那么，当限定该区间时，

上述的这个描述形式我们不难理解，我们试图从这里摸索一下引入振幅的必要性。传统上认为，从“定义域点-值域点”的关系来看，函数是一一对应的静态关系，引入振幅的原因很有可能源于对函数本质属性认知的一种动态化的扩展理解。最令人疑惑的是，既然有振幅，为什么没看见振动？如果说振动是“潜在”的，那么应该如何理解这种振动？假设以不改变连续点位置为前提条件，令函数曲线（一维的姑且想象为弦）沿Y坐标轴做“面积守恒”的垂直振动，才符合R可积函数的要求。那么从振动的角度来描述面积守恒，究竟揭示了函数什么样的深刻内涵呢？

思想总是先从问题中来。问题总是对某种困境的表达。回顾牛顿的微积分理论，其最大的问题在于无穷小问题，这一问题直接扼住该理论的命脉。在微分过程中，从静态函数的角度上来看，极小的定义域微元划分反映到值域上，仍然存在值的差异。如果说这种值的差异确是不应回避的话，那么，究竟要如何建构积分的理论基础呢？

回顾书中的定义，实际上所谓点振动是以区间振动为依据推导得到的，而区间的振动则是以该值域区间内距离测度来衡量的。由此可知所谓振动，是指值域点位置的变化，即指“点的位置变化测度”，即承认微分中值的变化。试图猜测一下黎曼的初衷：要实现可积，那么从数值的角度上看，积分收敛是必然的；既然收敛是必然的，那么就有必要将收敛在分析意义上的概念在数理逻辑层面阐释清楚。基于规避无穷小量的基本原则，必须首先充分承认值的微小变化所造成的运算差异，从而间接地借助上下确界相等的夹逼原理可以确立积分的存在性（“存在即合理”，这里的“存在”指的是作为抽象数外在体验的数值的“存在”）。

可以看出，牛顿基于视觉直观引入纯粹的流数概念，其实是试图在无差量计算体系下直接纳入绝对的“无穷小值”思想（瞬的思想即无穷小量，牛顿未能调和而转向了本体不明的“无穷小值”）。而黎曼的定义则是必须建立在抽象数思想和测度论思想的基础上的。借由这些基础，黎曼将积分的存在性问题转化为了测度（抽象测量）结果的存在可能性问题。计算其实并非一种绝对，而其实质也只是和物理实验的测量一样，只是一种集合表征的逻辑体验（尽管这种体验已经是极限，但也与本体存在距离，这能够较好地协调和解释微积分计算的不完备性，即承认计算并非“绝对真”表达，而也只是“近似真”的表达。这其实也是最初引入“0”以及后来引入无穷作为广义数的思想基础）。上述称谓“夹逼原理”而非“夹逼准则”，是因为夹逼在值逻辑的层面始终成立，原因无他，依据排中律和同一律而已。换言之，夹逼原理成立的理由是“非如此则逻辑无以成立”。

由此可知，“振幅”似乎只是黎曼积分的一种自然而然的副产品。

从另一个角度对黎曼的初衷进行猜想：如果把函数的各段“起伏”乃至各点起伏认为是一种振动产物的话（无穷间断点可以视作持续地正向振动，有限间断点则可以视作振动的局部两侧振幅不等所导致的“断裂”效应），则在振动的宏观背景下来看，函数形态只是振动的某种产物，将视角切换到以振动为中心，则既然函数本身要求可积，那么由振动所覆盖的等价函数集中任意函数的可积似乎应该成为函数可积的数理渊源，同时也是研究振动的必要条件。

上述的猜测看似是对的，但有关键问题尚未明确：

（1）为什么就能把函数形态看作振动的产物呢？同时，振动本身的可积为什么也是函数R可积的必要条件？

（2）把视角转移到以振动为中心的好处是什么？或者说，这种思路是针对什么问题而来的？

这些问题首先应归结到“振动本身的原型是什么？”这一问题上来。那么首先要问：

（1）振动的独立对象是以点为单位还是以整体函数曲线为单位？还是别的？

前面已经说过，根据书中的分析，并没有定义一种振动，易知将点沿函数曲线运动的幅度视之为“振幅”。那么有没有另一种基于振动原型的解释呢？

假设以函数沿线各点为单位，则该点的振动与相邻点之间的运动完全独立，函数曲线可视作这些点随机运动（随机运动归纳了确定性运动，这里暂且借用该词的含义来进行笼统描述）的某一样值，如果是这样的原型，由于振动的随机性，很难让人联想到“振动可积”对“函数可积”的必要性意义。因为要约束这种随机，则必然存在规则（尽管这些规则尚不清楚），于是又要问这些规则何以应该如是被确立出来。因此，纯粹以点为单位的自由振动成为原型的可能性可以排除。

假设以函数曲线整体为单位，则振动本身的变化无疑会引起曲线的形变，而要求其保持“面积守恒”，那么这样的振动变化方案存在（即在曲线附近有若干种这样的方案）吗？但如果将这种振动的单位拆解为逐个微分段，则答案是一定的。将同一划分下的各段函数曲线打乱后任意排序，即可得到一个振动后的新函数，而面积尽皆相等。

也就是说，在曲线此起彼伏的各种方案里（假设这些曲线的面积均相等），这实际上构成对全体函数集合的一个等价划分。黎曼的视角并非沿袭“积分收敛——函数特性”这一基于数值特征关系双向对应的认知角度来看待积分，而是以面积为立足，通过确立面积的存在性，进而用夹逼原理得出函数曲线本身的普遍性，即建立了“面积-函数集”的映射思想，将全体的函数视作广义面积（包括无穷大以外）为划分的集合，也就是说，黎曼关于振动的设想其实可以理解为在集合等价划分思想指导下的函数各段（这个振动不是随机的，而是随面积要求为确定性的）的序列集合图景。进而引申到点振动原型。

这样认识积分带来的好处究竟是什么（以至于后世终以黎曼命名微积分）？一般而言，一种新的视角必须相对既有的认知体系更及于本质，才是一种有价值的新视角。那么这样设定的振动究竟对揭示函数内在性质增加了什么样的信息？以一个函数等价集合而论，在函数曲线各段“此起彼伏”的“振动”里，“可积”被放在了以各段振动为中心的视角里来看待。而各段振动构成了点振动的理论基础（这一点可以从书中点振幅由半径极限为0之区间振幅推导得出而获知），由此，面积等价关系完成了振动原型的搭建，振动原型又引申出点振幅的概念，由此点积分测度这一很“玄”的抽象表达即得以实现简约直观的数学表达。反过来，我们可以确立这样一个问题作为点振幅概念的引导问题：既然点集是疏朗的，要用点集重新解释积分，则积分运算就必须基于点集合测度，那么点积分测度如何定义呢？

从这一点来看，点振幅的意义不仅仅局限于积分运算范畴，更重要的是对广义数运算的归纳启示——示范了以点集合为基础来理解数的基础，则0和由此获得了其作为集合参与数值运算的合理性意义依据，即运算的上界、下界相等即作为其成为“独立数”的充分理由，从而可以在收敛运算情景上完全地获得“广义数”的存在方式；而在发散运算情景中，其计算结果实际上构成无穷集合与无穷集合之映射，不应被其“数的表达形式”所迷惑。

进展到“点”的振幅，这里所说的点是“抽象数”的指代点，那么

考虑到函数定义域的影响

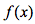
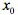
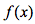
试证明“在点处连续等价于在该点振幅为0”来试验一下这种观点的优势

自证明思路：

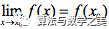
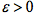
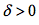
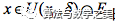
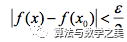
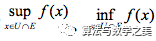
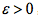
既然连续，则根据数学分析中的极限定义可知满足，则对任意，必然存在，满足时，均有，则易知也服从此规律，因此对任意有

上两式相加后可得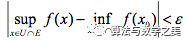，，由此可知连续是振幅为0的充分条件。

反过来如果振幅为0，则易知该点处于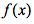定义域内。

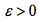
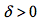
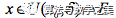
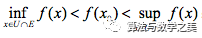
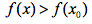
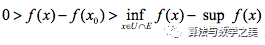
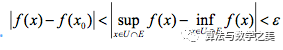
于是有任意，均存在，满足时，，由振幅定义可知，则对于，则有，而对于，则有，于是有因此连续

从证明的思路对比来看，引入振幅的最大好处就是函数在某抽象数点上的值的确定性问题被转化为“值的变动”问题，值差则被归结为其在实在值域上的极限值（这同样也就是魏氏极限定义何以超越前人的根本所在，关键在于颠覆了对前人关于数的本质认知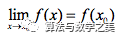，中等式左边的各个代数符号都指代“抽象数”，而等式右边的代数符号则指代“代数值”）。这样做之所以有好处，就是将“连续性”集中于一个“抽象数”点的论证拓展为对一个“实在值”区间内的论证。（这么做其实是很难的，作为质性定义，抽象数往往利于揭示概念本质而短于计算应用，之所以要建立抽象数和实在值的关系，本质上还是为了能够让计算尽量回归到实在值域中来），说白了，从开展分析的角度上讲，极限定义的最大好处是将极限的数值关系内涵说清楚了，而振幅定义的最大好处就是把在一个孤点的连续性问题用“幅度变化”的数值关系指代清楚了。

至此，点的概念算是说清楚了，测度究竟是什么还没说清楚，简而言之，点概念需基于集合理论，那么测度论则无疑是基于点集合概念理论的（实无穷概念需基于测度理论）。我们可以这样猜测：狭义的测度可以理解为点域的“无穷维尺度”，而广义的测度实际上是一种作用在点域上的逻辑关系运算（一切数值运算的核心是逻辑关系）。测度的核心问题是“可测”，即运算的收敛性问题。从上述关于振幅的演绎中可以看出，点测度被视为区间测度的极限，于是我们试图定义测度的概念：

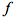
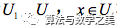
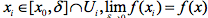
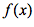
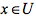
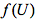
设点集合为U，作用于该集合之上的函数为，若存在任意划分，均有，则称在x上的测度。若上式对任意均成立，则称为f在U上的测度。

相关启示

启示一：数学符号形式的视觉心理是数学学习的重要基础。没有适当的符号视觉心理作为支撑，数学书籍的阅读和对形式演绎的开展是极其艰辛而困难的。反之，若是建立了良好的视觉心理，则阅读数学书籍实与文学、哲学、历史书籍之阅读并无二致。要建立良好的视觉心理，离不开对数学符号描述的理解，关于这一部分的内容，容另文阐析。

启示二：数学的证明本质上仍是以值逻辑为依据的。尽管数值获得了“测度”的存在形式，但从实际上来讲，数值仍是唯一可信任的依据，原因如下：其一、数值是抽象领域在可操作层面的度量极限；其二、无论对数值的认知为何，只要产生数值本身的逻辑情景一定，则数值必然具有绝对的唯一性和排他性，这本身就匹配逻辑基本原理中的同一律和排中律。从根本上说，数值的这些属性不是人为强行赋予的，而是可确逻辑的本征。即没有能够不存在于表达中的逻辑具体，也因此我们始终只能接触到具体的逻辑模式而无法接触到逻辑的真正本体。

启示三：实变函数实际上是建立在将数字意义绝对化、数值计算意义相对化的前提下的一门理论。类比数学分析的证明中频繁使用点邻域的情况（这么做是为将极限问题从极限符号中解放出来研究），实变函数涉及点集的大量运算也是为了把许多“点”的问题放到“集”里面来解决，同时，由于获得了测度的存在形式，数值的计算可以如同传统数学运算一般放心地进行。抽象化、数值化、关系化是分析逻辑常用的三步曲。

高质量延伸阅读

☞ 深度神经网络中的数学，对你来说会不会太难？

☞ 编程需要知道多少数学知识？

☞ 陈省身——什么是几何学

☞ 支付宝人脸识别的技术高大上，似乎是技术背后，的那个人做了场演讲

☞ 曲面论

☞ 曲面论（第二讲）