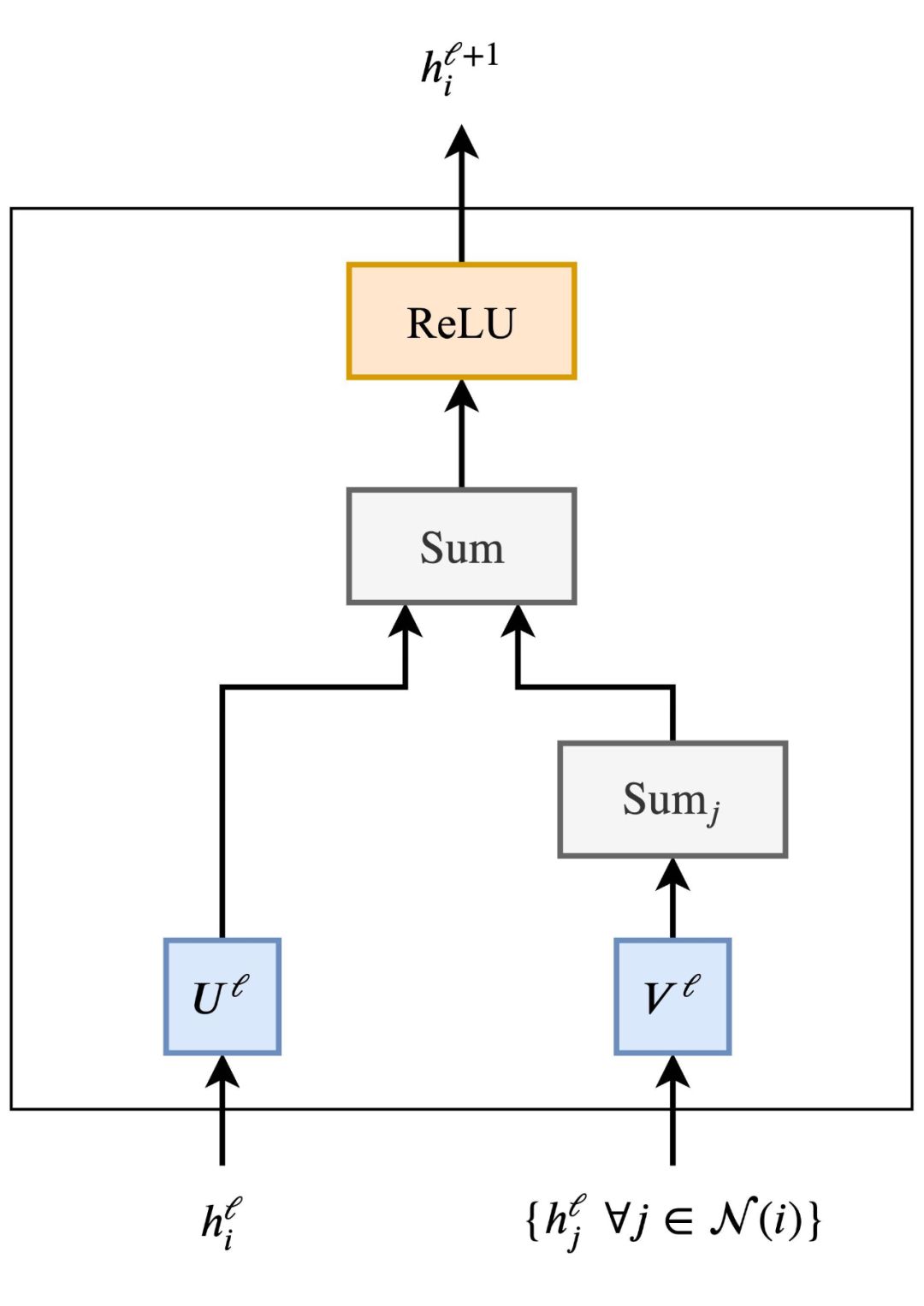
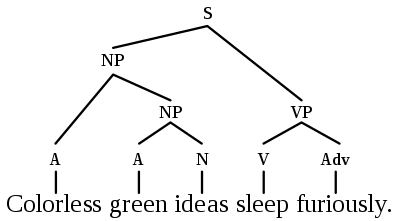
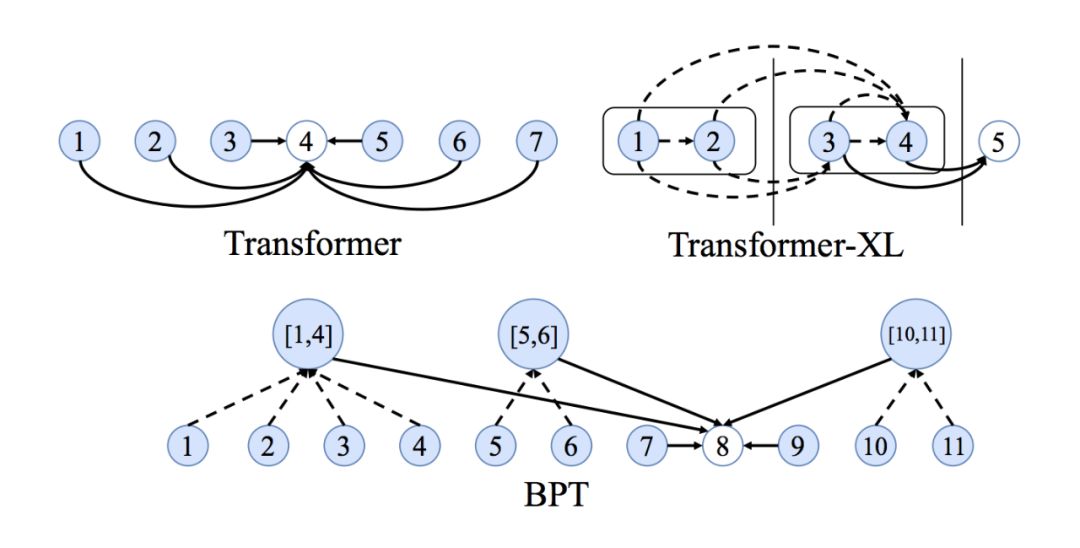
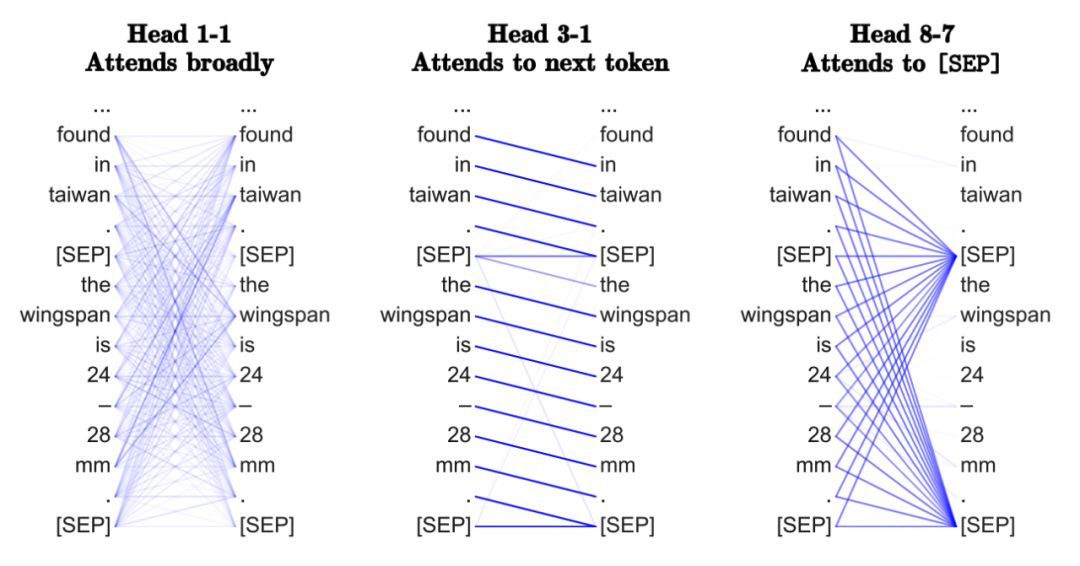
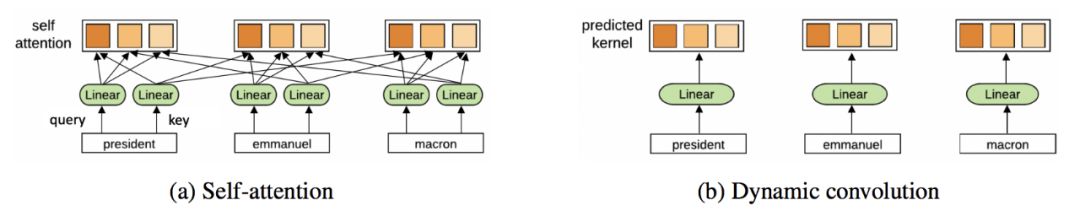
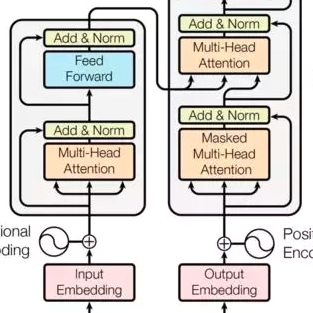
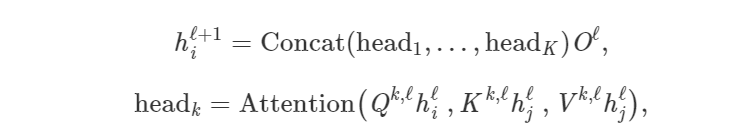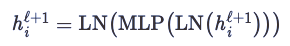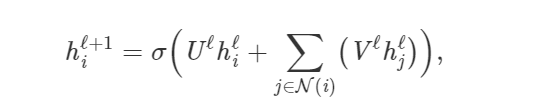原来Transformer就是一种图神经网络，这个概念你清楚吗？

会员服务 ·

原来Transformer就是一种图神经网络，这个概念你清楚吗？

2020 年 3 月 1 日 机器之心

选自NTU Graph Deep Learning Lab

作者：Chaitanya Joshi

机器之心编译

参与：一鸣、杜伟、Jamin

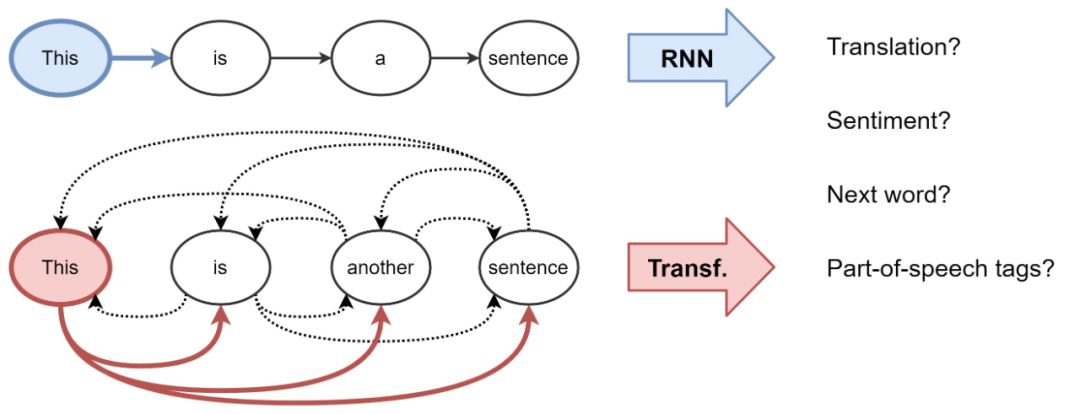
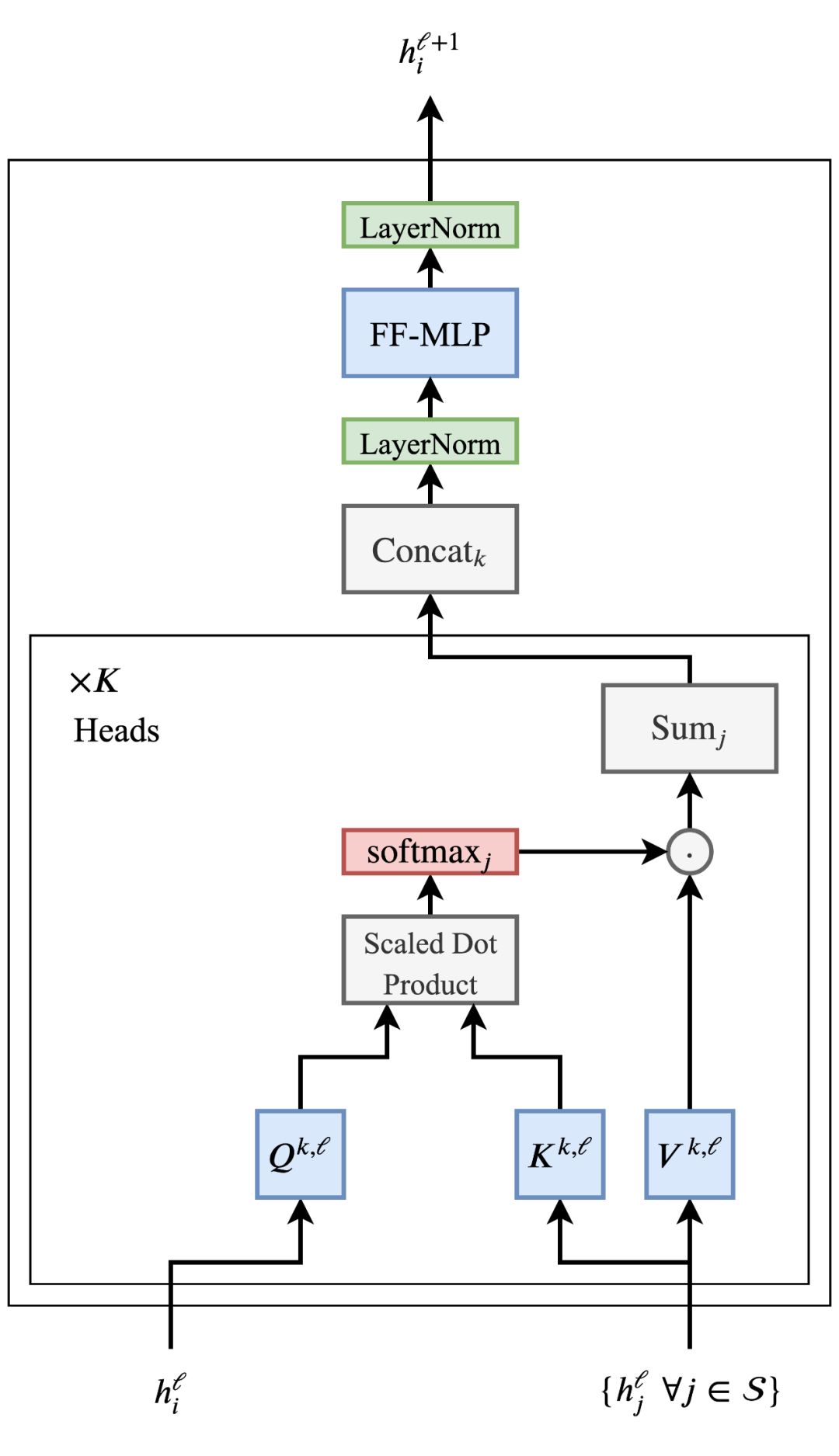
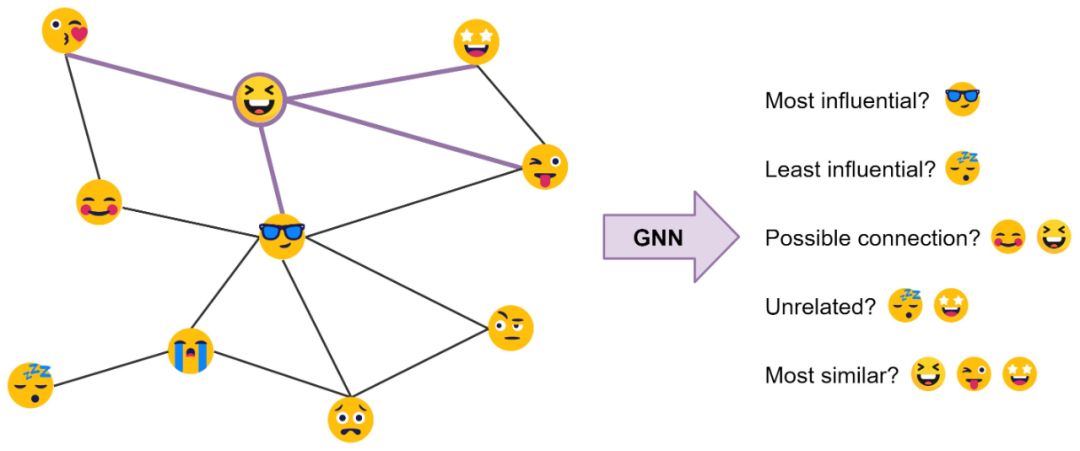
Transformer和GNN有什么关系？一开始可能并不明显。但是通过这篇文章，你会从GNN的角度看待Transformer的架构，对于原理有更清楚的认知。

有的工程师会问这个问题：图深度学习听起来不错，但是有没有商业上的成功案例？它是否已经在实际应用中使用过了？

除了一些以下企业中的推荐系统，如 Pinterest、阿里巴巴和推特，实际上在商业中已经取得成功的案例是 Transformer，它极大地改变了 NLP 业界。

通过这篇博文，现为南洋理工大学助理研究员的 Chaitanya Joshi 将为读者介绍图神经网络和 Transformer 之间的内在联系。具体而言，作者首先介绍 NLP 和 GNN 中模型架构的基本原理，使用公式和图片来加以联系，然后讨论怎样能够推动这方面的进步。

本文作者、南洋理工大学助理研究员 Chaitanya Joshi。

对「Transformer 是图神经网络」这一概念，这篇文章做了很好的解释。

首先，我们从表示学习开始。

NLP 中的表示学习

从一个很高的角度来看，所有的神经网路架构都是对输入数据的表示——以向量或嵌入矩阵的形式。这种方法将有用的统计或语义信息进行编码。这些隐表示可以被用来进行一些有用的任务，如图像分类或句子翻译。神经网络通过反馈（即损失函数）来构建更好的表示。

对于 NLP 来说，传统上，RNN 对每个词都会建立一个表示——使用序列的方式。例如，每个时间步一个词。从直观上来说，我们可以想象，一个 RNN 层是一个传送带。词汇以自回归的方式从左到右被处理。在结束的时候，我们可以得到每个词在句子中的隐藏特征，然后将这些特征输入到下一个 RNN 层中，或者用到任务中去。

从机器翻译开始，Transformer 就逐渐开始取代 RNN。这一模型有着新的表示学习策略。它不再使用递归，而是使用注意力机制对每个词构建表示——即每个词语在句子中的重要程度。知道了这一点，词的特征更新则是所有词的线性变换之和——通过其重要性进行加权。

Transformer 故障

通过将前一段翻译成数学符号以及向量的方式去创建对整个体系结构的认知。将长句 S 中的第 i 个单词的隐藏特征 h 从 ℓ 层更新至ℓ+1 层：

其中 j∈S 为句子中单词的集合，Q^ℓ、K^ℓ、V^ℓ为可学习的线性权重（分别表示注意力计算的 Query、Key 以及 Value）。针对句子中每个单词的并行执行注意力机制，从而在 one shot 中（在 RNNs 转换器上的另外一点，逐字地更新特征）获取它们的更新特征。

我们可通过以下途径更好地理解注意力机制：

考虑到 h_j^l； ∀j∈S 句中 h_i^l 和其他词的特征，通过点积计算每对（i，j）的注意力权重，然后在所有 j 上计算出 softmax。最后通过所有 h_j^l 的权重进行相应的加权，得到更新后的单词特征 h_i^l+1。

多头注意力机制

让点积注意力机制发挥作用是被证明较为棘手：糟糕的随机初始化可能会破坏学习过程的稳定性，此情况可以通过并行执行多头注意力将结果连接起来，从而克服这个问题（而每个「head」都有单独的可学习权重）：

其中 Q^k,ℓ、K^k,ℓ、V^k,ℓ是第 K 个注意力 head 的可学习权重，O^ℓ 是向下的投影，用以匹配 h_i^l+1 和 h_i^l 跨层的维度。

此外，多头允许注意力机制从本质上做「对冲」，从上一层看不同的转换或隐藏特征方面。

尺度问题和前向传播子层

一个推动 Transformer 的关键问题是词的特征在经过了注意力机制后可能会有不同的尺度： 1）这可能是因为在相加之后，有些词有非常高或分布注意力权重 w_ij； 2）在独立特征/向量输入阶段，将多个注意力头级联（每个注意力头都可能输出不同尺度的值），最终会导致最后的向量 h_i^ℓ+1 有不同的值。根据传统的 ML 思路，似乎增加一个归一化层是个合理的选择。

Transformer 克服了这一点，因为它使用了 LayerNorm，可以在特征层级归一和学习一个仿射变化。此外，Transformer 使用平方根来缩放点乘规模。

最终，Transformer 的作者还提出了另一个小窍门，用来控制尺度——一个有着特殊架构的、位置级别的双层全连接层。在多头注意力之后，它们会使用可学习权重来映射 h_i^ℓ+1 到一个更高维度。这其中使用了 ReLU 非线性，然后再将它映射会原有的维度，并使用另一个归一化操作。

Transformer 层的结构如下图所示：

在很多深度网络中，Transformer 架构是可以调整的，使得 NLP 社区可以从模型参数量和数据层面提升其规模。而残差连接也是堆栈 Transformer 层的关键。

GNN 构建图展示

图神经网络（GNNs）或图卷积网络（GCNs）在图形数据中建立节点和边的表示。通过邻域聚合（或者信息传递）来实现这一点，每一个节点从其相邻处收集特征，用以更新其相邻本地图结构的表示。堆叠多个 GNN 层能够使模型在整个图中传播每个节点的特征，从相邻处扩散到相邻处的相邻处，等等。

以社交网络为例： 由 GNN 产生的节点特征可以用于预测，比如识别最有影响力的成员或提供潜在的联系。

在最基本的形式中，GNNs 更新了第一层节点 i 的隐藏特征 h，并通过节点自身特征 h_i^l 的非线性转换添加到每个相邻节点 j∈N(i) 的特征 h_i^l 集合中：

其中 U^l,V^l 是 GNN 层的可学习矩阵，类似于 ReLU 的非线性矩阵。

领域 j 节点 j∈N(i) 上的和可以用其他输入大小不变的聚合函数来代替，如简单的均值/最大值或者是其他更有效的函数，比如通过注意机制得到的加权和。

如果我们采用邻域聚合的多个并行 head，用注意机制（即加权和）代替邻域 J 上的和，我们就得到了图注意网络（GAT）。添加正则化和前馈 MLP 就得到了 Graph Transformer。

句子就是全连接词语的图

为了让 Transformer 和图神经网络的关系更直接，我们可以将一个句子想象为一个全连接图，每个词都和其余的词相连接。现在，我们使用图神经网路来构建每个节点（词）的特征，这是之后可以在其他 NLP 任务中用到的。

广义来说，这其实就是 Transformer 所做的事情。它们实际上就是有着多头注意力（作为集群聚合函数： neighbourhood aggregation function）的 GNN。标准的 GNN 从局部集群节点 j∈N(i) 中聚合特征，而 Transformer 则将整个句子 S 视为一个局部集群，在每个层中从每个词 j∈S 获得聚合特征。

重要的是，各种针对问题的技巧，如位置编码、masked 聚合、规划学习率和额外的预训练——对于 Transformer 的成功很重要，但是很少在 GNN 中见到。同时，从 GNN 的角度来看 Transformer，可以帮助我们在架构上舍弃很多无用的部分。

可以从 Transformers 和 GNN 学到什么？

现在我们已经建立起了 Transformers 与 GNN 之间的联系，那么以下一些问题也就随之而来：

全连接图对于 NLP 来说是最佳的输入格式吗？

在统计型 NLP 和 ML 出现之前，诺姆·乔姆斯基等语言学家着重创建语言结构的形式化理论，如语法树/图等。 Tree-LSTM 就是其中一种尝试，但 Transformers 或者 GNN 架构是否能够更好地拉近语言学理论和统计型 NLP 呢？这又是一个问题。

如何学习长期依赖（long-term dependency）

全连接图的另一个问题是它们会使得学习单词之间的长期依赖变得困难。这仅仅取决于全连接图中的边数如何随着节点数而呈平方地扩展，例如在包含 n 个单词的句子中，Transformer 或者 GNN 将计算 n^2 个单词对。 n 数越大，计算愈加困难。

NLP 社区对于长序列和依赖的观点很有趣，即为了获得更好的 Transformers，我们可以在考虑输入大小的时候执行稀疏或自适应的注意力机制，在每一层添加递归或压缩，以及使用局部敏感哈希来实现有效注意力。

所以，融合 GNN 社区的一些观点有可能收获显著的效果，例如用于句子图稀疏化的二元分区（binary partitioning）似乎就是一个不错的方法。

Transformers 学习『神经句法』（neural syntax）吗？

NLP 社区已经有一些论文来探究 Transformers 学习什么的问题。但这需要一个基本前提，即执行句子中所有单词对的注意力（目的在于识别哪些单词对最有趣）使得 Transformers 能够学习到特定于任务的句法等。

此外，多头注意力中的不同 head 可能也关注不同的句法特征。

就图而言，在全图上使用 GNN 的情况下，我们是否能够基于 GNN 在每层执行临域聚合（neighbourbood aggregation）的方式来恢复最重要的边以及这些边的衍生？对此我并不确定。

为什么采用多头注意力？

我本人更赞同多头注意力机制的优化观点，因为拥有多注意力头能够增强学习效果，克服糟糕的随机初始化。例如，论文《Are Sixteen Heads Really Better than One?》中表明，在无重大性能影响的训练之后，Transformer 头可以被『剪枝』或『移除』。

多头邻域聚合机制也已证明在 GNN 中有效，例如 GAT 使用相同的多头注意力，论文《Geometric deep learning on graphs and manifolds using mixture model CNNs》中的 MoNet 使用多个高斯核（Gaussian Kernel）来聚合特征。尽管多头方法是用来实现注意力机制的平稳化，但这些方法是否能够成为发挥模型剩余性能的标准呢？

与之相反，具有和或最大值等更简单聚合功能的 GNN 不需要用多聚合头来实现平稳训练。所以，如果我们不计算句子中任意单词对之间的成对兼容性，它对 Transformers 不是更好的替代吗？

此外，完全摆脱注意力，Transformer 是否又会获益呢？ Yann Dauphin 等人所写的论文《Convolutional Sequence to Sequence Learning》提出了一个替代性的 ConvNet 架构。所以，Transformers 最终也可能会做出一些类似于 ConvNets 的改进。