谷歌图表征学习创新：学习单个节点多个嵌入&自动学习最优超参数

选自Googleblog

作者：Alessandro Epasto、Bryan Perozzi

机器之心编译

参与：高璇、shooting

将机器学习方法应用在图中并不容易，因为图大多是由离散部分组成的组合结构，而 ML 方法更喜欢连续结构。为了解决这一难题，谷歌引入了新的技术来学习单个节点的多个嵌入，并提出了一种自动学习最优超参数的方法。代码皆已开源。

表示实体间关系的关系数据在网络世界（如在线社交网络）和现实世界（如蛋白质交互网络（protein interaction network）中无处不在。这些数据可以表示为带有节点（如用户或蛋白质）和连接它们的边（如亲密关系或蛋白质交互）的图。

由于数据图的普遍流行，图分析在机器学习中发挥着重要作用，已应用于聚类、链接预测、隐私保护和其它方向。为了将机器学习方法应用于图（如预测新的亲密关系或发现未知的蛋白质交互），我们需要学习适合在 ML 算法中使用的图表征。

然而，图本质上是由诸如节点和边等离散部分组成的组合结构，而许多常见的 ML 方法（如神经网络）更喜欢连续结构，特别是向量表征。向量表征在神经网络中尤为重要，因为它们可以直接用作输入层。

为了解决在 ML 中使用离散图表征的难题，图嵌入方法学习图的连续向量空间，将图中每个节点（和/或边）分配到向量空间中的特定位置。这方面的一种流行方法是基于随机游走的表征学习。

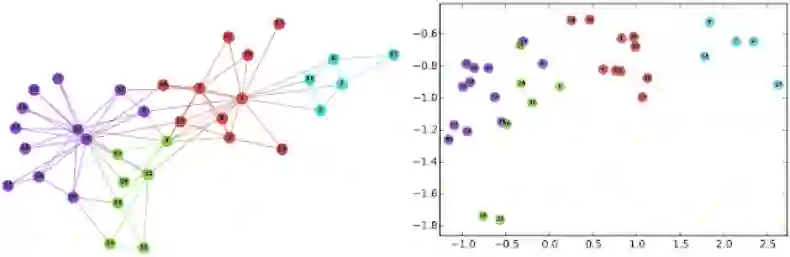
左图：代表社交网络的著名 Karate 图。右图：使用 DeepWalk 在图的连续空间嵌入节点。

这里有两篇关于图嵌入的论文：WWW 2019 的《Is a Single Embedding Enough? Learning Node Representations that Capture Multiple Social Contexts》和 NeurIPS 2018 的《Watch Your Step: Learning Node Embeddings via Graph Attention》。

 第一篇论文引入了一种新的技术来学习单个节点的多个嵌入，从而能够更好地描述具有重叠社区的网络。第二篇解决了图嵌入中超参数调整的基本问题，使人们可以轻松地部署图嵌入方法。谷歌已经在 github 上开源了这两篇论文的代码。

代码地址：https://github.com/google-research/google-research/tree/master/graph_embedding

捕获多个社交上下文的学习节点表征

基本上，标准图嵌入方法的关键假设是必须为每个节点学习单个嵌入。因此，嵌入方法的目标是识别表征图几何中每个节点的单个角色或位置。

然而，最近的研究发现，真实网络中的节点属于多个重叠的社区，并在其中扮演着多个角色。想想你的社交网络，你既隶属你的家庭，又隶属你的工作社区中。

这一观察引发了以下研究问题：是否有可能开发出将节点嵌入多个向量的方法，以代表它们参与了重叠的社区？

在论文《Is a Single Embedding Enough? Learning Node Representations that Capture Multiple Social Contexts》中，谷歌开发了 Splitter。这是一种无监督的嵌入方法，允许图中的节点具有多个嵌入，以便更好地编码它们在多个社区的参与。

该方法来自于最近的基于自我网络分析的重叠聚类中的创新理念，特别是使用角色图概念。该方法获取一个图 G，并创建一个新的图 P（称为角色图），其中 G 中的每个节点都由一系列称为角色节点的复制品表示。

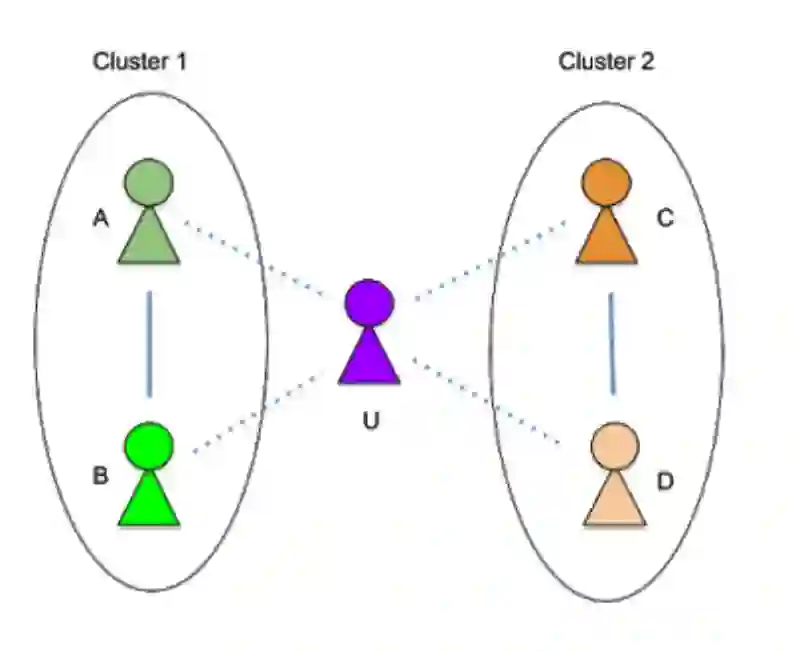
节点的每个角色代表了其所属的本地社区中节点的实例。对于图中的每个节点 U，分析节点的自我网络（即连接节点与其相邻节点的图，在本例中是 A、B、C、D），以发现节点所属的本地社区。

例如，在下图中，节点 U 属于两个社区：簇 1（与 U 的家人 A 和 B 一起）和 簇 2（与 U 的同事 C 和 D 一起）。

节点 U 的自我网络

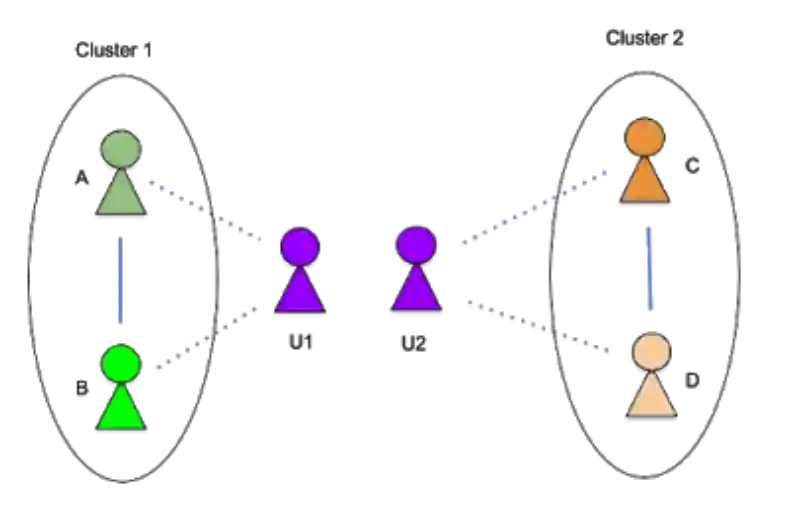
然后，使用这些信息将节点 U「分割」为两个角色 U1（家庭角色）和 U2（工作角色）。这将两个社区分离开来，使它们不再重叠。

自我分裂法将节点 U 分成 2 个角色

该技术已被用于改善图嵌入方法中的最新结果，结果显示在各种图上将链接预测（即预测将来将形成哪个连接）的误差减少了 90％。

这种改进的关键原因是该方法能够削减社交网络和其它现实世界图中的高度重叠。谷歌通过对作者属于重叠研究社区（如机器学习和数据挖掘）的合著图进行深入分析，进一步验证了这一结果。

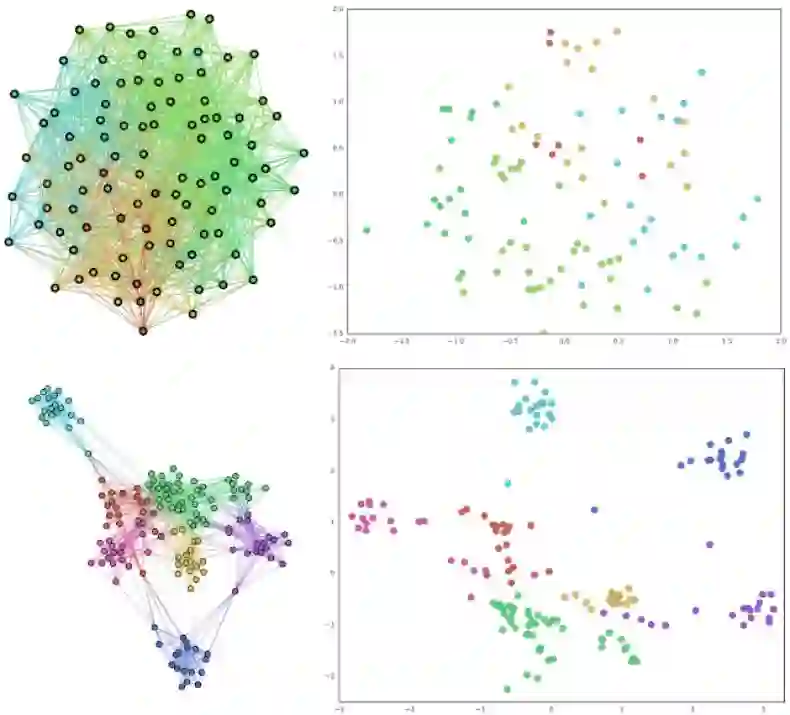
左上：具有高度重叠社区的典型图；右上：使用 node2vec 对左侧图实现的传统嵌入；左下：左上的角色图。右下：角色图的 Splitter 嵌入。请注意角色图如何清楚地分离原始图的重叠社区，以及 Splitter 输出分离好的嵌入。

通过图注意力机制自动进行超参数调整。

图嵌入方法在各种基于 ML 的应用程序（如链接预测和节点分类）上表现出色，但它们有许多必须手动设置的超参数。

例如，在学习嵌入时，捕获近节点比远节点更重要吗？即使专家可以微调这些超参数，但也需要单独调整每个图。

为了避免这种手工操作，在第二篇论文中，谷歌提出了一种自动学习最优超参数的方法。

具体来说，许多图嵌入方法（如 DeepWalk）都采用随机游走来探索给定节点周围的上下文（即直接相邻点、间接相邻点等）。这样的随机游走会产生许多超参数，这些超参数允许调整图形的局部搜索，从而调节嵌入到附近节点的注意力。

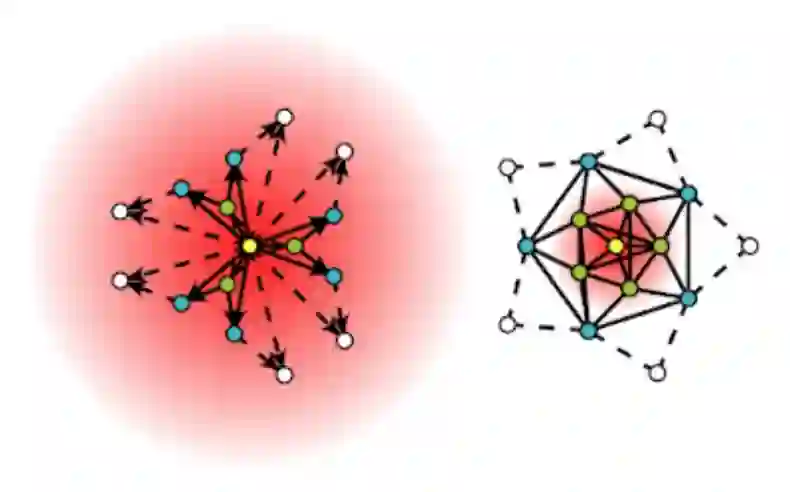
不同的图可能会呈现不同的最佳注意力模式，因此会呈现不同的最佳超参数（见下图，其中展示了两种不同的注意力分布）。

Watch Your Step 基于上述超参数为嵌入方法的性能制定了一个模型。然后谷歌使用标准反向传播优化超参数，以最大化模型预测的性能。结果发现反向传播所学习的值与通过网格搜索获得的最优超参数一致。

用于自动调整超参数的新方法——Watch Your Step 使用注意力模型来学习不同的图上下文分布。上面显示的两个示例是关于中心节点（黄色）的局部邻域以及模型学到的上下文分布（红色渐变）。左图显示了一个更分散的注意力模型，而右图分布显示了一个集中在直接邻近节点上的模型。

这项工作属于日益壮大的 AutoML 家族，谷歌希望能够减轻优化超参数的负担，毕竟优化超参数是实际机器学习中的常见问题。

许多 AutoML 方法都使用神经架构搜索。但本文使用了一种变体，使用了嵌入中的超参数和图论矩阵公式之间的数学联系。「自动」部分即通过反向传播学习图超参数。

谷歌希望自己的贡献将进一步推动图嵌入研究各个方向的发展。其用于学习多节点嵌入的方法将丰富并深入研究的重叠社区检测领域与最近的图嵌入联系在一起。该领域一个悬而未决的问题是使用多嵌入方法进行分类。

此外，谷歌对学习超参数的贡献在于通过减少高昂的手动调参需求来促进图嵌入的应用。希望这些论文和代码的发布将有助于研究界更致力于这些方向。

原文链接：https://ai.googleblog.com/2019/06/innovations-in-graph-representation.html

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者 / 实习生）：hr@jiqizhixin.com

投稿或寻求报道：content@jiqizhixin.com

广告 & 商务合作：bd@jiqizhixin.com