红包统计学：为何有些人盆钵满盈，有些人入不敷出？

会员服务 ·

红包统计学：为何有些人盆钵满盈，有些人入不敷出？

2018 年 8 月 5 日 算法与数学之美

如果你有一台智能手机，如果你在上面装了某个软件，那么你今年的春节很可能是在下面这样的场景中度过的：

这也使得众多的网友发出了下面的感慨：

而最近不少群里面又流行起来一种“红包接力”的玩法，大概的规则是：群里面先由一人发一个红包，然后大家开始抢，其中金额最大的那个人继续发新一轮的红包，之后不断往复循环。

这时候大家或许就会问了，一直这么玩下去会有什么结果呢？是“闷声赚大钱”了，还是“错过几个亿”了？是最终实现“共同富裕”了，还是变成“寡头垄断”了？要回答这些问题，我们不妨用统计模拟的方法来做一些随机实验，得到的结果或许会让你大跌眼镜呢。

红包初级模型——切面条法

要进行模拟实验，就需要设定一个红包金额的分配机制。但由于微信红包的算法并没有公开，所以我们只好从观察到的现象出发，“反推”出一个模型，让它尽量符合观察结果。其实这就是科学方法的精髓：我们也许永远不可能知道宇宙的“源代码”，但我们能为宇宙建立一个足够好用的模型。

微信的红包是一个个抢的，所以很容易给人以这样的印象：红包一堆钱摆在那里，第一个人闭眼抓一把，第二个人再抓一把，等等。但是倘若果真如此，后来的人总体而言就要吃亏。这样既不公平，也不满足现实中的观察。

所以，更合理的做法是，一开始就把所有的钱一次性分成几个包，每人抓一个，每个包都是等同的，里面的钱数期望都是总金额的几分之一。满足这个要求的做法当然不止一个，但我们先考虑最符合直觉的办法——切面条。

假如你有一根面条要随机分成5根，怎么分？闭上眼睛剁4刀就行了。换成数学语言，就是在一条线段上随机扔4个点，分成5段。

现在你要把红包分成5份，好办，拿出你刚才剁的面条，每一根面条有多长，对应的红包就塞多少钱。

（当然，面条是连续的，而红包是离散的——每个包的钱数都是1分钱的整数倍。但钱多的时候这点差异无关紧要，而要是有人发了个全一分钱的红包，还是暂停讨论把他踢出群比较好。）

以下就是切面条法分红包的一个实例，总金额为1元，分成5个：

0.02669467， 0.248426309，0.23745777，0.35864430，0.12877695

这贫富差距也太大了吧？如果红包总金额是100，那么领得最多的人可以得到35.86元，而最少的只有2.67元。第一名得到三分之一多的钱，最后一名不到三十分之一？其实这完全不极端。对于这种分法，我们可以数学上证明，当1块钱（或者长度为1的面条）分成n份儿的时候，

第k大的值，期望为1/n*(1/n+1/(n-1)+1/(n-2)+…+1/k)。（证明留作练习（被踢飞））

所以，最大值的期望为 1/n*(1/n+1/(n-1)+1/(n-2)+…+1)，

而最小值的期望为 1/n^2。

换言之，在n=5的时候，平均而言，五个人应该分别拿到的红包大小是：0.456666……，0.256666……，0.156666……，0.09，0.04。真是朱门酒肉臭路有冻死骨啊。

好吧，虽然这恐怕和很多人的印象相符，但毕竟也太悬殊了，能不能增加一个调节杆，让红包间的差异稍微小一点呢？

红包进阶模型——狄利克雷分布

复习一下刚才的切面条模型要点。

1 一次可以生成n个随机数，且总和为1，这样每个数乘以红包总金额就是每个人分得的钱；

2 每个随机数的期望应该均等，即n分之一，这是为了保证大家抢红包机会平等；

现在我们为它增加一个第三条：

3 有一个参数可以用来调节红包的“公平”程度。这里的公平不是指机会公平，而是说每次发红包大家实际拿到手的钱是不是相近，即金额分配的波动性是大还是小。比如100元的红包发给10个人，如果每人都是10元左右，我们认为这种分配更公平些；如果最少的才0.8元，最多的有20元，显然就有失公允了（不幸的是作者好几次碰到这种情况……）。

幸运的是，在众多的随机变量分布中，有一个“狄利克雷分布”非常适合上面列出的这些情况。狄利克雷分布本身有n个参数，但为了满足条件2，我们可以只用一个参数 α 来决定它的具体形式。α 越大，每人分得的金额比例就越倾向于平均，反之则波动性越大。

更幸运的是，我们开始提出的切面条分法，恰恰就是当α=1的时候，狄利克雷分布的最简单状态。

刚才切面条的结果，也就是α=1时的狄利克雷分布生成的随机数

0.02669467， 0.248426309，0.23745777，0.35864430，0.12877695

而下面是α=10时的一组随机数

0.2459250，0.2722147，0.1717301，0.1398133，0.1703169

可以看出，当α=1时，金额分配的变动性非常大，而在α=10的情形下，金额的分配就平均多了。

模拟接力游戏，开始

有了这个假想的红包分配机制，我们就可以来模拟红包接力的游戏。首先假设我们有一个50人的群，每人初始手头上的可用金额为50元（这里是为了产生“破产”现象而故意放低的，土豪们请忽略此设定），根据规则，每次红包的总金额是20元，发放给10个人，其中抢得最大红包金额的人将发出下一轮的红包。如果某人发完红包后余额变成了负值，就不能再继续抢红包（请原谅这个丧心病狂的设定……），因为他/她已经发不起下轮红包了，但允许现在其余额为负。

在我们的模拟中，依然对实际情况做了很多简化，比如假设抢到红包的人是在参与游戏的人中间均匀分布的（排除了资产为负的人）。在实际情况中，大家可能会根据自己余额的多少来决定是否继续参加，但在此我们忽略了这种可能。

我们设定 α=2，并让红包接力100次，最后大家的余额如下：

31.24 82.69 18.07 44.56 62.87 33.40 47.00 45.55 77.11 70.44

54.28 26.98 54.74 80.30 28.32 43.98 48.80 82.69 82.94 -11.00

34.30 80.64 60.68 47.34 40.13 52.55 23.39 62.67 92.20 72.43

41.55 40.12 50.51 81.30 51.17 43.36 34.93 64.38 42.70 -8.90

9.10 78.61 46.35 64.18 61.90 13.61 50.01 68.51 41.21 54.14

可以看出，有两位朋友不幸破产了，而最后资产最多的有92.20元，几乎翻了一倍。一个很明显的事实是，破产的玩家都是因为“中头奖”中得太多了，导致入不敷出。相反，最终收得92.20元的这位玩家属于“闷声发大财”。经统计，他/她获得第一名0次，第二名3次，第三名2次，第四名2次，第五名4次，等等。

下面这个flash展示了每个人的金钱变动状况：

当然，概率面前人人平等，没有谁能预知自己抽中红包后会是最大的还是最小的，所以从对称性的角度考虑，个人选择的结果是完全随机的。但是，从整个群的角度来看，有一个指标却在悄悄发生变化，那就是这个群的“贫富差距”。

平均还是独大？基尼系数来判断

我们注意到，在游戏最开始的时候，大家的资金都是一样的（50元），而在100次接力之后，几家欢喜几家愁，贫富差距被拉大了。于是我们有两个很自然的问题：1. 如何量化这种贫富差距？2. 随着游戏的进程，贫富差距会有怎样的变化？

对于第一个问题，我们可以借用经济学中的一个概念来予以回答，那就是所谓的“基尼系数”（Gini Coefficient）。基尼系数通常被用来衡量一个国家居民收入的公平性，其取值在0到1之间，越大表示贫富差距越大，即少部分的人掌握了这个经济体大部分的收入。基尼系数的计算公式可以在它的维基页面中找到，对于之前的模拟游戏结果，计算出的基尼系数是0.2551。

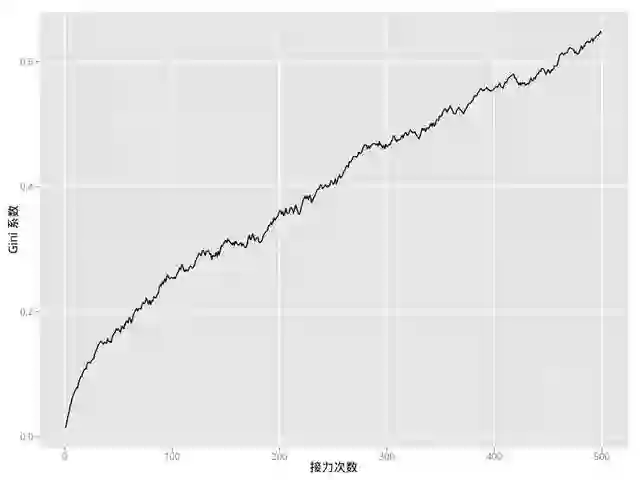
这个结果的绝对数值可能并没有太大的意义，因此我们在每一轮接力之后都计算出当时这个群的基尼系数，然后观察它的变化。结果如下：

在这里我们将接力次数延长到了500次。可以看出，随着接力的进行，基尼系数的整体趋势是在不断变大的，意味着贫富差距会随着游戏的进行变得越来越大。这其实很好理解：总是会有人因为拿了太多头奖而破产，这样财富会在越来越少的人中间进行分配，所以相应地贫富差距就拉大了。

红包越“公平”，贫富差越大

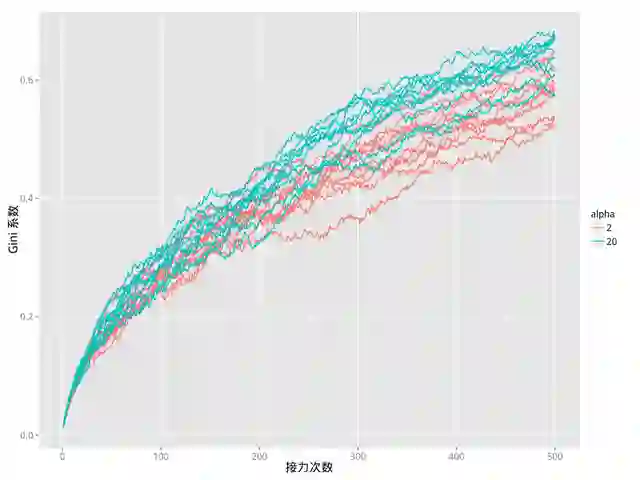
前面提到，在我们的模型中有一个参数 α 用来控制红包金额分配的“公平”程度（或者更准确地说，是“平均”的程度，因为就机会而言，每个人分得金额的可能性都是相同的，但就每一次实际分得的金额而言，α 越大，这种分配越倾向于平均，即结果的波动性越小）。下图展示了一组随机模拟实验的结果，其中我们模拟了20次红包接力的游戏，10次取 α=2，另外10次取 α=20。每次游戏中，红包都接力了500次。

可以看出，红线和蓝线虽然有所重叠，但总体来看蓝线的取值要比红线更大，也就是说，红包金额越“公平”，贫富差距反而会越大。

这个结论看起来可能有些反直觉，但其实也合情合理：如果红包的分配是绝对公平的，那么第一名得到的金额就将是2元，而下一轮又必须送出20元，所以总共亏损18元；如果红包金额的波动性很大，就会有一部分人得到的金额小于2元，而第一名就会得到更多，也就更不容易破产。所以说，一个规则是否真的“公平”，不能只看其表面。

出人意料的更多玩法

除了前面提到的这个规则，我们还可以考虑一系列其他的玩法：

1. 之前的规则记为1号；

2. 玩法2：第一个红包金额为20，第二个为21，第三个为22，……到30后又递减至20，以此反复；

3. 玩法3：下一个红包的总金额是上一轮的最大金额加10；

4. 玩法4：下一个红包的总金额是上一轮最大金额的4倍，30封顶；

5. 玩法5：下一个红包的总金额是上一轮最大金额的5倍，30封顶；

你一定奇怪玩法4和玩法5只差一个数，为什么要单独列出来。这里可以先剧透一下，原因是它们有着天壤之别。在给出结果之前，大家可以先根据自己的直觉给这几种玩法排个序，然后再和下面的结果对比一下，看看是否真的让你大跌眼镜了。

3

2

1

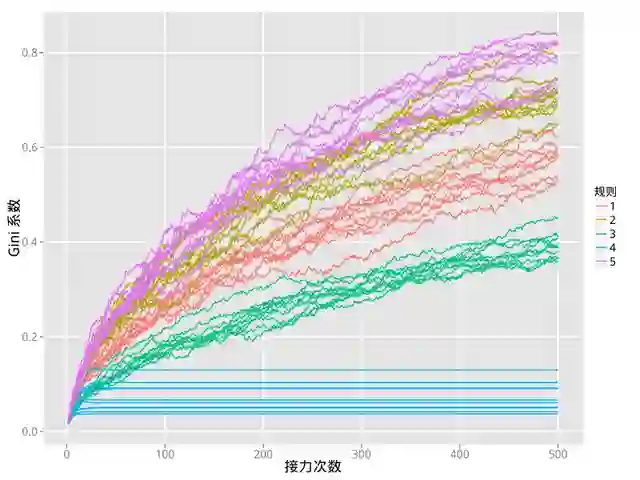
下面是这五种玩法的对比图，全部取10个红包，α=2，初始20元。每种玩法我们模拟10次，也就是有10条基尼系数曲线。

可以看出，按照贫富差距排序，从大到小分别是玩法5>玩法2>玩法1>玩法3>玩法4。怎么样，你猜对了吗？

我相信你一定被4和5之间的“天壤之别”惊呆了。为什么一个是最大，而另一个甚至是平坦的呢？

其实，规则里面4和5这两个系数非常关键。在α=2、分10个包的条件下，第一名平均能拿到红包金额的23%左右。4乘以23%得到0.92<1，换言之红包会变得越来越小。比如第一轮最大如果是4，下一轮的总金额就是16；这一轮最大可能就变成了3，那么再下一轮总金额就变成了12……到了后来，总金额小于1分钱，就保持不变了（图中的水平线部分）。相比之下，5乘以23%得到115%，结果红包会变得越来越大，而由于我们设定了30块钱封顶，会让每个红包稳定在30元附近，因此贫富差距就按照“正常”的趋势逐渐加大了。

可以想见的是，在4倍和5倍之间应该会有一个临界值，把这两种极端情形分隔开来。时间所限我们没有进行严谨的理论推演，但随机模拟表明这个数字在4.35左右。

最后的话

正如开篇所言，这只是红包算法的一个模型，并不一定就是背后的真实源代码。从经验和直觉上来看，这个模型（特别是在α较小时）对现实的模拟还算令人满意，不过严格的科学方法当然要做统计分析来验证这一模型是否符合现实了——鉴于验证繁琐，红包数据收集不易，而且本身就是个娱乐项目，此处就不再对此较真。欢迎感兴趣的读者进行更深入的验证。

除了本文考察的这些可能影响金额分配的因素之外，读者还可以利用文中用到的代码继续考察其他因素对贫富差距的影响（可能需要对代码稍作修改），比如红包人数，初始金额等等。

最后提醒大家的是，红包主要还是在过年的时候图个喜庆，游戏有风险，抢包需谨慎。:D

Via:果壳网

附：文本用到的R预言代码

rdir = function(n, shape){    len = length(shape)    mat = matrix(rgamma(len * n, shape), len)    sums = colSums(mat)    t(mat) / sums}gini = function(x) {    x = sort(x)    n = length(x)    2 * sum(seq_along(x) * x) / n / sum(x) - (n + 1) / n }param = list(group_size = 50,    ## 群大小             init_balance = 50,  ## 每人初始金额             hb_amount = 20，    ## 每次红包的总金额             hb_size = 10,       ## 红包发给多少人             niter = 100，       ## 红包接力次数             alpha = 2           ## 红包金额分配参数             ) hb_experiment = function(p) {    id = 1:p$group_size  ## 群成员 ID 编号    balance = rep(p$init_balance, p$group_size)  ## 当前每人资产        bal = matrix(0, p$niter, p$group_size)    for(i in 1:p$niter)    {        ## 破产的就别再玩啦        players = id[balance > 0]        if(i == 1)        {            ## 第一轮随机挑一个人发红包            host = sample(players, 1)        } else {            ## 后面就找抢得最多的            host = winners[which.max(winner_amount)]        }        ## 红包主掏钱        balance[host] = balance[host] - p$hb_amount        ## 手快有，手慢无        winners = sample(players, p$hb_size)        ## 每人领取的红包金额        winner_amount = p$hb_amount * c(rdir(1, rep(p$alpha, p$hb_size)))        balance[winners] = balance[winners] + winner_amount        bal[i, ] = balance    }    return(list(balance = bal, last_balance = balance)) }set.seed(123) b = hb_experiment(param)$last_balance gini(b)