ICLR 2018最佳论文：AMSGrad能够取代Adam吗

2018 年 4 月 22 日 全球人工智能 F. Korzeniowski

作者：Filip Korzeniowski

编译：weakish

编者按：Google的Reddi等关于Adam收敛性的论文最近被评为ICLR 2018最佳论文，其中提出了一个Adam的变体AMSGrad。那么，在实践中，AMSGrad是不是能够取代Adam（目前深度学习中最流行的优化方法之一）呢？让我们一起来看奥地利林茨大学（JKU）博士Filip Korzeniowski所做的试验。

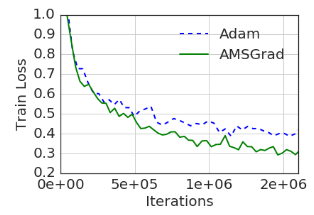
在ICLR 2018最佳论文On the Convergence of Adam and Beyond（关于Adam的收敛性及其他）中，Google的Reddi等指出了Adam收敛性证明的缺陷，并提出了一个Adam算法的变体AMSGrad。论文通过一个合成任务和少量试验展示了AMSGrad的优势。然而，它仅仅使用了小型网络（MNIST上的单层MLP，CIFAR-10上的小型卷积网络），并且没有表明测试精确度（显然，比起交叉熵损失，我们更加关心精确度）。从训练和测试损失上看，他们在CIFAR-10上训练的卷积网络，比当前最先进的结果要差很多（我们并不知道精确度）。

由于我一般习惯使用Adam，所以我决定在更实际的网络上评估一下AMSGrad。请注意，我这里训练的模型也不大，也不是当前最先进的，但绝对比论文展示的更实际。

我在Lasagne的Adam实现的基础上做了修改，实现了AMSGrad。我还添加了一个关闭Adam的偏置纠正（bias correction）的选项。

  
    
    
    
   
     
     
     def amsgrad(loss_or_grads, params, learning_rate=0.001, beta1=0.9,
   
     
     
                 beta2=0.999, epsilon=1e-8, bias_correction=True):
   
     
     
         all_grads = get_or_compute_grads(loss_or_grads, params)
   
     
     
         t_prev = theano.shared(utils.floatX(0.))
   
     
     
         updates = OrderedDict()
   
     
     
     
   
     
     
         # 使用theano常量以避免向上转型（upcast）到float32
   
     
     
         one = T.constant(1)
   
     
     
     
   
     
     
         t = t_prev + 1
   
     
     
     
   
     
     
         if bias_correction:
   
     
     
             a_t = learning_rate*T.sqrt(one-beta2**t)/(one-beta1**t)
   
     
     
         else:
   
     
     
             a_t = learning_rate
   
     
     
     
   
     
     
         for param, g_t in zip(params, all_grads):
   
     
     
             value = param.get_value(borrow=True)
   
     
     
     
   
     
     
             m_prev = theano.shared(np.zeros(value.shape, dtype=value.dtype), 
   
     
     
                                    broadcastable=param.broadcastable)
   
     
     
             v_prev = theano.shared(np.zeros(value.shape, dtype=value.dtype), 
   
     
     
                                    broadcastable=param.broadcastable)
   
     
     
             v_hat_prev = theano.shared(np.zeros(value.shape, dtype=value.dtype), 
   
     
     
                                        broadcastable=param.broadcastable)
   
     
     
     
   
     
     
             m_t = beta1*m_prev + (one-beta1)*g_t
   
     
     
             v_t = beta2*v_prev + (one-beta2)*g_t**2
   
     
     
             v_hat_t = T.maximum(v_hat_prev, v_t)
   
     
     
             step = a_t*m_t/(T.sqrt(v_hat_t) + epsilon)
   
     
     
     
   
     
     
             updates[m_prev] = m_t
   
     
     
             updates[v_prev] = v_t
   
     
     
             updates[v_hat_prev] = v_hat_t
   
     
     
             updates[param] = param - step
   
     
     
     
   
     
     
         updates[t_prev] = t
   
     
     
         return updates

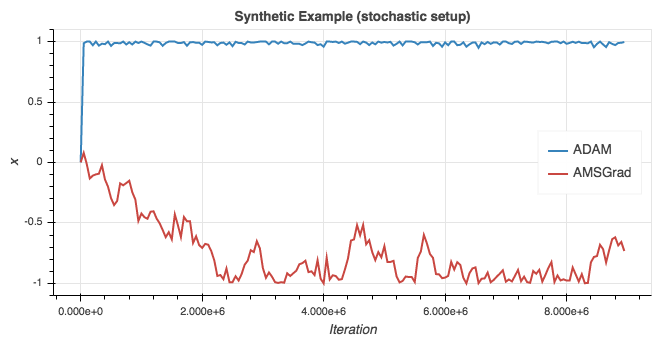
首先，让我们检查下实现是否正确。我运行了论文中概述的合成试验（使用随机配置）。下图为所得学习曲线。

这和论文中的图形相当接近了，也和ycmario的重新实现的结果差不多。Adam错误地收敛于1，而x的最佳值为-1.

我接着试验了四种配置：

MNIST上的逻辑回归。
CIFAR-10上的CifarNet（论文中描述的CNN）。
CIFAR-10上的SmallVgg（一个小型的VGG风格网络）
CIFAR-10上的Vgg（一个较大的VGG风格网络）

在每种配置中，我为所有下列组合各运行了5遍训练：

beta2 ∈ {0.99, 0.999} （据论文建议）
学习率 ∈ {0.01, 0.001, 0.0001}
偏置纠正 ∈ {on, off}

batch大小为128（和原论文一样）。训练了150个epoch，初始学习率线性下降，直到在第150个epoch后降至0. 在CIFAR-10试验中，我同样使用了标准的左右翻转数据增强。相应的代码见GitHub仓库fdlm/amsgrad_experiments。

让我们首先关注Vgg配置。虽然这些配置各有其古怪之处，我们可以从结果得出的结论却是类似的。

CIFAR-10上的Vgg

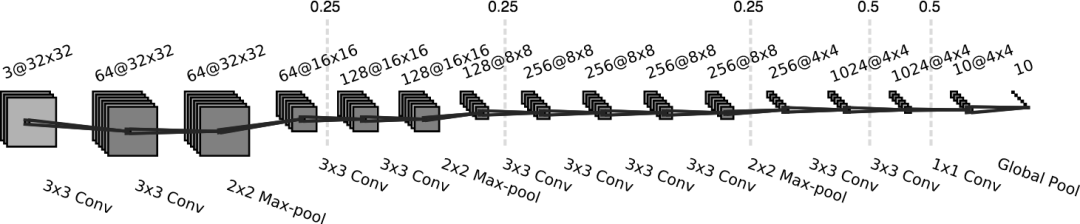
我这里使用的卷积网络结构如下：

每层卷积之后是batch normalisation和rectifier激活函数。虚线标志着dropout，相应的概率标明在线的上方。细节详见代码。

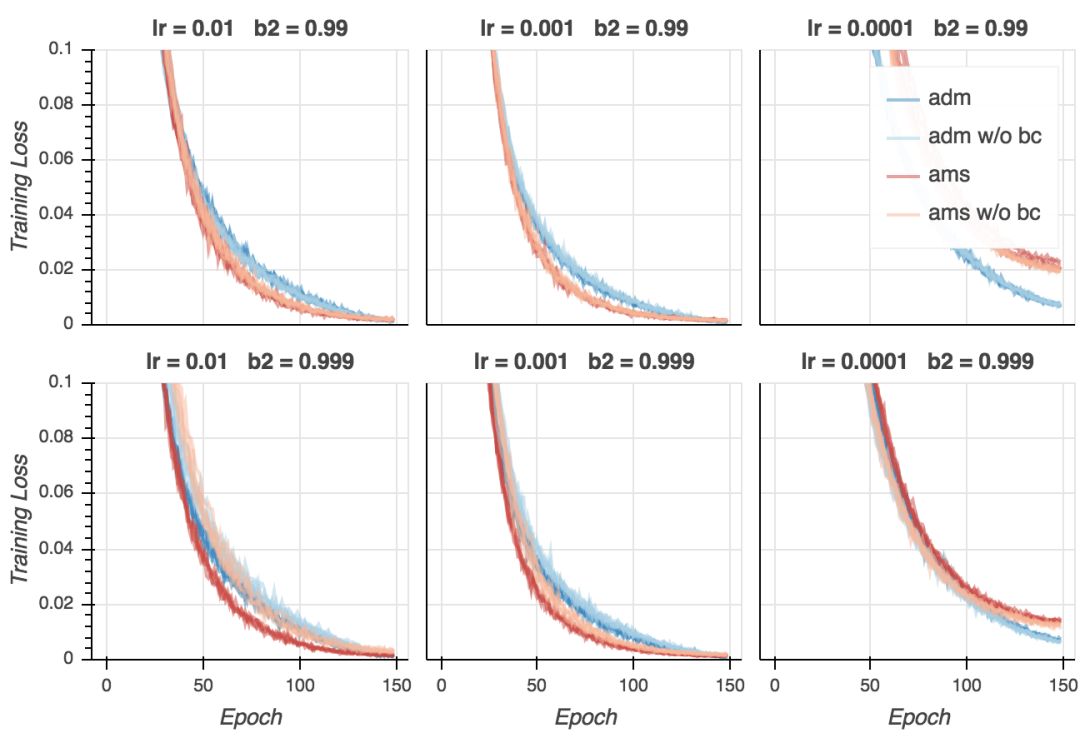
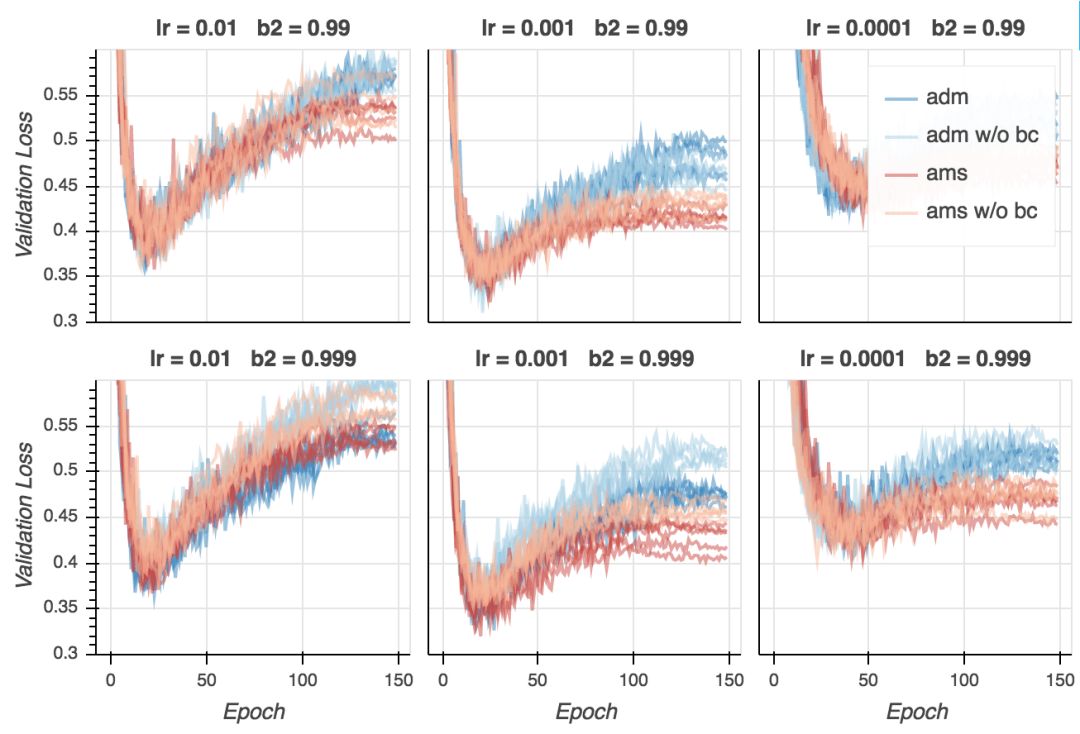
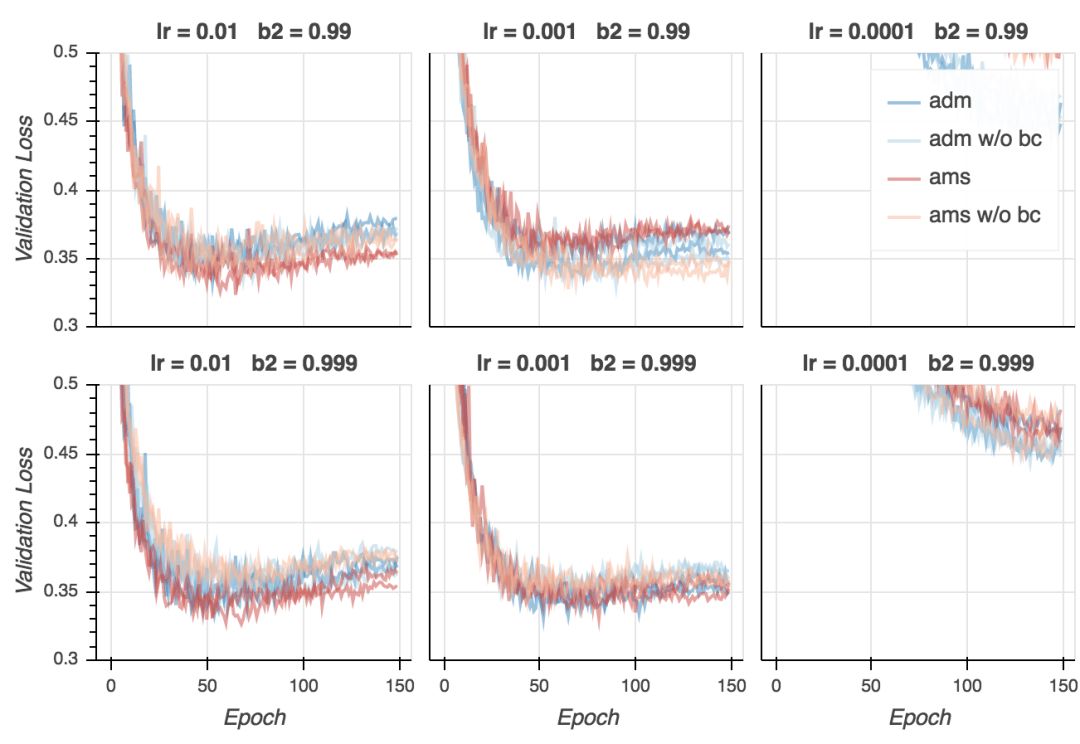
在下面的图形中，Adam的结果用蓝色表示，AMSGrad的结果用红色表示。较淡的颜色表明偏置纠正关闭了。每条线表示一次训练。

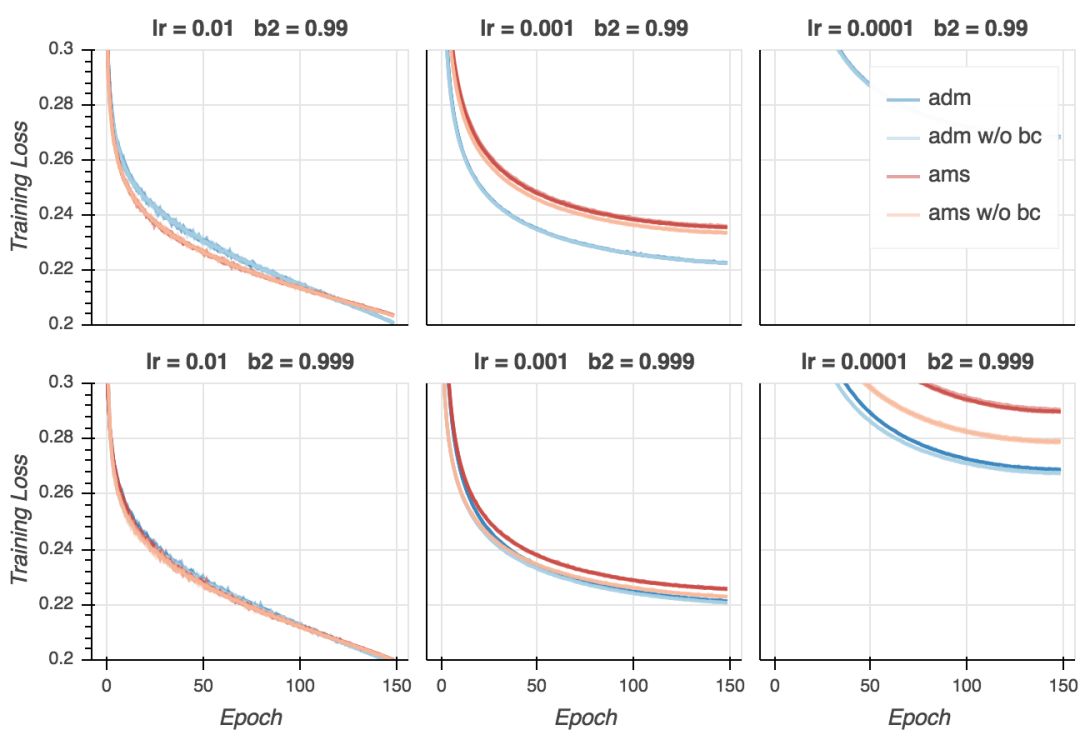
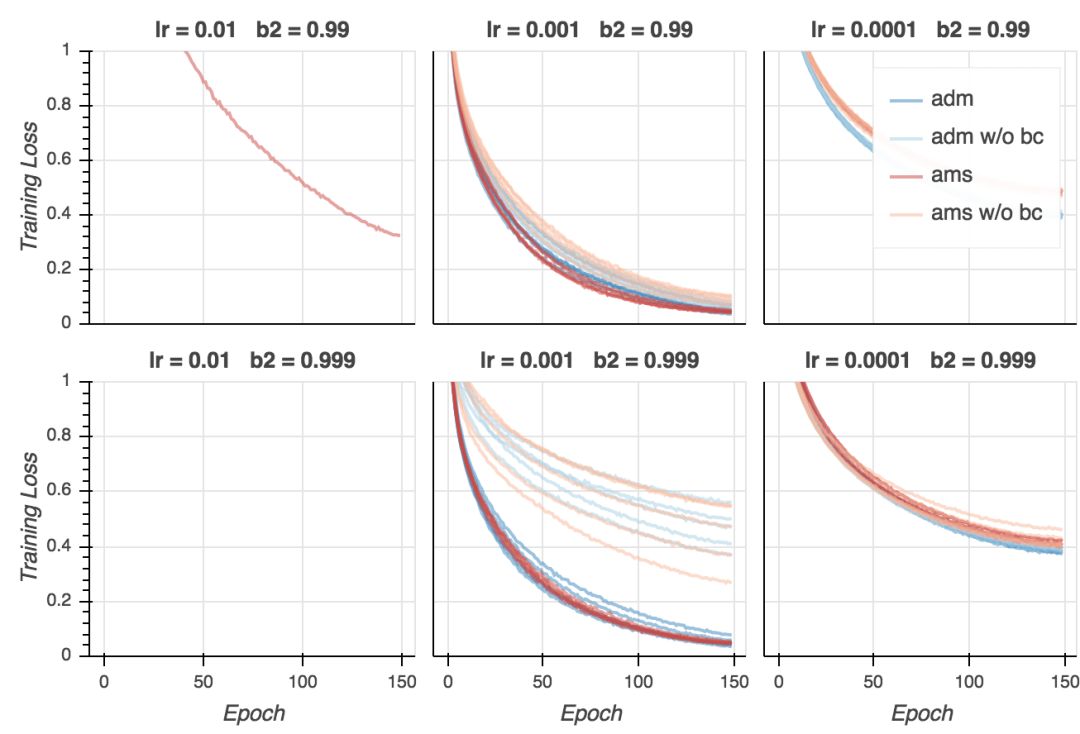
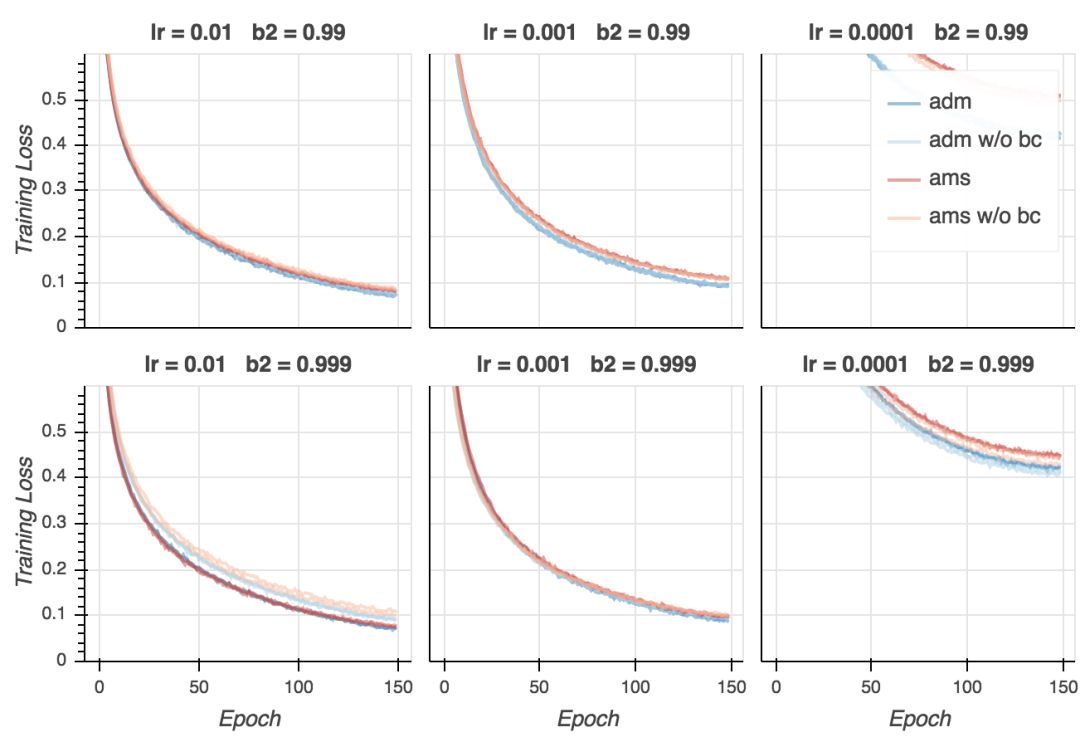
训练损失

在我的试验中，训练损失非常接近0，而论文中的数值则是0.3. 这当然是因为我用的是大得多的模型。我们同时看到，如果学习率不是太低的话，AMSGrad看起来在最后的训练阶段收敛得快一点，并且大多数情况下，使用偏置纠正有助于收敛。不过，最后所有变体在大多数超参数配置下（学习率过低除外）收敛至相似的最终损失。如果我们仔细查看，我们会发现在最后的若干epoch上Adam超越了AMSGrad。这没什么大不了的——毕竟这是训练损失。然而，这类模型（以及训练方案）和论文中报告的CifarNet模型的结果很不一样，论文中的情况是，AMSGrad的训练损失比Adam低很多。

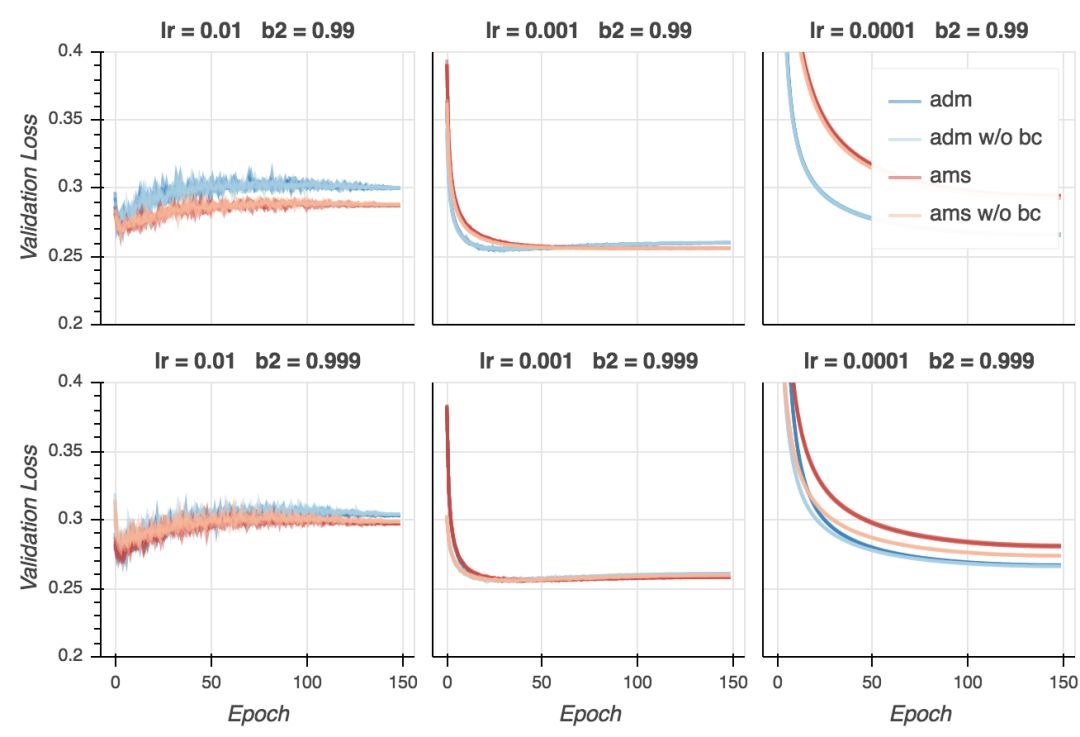
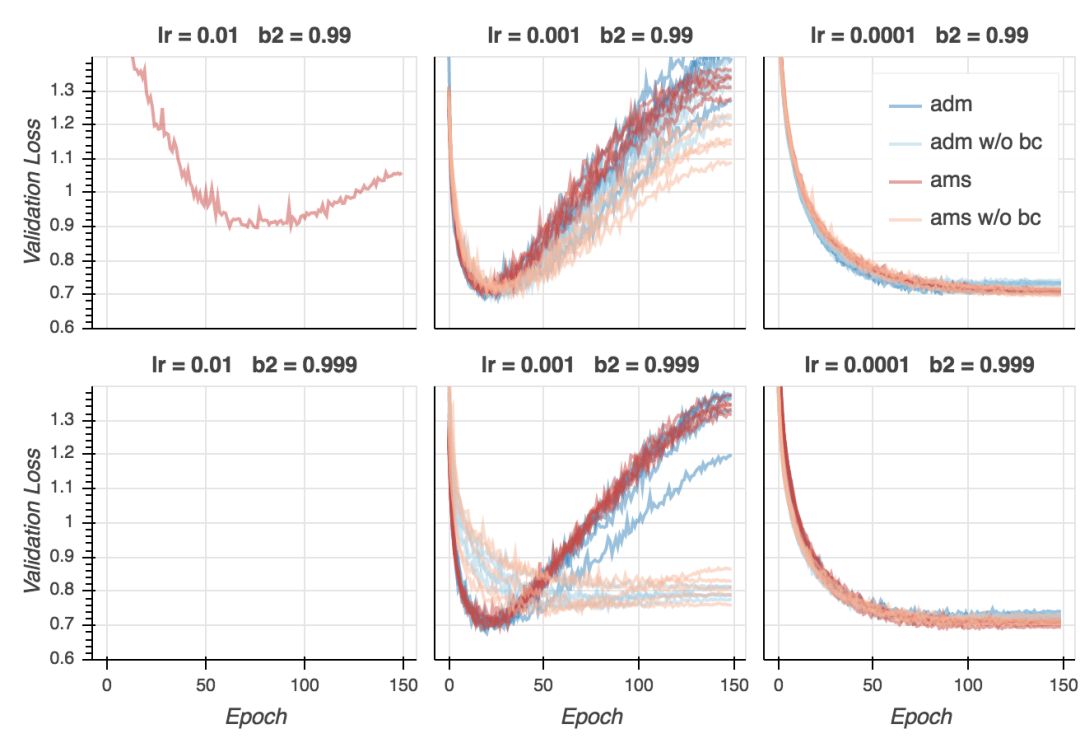
验证损失

验证损失的表现不同。我们看到，AMSGrad持续超越Adam，特别是在后期的epoch中。两个算法达到了相似的最小验证误差（在第20-25个epoch周围），但自此之后，Adam看起来过拟合地更厉害，至少是就交叉熵损失而言。所以AMSGrad可以弥补Adam经常比标准SGD（随机梯度下降）概括性差这一点吗？需要做一些标准SGD的试验来回答这一问题。

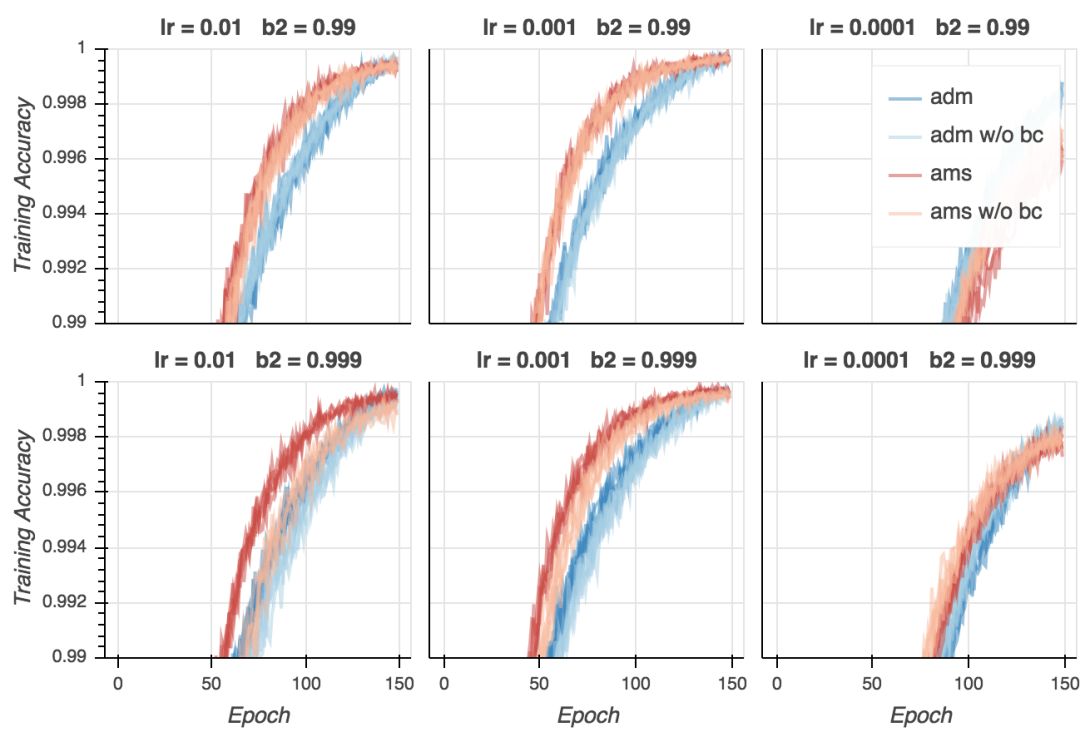
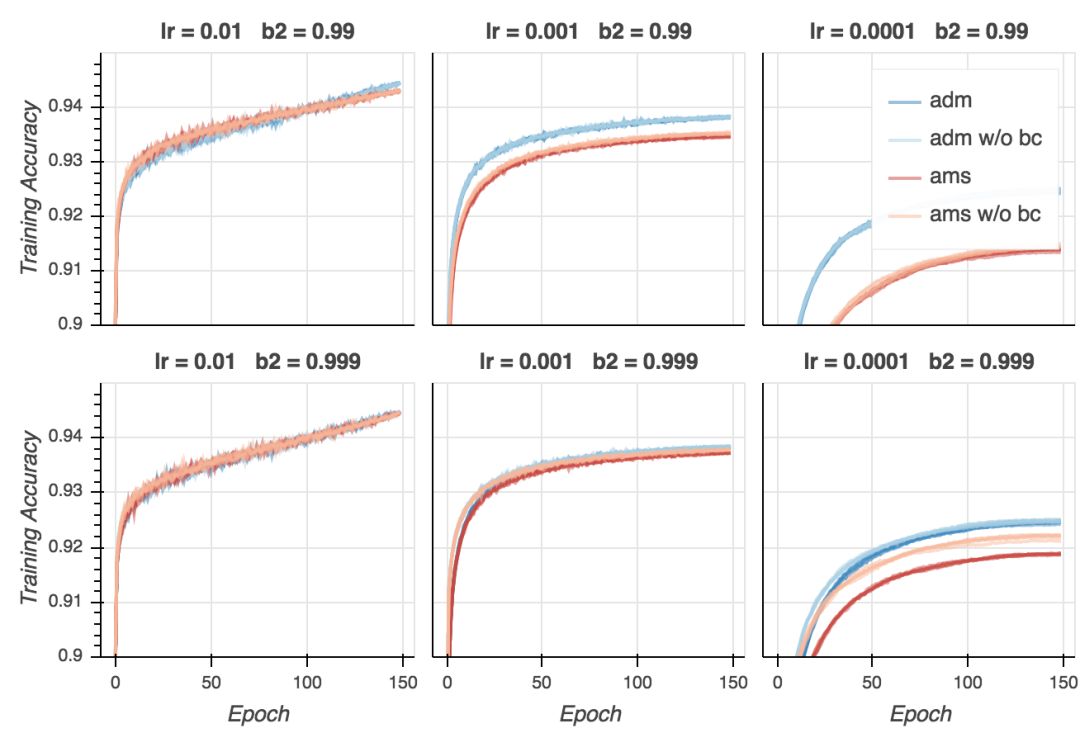
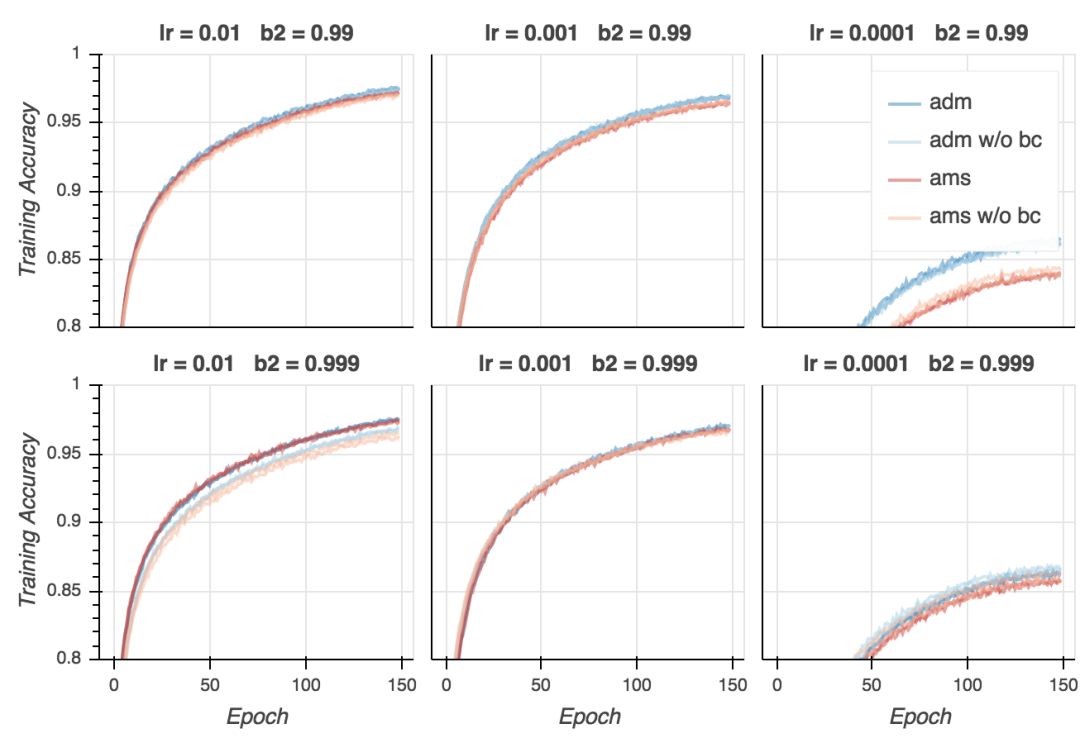
训练精确度

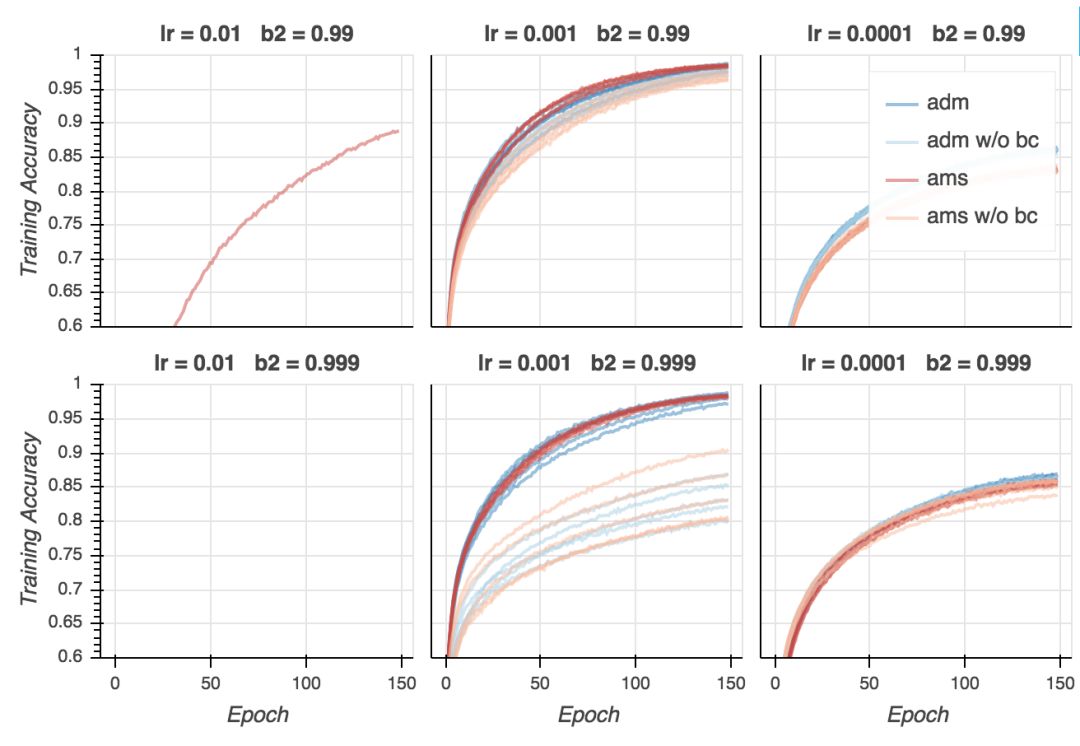
让我们看下精确度。在分类问题中，精确度是一个比交叉熵损失重要得多的量度。毕竟，我们在乎的是我们的模型成功分类了多少样本。首先，让我们看下训练精确度。就CIFAR-10而言，大部分强大的模型能够达到接近100%的精确度，如果训练是恰当的话（事实上，即使使用随机标签，它们仍能达到100%精确度。）

正如我们看到的，训练精确度和训练损失的表现差不多：AMSGrad比Adam收敛得快，但最终的结果差不多。如果超参数不是太离谱的话，不管使用哪种算法，我们都能达到差不多100%的精确度（同样，学习率不能太低）。

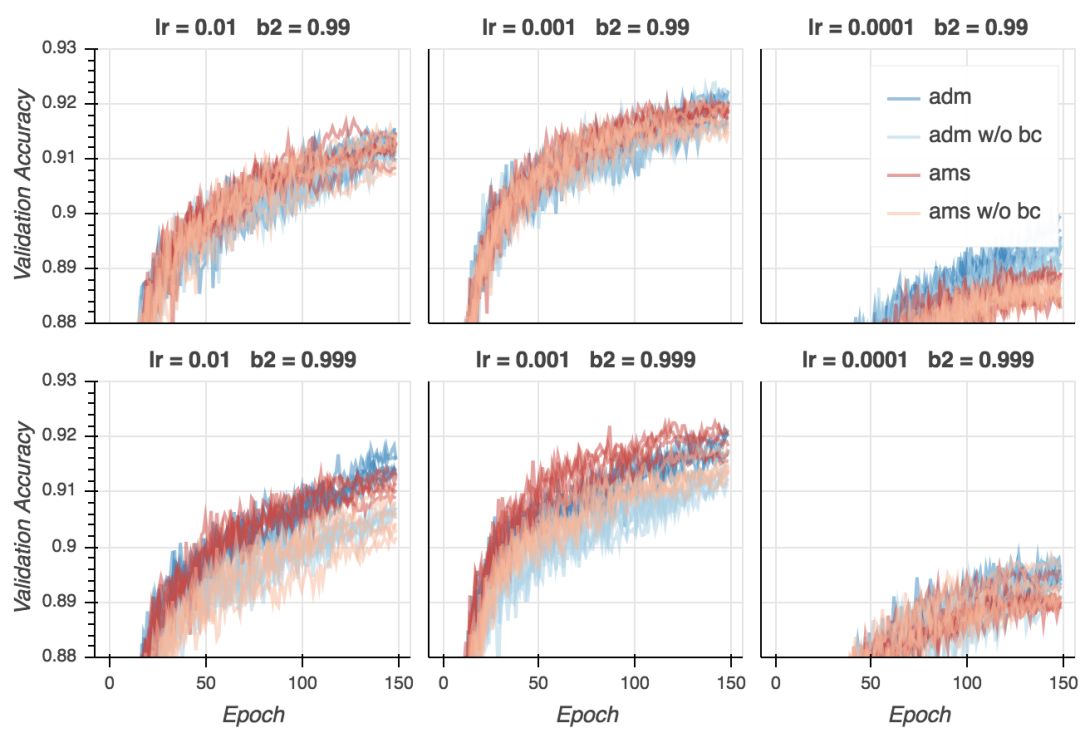
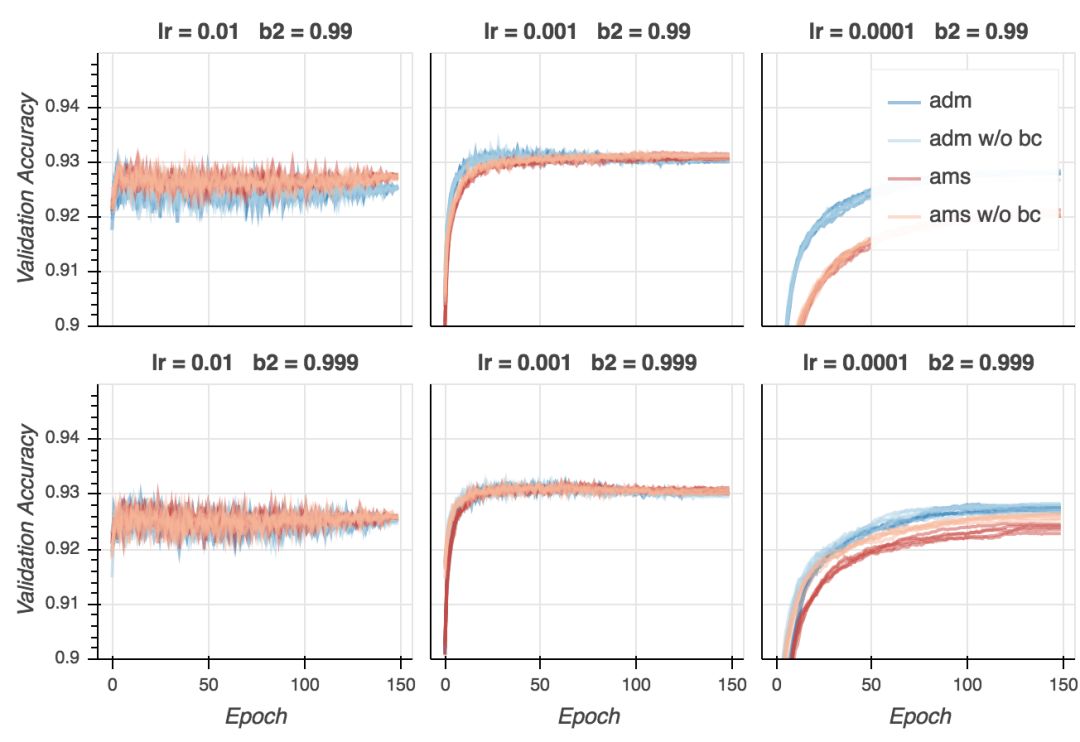
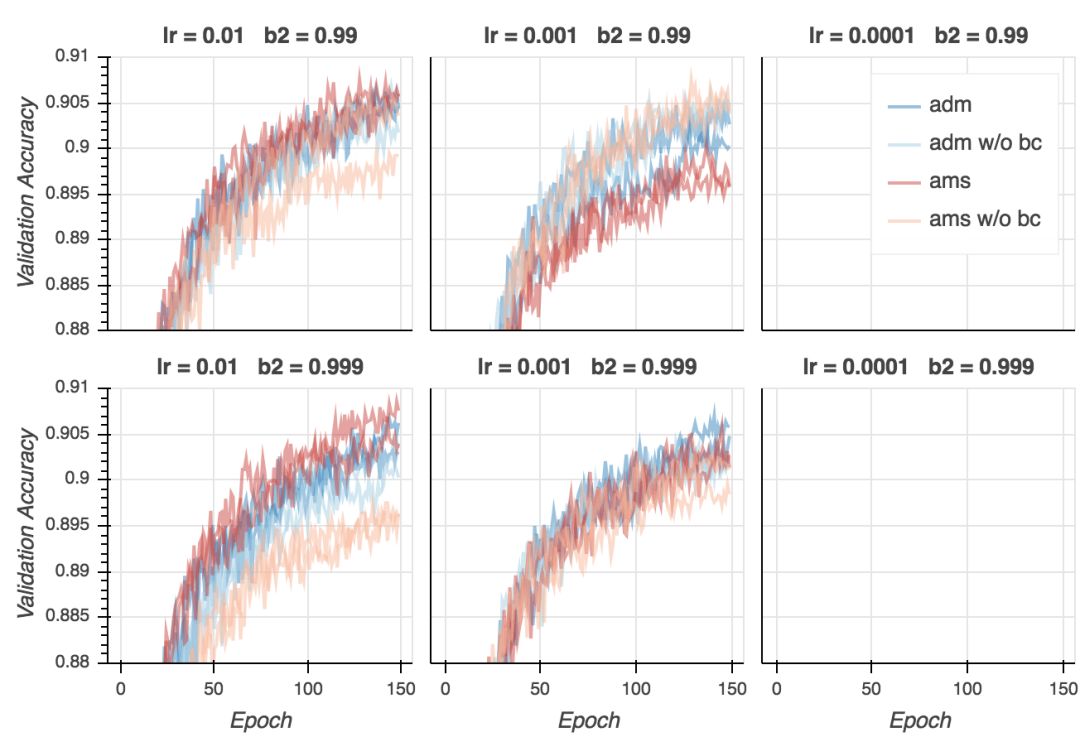
最后，到了最有意思的部分——验证精确度。

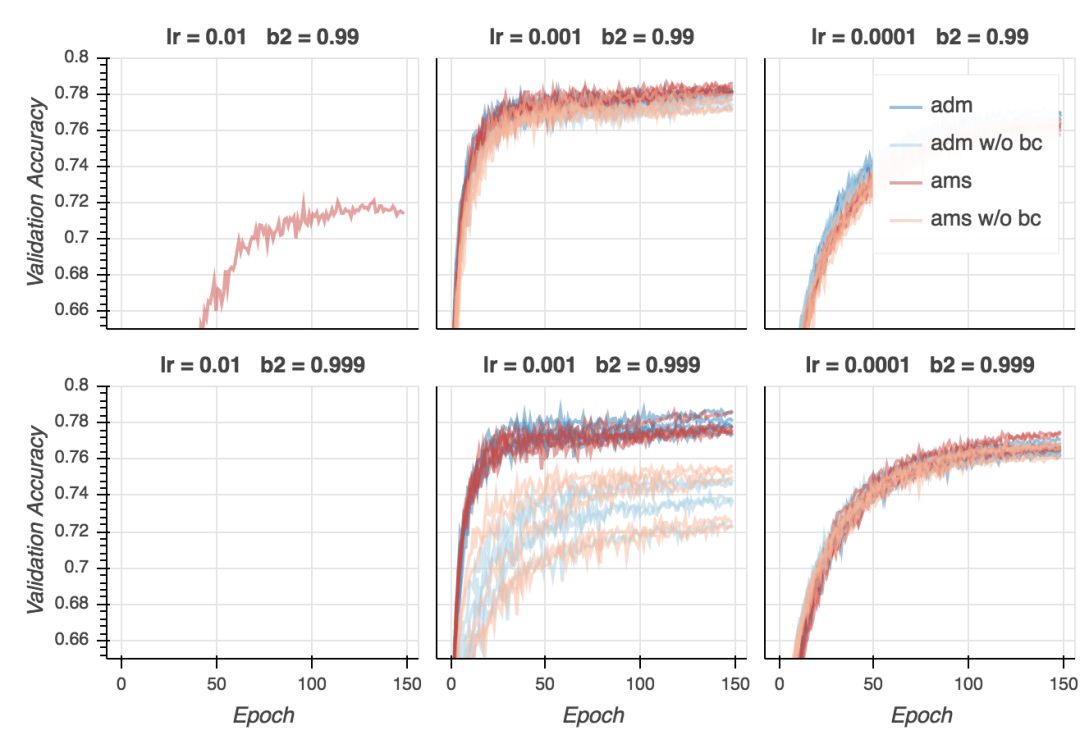
验证精确度

现在是失望时刻。尽管在所有超参数配置上，AMSGrad的验证损失更低，从验证精确性来看，基本是平局。在某些设定下，Adam表现更好（lr = 0.01、b2 = 0.999），在其他一些设定下，AMSGrad（lr = 0.001、b2 = 0.999）表现更好。在所有配置中取得最好结果的是Adam（lr = 0.001、b2 = 0.99），但我认为这一差别并不显著。看起来，给定合适的超参数设定，两个算法的表现差不多好。

讨论

论文指出了Adam收敛性证明的一个致命缺陷，并展示了一个证明成立的Adam变体，AMSGrad。然而，我发现论文对AMSGrad的实际影响的试验评估比较有限。在论文中，作者声称（着重由我所加）“AMSGrad在训练损失和精确度上表现得比Adam好多了。此外，这一表现提升同样转换到了测试损失上。”不幸的是，就我使用的模型和训练方案而言，我的试验不能证实这些：

无论是基于损失，还是基于精确度，两者在训练集上的表现类似。
AMSGrad的测试（这里是验证）损失确实比较低。然而，
测试损失上的提升并没有转换为更好的测试精确度（公平起见，作者从来没有声称这一点）。
测试损失和测试精确度间的表现差异提出了一个关键的问题：类别交叉熵训练用于分类的神经网络有多合适？我们能做得更好吗？

特此声明：我确实非常欣赏论文作者指出Adam弱点的工作。尽管我并没有验证证明（显然，直到这篇论文，都没人验证Adam的证明），我倾向于相信他们的结论。同时，人造样本确实表明Adam在特定条件下无法工作。我认为这是一篇好论文。

然而，实际影响需要更多的以经验为基础的探索。我在本文中描述的试验并没有表明Adam和AMSGrad之间在实践上有很大的差异。

附录

这里我展示其他设定的结果。

MNIST上的逻辑回归

这一设定和论文中的一个试验类似。唯一的差别是学习率：论文使用的是α/√t，其中t为迭代，而我使用的是之前提到的每个epoch后的线性衰减。让我们看下结果。

训练损失

我们首先看到的是，线性学习率衰减可以得到低得多的训练损失。在论文中，训练曲线看起来在5000多次迭代（batch大小128，约13个epoch）后，在约0.25处保持平坦。而在我的试验中，取决于超参数，它达到了0.2. 另外一个有趣的发现是，在所有配置中，Adam取得了最低的最终训练损失。这和论文中的结果相反，特别是论文声称的，相比Adam，AMSGrad对参数变动更加强韧（robust）。

验证损失