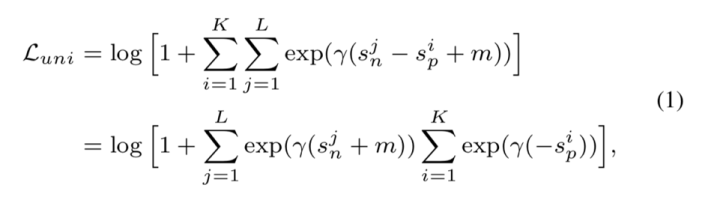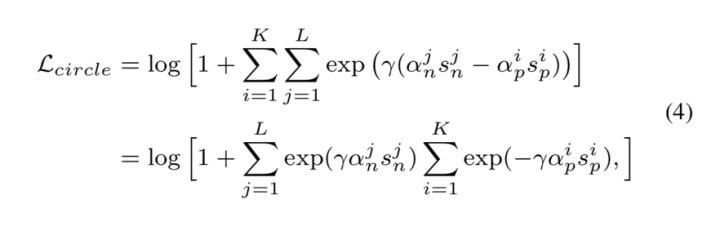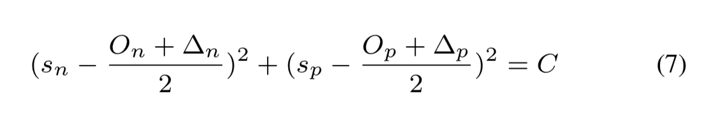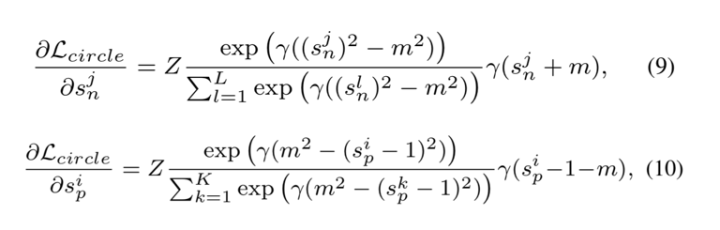入选 CVPR 2020的旷视论文，到底写了啥？

2020 年 3 月 28 日 CSDN

作者 | 旷视研究院

【CSDN编者按】本文是旷视 CVPR 2020的被收录论文解读第。它提出用于深度特征学习的Circle Loss，从相似性对优化角度正式统一了两种基本学习范式（分类学习和样本对学习）下的损失函数。通过进一步泛化，Circle Loss 获得了更灵活的优化途径及更明确的收敛目标，从而提高所学特征的鉴别能力；它使用同一个公式，在两种基本学习范式，三项特征学习任务（人脸识别，行人再识别，细粒度图像检索），十个数据集上取得了极具竞争力的表现。

深度特征学习有两种基本范式，分别是使用类标签和使用正负样本对标签进行学习。使用类标签时，一般需要用分类损失函数（比如 softmax + cross entropy）优化样本和权重向量之间的相似度；使用样本对标签时，通常用度量损失函数（比如 triplet 损失）来优化样本之间的相似度。

这两种学习方法之间并无本质区别，其目标都是最大化类内相似度（）和最小化类间相似度（）。从这个角度看，很多常用的损失函数（如 triplet 损失、softmax 损失及其变体）有着相似的优化模式：

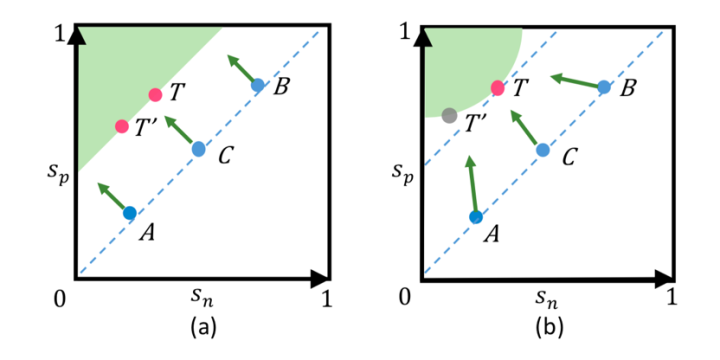
它们会将和组合成相似度对 (similarity pair)来优化，并试图减小（）。在（）中，增大等效于降低。这种对称式的优化方法容易出现以下两个问题，如图 1 (a) 所示。

降低 (

) 的常用优化方法与新提出的降低 (

) 的优化方法之间的对比

优化缺乏灵活性

和上的惩罚力度是严格相等的。换而言之，给定指定的损失函数，在和上的梯度的幅度总是一样的。例如图 1(a)中所示的 A 点，它的已经很小了，可是，会不断受到较大梯度。这样现象低效且不合理。

收敛状态不明确

优化 ( ) 得到的决策边界为（m 是余量）。这个决策边界平行于维持边界上任意两个点（比如和）的对应难度相等，这种决策边界允许模棱两可的收敛状态。比如，和都满足了的目标，可是比较二者时，会发现二者之间的分离量只有 0.1，从而降低了特征空间的可分性。

简介

为此，旷视研究院仅仅做了一项非常简单的改变，把 ( ) 泛化为 ( )，从而允许和能以各自不同的步调学习。

具体来讲，把和分别实现为和各自的线性函数，使学习速度与优化状态相适应。相似度分数偏离最优值越远，加权因子就越大。如此优化得到的决策边界为，能够证明这个分界面是 ( ) 空间中的一段圆弧，因此，这一新提出的损失函数称之为 Circle Loss，即圆损失函数。

由图 1(a) 可知，降低 ( ) 容易导致优化不灵活（A、B、C 相较于和的梯度都相等）以及收敛状态不明确（决策边界上的 T 和 T' 都可接受）；而在 Circle Loss 所对应的图 1 (b) 中，减小 ( ) 会动态调整其在和上的梯度，由此能使优化过程更加灵活。

对于状态 A，它的很小（而已经足够小），因此其重点是增大；对于 B，它的很大（而已经足够大），因此其重点是降低。此外，本文还发现，圆形决策边界上的特定点 T （圆弧与45度斜线的切点）更有利于收敛。因此，Circle Loss 设计了一个更灵活的优化途径，通向一个更明确的优化目标。

Circle Loss 非常简单，而它对深度特征学习的意义却非常本质，表现为以下三个方面：

1、统一的（广义）损失函数。从统一的相似度配对优化角度出发，它为两种基本学习范式（即使用类别标签和使用样本对标签的学习）提出了一种统一的损失函数；

2、灵活的优化方式。在训练期间，向或的梯度反向传播会根据权重或来调整幅度大小。那些优化状态不佳的相似度分数，会被分配更大的权重因子，并因此获得更大的更新梯度。如图 1(b) 所示，在 Circle Loss 中，A、B、C 三个状态对应的优化各有不同。

3、明确的收敛状态。在这个圆形的决策边界上，Circle Loss 更偏爱特定的收敛状态（图 1 (b) 中的 T）。这种明确的优化目标有利于提高特征鉴别力。

统一的相似性优化视角

深度特征学习的优化目标是最大化，最小化。在两种基本学习范式中，采用的损失函数通常大相径庭，比如大家熟知的 sofmax loss 和 triplet loss。

这里不去在意相似性计算的具体方式——无论是样本对之间的相似性（相似性对标签情况下）还是样本与类别代理之间的相似性（类别标签情况下）。本文仅仅做这样一个假设定义：给定特征空间中的单个样本 x，假设与 x 相关的类内相似度分数有 K 个，与 x 相关的类间相似度分数有 L 个，分别记为和。

为了实现最大化与最小化的优化目标，本文提出把所有的和两两配对，并通过在所有的相似性对上穷举、减小二者之差，来获得以下的统一损失函数：

这个公式仅需少量修改就能降级得到常见的 triplet 损失或分类损失，比如得到 AM-Softmax 损失：

或 triplet 损失：

Circle Loss：自定步调的加权方式

暂先忽略等式 (1) 中的余量项 m 并对和进行加权，可得到新提出的 Circle Loss：

再定义的最优值为，s_n 的最优值为；。当一个相似性得分与最优值偏离较远，Circle Loss 将分配较大的权重，从而对它进行强烈的优化更新。为此，本文以自定步调（self-paced）的方式给出了如下定义：

类内余量和类间余量

不同于优化 ( ) 的损失函数，在 Circle Loss 中，和是不对称的，本文为其各自定义了余量和，这样可得到最终带余量的 Circle Loss：通过推导决策边界，本文进一步分析 ∆_n 和 ∆_p。为简单起见，这里以二元分类的情况进行说明，其中决策边界是在处得到。根据等式 (5) 和 (6) ，可得到决策边界：

Circle Loss 有 5 个超参数，即、、、和。通过将，，，。可将等式 (7) 约简为：

基于等式 (8) 定义的决策边界，可对 Circle Loss 进行另外一番解读。其目标是优化和。参数 m 控制着决策边界的半径，并可被视为一个松弛因子。

换句话说，Circle Loss 期望且。因此，超参数仅有 2 个，即扩展因子和松弛因子。

优势

Circle Loss 在和上的梯度分别为：

损失函数的梯度：（a）三重损失；（b）AMSoftmax 损失；（c）新提出的 Circle 损失

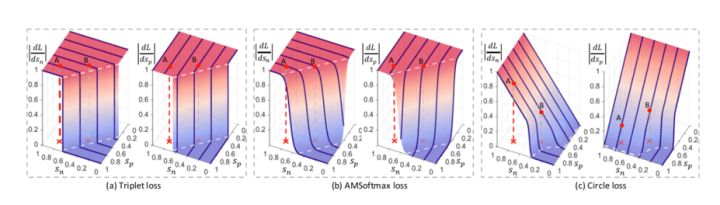
上图的可视化结果表明，triplet 损失和 AMSoftmax 损失都缺乏优化的灵活性。它们相对于（左图）和（右图）的梯度严格相等，而且在收敛方面出现了陡然的下降（相似度配对 B）。比如，在 A 处，类内相似度分数已接近 1 ，但仍出现了较大的梯度。此外，决策边界平行于，这会导致收敛不明确。

相对而言，新提出的 Circle Loss 可根据相似性得分与最优值的距离，动态地为相似度分数分配不同的梯度。对于 A（和都很大），Circle Loss 的重点是优化；对于 B，因为显著下降，Circle Loss 会降低它的梯度，并因此会施加温和的优化。

Circle Loss 的决策边界是圆形的，与直线有着明确的切点，而这个切点将成为明确的收敛目标。这是因为，对于同样的损失值，该切点具有最小的类间-类间差距，是最容易维持的。

实验

本文在三个特征学习任务（人脸识别，行人再识别，细粒度图像检索）上，对 Circle Loss 进行了全面评估，结果如下：

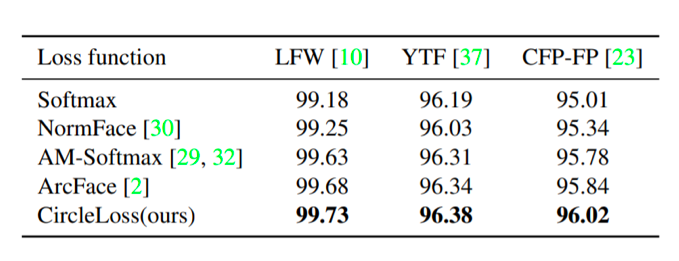
使用不同主干网络和损失函数在 MFC1 数据集上得到的识别 rank-1 准确度（%）

使用 ResNet34 主干网络在 LFW、YTF 和 CFP-FP 上的人脸识别准确度

在 IJB-C 1:1 验证任务上的真实接收率（%）比较

在行人再识别任务上的 Circle 损失的评估，这里报告了 R-1 准确度（%）和 mAP（%）

在 CUB-200-2011、Cars196 和 Stanford Online Products 上与当前最佳结果的比较，这里报告的是 R@K（%）

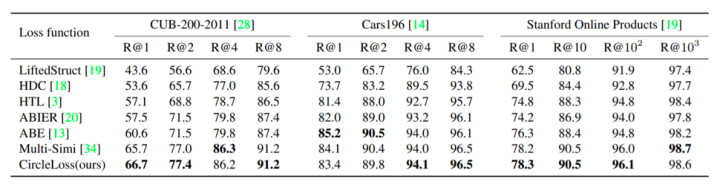
可以看到，在上述三个任务中，Circle Loss 都表现出非常强的竞争力。在人脸上，采用分类模式，Circle Loss 超过了该领域先前的最好方法（如AM-Softmax，ArcFace）；在细粒度检索中，采用样本对学习方式，Circle Loss 又媲美了该领域先前的最高方法（如Multi-Simi）。

值得一提的是，以往这两种范式下的损失函数形式通常大相径庭，而 Circle Loss 则使用完全一样的公式获得了上述表现，且每个参数都具有较好的可解读性。

下面这个关于收敛状态分析的实验，则进一步揭示了Circle Loss的优化特性。