中奖彩票，子网络的觉悟

会员服务 ·

中奖彩票，子网络的觉悟

2020 年 5 月 6 日 机器之心

机器之心分析师网络

作者：张雨嘉

编辑：H4O

本篇对彩票假说的发展及其扩展应用做了分析研究。

如今，深度学习在机器学习中占有非常重要的地位。但随着对深度学习的要求越来越多，需要的网络层数越来越深，参数越来越多，消耗的计算资源也随之扩张，而这很大程度上阻碍了其产业化应用和推广。

从上世纪 90 年代开始，Yan Lecun 等人【1】首先提出了 神经网络剪枝 的思想，即将网络中某些对输出结果贡献不大的参数进行剪除。这种方法可以大大提高模型运行速度，但同时会对模型准确度有一定影响。经过近 30 年的研究，现在的神经网络剪枝技术可以减少训练网络时 90% 以上的参数，以减少存储需求，提高模型的推理计算性能。通常的网络剪枝步骤如下图 1 所示，首先训练一个大的、过参数化的模型，然后根据一定的准则对训练过的模型参数进行修剪，最后将修剪过的模型微调以获得失去的精度。

图 1 经典网络剪枝步骤

然而，既然一个网络可以缩小规模，为什么我们不直接训练这个较小的体系结构，使训练更有效率呢？但是人们通过长期实验发现，网络越稀疏，训练越难、学习速度越慢，所以剪枝产生的稀疏体系结构网络很难从一开始就进行训练。

1. 提出「彩票假说」

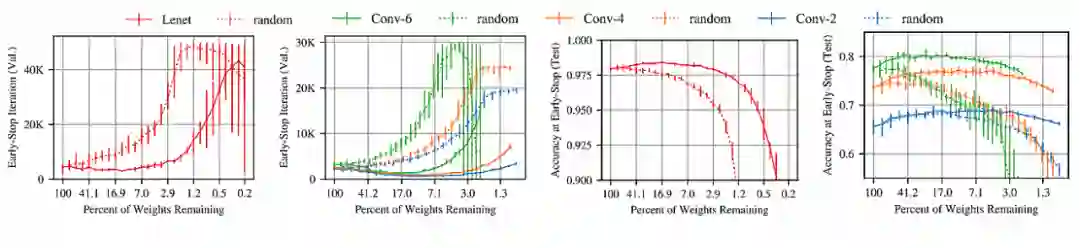
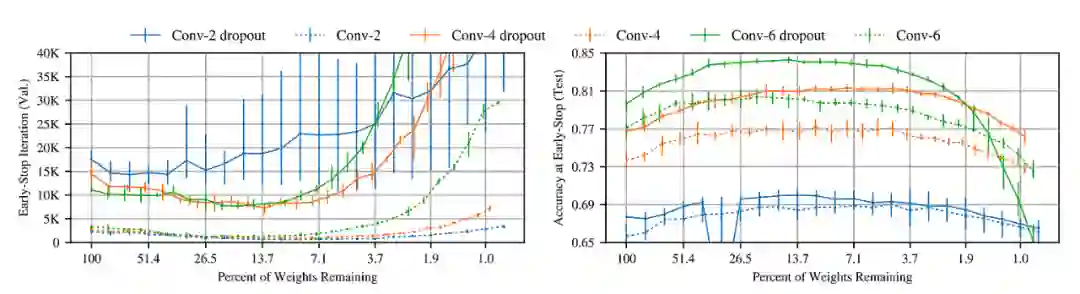
随着网络剪枝研究的深入，Jonathan Frankle 等人【2】发表了一篇名为《The Lottery Ticket Hypothesis :Finding Sparse Trainable Neural Networks》的论文，并获得了 2019 年 ICLR 最佳论文奖。他们发现了一种标准剪枝技术，可以从庞大的原网络中自然地揭示出子网络，并采用合适的初始化使它们能够有效地训练。这种可训练的子网络及其初始化参数被称为「 中奖彩票 」，作者用 Lenet、Conv-2、Conv-4、Conv-6 结构验证了「中奖彩票」（图 2 实线）的优势。横轴代表网络的稀疏性 Pm，例如 Pm=25 时 75% 的权值被修剪。中奖票可以较快进行训练，并达到与原网络相似的精度。

图 2 不同网络剪枝结果

基于此，作者提出了论文的核心思想——「 彩票假说 」。即随机初始化的密集神经网络包含一个初始化的子网络（winning ticket），当它进行隔离训练时可以与原始网络的测试精度相匹配。与理论相对应的剪枝方法可以自动从全连接和卷积前馈网络中找到这种可训练的子网络。其基本步骤为：

随机初始化神经网络 f(x;θ)
训练 j 次迭代网络，得出参数θj
对θj 中参数的 p% 进行修剪，生成掩码。
用θj 中的剩余参数初始化结构，产生中奖票。

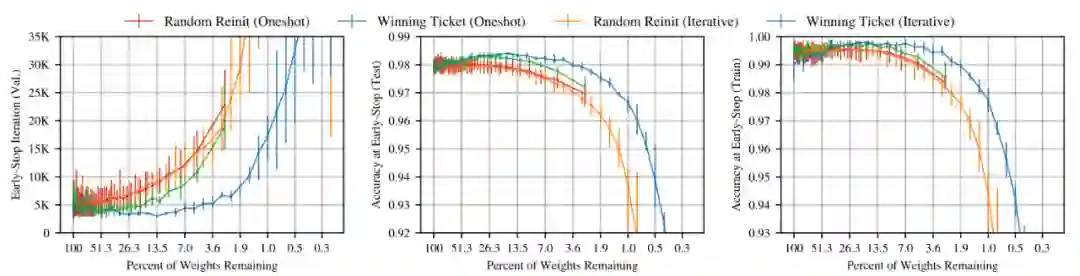
从第三步可以看出，这种剪枝方法是一次性（one-shot）的：训练一次网络，修剪 p% 的权重，重置剩余的权重。然而，作者将重点放在迭代（iteration）剪枝上（如图 3），它反复地训练、修剪并重置网络。实验发现， 当与原始网络的精度相匹配时，迭代剪枝可以提取到较小的获胜票 ，但重复训练也意味着它们的查找成本很高。

图 3 不同初始化和剪枝方法下的网络性能

中奖票的初始化与中奖票结构同样重要，从左图可以看出， 随机初始化的网络（Random Renit）比用原来网络初始化（Winning Ticket）的学习速度慢，在修剪率很小时就失去了测试精度。

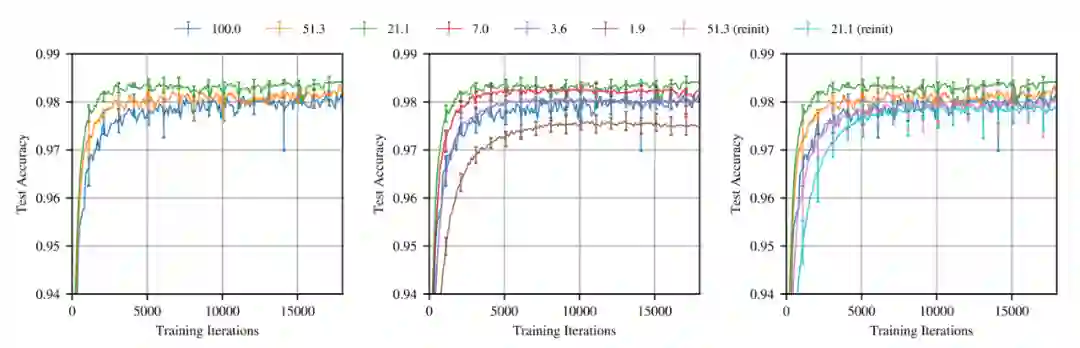
作者在全连接网络 Lenet 上用 MNIST 数据集按迭代剪枝的方法进行训练，结果见图 4，绘制了训练中奖彩票迭代修剪到不同程度时的平均测试精度，label 为不同修剪程度。当 Pm>21.1 时，网络越修剪，学习速度变快（左图）。当 Pm<21.1 学习速度减慢（中图），当 Pm=3.6% 时，中奖彩票会回到原来网络相似的表现。大部分中奖票的准确率明显高于原始网络，这意味着中奖彩票的训练精度和测试精度之间的差距较小，泛化能力有所提高。

图 4 不同修剪率下的 Lenet 测试精度

之后，作者还用 Cifar-10 数据集在卷积网络上进行了相同的实验，得到了与前面相同的结论。随着网络的修剪，中奖彩票与原始网络相比，学习速度更快，测试精度更高，泛化能力更强。同时证明了 Dropout——2012 年 Hinton 等人【3】提出通过随机禁用每次训练中的一小部分（即随机采样一个子网络）来提高测试精度——在中奖票的训练中同样适用。从图 5 中看出， Dropout 可以提高初始测试精度，但学习速度变慢。所以需要以互补的方式同时采用迭代剪枝策略与 Dropout，以更快找到中奖彩票。

图 5 Dropout 对网络剪枝的影响

最后，为了证明在更深层网络中中奖彩票的有效性，作者在 VGG 和 ResNet 网络中找寻中奖票。与前面以相同比例分别修剪每一层的 Lenet 和 Conv-2/4/6 不同，ResNet-18 和 VGG-19 是在所有卷积层中修剪贡献较低的权值（Global Pruning）。因为对于这些更深的网络，有些层的参数远多于其他层。如果所有层都以同样的比例修剪，这些较小的层就会成为瓶颈，阻止我们找出结构最小的中奖票。

图 6 不同学习率下的 VGG-19 剪枝

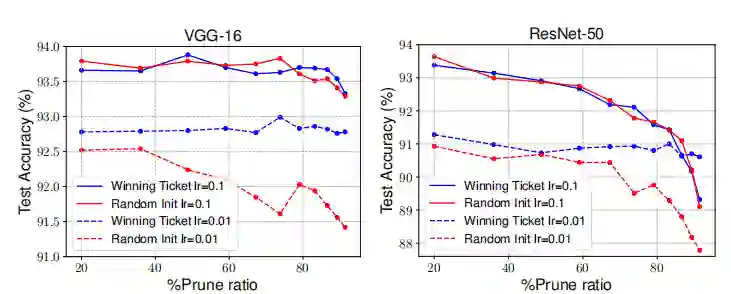
不过从实验结果（图 6）发现，在较高的学习率下，迭代剪枝找不到中奖票，并且性能比剪枝网络随机初始化时更差。但在较低的学习率时，可以得出与之前相同的结论：在 Pm≥3.5 时，子网络比原网络的精度始终高 1%。如果随机重新初始化（rand reinit），子网络又会失去准确性。

为了弥补学习率较高时中奖票低性能问题，作者提出了线性学习速率热身（warmup）方法，即在 k 次迭代中从学习率 0 到初始值。从图中绿线可以看出，warmup 提高了高学习率下的测试精度，使找到中奖彩票成为可能。不过在 ResNet 上的实验结果却说明，通过热身训练的中奖票虽然缩小了与未修剪网络的准确性差距，但仍有可能找不到中奖票。不过这些实验仍能给我们一些启发，比如如何设计更好的网络结构、进一步提高模型性能等。

2. 假说争议探讨

大胆的「彩票假说」理论一经发布，也引发了相关领域学者的注意。在 ICLR 上同年发表的另一篇名为《Rethinking the Value of Network Pruning》【4】的论文中，Liu 等人对「彩票假说」进行了重新实验并提出了异议。

Liu 与 Jonathan Frankle 使用相同的非结构化剪枝方法时，高学习率下的原网络初始化对网络剪枝没有显著影响，只在低学习率下对模型有些许提高（图 7）。但 Facebook 的田渊栋团队在论文《One ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers》【5】中也指出 warmup 对高学习率下的网络剪枝是非常必要的，而 Liu 等人在实验中并没有实现。

图 7 不同学习率和初始化下网络剪枝性能

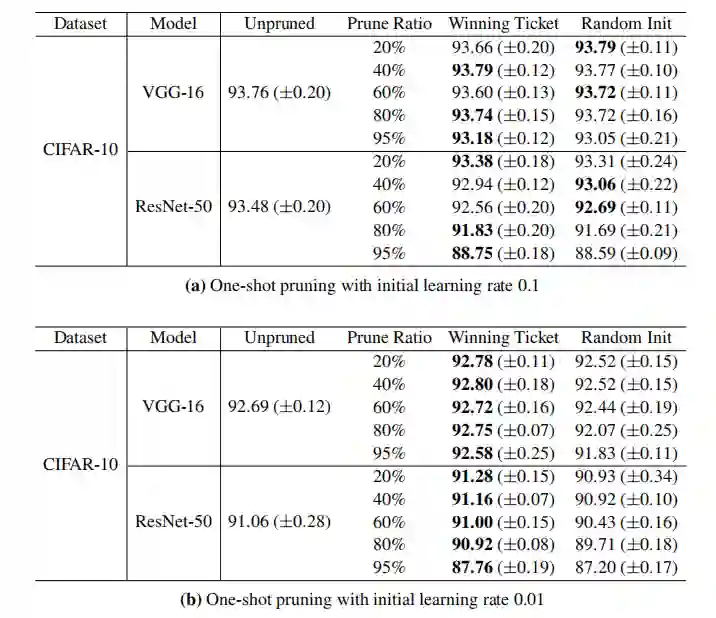
并且对于随机初始化的问题，Liu 也进行了进一步研究（图 8）。 中奖票只在非结构化剪枝下、初始学习率较小时有效，其余时候不如随机初始化的性能好 。而且与大学习率相比，这种小学习率的准确性明显较低。不过这组实验只考虑了 One-shot 方法，至于在迭代剪枝上是否有相同结论还有待探讨。

图 8 一次剪枝下的网络性能

3. 扩充并改进「彩票假说」

论文链接： https://arxiv.org/pdf/1903.01611.pdf

「彩票假说」最被人质疑的地方在于数据集，实验只采用了 MNIST 和 Cifar-10 这种较小的简单数据集，而对更普遍的 Cifar-100 和 ImageNet 数据集并没有进行研究。不过，Jonathan Frankle 和田渊栋等人很快都进行了实验补充。

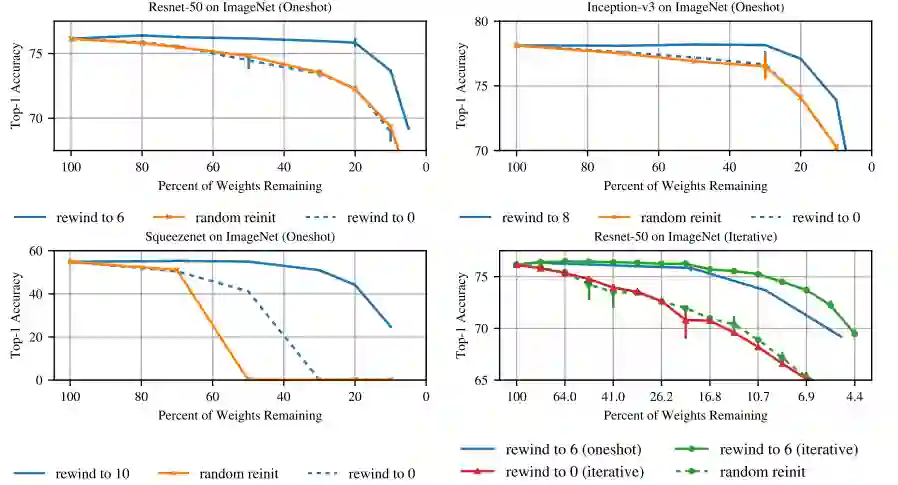
Jonathan Frankle 在《Stabilizing the Lottery Ticket Hypothesis》【6】中对「彩票假说」进行了更深层次的研究。为了证明新的迭代剪枝方法（IMP）在大数据集的有效性，图 9 显示了在 ImageNet 数据集上执行不同代 rewinding 方法的效果。rewinding 是对剪枝网络初始化的一种新方法，将修剪过的子网络权重设为第 k 次迭代时的值，而不是像「彩票假说」中一样将它们 resetting 为第 0 次迭代的值。

图 9 rewind 对中奖彩票的影响

在这些大数据集支撑的更深层次的网络上的实验，IMP 没有任何证据支持 Frankle 和 Carbin 在「彩票假说」里的假设：rewind to 0 比随机初始化（reinit）时能找到能力更好的子网络。但是，rewinding 在训练开始的几代内，可以找到具有这些优良性能的子网络。

从图 9 也能看出，当随机重新初始化（橙色线）或重置为 0 次迭代（虚线蓝线）时，任何程度修剪的子网络都会失去准确性，这说明 rewind 得到的权重是必不可少的。之后作者又引入了子网络稳定性概念：同一子网络受到两个不同噪音影响时产生的差异。提高剪枝的稳定性意味着子网络更接近原始网络的最优情况，从而具有更高的准确性。而稳定性的衡量来源于两方面：pruning，隔离训练的子网络权重与在较大网络内训练的同一子网络权重之间的距离；data order，用不同顺序的数据训练的子网络权重之间的距离。

图 10 网络稳定性比较

图 10 中，在 VGG19 网络上对 rewinding 对剪枝网络稳定性影响的实验中，横轴为 rewinding 重设迭代的次数，procedure 为「彩票假说」中寻找中奖票的迭代剪枝（IMP）方法，random 则为随机剪枝方法。第一行为 data order 距离，第二行为 pruning 距离。而 L2 距离是衡量稳定方法的一种，距离越小，网络越稳定，性能越好。随着 rewinding 次数增加，L2 距离大多减小，IMP 子网络的稳定性与重设为 0 次迭代时的稳定性相比有了很大的提高。从第三行的实验中，也可证明 IMP 发现的中奖票比随机子网络表现出更高的准确性。

总之，IMP 子网络比 one-shot 方法更加稳定，可以达到更高的精度。Rewinding 比初始化为 0 代权值的方法找到的子网络准确率更高。但「彩票假说」的核心思想依旧适用——在网络训练的早期进行剪枝；然而，这样做最有效的时刻应该晚于初始化。

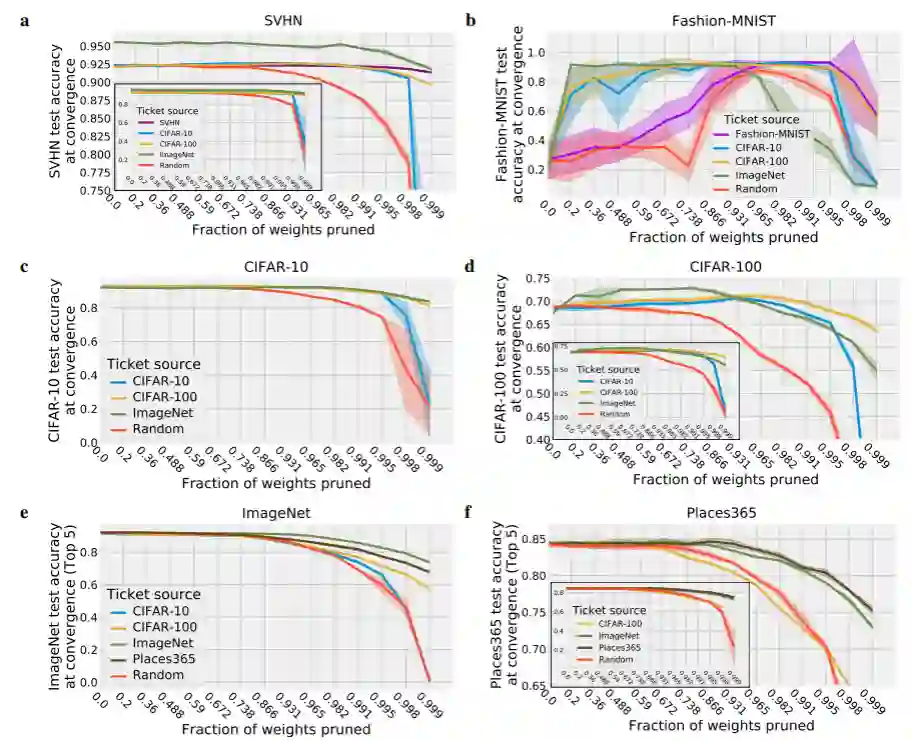
而田渊栋则从另一个方面证明了「彩票假说」在大数据上的有效性。他们用在一个数据集上生成的中奖票推广到同一领域内的不同数据集上，包括 Fashion-MNIST，SVHN，Cifar-10，Cifar-100，ImageNet 和 Places365 数据集。从图 11 的对比试验中发现，在所有数据集上找到的中奖票应用于其他目标数据集上时，其性能与在目标数据集上生成的中奖彩票性能相近。这表明，中奖票所提供的优势中有很大一部分是与数据集无关的（至少在同一领域内）。我们可以生成一次中奖票，但在不同的任务中多次使用，这样可以大大减少寻找中奖票的时间。

图 11 中奖彩票转移实验

而且在更大、更复杂数据集上生成的中奖票性能远远优于小数据集。例如在 ImageNet 和 Places365 数据集上生成的中奖票应用于其他数据集上时，都具有更强的竞争力。当大网络非常过度参数化地处理小数据集时，比如将 VGG19 应用于 Fashion-MNIST 时，发现转移中奖票的性能明显优于在 Fashion-MNIST 本身产生的中奖票，这也为我们提供了另一种处理网络过拟合的方法。

4. 假说的多领域应用

论文链接： https://arxiv.org/pdf/1906.02768.pdf

另有一些学者又提出了质疑：中奖彩票是否为自然图像分类领域出现的特例，还是同样适用于其他领域？Facebook 的田渊栋团队在 2020 年 ICLR 上发布的论文《PLAYING THE LOTTERY WITH REWARDS AND MULTIPLE LANGUAGES: LOTTERY TICKETS IN RL AND NLP》【7】可能能解答这一疑惑。

他们发现「彩票假说」并不局限于对自然图像的监督学习，而是代表了 DNN 中一个更广泛的现象，存在于自然语言处理 (NLP) 和强化学习 (RL) 领域。对于 NLP，我们研究了经典的长短期记忆网络（LSTM）模型和用于机器翻译的 Transformer 模型；在 RL 领域则分析了一个经典控制问题和 Atari 游戏。

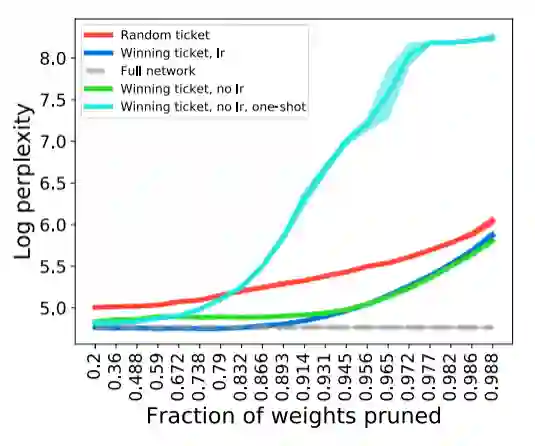
首先，在 Wikitext-2 数据集上对 LSTM 模型的实验中发现，在所有修剪程度上，有 last rewind（即 lr）的中奖票性能明显优于随机票（图 12）。有趣的是，去除 lr（绿色线）对模型性能只有轻微的损坏。这表明对于 LSTM 语言模型来说，lr 方法不太重要。但是迭代修剪是必不可少的，比如使用一次修剪方法（one-shot）时，一旦 80% 的参数被修剪模型性能会急剧下降。这些结果共同验证了中奖彩票在 LSTM 语言模型的有效性。

图 12 LSTM 模型实验

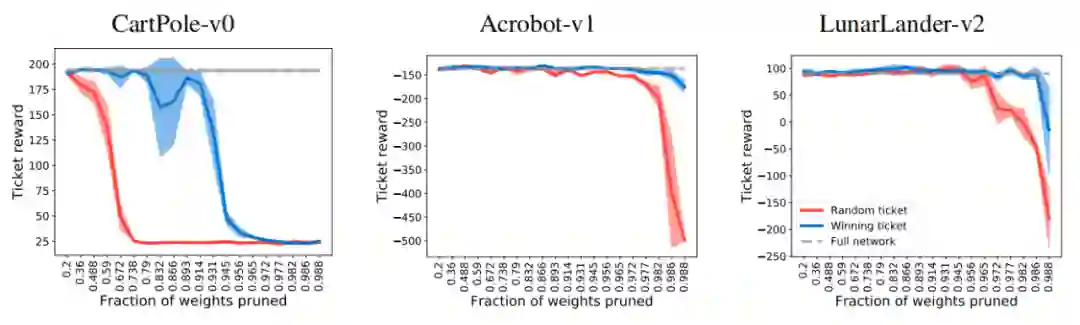
另外在强化学习的应用中，作者在经典控制中选择了三个游戏：Cartpole-v0、Acrobot-v1 和 Lunar Lander-v2，并使用了一个简单三隐层的全连接模型。结论则与图像分类的结果一致（图 13），几乎在所有剪枝程度上，中奖票的得分都超过随机初始化的网络。

图 13 RL 控制模型实验

因此，田渊栋团队认为，彩票假说现象并不局限于有监督的图像分类，而是代表了深层神经网络训练的一般特征。但 Frankle 等人也提出，「彩票假说」的 IMP 方法没有提出一种有效方法来在 rewinding 中找到那些性能优异子网络（即中奖票）。而且采用的核心剪枝技术是非结构化的，与结构化剪枝没有进行有效对比。

不过，大胆的「彩票假说」确实为网络的早期剪枝提供了新视角和方法。暗示了未来技术以识别小的、可训练的子网络，并能够匹配通常训练的较大网络的准确性为目标。通过网络稳定性的研究，对人们开发新的技术来保持网络剪枝时的稳定性有所益处。未来，也希望该理论可以在更深层次的网络中有所表现，在更多的领域有所贡献。

参考文献

【1】Yann LeCun, John S Denker, and Sara A Solla. Optimal brain damage. In Advances in neural information processing systems, pp. 598–605, 1990.
【2】Jonathan Frankle and Michael Carbin. The lottery ticket hypothesis: Finding sparse, trainable neural networks. In International Conference on Learning Representations, 2019.
【3】Geoffrey E Hinton, Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, and Ruslan R Salakhutdinov. Improving neural networks by preventing co-adaptation of feature detectors. arXiv preprint arXiv:1207.0580, 2012.
【4】Zhuang Liu, Mingjie Sun, Tinghui Zhou, Gao Huang, and Trevor Darrell. Rethinking the value of network pruning. In International Conference on Learning Representations, 2019.
【5】Morcos, Ari, et al. One ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers. Advances in Neural Information Processing Systems. 2019.
【6】Frankle, Jonathan, et al. "Stabilizing the Lottery Ticket Hypothesis." arXiv, page.2019.
【7】Yu, Haonan, et al. Playing the lottery with rewards and multiple languages: lottery tickets in RL and NLP. arXiv preprint arXiv:1906.02768, 2019

分析师简介：张雨嘉，现在西安理工大学攻读模式识别方面的硕士学位，主要研究基于深度学习的图像视频处理方法，对机器学习也抱有极大的兴趣。作为机器之心技术分析师的一员，希望能跟各位一起研究探讨，共同提高学习。

关于机器之心全球分析师网络 Synced Global Analyst Network

机器之心全球分析师网络是由机器之心发起的全球性人工智能专业知识共享网络。在过去的四年里，已有数百名来自全球各地的 AI 领域专业学生学者、工程专家、业务专家，利用自己的学业工作之余的闲暇时间，通过线上分享、专栏解读、知识库构建、报告发布、评测及项目咨询等形式与全球 AI 社区共享自己的研究思路、工程经验及行业洞察等专业知识，并从中获得了自身的能力成长、经验积累及职业发展。

感兴趣加入机器之心全球分析师网络？点击 阅读原文 ，提交申请。

登录查看更多