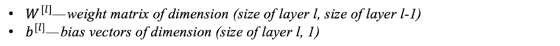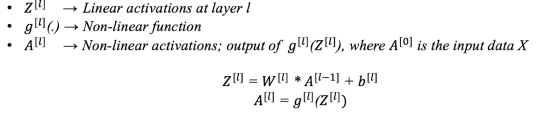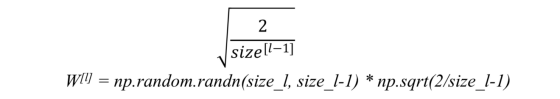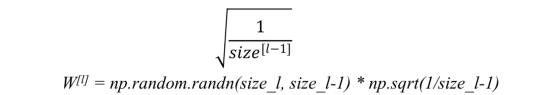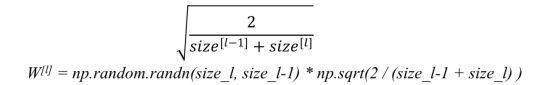【干货】深度学习最佳实践之权重初始化

【导读】深度学习中有很多简单的技巧能够使我们在训练模型的时候获得最佳实践，比如权重初始化、正则化、学习率等。对于深度学习初学者来说，这些技巧往往是非常有用的。本文主要介绍深度学习中权重和偏差初始化以及如何选择激活函数的一些技巧，以及它们对于解决梯度消失和梯度爆炸的影响。

作者 | Neerja Doshi

编译 | 专知

参与 | Yingying, huaiwen

深度学习最佳实践之权重初始化

基础和符号

考虑一个L层神经网络，它具有L-1个隐藏层和1个输出层。层L的参数（权重和偏置表示为

除了权重和偏置之外，在训练过程中，还会计算以下中间变量

训练一个神经网络由4个步骤组成：

1.初始化权重和偏差。

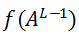
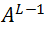
2.正向传播：有输入X，权重W和偏置b，我们们计算每一层Z和A。在最后一层，我们计算，它可能是的S形，softmax或线性函数，它给出了预测y_hat。

3.计算损失函数：这是实际标签y和预测标签y_hat的函数。它表明我们的预测离实际目标有多远。我们的目标是尽量减少这种损失函数。

4.反向传播：在这一步中，我们计算损失函数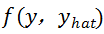相对于A，W和b的梯度，称为dA，dW和db。使用这些梯度，我们将参数的值从最后一层更新到第一层。

5.重复步骤2-4 步n次，直到我们觉得我们已经将损失函数最小化了，同时没有过度拟合训练数据。

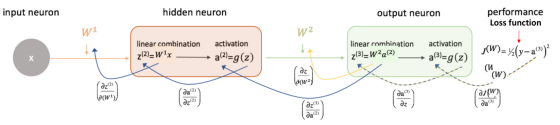
下面是两层网络的第2，3，4步，即一个隐藏层。 （请注意，为了简单起见，我没有在这里添加偏置）：

 初始化权重

建立网络时需要注意的一个起点是正确初始化权重矩阵。在我们考虑在训练模型时可能导致问题的有两种情况：

1. 将所有权重初始化为0 这使得你的模型等价于线性模型。将所有权重设为0时，对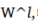中的每个w而言，关于损失函数的导数是相同的，因此所有权重在后续迭代中具有相同的值。这会使隐藏单元对称，并继续运行所有n次迭代。因此，将权重设置为零会使网络并不比线性模型更好。值得注意的是，将偏差设置为0不会产生任何麻烦，因为非零权重可以打破对称性，即使偏差为0，每个神经元仍然不同。

2.随机初始化权重 在使用（深层）网络时，按照标准正态分布（Python中的np.random.randn（size_l，size_l-1））随机初始化权重可能会导致2个问题: 梯度消失或梯度爆炸。

a）梯度消失 - 对于深度网络，对于任何激活函数，abs（dW）将随着反向传播期间而变得越来越小。在这种情况下，前面的层训练较慢。

权重更新较小，导致收敛速度变慢。这使损失函数的优化变得缓慢。在最坏的情况下，这可能会完全阻止神经网络的进一步训练。

更具体地说，在sigmoid（z）和tanh（z）的情况下，如果您的权重很大，那么梯度将会很小，从而有效地防止权重改变它们的值。这是因为abs（dW）会稍微增加，或者每次迭代可能会变得越来越小。使用RELU（z）通常不会出现梯度消失，因为负（和零）输入的梯度为0，正输入为1。

b）梯度爆炸 - 这与梯度消失完全相反。考虑你有非负的，大权重和小的激活函数A（可能是sigmoid（z）的情况）。当这些权重沿层次相乘时，会导致成本发生较大变化。因此，梯度也会很大。这意味着W的变化将增加W-⍺* dW，这个变化是很巨大的。

这可能导致模型在最小值附近振荡，甚至一次又一次超过最佳值，模型将永远不会学习到好的结果！

爆炸梯度的另一个影响是巨大的梯度值可能会导致数字溢出，从而导致不正确的计算或引入NaN。这也可能导致损失值为NaN。

 最佳实践

1.使用RELU / leaky RELU作为激活函数，因为它对梯度消失/爆炸问题（特别是对于不太深的网络而言）相对鲁棒。在 leaky RELU的情况下，它们从不具有0梯度，因此训练会一直进行下去。

2.对于深度网络，我们可以使用启发式来根据非线性激活函数初始化权重。在这里，我们使W服从方差为k/n的正态分布，而不是标准正态分布，其中k取决于激活函数。尽管这些启发式方法不能完全解决梯度爆炸/消失问题，但它们在很大程度上有助于缓解这一问题。最常见的是：

a）对于RELU（z） - 我们将随机生成的W值乘以：

b）对于tanh（z） - 启发式使用Xavier初始化。 它与前一个类似，但k是1而不是2。

在TensorFlow中W = tf.get_variable（'W'，[dims]，initializer）其中initializer = tf.contrib.layers.xavier_initializer（）

c）另一种常用启发式是：

这作为好的初始化值，并缓解爆炸或消失梯度的可能性。他们设置的权重既不会太大，也不会太小。因此，梯度不会消失或爆炸太快。它们有助于避免收敛缓慢，同时确保我们不会一直摆脱最小值。存在上述的其他变体，其中主要目标再次是使参数的方差最小化。

3.梯度截断：这是处理梯度爆炸问题的另一种方法。我们设置一个阈值，如果一个梯度的选择函数大于这个阈值，我们将它设置为另一个值。例如，当L2范数超过特定阈值时归一化梯度：W = W * threshold / l2norm（W）如果l2norm（W）>阈值

需要注意的是，我们已经谈到了W的各种初始化方法，但没有设计偏置b。这是因为偏置的梯度仅取决于该层的线性激活，而不取决于较深层的梯度。因此，对于偏差项不存在递减或爆炸的梯度。如前所述，它们可以初始化为0。

 结论

在这篇博客中，我们介绍了权重初始化陷阱和一些缓解技术。

参考文献：

https://towardsdatascience.com/deep-learning-best-practices-1-weight-initialization-14e5c0295b94

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！加入专知主题群（请备注主题类型：AI、NLP、CV、 KG等）交流~

投稿&广告&商务合作：fangquanyi@gmail.com

点击“阅读原文”，使用专知