Efficient Diverse Ensemble for Discriminative Co-Tracking

CVPR2018的一篇论文

论文链接：https://arxiv.org/abs/1711.06564

一、背景

将集成学习用于目标跟踪可以提高跟踪结果的可靠性。但是现有的相关方法仍然存在多个问题：(1) 更新集成中的分类器时使用的样本集过于重复，导致集成的多个分类器之间存在不必要的冗余。(2) 更新分类器时，使用的样本的标签都是首先由分类器本身给出的，并不能确保这些标签都是正确的，随着时间的推移，会造成累计误差。

针对这几个问题，本文做了一些改进，具体的改进和贡献如下：

(1) 使用主动学习中的QBC算法(Query by Committees)，除了集成的分类器之外，引入了一个辅助的分类器，对于集成分类器不是很确定的样本，借助辅助分类器来进行分类。

(2) 只有当多个分类器之间更具差异性和多样性的时候，集成学习才能发挥更大的威力。所以除了采集到的样本外，文中还使用了人造样本来更新集成中的每个分类器，由于人造样本之间不存在重复现象，因此可以使得所有分类器更加多样化。

(3) 集成分类器每帧都进行更新，且只使用难分类样本和人造样本进行更新，因此可以很好的捕捉到目标的突然性的表观变化；而辅助分类器则只进行定期的更新，因此更具有长时记忆功能。这样使得跟踪算法既有短时记忆，又具备长时记忆。

二、算法细节

算法流程：

1、首先在第一帧目标位置附近选取样本，训练辅助分类器以及集成分类器C_t中的C个分类器。

2、对于待跟踪的第t帧图像(t=2,3,……,T):

       (1)以上一帧的目标位置为中心，根据高斯分布随机取n个样本。

(2) 将这n个样本依次放入集成分类器中进行分类，对于每个样本，若结果大于T_u，则将其分为正类；若小于Tl，则将其分为负类；若在Tl和T_u之间，则将其放入辅助分类器中进行分类，辅助分类器的结果即为这个样本最终的分类结果(QBC算法)。

(3) 将所有的n个样本都放入样本集D_t中，且将(2)中集成分类器难以分类的样本放入到难分类样本集U_t中。

(4) 对于集成中的C个分类器，依次更新每个分类器，得到新的暂时的集成分类器C'_t，更新方法为：从难分类样本集U_t中随机选取m个样本来训练并更新分类器。(对于不在U中的样本，由于这些分类器原本对它们的分类效果就比较好，因此不予考虑；只使用难分类样本集U_t来更新这些分类器，可以提高集成分类器对于这些样本的分类效果。)

(5) 计算原集成分类器C_t的误差：error(C_t) = |U_t| / |U_t|

(6) 计算样本集D_t的经验分布

(7) 对在(4)中更新得到的暂时的集成分类器C'_t，利用人造样本对其进行再次更新，更新过程如下：对于C'_t中的每个分类器：

       (i) 从样本集D_t的经验分布中随机抽取m'个样本

       (ii) 对于m'个样本，依次将其输入到集成分类器C'_t中，得到它的类概率

(iii) 对于每个样本，以相反的概率设置它的标签。即，如果在(ii)中得到这个样本为正类的概率为p，则以1-p的概率将它的标签设置为正类。

(iv) 根据m'个样本和它们的标签来更新当前分类器，并将得到的集成分类器记为C''_t

(v) 将(1)中取的n个样本放入集成分类器C''_t中，计算分类误差error(C''_t)

(vi) 比较error(C''_t)和error(C_t)，如果前者大于后者，说明使用人造样本更新后的集成分类器反而变差了，此时不会保留C''_t，并重复(i)-(v)。直到error(C''_t)小于error(C_t)为止，然后才将C''_tt保留

(8) 经过(4)-(7)，集成分类器分别利用难分类样本集和人造样本集进行了更新，记为C_t+1

(9) 如果mod(t,a)=0，则更新辅助分类器，即每隔a帧更新辅助分类器。更新时使用的样本集为最近a帧所取的所有样本

对于算法流程的几点说明：

对(2)的解释：

假设集成中包含C个分类器，正样本标签为1，负样本标签为-1。对于每个待分类样本，将其输入集成分类器中可以得到C个结果，采用无权重投票的方式得到最终的分类结果，即将这C个结果简单的相加在一起。所有分类器结果相加得到的数为正数则说明集成分类器将其分为正类，为负数将其分为负类，且绝对值越大说明集成中分类器的分类结果越一致，结果也就越可靠。反之，如果最终得到的数在0附近，则说明集成中的分类器对这个样本分歧越大。文中设置了两个阈值Tu和Tl，其中Tu为正数，Tl为负数，若最终的结果大于Tu，则样本被分为正类；若结果小于Tl，则样本被分为负类；在Tl和Tu之间则说明集成中的分类器对样本分歧太大，无法得到比较可靠的结果，此时需要借助辅助分类器来对其进行分类，并且该样本可以理解为难分类样本，需要放入难分类样本集Ut。

对(7)的解释：为什么使用难分类样本集对集成分类器更新后，还要使用人造样本对其更新？

集成分类器只有在组成集成的多个分类器存在明显的差异性和多样性时，才能发挥出更好的效果。使用人造样本可以极大的降低训练这些分类器所使用的样本集之间的重复率，使得训练得到的多个分类器之间存在一定的差异性和多样性。

对(7)中(iii)的解释：为何要以相反的概率来设置人造样本的标签？

这里其实也用到了选取难分类样本来更新分类器的思想。试想一下，对于一个人造样本，如果集成分类器判断它属于正样本的概率为0.9，那么在(iii)中，将以0.1的概率将它的标签置为1，而0.9的概率置为-1。集成分类器原本很确定它就是正类，但是经过(iii)以后反而将它的标签置为负类了，然后再用这个错误的标签来训练更新集成分类器，得到的分类器必然变差了，分类误差error(C''_t)很有可能会大于error(Ct)，所以需要重新选取人造样本然后重新更新分类器。所以说，这一步操作的目的在于，如果人造的样本放入集成分类器很容易、很明确就可以被分类的话，这些样本就会被丢弃不用，直到人造样本是一些难分类样本时才会被用来进行更新集成分类器。这和(4)中只使用难分类样本集更新集成分类器的思想相同。

三、实验

1、集成分类器的多样性的效果

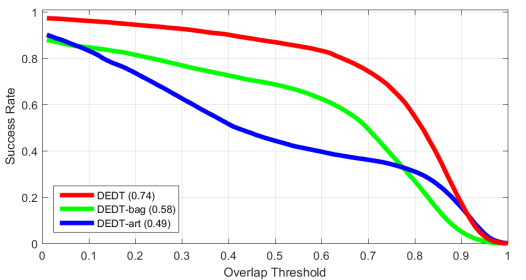
为了验证集成分类器多样性和差异性对跟踪结果的影响，文中使用了三种不同的跟踪器来对比它们的结果，分别是：DEDT(即文中提出的方法)、DEDT-bag(只使用难分类样本集Ut来更新集成分类器)、DEDT-art(只使用人造样本来更新集成分类器，不使用Ut)。对比结果如下：

可以看到，DEDT > DEDT-bag > DEDT-art，可以看出，由于DEDT相比DEDT-bag，除了难分类样本集Ut之外，还使用了可以使集成分类器更具多样性和差异性的人造数据，所以效果更好。而DEDT-art虽然由于人造样本的存在，多样性和差异性好于DEDT-bag，但是由于全部使用的是人造样本，缺乏真实采样得到的更可靠的样本，所以效果不如DEDT-bag。

2、使用人造数据的效果

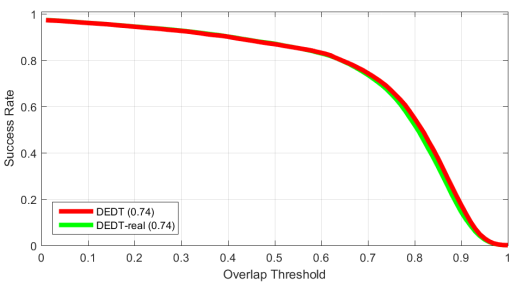
对了验证人造数据的合理性，文中对图像通过滑动窗口进行了密集采样，然后对于每个人造样本，根据欧氏距离计算出它与密集采样得到的样本集中最相似的真实样本，用对应的真实样本代替人造样本来进行更新集成分类器。实验结果对比如下：

其中DEDT表示文中的方法，DEDT-real表示真实样本代替人造样本的方法。可以看出，两者的效果几乎没有任何差别。而与滑动窗口密集采样相比，使用人造样本可以极大的降低计算复杂度。

3、主动学习中“主动性”的影响

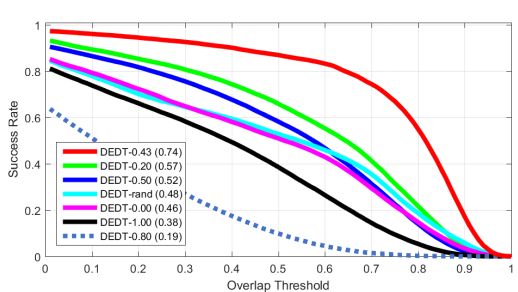
阈值Tu和Tl控制了主动学习的QBC算法中的主动性。它们的绝对值越大，说明辅助分类器使用的会更频繁。Tu和Tl是两个独立的值，为了简单起见，实验中只取它们的绝对值相同的情况。实验结果如下：

其中DEDT-rand指的是对于每个样本，随机使用辅助分类器和集成分类器中的一个对其进行分类，且随机选取两者的概率相同。当Tu和Tl都为0的时候，即只使用集成分类器而不使用辅助分类器；而当它们的绝对值都为1，即Tu=1，Tl=-1的时候，相当于只使用了辅助分类器，而不使用集成分类器，此时跟踪器退化为单分类器的情况。可以看到，选取合适的阈值，对于跟踪的性能至关重要。

4、和state-of-the-art方法的比较

和现有的顶尖方法的比较结果如下：