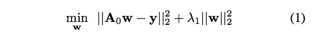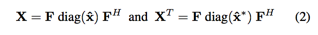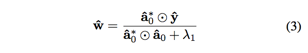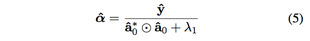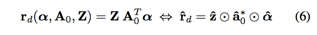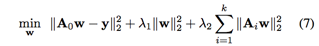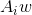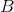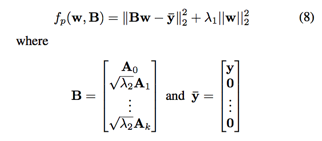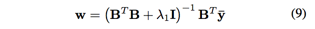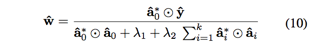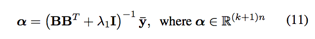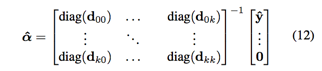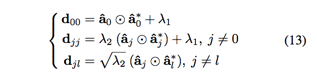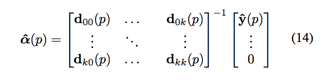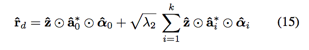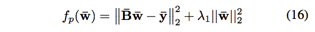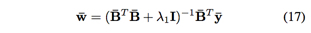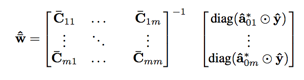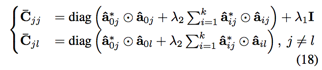上下文感知相关滤波跟踪

Context-Aware Correlation Filter Tracking 论文笔记

CF+CA: Matthias Mueller, Neil Smith, Bernard Ghanem. “Context-Aware Correlation Filter Tracking.” CVPR (2017).

原文链接

项目地址

源码

动机

基于相关滤波的跟踪方法目前获得了极大的成功，也有了大量改进工作，但是仍然存在一些问题：

• 目前的工作主要集中在利用强大的特征获取被跟踪目标更好的表示

• 目前的相关滤波方法只能在一个很小的区域内区分出目标和背景，所以对于目标的快速运动判别能力不强

• 在跟踪过程中目标周围的背景信息对性能有极大的影响，尤其在背景复杂时表现尤其

主要贡献

• 提出了一种将背景信息融入相关滤波方法中的跟踪框架

• 推导了上下文感知相关滤波的解析解，并从单通道推广到了多通道，从原始域推广到了对偶域

• 大量的实验证明，论文提出的框架能够应用在很多相关滤波方法中，在不影响速度的同时显著提升性能

基本思路

框架概况

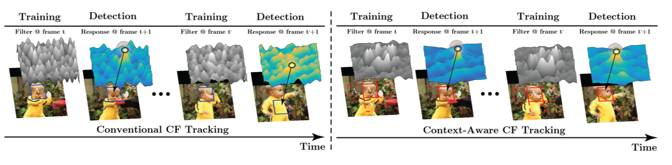
方法的整体思路如下图所示，

左图是原始相关滤波方法的跟踪过程，由于相关滤波的边际效应，在检测过程中得到的响应图往往存在多个峰值，如果目标外观变化显著，此时目标真实位置的峰值并不是最大，从而造成误判，造成跟踪失败

右图是上下文感知相关滤波方法的跟踪过程，由于在训练过程中加入背景信息，使得训练得到的滤波器更具判别性，在检测过程中次峰值会被抑制

相关滤波原始问题

目标函数如下

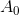
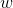
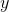
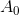
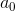
通过循环样本矩阵训练得到滤波器，训练过程中的标签是一个二维高斯形状，循环样本矩阵是原始样本通过循环移位得到

利用循环矩阵的性质

以上岭回归问题可以获得在傅立叶域的解析解

检测过程也可以在傅立叶域快速求解

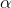
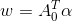
通过引入对偶变量，其中，以上问题还可以转换到对偶域中求解

对偶域中的检测过程与原始域类似

上下文感知相关滤波

鉴于跟踪过程的背景信息往往对判别目标十分重要，本文的重点是将上下文信息融合到相关滤波方法的流程中

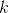
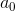
首先在目标区域周围采样个上下文图像块，图像块的大小和候选图像块的大小相同，那么，这些上下文图像块同样可以通过循环移位得到循环样本矩阵

理想的情况是训练得到的滤波器在候选区域得到的响应尽可能的大同时在上下文区域的响应尽可能小，所以推出以下修改后的目标函数

在相关滤波原始问题目标函数的基础上联合最小化上下文区域的响应

上下文区域的损失也可以采用其他形式，如hinge loss，但是，为了保证目标函数的解析解以便于优化，本文直接将上下文区域的标签强制置为0

单通道特征求解

首先将目标函数重写，引入中间变量

由于以上优化问题是凸的，可以视为岭回归，可以得到解析解

转换到傅立叶域后

训练得到滤波器后，检测目标的过程与原始相关滤波方法相同

同样的，问题也可以转化到对偶域求解

此时其傅立叶变化表示为

其中向量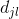由下式得到

由于矩阵中每一块均是对角矩阵，所以可以转换为每一行作为子问题分别求解

在检测阶段，对偶域的形式变为

多通道特征求解

多通道特征的求解通过将特征的每一个通道连接起来实现，即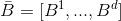，其中

此时，求解得到的滤波器也是多通道的叠堆

利用循环矩阵的性质

其中

对偶域的求解和单通道类似

上下文区域的选择策略

在上下文区域的选取上可以采取多种策略，最简单的方法就是在候选图像块周围选取不重叠的同样大小的图像块，此外，卡尔曼滤波也可以作为一种采样策略，本文实现中采用最简单的区域选取方式

实验结果

实验中本文提出的框架与四种相关滤波方法进行结合，充分表现出框架强大的泛用能力，实验中上下文区域的块数设置为4，即上下左右四块

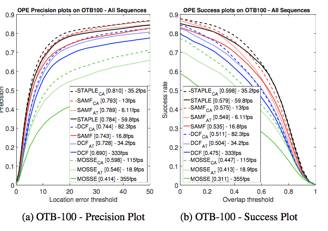
整体性能

分别与MOSSE，DCF，SAMF和STAPLE进行了结合，性能的提升如上图所示，并且与自适应响应相关滤波方法(CF+AT)进行了对比，可以看出本文提出的方法(CF+CA)比CF+AT对于原始方法的提升更大，并且对于速度的影响更小

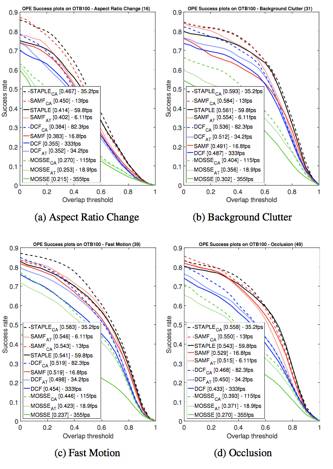
具体性能指标

可以看出，对于目标的尺寸比例变化(Aspect Ratio Change)，背景杂波(Background Clutter)，快速运动(Fast Motion)和遮挡(Occlusion)，CF+CA都表现出强大的性能，尤其在快速运动上提升较大

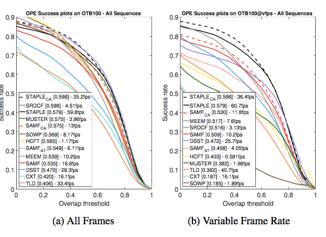
与state-of-the-art方法对比

本文提出的框架与STAPLE的结合获得的性能超过目前最先进的一些跟踪算法

定性实验结果

从以上结果图可以看出，对于目标的快速运动尤其是背景复杂的情况下，本文提出的方法能够有效处理，判别出背景和目标，表现出强大的性能