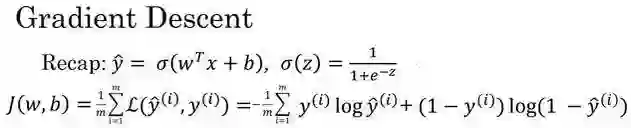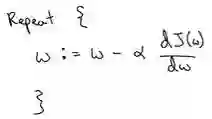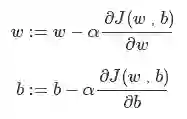课程 | Andrew Ng 深度学习课程笔记5

第二周：神经网络的编程基础 (Basics of Neural Network programming)

2.4 梯度下降（Gradient Descent）

梯度下降法可以做什么 ？

在你测试集上，通过最小化代价函数（成本函数）J(w,b)来训练的参数 w 和 b

如图，在第二行给出和之前一样的逻辑回归算法的代价函数（成本函数）

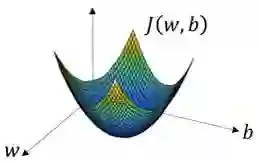
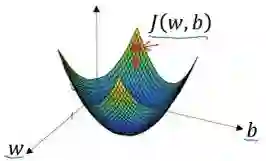
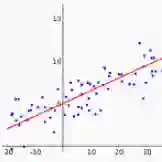
在这个图中，横轴表示你的空间参数 w 和 b，在实践中，w 可以是更高的维度，但是为了更好地绘图，我们定义 w 和 b 都是单一实数，代价函数（成本函数）J(w,b)是在水平轴 w和 b 上的曲面，因此曲面的高度就是 J(w,b)在某一点的函数值。我们所做的就是找到使得代价函数（成本函数）J(w,b)函数值是最小值，对应的参数 w 和 b。

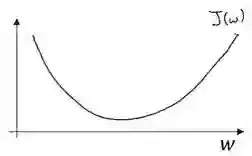
如图，代价函数（成本函数）J(w,b)是一个凸函数(convex function)，像一个大碗一样。

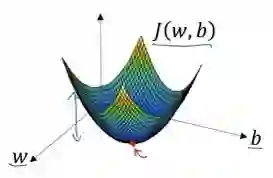
如图，这就与刚才的图有些相反，因为它是非凸的并且有很多不同的局部最小值。由于逻辑回归的代价函数（成本函数）J(w,b)特性，我们必须定义代价函数（成本函数）J(w,b)为凸函数。

1. 初始化 w 和 和 b

可以用如图那个小红点来初始化参数 w 和 b，也可以采用随机初始化的方法，对于逻辑回归几乎所有的初始化方法都有效，因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点。

我们以如图的小红点的坐标来初始化参数 w 和 b。

2. 朝最陡的下坡方向走一步，不断地迭代

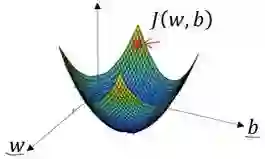
我们朝最陡的下坡方向走一步，如图，走到了如图中第二个小红点处。

我们可能停在这里也有可能继续朝最陡的下坡方向再走一步，如图，经过两次迭代走到第三个小红点处。

3. 直到走到全局最优解或者接近全局最优解的地方

通过以上的三个步骤我们可以找到全局最优解，也就是代价函数（成本函数）J(w,b)这个凸函数的最小值点。

梯度下降法的细节化说明（仅有一个参数）

假定代价函数（成本函数）J(w)只有一个参数 w，即用一维曲线代替多维曲线，这样可以更好画出图像。

迭代就是不断重复做如图的公式： :=表示更新参数，α表示学习率（learning rate），用来控制步长（step），即向下走一步的长度，dJ(w)/dw 就是函数 J(w)对 w 求导（derivative），在代码中我们会使用 dw 表示这个结果。

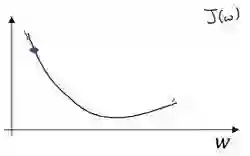
对于导数更加形象化的理解就是斜率（slope），如图该点的导数就是这个点相切于 J(w)的小三角形的高除宽。假设我们以如图点为初始化点，该点处的斜率的符号是正的，即dJ(w)/dw>0，所以接下来会向左走一步。

整个梯度下降法的迭代过程就是不断地向左走，直至逼近最小值点。

假设我们以如图点为初始化点，该点处的斜率的符号是负的，即dJ(w)/dw<0，所以接下来会向右走一步。

整个梯度下降法的迭代过程就是不断地向右走，即朝着最小值点方向走。

梯度下降法的细节化说明（两个参数）

逻辑回归的代价函数（成本函数）J(w,b)是含有两个参数的。

∂表示求偏导符号，可以读作 round；∂J(w,b)/ ∂w 就是函数 J(w,b)对 w 求偏导，在代码中我们会使用 dw 表示这个结果；∂J(w,b)/ ∂b 就是函数 J(w,b)对 b 求偏导，在代码中我们会使用 db 表示这个结果；小写字母 d 用在求导数（derivative），即函数只有一个参数偏导数符号∂用在求偏导（partial derivative），即函数含有两个以上的参数。

2.5 导数（Derivatives ）

这个视频我主要是想帮你获得对微积分和导数直观的理解。或许你认为自从大学毕业以后再也没有接触微积分。这取决于你什么时候毕业，也许有一段时间了，如果你顾虑这点，请不要担心。为了高效应用神经网络和深度学习，你并不需要非常深入理解微积分。因此如果你观看这个视频或者以后的视频时心想:“哇哦，这些知识、这些运算对我来说很复杂。”我给你的建议是：坚持学习视频，最好下课后做作业，成功的完成编程作业，然后你就可以使用深度学习了。在第四周之后的学习中，你会看到定义的很多种类的函数，通过微积分他们能够帮助你把所有的知识结合起来，其中有的叫做前向函数和反向函数，因此你不需要了解所有你使用的那些微积分中的函数。所以你不用担心他们，除此之外在对深度学习的尝试中，这周我们要进一步深入了解微积分的细节。所有你只需要直观地认识微积分，用来构建和成功的应用这些算法。最后，如果你是精通微积分的那一小部分人群，你对微积分非常熟悉，你可以跳过这部分视频。其他同学让我们开始深入学习导数。

我在这里画了一个函数 f(a)=3a，它是一条直线。下面我们来简单理解下导数。让我们看看函数中几个点，假定 a=2，那么 f(a) 是 a 的 3 倍等于 6，也就是说如果 a=2，那么函数 f(a)=6 。假定稍微改变一点点 a 的值，只增加一点，变为 2.001，这时 a 将向右做微小的移动。0.001 的差别实在是太小了，不能在图中显示出来，我们把它右移一点，现在 f(a) 等于 a 的 3 倍是 6.003，画在图里，比例不太符合。请看绿色高亮部分的这个小三角形，如果向右移动 0.001，那么 f(a) 增加 0.003， f 的值增加 3 倍于右移的 a ，因此我们说函数 f(a) 在 a=2，是这个导数的斜率，或者说，当 a=2 时，斜率是 3。导数这个概念意味着斜率，导数听起来是一个很可怕、很令人惊恐的词，但是斜率以一种很友好的方式来描述导数这个概念。所以提到导数，我们把它当作函数的斜率就好了。更正式的斜率定义为在这个绿色的小三角形中，高除以宽。即斜率等于 0.003 除以 0.001，等于 3。或者说导数等于3，这表示当你将 a 右移 0.001，f(a) 的值增加 3 倍水平方向的量。

现在让我们从不同的角度理解这个函数。假设 a=5 ，此时 f(a)=3*a =15 。我再一次把 a 右移一个很小的幅度，增加到 5.001，f(a) 等于 15.003。再一次当 a 向右移 0.001，f(a) 增加 3 倍。所以在 a 等于 5 时，斜率是 3。所以我们将函数 f 等于 3 的斜率表示为，这就是表示，当微小改变变量 a 的值，等于 3。一个等价的导数表达式可以这样写，不管你是否将 f(a) 放在上面或者放在右边都没有关系。这些等式表示，如果将a 右移一点，那么 f(a) 增加 3 倍。在这个视频中，我讲解导数讨论的情况是我们将 a 偏移0.001，如果你想知道导数的数学定义，导数是你右移很小的 a 值（不是 0.001，而是一个非常非常小的值）。通常导数的定义是你右移 a (可度量的值)一个无限小的值，f(a) 增加 3 倍（增加了一个非常非常小的值）。也就是这个三角形右边的高度。那就是导数的正式定义。但是为了直观的认识，我们将探讨右移 a=0.001 这个值，即使 0.001 并不是无穷小的可测数据。导数的一个特性是：这个函数任何地方的斜率总是等于 3，不管 a=2 或 a=5，这个函数的斜率总等于 3，也就是说不管 a 的值如何变化，如果你增加 0.001， f(a) 的值就增加3 倍。这个函数在所有地方的斜率都相等。一种证明方式是无论你将小三角形画在哪里，它的高除以宽总是 3。

我希望带给你一种感觉：什么是斜率？什么是导函数？对于一条直线，在例子中函数的斜率，在任何地方都是 3。在下一个视频让我们看一个更复杂的例子，这个例子中函数在不同点的斜率是可变的。

---

         欢迎关注公众号学习交流~