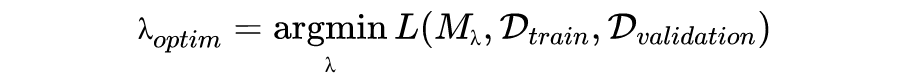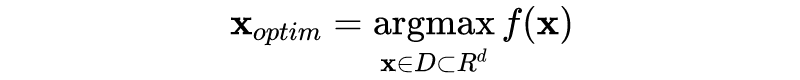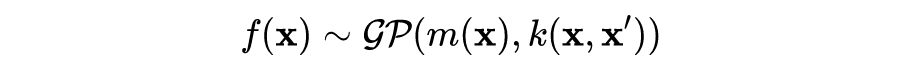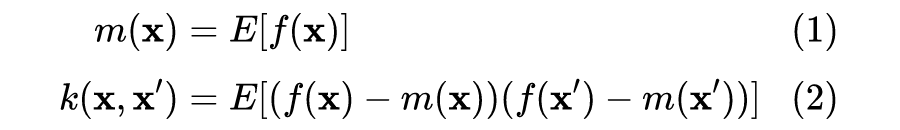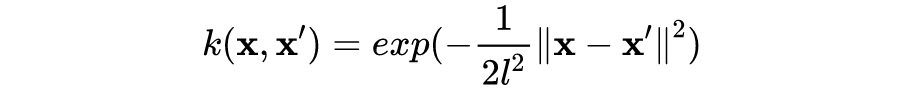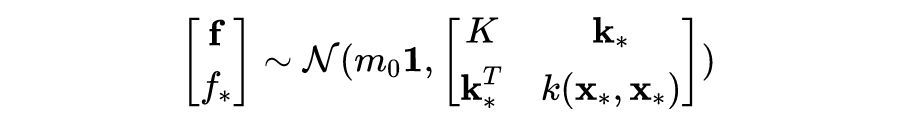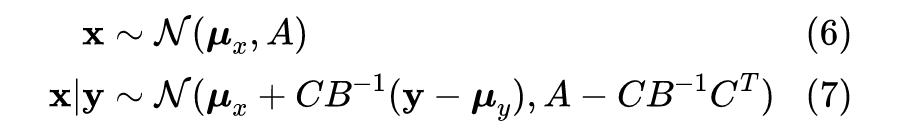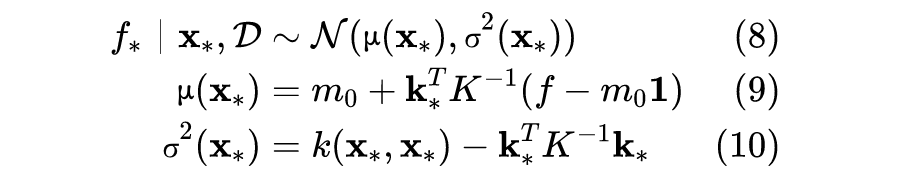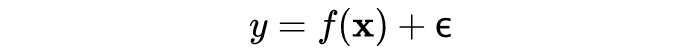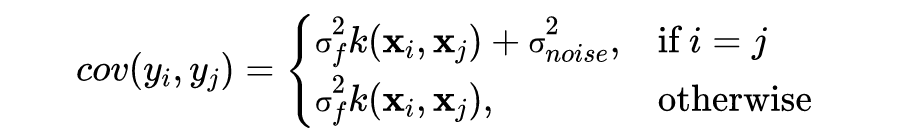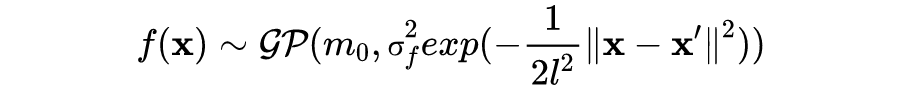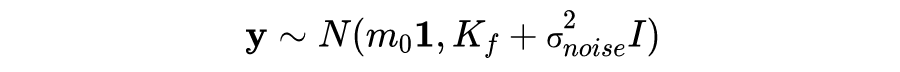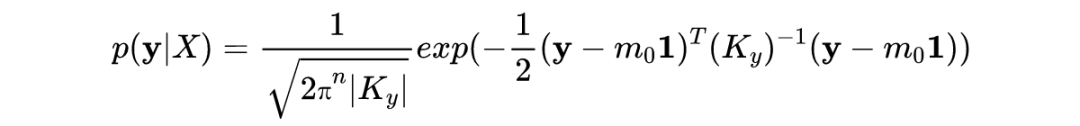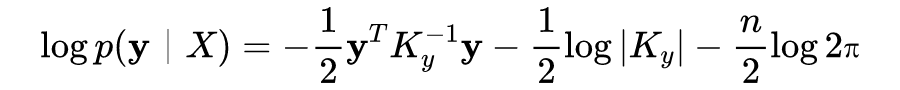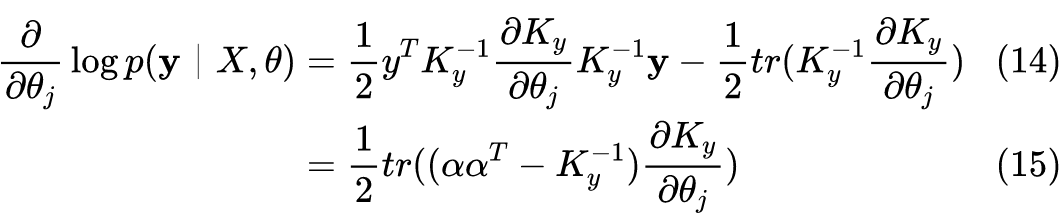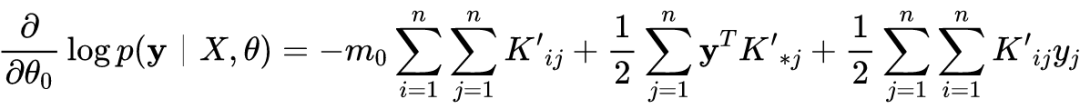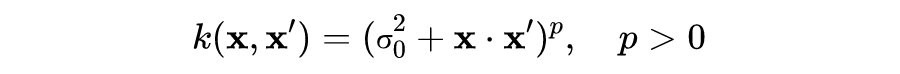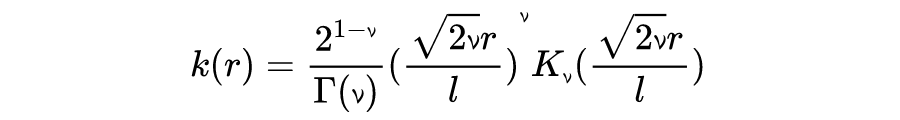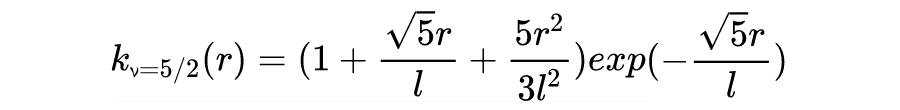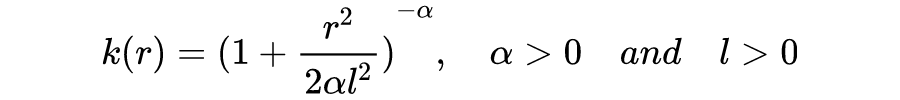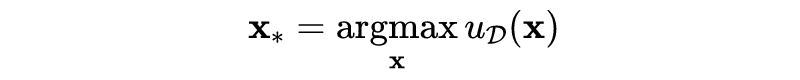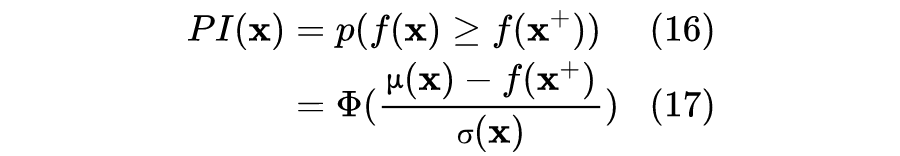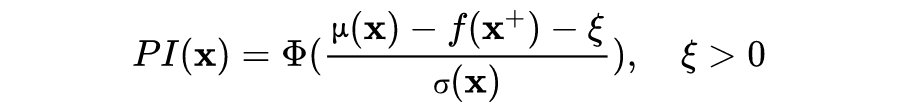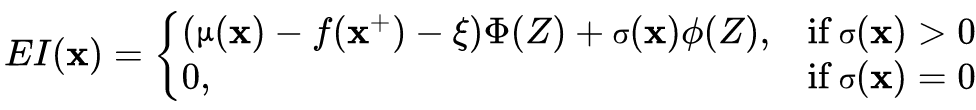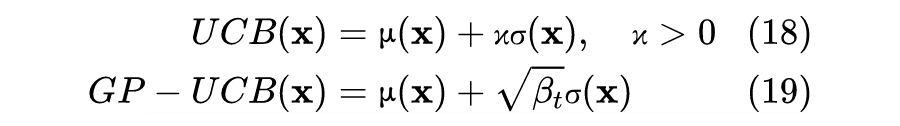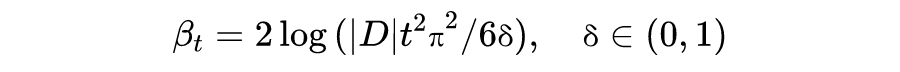一文详解超参数调优方法

©PaperWeekly 原创 · 作者｜王东伟

单位｜Cubiz

研究方向｜深度学习

本文介绍超参数（hyperparameter）的调优方法。

神经网络模型的参数可以分为两类：

1. 模型参数，在训练中通过梯度下降算法更新；
2. 超参数，在训练中一般是固定数值或者以预设规则变化，比如批大小（batch size）、学习率（learning rate）、正则化项系数（weight decay）、核函数中的 gamma 等。

超参数调优的目标通常是最小化泛化误差（generalization error），也可以根据具体任务自定义其他优化目标。泛化误差是指预测未知样本得到的误差，通常由验证集得到，关于验证集可以参阅 Cross-validation (statistics). Wikipedia.。

调优的方法如网格搜索（grid search）、随机搜索（random search）、贝叶斯优化（bayesian optimization），是比较常用的算法，下文将作介绍。其他算法如基于梯度的优化（gradient-based optimization）、受启发于生物学的进化算法（evolution strategy）等，读者可以自行了解。

网格搜索 Grid search

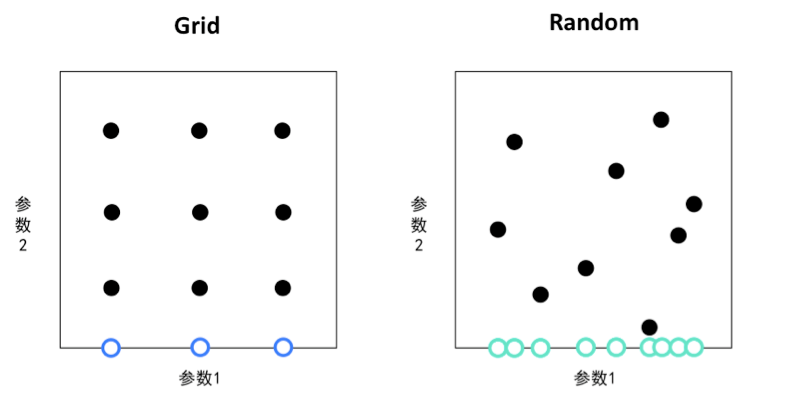
网格搜索就是遍历所有可能的超参数组合，找到能得到最佳性能（比如最小化泛化误差）的超参数组合，但是由于一次训练的计算代价很高，搜索区间通常只会限定于少量的离散数值，以下用一段伪代码说明：

def train(acf, wd, lr):
        优化目标函数得到模型M
        由验证集得到泛化误差e
        return e

learning_rate = [0.0001, 0.001, 0.01, 0.1]
weight_decay = [0.01, 0.1, 1]
activation = ['ReLU', 'GELU', 'Swish']

optimum = {'error': 1e10}

# grid search
for acf in activation:
        for wd in weight_decay:
                for lr in learning_rate:
                        error = train(acf, wd, lr)
                        if error < optimum['error']:
                                optimum['error'] = error
                                optimum['param'] = {
                                        'acf': acf,
                                        'wd': wd,
                                        'lr': lr
                                }

随机搜索 Random search

随机搜索在预先设定的定义域内随机选取超参数组合。实验证明随机搜索比网格搜索更高效，主要原因是随机搜索可以搜索连续数值并且可以设定更大的搜索空间，因此有几率得到更优的模型。另外，对于仅有少数超参数起决定性作用的情况，随机搜索对于重要参数的搜索效率更高。

如图 1，假设参数 2 几乎对优化目标没有影响，而参数 1 很重要，在同样进行 9 次采样的搜索中，网格搜索实际上仅对参数 1 采样了 3 次，而随机搜索为 9 次。关于随机搜索的实验可以查阅论文 Random Search for Hyper-Parameter Optimization. James Bergstra, Yoshua Bengio. 2012.。

▲ 图1

贝叶斯优化 Bayesian optimization

给定一组超参数，为了计算相应的模型泛化误差，我们需要进行一次完整的模型训练，对于大型的深度学习模型可能需要花上几个小时的时间。注意到网格搜索和随机搜索中，不同的超参数采样是相互独立的，一个直接的想法是，能否充分利用已采样数据来决定下一次采样，以提高搜索效率（或者说减少采样次数）。

早在 1960 年，就有科学家 Danie G. Krige 用类似的方法用于金矿分布的估计，他用已开采的少数矿点对金矿分布进行建模，后来这类方法被称为 Kriging 或高斯过程回归（Gaussian process regression, GPR）。

本文将介绍基于高斯过程的贝叶斯优化，其他类型的贝叶斯优化算法将在文末作简要总结。此外，本文关于 GPR 的数学原理部分参考了 MIT 出版的 Gaussian Processes for Machine Learning. C. E. Rasmussen, C. K. I. Williams. 2006（下文简称GPML），读者可自行查阅。

3.1 算法简介

超参数优化可以视为求解泛化误差的极值点：

其中， 为训练集和验证集， 为带参数模型。

以下为了方便讨论并且与相关领域的论文保持一致，我们用 表示待优化的目标函数，并且假设我们的目标是求极大值：

贝叶斯优化的算法如下：

可以看到，贝叶斯优化每次迭代都充分利用历史采样信息得到新的采样点，采样函数 的目标是让新的采样点尽可能接近极值点，因此，贝叶斯优化有可能以更少的采样得到优化结果。

GP 模型可以理解为函数，不过其对于未知输入 的预测不是一个确定的数值，而是一个概率分布。对于给定的 ， 将得到正态分布的均值 和方差 ，也就是说， 将给出目标函数值 的概率分布，即 。

图 2 为 3 次采样后（也就是已知样本数量为 3）GP 模型拟合结果的可视化，样本输入为 1 维，其中黑色曲线为均值 ，蓝色区域为一个标准差的置信区间。

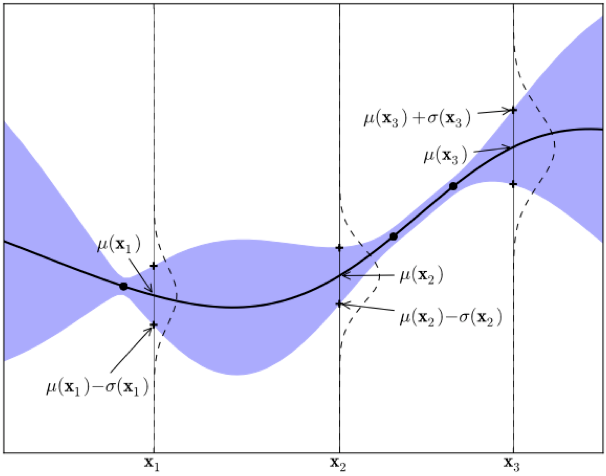
▲ 图2，源：https://arxiv.org/abs/1012.2599

3.2 高斯过程

具体地，我们假设随机变量集合 为高斯过程，其由均值函数（mean function） 和协方差函数（covariance function） 定义：

其中：

通常我们假设均值函数为常数 。协方差函数的常见选择是平方指数（squared exponential，SE）函数，也叫高斯核：

容易发现，上述协方差函数描述了不同输入之间的距离，或者说相似性（similarity）。对于回归或者分类问题，一个合理的假设是，距离较近的输入 x 有相近的目标函数值（或者类别标签）y，比如在分类问题中，距离测试样本更近的训练样本将提供更多关于测试样本类别的信息。可以说，协方差函数“编码”了我们对目标函数的假设。

现在，假如我们有了一些观测数据 ，其中， 。令 ，根据高斯过程的性质， 和测试样本 服从联合高斯分布：

其中， 是元素值全为 1 的向量。 为格莱姆矩阵（Gram matrix）。

可以证明，对于服从联合高斯分布的随机向量 和 ，

有：

因此：

到这里，我们几乎完成了贝叶斯优化的 GP 模型拟合部分，接下来，还需要作一些调整。

3.3 观测值噪声

在实际的项目中，目标函数的观测值 通常带有随机噪声 ，即：

一般来说，我们可以假设噪声服从零均值高斯分布， ，并进一步假设不同观测样本的噪声独立同分布，因此对于带噪声的观测样本，其关于协方差函数的先验变成：

注意到我们增加了参数 ，表示目标函数的方差。

容易得到：

其中， 为单位矩阵，， ， 。

进一步得到：

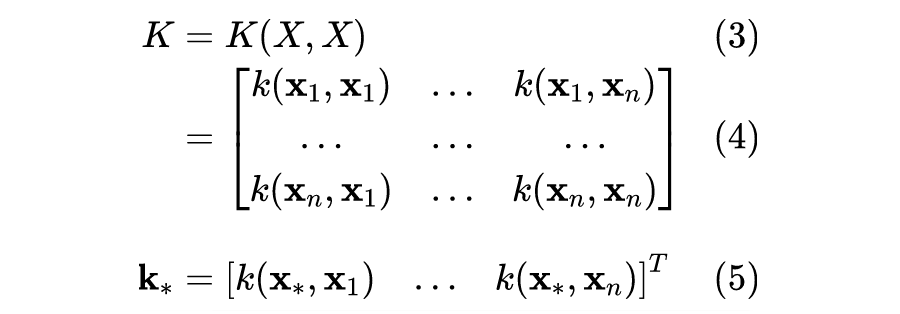
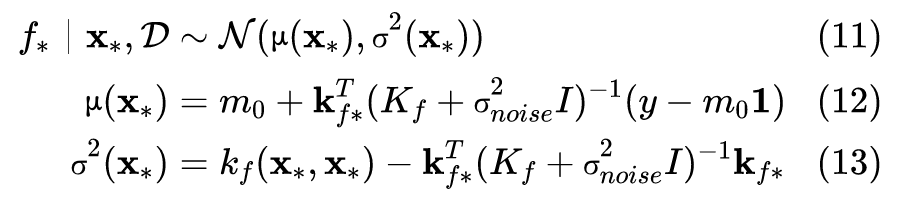
3.4 GP模型的超参数

注意到，以上关于 概率分布的预测包含参数 ，我们称之为 GP 模型的超参数。需要指出的是，GP 模型是一种非参数（non-parametric）模型（这里的参数应该类比神经网络的权重和偏置），超参数是独立于模型拟合过程的自由参数。

回顾对于目标函数 的先验假设：

在无观测数据的情况下，符合该先验的函数构成一个函数集合。通过多元高斯分布采样（参阅[GPML, Appendix A, A.2]），我们可以得到 时， 关于 的一种采样结果（考虑到可视化的便利性， 为 1 维），并由插值方法得到函数曲线，如图 3：

▲图3

可以看到 l 与采样函数随着 变化的剧烈程度有关。关于其他超参数如何影响 GP 模型的探讨，请参阅 [GPML, Chapter 5]。

通过最大化边缘似然（marginal likelihood） ，可以得到 GP 模型超参数的最优值，通常称该方法为极大似然估计（maximum likelihood estimate, MLE）。 为观测数据， 之所以被称为边缘似然来源于其积分表达式：

我们可以通过高斯分布的性质得到上述积分结果，不过我们已经从上文得到观测值服从高斯分布：

即：

取 log 得到：

其中， 为矩阵行列式， 。

可以看到 仅仅取决于均值常数 ，矩阵 的参数 和随机噪声 。我们把 统一表示为 ，其中  表示  。由相关的矩阵求导公式（参阅 [GPML, Appendix A, A.3]），容易求得 关于 的梯度：

其中， ， 。

此外，容易得到：

其中， ， 表示第 列的列向量。

接下来我们可以通过类似梯度上升的优化算法得到最优参数值。

其他 GP 模型的超参数优化方法，如极大后验估计（maximum a posteriori, MAP）和完全贝叶斯估计（fully Bayesian） 可参阅 A Tutorial on Bayesian Optimization. Peter I. Frazier. 2018.。

3.5 协方差函数

不同的协方差函数本质上隐含了对目标函数性质的不同假设。如果协方差函数是关于 的函数，那么它具有平移不变性，我们称它是平稳协方差函数（stationary covariance function），进一步，如果是关于 的函数，则该函数具有各向同性（isotropic）。可见，SE 函数是平稳的且各向同性的。

对于完全取决于内积 的函数，我们称之为内积协方差函数（dot product covariance function），它具有旋转不变形，但不是平稳的。一个内积协方差函数的例子：

平滑性（smoothness）。随机过程的平滑性由均方可微性（mean square differentiability）决定，比如，SE 函数对应的高斯过程是无限均方可微的。关于均方导数、均方可微的定义你可以自行了解。

以下介绍几个常见的平稳协方差函数形式。为了简洁，令 。

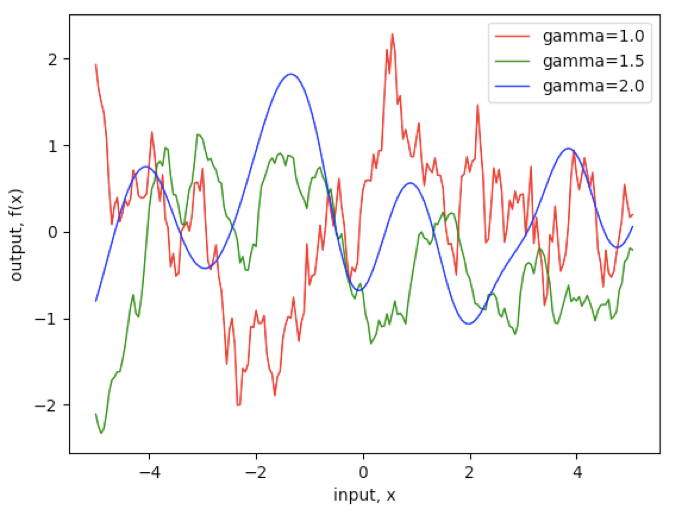
a. 伽马指数函数（γ-exponential covariance function）

除了 （相当于 SE）以外，它是非均方可微的。图4展示了 时的采样。

▲ 图4

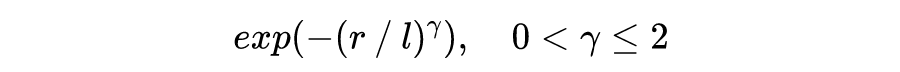
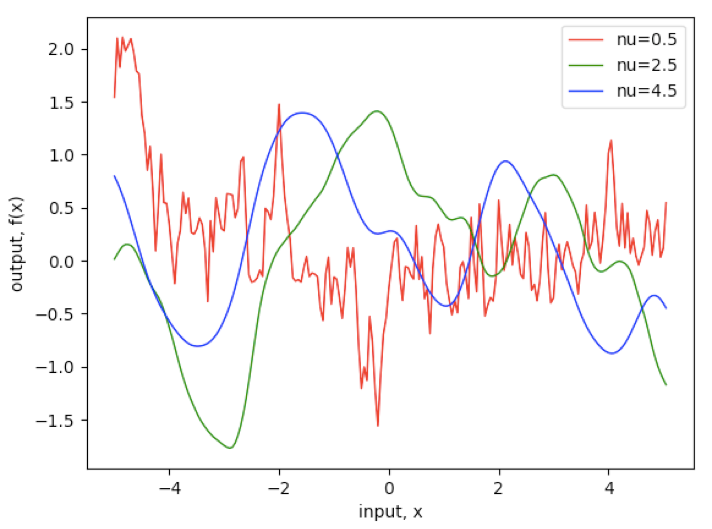
b. 马顿函数（The Matérn class of covariance functions）

其中， 为修正贝塞尔函数（modified Bessel function）， 为伽玛函数（gamma function）。图 5 展示了 时的采样。

▲ 图5

马顿函数在 均方不可微，而在 时为高阶均方可微。在一些论文中建议用 的马顿函数作为先验，它是二阶均方可微的，具有以下形式：

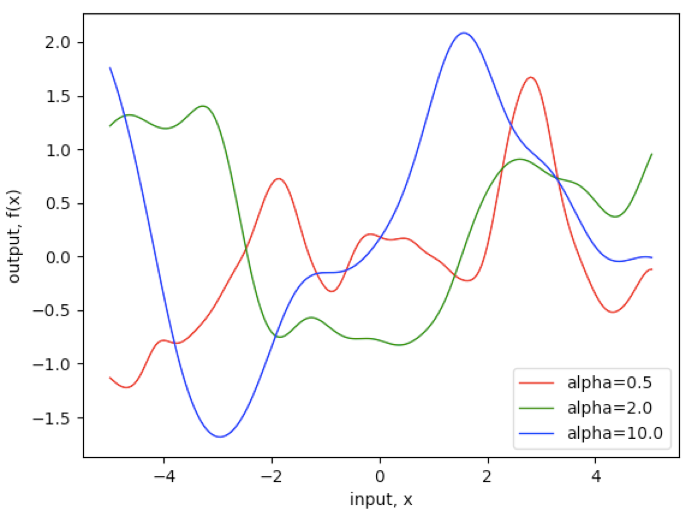
c. 二次有理函数（rational quadratic covariance function）

图6展示了 时的采样。

▲ 图6

以上协方差函数还有各向异性（anisotropic）的版本，可以通过替换 得到， 为对角矩阵。注意到各向同性的 SE 函数只有一个超参数 ，其各向异性版本则有 个超参数， 为 的维度。

3.6 采样函数

现在我们已经可以根据已有观测数据 得到一个用于预测新样本的 GP 模型 ，接下来我们考虑采样函数（acquisition function）的部分。采样函数的作用是让每一次采样都尽可能接近目标函数的极大值/极小值，以此提升极值点搜索效率。具体地，我们用 表示给定 GP 模型的采样函数，对于目标函数的下一次采样：

GP 模型给出的是目标函数的均值 和方差 ，一个直接的策略是，选择更大概率比当前观测数据的目标函数值更大的点（假设我们的目标是寻找极大值），令 为当前观测数据的最大值，可以得到采样函数：

其中， 是标准正态累积分布函数。

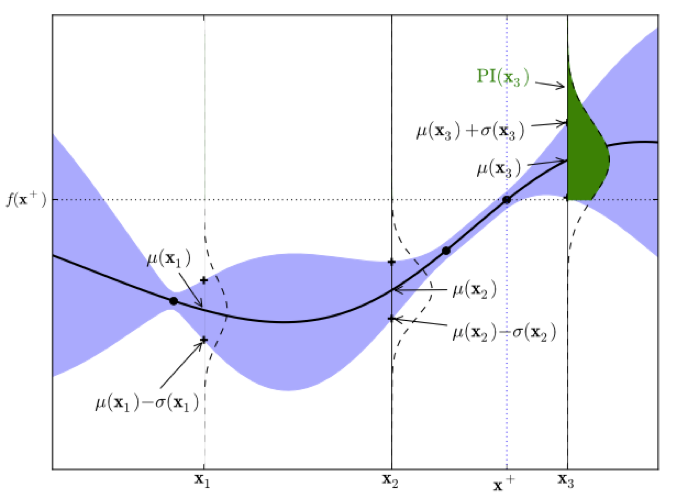
▲ 图7，源：https://arxiv.org/abs/1012.2599

通过分析可知，采样函数 倾向于以很高的概率略大于 的点，而不是以较低的概率大于 更多的点；前者更侧重以更高的把握取得提升（exploitation），后者侧重于探索高风险高收益的区域（exploration）。过于强调 exploitation 会导致优化过程陷入局部极值点，强调 exploration 则可能导致优化目标一直无法得到提升。因此采样函数的主要设计原则就是平衡 exploitation 和 exploration。以下列出几个常见的采样函数。

a. Probability of improvement (PI)

上述公式由 得到， 可以控制 exploration 的程度。论文作者建议对参数 建立一个规划表，在早期采样中设置高一些以强调 exploration，然后逐渐调低数值至零。

b. Expected improvement (EI)

其中， 是标准高斯分布的概率密度函数。EI 通过分析采样值提升的数学期望 得到， 同样用于平衡 exploitation-exploration，相关论文通过实验表明 可以在几乎所有实验案例中取得不错的表现。

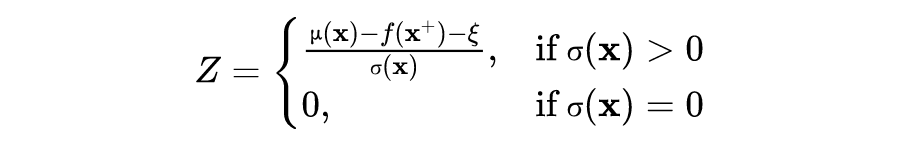
c. Upper confidence bound (UCB & GP-UCB)

UCB 由体现预期收益的部分 和体现风险的部分 构成，并通过参数 控制 exploration。

GP-UCB的 随采样进度 t 而变化，在原论文中实验采用的公式是：

实验中 。 表示对 的定义域 进行离散化取值得到的点数量，比如对于 1 维的情况， ，每隔 取一个 值，则 。论文还提到在实验中通过对 缩小 5 倍，可以获得性能提升 Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design. Niranjan Srinivas, Andreas Krause, Sham M. Kakade, Matthias Seeger. 2009.。

总结

协方差函数的选择。SE 函数是最常用的，但是因为基于 SE 的高斯过程是无限均方可微的，可见 SE 隐含了对目标函数平滑性的极端假设，因此有论文建议用 的马顿函数 Practical Bayesian Optimization of Machine Learning Algorithms. Jasper Snoek, Hugo Larochelle, Ryan P. Adams. 2012.。

均值函数。常数是比较常见的均值函数设置，如果目标函数可能有某种变化趋势，可以考虑采用参数化的均值函数，形如 A Tutorial on Bayesian Optimization. Peter I. Frazier. 2018.，或者基于概率模型的方法[GPML, Chapter 2]。

采样函数的选择。对于选择哪个采样函数目前没有明确的规则，有论文提出用组合采样函数的方法可以得到比单独使用更好的实验表现，参阅 Portfolio Allocation for Bayesian Optimization. Eric Brochu, Matthew W. Hoffman, Nando de Freitas. 2010.。其他采样函数，如 knowledge-gradient The Knowledge-Gradient Policy for Correlated Normal Beliefs. Peter Frazier, Warren Powell, Savas Dayanik. 2008.，entropy search (ES) Entropy Search for Information-Efficient Global Optimization. Philipp Hennig, Christian J. Schuler. 2012.，predictive entropy search (PES) Predictive Entropy Search for Efficient Global Optimization of Black-box Functions. José Miguel Hernández-Lobato, Matthew W. Hoffman, Zoubin Ghahramani. 2014.，结合 fully Bayesian 的GP EI MCMC Practical Bayesian Optimization of Machine Learning Algorithms. Jasper Snoek, Hugo Larochelle, Ryan P. Adams. 2012.，提升采样函数效率的 mixture cross-entropy algorithm Surrogating the surrogate: accelerating Gaussian-process-based global optimization with a mixture cross-entropy algorithm. R ́emi Bardenet, Bal ́azs K ́egl. 2010.。

其他贝叶斯优化算法。采用随机森林建模的 Sequential Model-based Algorithm Configuration (SMAC) Sequential Model-Based Optimization for General Algorithm Configuration. Frank Hutter, Holger H. Hoos, Kevin Leyton-Brown. 2011.，更适合高维度、离散化、超参数间有条件依赖的 Tree Parzen Estimator (TPE) Algorithms for Hyper-Parameter Optimization. James Bergstra, R ́emi Bardenet, Yoshua Bengio, Bal ́azs K ́egl. 2011.，以及提升 GP 模型计算效率的 SPGPs 和 SSGPs Taking the Human Out of the Loop: A Review of Bayesian Optimization. Bobak Shahriari, Kevin Swersky, Ziyu Wang, Ryan P. Adams, Nando de Freitas. 2016.。

最新的进展。2018年一篇关于贝叶斯优化的总结性论文 A Tutorial on Bayesian Optimization. Peter I. Frazier. 2018.，比较新的超参数优化算法 Hyperband Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. Lisha Li, Kevin Jamieson, Giulia DeSalvo, Afshin Rostamizadeh, Ameet Talwalkar. 2017.，结合了TPE和Hyperband的BOHB BOHB: Robust and Efficient Hyperparameter Optimization at Scale. Stefan Falkner, Aaron Klein, Frank Hutter. 2018.，Hyperband 和 BOHB 代码实现 HpBandSter. 2018.。

附录：部分算法的Python代码示例

a. 多元高斯分布采样。原理参阅[GPML, Appendix A, A.2]。

from matplotlib import pyplot as plt
import numpy as np

# SE协方差函数
kernel_se = np.vectorize(lambda x1, x2, l: np.exp(-(x1 - x2) ** 2 / (2 * l ** 2)))

def sample_se(x, l, mean=0):
        # x为numpy数组，e.g. x = np.arange(-5, 5, 0.05)
        x1, x2 = np.meshgrid(x, x)
        n = len(x)
        sigma = kernel_se(x1, x2, l) + np.identity(n) * 0.000000001
        L = np.linalg.cholesky(sigma)
        u = np.random.randn(n)
        y = mean + L @ u
        return y

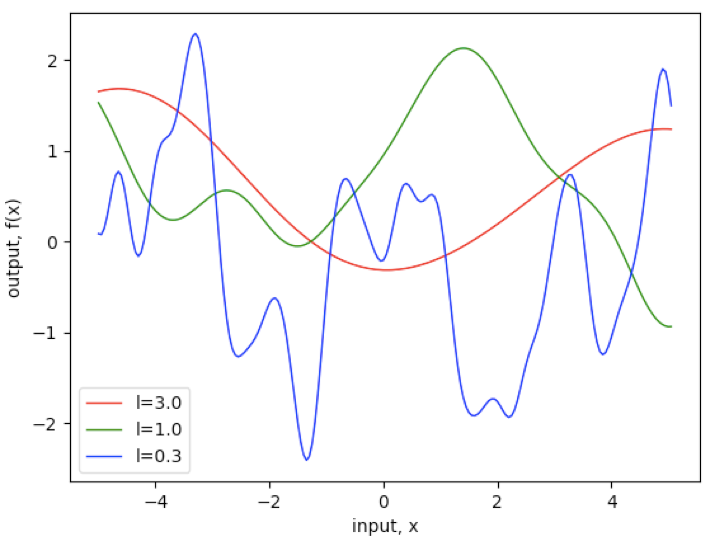
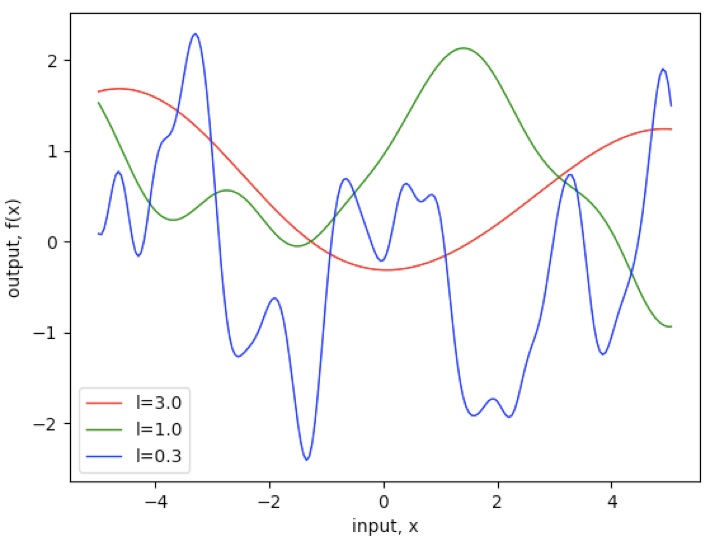
c = ['red', 'green', 'blue']
l = [3, 1, 0.3]

for i in range(len(l)):
        x = np.arange(-5, 5, 0.05)
        y = sample_se(x, l[i])
        plt.plot(x, y, c=c[i], linewidth=1, label='l=%.1f' % l[i])

plt.xlabel('input, x')
plt.ylabel('output, f(x)')
plt.legend(loc='best')
plt.show()

output：

b. 由观测数据集（X, Y）得到新样本的均值 和方差 。

from matplotlib import pyplot as plt
import numpy as np

# 目标函数                                                                                                                                                              
objective = np.vectorize(lambda x, std_n=0: 0.001775 * x**5 - 0.055 * x**4 + 0.582 * x**3 - 2.405 * x**2 + 3.152 * x + 4.678 + np.random.normal(0, std_n))

# 超参数                                                                                                                                                                
mean, l, std_f, std_n = 5, 1, 1, 0.0001

# SE协方差函数                                                                                                                                                          
kernel = lambda r_2, l: np.exp(-r_2 / (2 * l**2))

# 训练集，以一维输入为例                                                                                                                                                
X = np.arange(1.5, 10, 3.0)
X = X.reshape(X.size, 1)
Y = objective(X).flatten()

# 未知样本                                                                                                                                                              
Xs = np.arange(0, 10, 0.1)
Xs = Xs.reshape(Xs.size, 1)

n, d = X.shape
t = np.repeat(X.reshape(n, 1, d), n, axis=1) - X
r_2 = np.sum(t**2, axis=2)
Kf = std_f**2 * kernel(r_2, l)
Ky = Kf + std_n**2 * np.identity(n)
Ky_inv = np.linalg.inv(Ky)

m = Xs.shape[0]
t = np.repeat(Xs.reshape(m, 1, d), n, axis=1) - X
r_2 = np.sum(t**2, axis=2).T
kf = std_f**2 * kernel(r_2, l)
mu = mean + kf.T @ Ky_inv @ (Y - mean)
std = np.sqrt(std_f**2 - np.sum(kf.T @ Ky_inv * kf.T, axis=1))

x_test = Xs.flatten()
y_obj = objective(x_test).flatten()

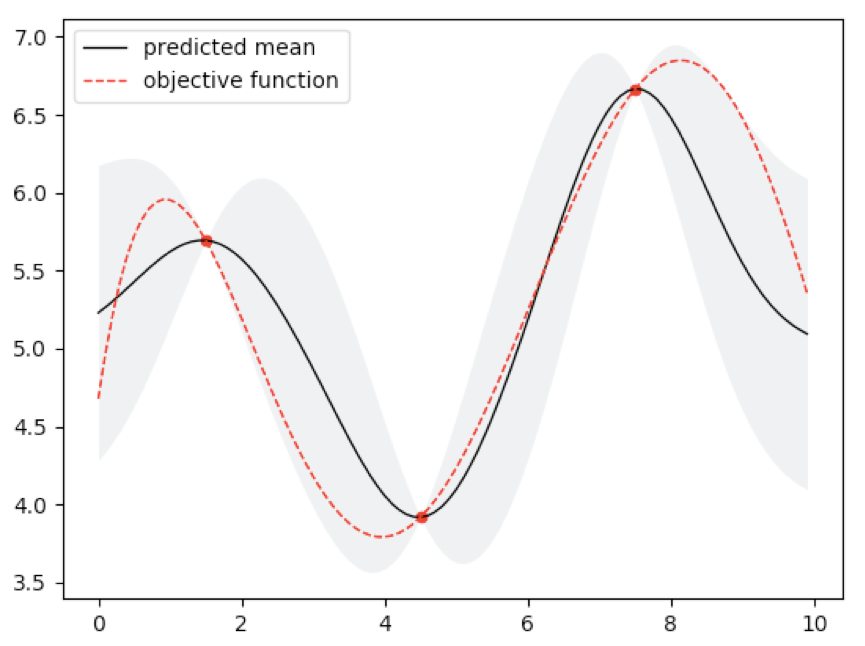
plt.plot(x_test, mu, c='black', lw=1, label='predicted mean')
plt.fill_between(x_test, mu + std, mu - std, alpha=0.2, color='#9FAEB2', lw=0)
plt.plot(x_test, y_obj, c='red', ls='--', lw=1, label='objective function')
plt.scatter(X.flatten(), Y, c='red', marker='o', s=20)
plt.legend(loc='best')
plt.show()

output：

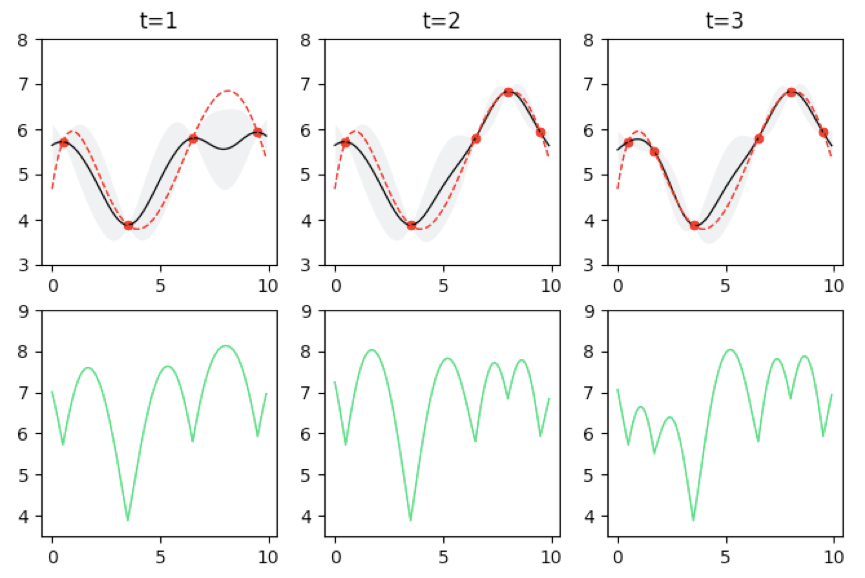
c. 贝叶斯优化示例。

from matplotlib import pyplot as plt
import numpy as np

# 目标函数                                                                                                                                                                  
objective = np.vectorize(lambda x, sigma_n=0: 0.001775 * x**5 - 0.055 * x**4 + 0.582 * x**3 - 2.405 * x**2 + 3.152 * x + 4.678 + np.random.normal(0, sigma_n))

# 采样函数 - GP-UCB                                                                                                                                                         
GPUCB = np.vectorize(lambda mu, sigma, t, ld, delta=0.1: mu + (1 * 2 * np.log(ld * t**2 * np.pi**2 / (6 * delta)))**0.5 * sigma)

# 超参数                                                                                                                                                                    
mean, l, sigma_f, sigma_n = 5, 1, 1, 0.0001

# 迭代次数                                                                                                                                                                  
max_iter = 3

# SE协方差函数                                                                                                                                                              
kernel = lambda r_2, l: np.exp(-r_2 / (2 * l**2))

# 初始训练样本，以一维输入为例                                                                                                                                              
X = np.arange(0.5, 10, 3.0)
X = X.reshape(X.size, 1)
Y = objective(X).flatten()

plt.figure(figsize=(8,5))

for i in range(max_iter):

        Xs = np.arange(0, 10, 0.1)
        Xs = Xs.reshape(Xs.size, 1)

        n, d = X.shape
        t = np.repeat(X.reshape(n, 1, d), n, axis=1) - X
        r_2 = np.sum(t**2, axis=2)
        Kf = sigma_f**2 * kernel(r_2, l)
        Ky = Kf + sigma_n**2 * np.identity(n)
        Ky_inv = np.linalg.inv(Ky)

        m = Xs.shape[0]
        t = np.repeat(Xs.reshape(m, 1, d), n, axis=1) - X
        r_2 = np.sum(t**2, axis=2).T
        kf = sigma_f**2 * kernel(r_2, l)

        mu = mean + kf.T @ Ky_inv @ (Y - mean)
        sigma = np.sqrt(sigma_f**2 - np.sum(kf.T @ Ky_inv * kf.T, axis=1))

        y_acf = GPUCB(mu, sigma, i + 1, n)
        sample_x = Xs[np.argmax(y_acf)]

        x_test = Xs.flatten()
        y_obj = objective(x_test).flatten()

        ax = plt.subplot(2, max_iter, i + 1)
        ax.set_title('t=%d' % (i + 1))
        plt.ylim(3, 8)
        plt.plot(x_test, mu, c='black', lw=1)
        plt.fill_between(x_test, mu + sigma, mu - sigma, alpha=0.2, color='#9FAEB2', lw=0)
        plt.plot(x_test, y_obj, c='red', ls='--', lw=1)
        plt.scatter(X, Y, c='red', marker='o', s=20)
        plt.subplot(2, max_iter, i + 1 + max_iter)
        plt.ylim(3.5, 9)
        plt.plot(x_test, y_acf, c='#18D766', lw=1)
        X = np.insert(X, 0, sample_x, axis=0)
        Y = np.insert(Y, 0, objective(sample_x))

plt.show()

output ：

参考文献

[1] Random Search for Hyper-Parameter Optimization. James Bergstra, Yoshua Bengio. 2012. 

[2] Gaussian Processes for Machine Learning. C. E. Rasmussen, C. K. I. Williams. 2006. 

[3] A Tutorial on Bayesian Optimization. Peter I. Frazier. 2018. 

[4] Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design. Niranjan Srinivas, Andreas Krause, Sham M. Kakade, Matthias Seeger. 2009. 

[5] Practical Bayesian Optimization of Machine Learning Algorithms. Jasper Snoek, Hugo Larochelle, Ryan P. Adams. 2012. 

[6] A Tutorial on Bayesian Optimization. Peter I. Frazier. 2018. 

[7] Portfolio Allocation for Bayesian Optimization. Eric Brochu, Matthew W. Hoffman, Nando de Freitas. 2010. 

[8] The Knowledge-Gradient Policy for Correlated Normal Beliefs. Peter Frazier, Warren Powell, Savas Dayanik. 2008. 

[9] Entropy Search for Information-Efficient Global Optimization. Philipp Hennig, Christian J. Schuler. 2012. 

[10] Predictive Entropy Search for Efficient Global Optimization of Black-box Functions. José Miguel Hernández-Lobato, Matthew W. Hoffman, Zoubin Ghahramani. 2014. 

[11] Practical Bayesian Optimization of Machine Learning Algorithms. Jasper Snoek, Hugo Larochelle, Ryan P. Adams. 2012. 

[12] Surrogating the surrogate: accelerating Gaussian-process-based global optimization with a mixture cross-entropy algorithm. R ́emi Bardenet, Bal ́azs K ́egl. 2010. 

[13] Sequential Model-Based Optimization for General Algorithm Configuration. Frank Hutter, Holger H. Hoos, Kevin Leyton-Brown. 2011. 

[14] Algorithms for Hyper-Parameter Optimization. James Bergstra, R ́emi Bardenet, Yoshua Bengio, Bal ́azs K ́egl. 2011. 

[15] Taking the Human Out of the Loop: A Review of Bayesian Optimization. Bobak Shahriari, Kevin Swersky, Ziyu Wang, Ryan P. Adams, Nando de Freitas. 2016. 

[16] A Tutorial on Bayesian Optimization. Peter I. Frazier. 2018. 

[17] Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. Lisha Li, Kevin Jamieson, Giulia DeSalvo, Afshin Rostamizadeh, Ameet Talwalkar. 2017. 

[18] BOHB: Robust and Efficient Hyperparameter Optimization at Scale. Stefan Falkner, Aaron Klein, Frank Hutter. 2018. 

[19] A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. Eric Brochu, Vlad M. Cora, Nando de Freitas. 2010. 

[20] Cross-validation (statistics). Wikipedia. 

[21] Markov chain Monte Carlo. Wikipedia. 

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。