介绍高维超参数调整 - 优化ML模型的最佳实践

本文为 AI 研习社编译的技术博客，原标题 ：

An introduction to high-dimensional hyper-parameter tuning

作者 | Thalles Silva

翻译 | Yulian       

校对 | 斯蒂芬·二狗子        审核 | Pita       整理 | 立鱼王

原文链接：

https://medium.freecodecamp.org/an-introduction-to-high-dimensional-hyper-parameter-tuning-df5c0106e5a4

注：本文的相关链接请访问文末【阅读原文】

如果你一直在努力调整机器学习模型(ML)性能,那么你读这篇文章算是找对了地方。

超参调整针对的问题是如何为一个学习算法找到最优参数的集合。

通常，选出这些值的过程是非常耗时的。

甚至最简单的算法像线性回归算法，找到超参的最优解集也是困难的。当涉及到深度学习算法，这件事会变得更艰难。

优化神经网络(NNs)时，一些需要调整的参数包括：

• 学习速率

• 动量

• 正则化

• dropout概率

• 批量标准化

在这篇短文中，我们谈论用于优化机器学习模型最优方法。当需要调整的参数超过两个或三个的时候，这些方法可以被使用。

  网格搜索问题

当我们只有少量的参数需要优化的时候，网格搜索通常是个好的选择。也就是说，对于两个甚至三个不同的参数，这也许就是正确的方式。

对每个超参数，首先需要定义待搜索的参数集合。

然后，该方法的思路尝试各个参数值之间的所有可能组合。

对于每次组合，我们训练和评估一个不同的模型。

最后，我们保留一个只有最小泛化误差的模型。

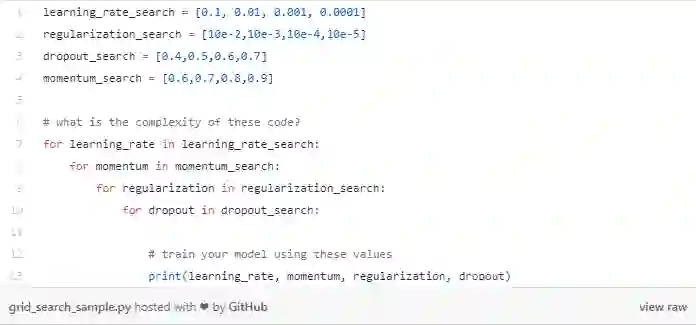
网络搜索的主要问题是一个指数时间算法。它的成本是随着参数的数量增加而呈指数增长。

换句话说，如果我们需要优化p个参数并且每个带有v个值，那它的执行时间是O(vᵖ) time。

同时，网格搜索在超参空间并不是如我们所想的有效。

在看一看上面的代码。使用这个实验设置，我们将要训练256个模型。注意如果我们决定多增加一个参数的寻优，实验的数字将会增至1024。

当然，目前的设置只会探索每个参数的四个不同的值。也就是说，我们训练256个模型只为探索学习率、正则化等四个值。

除此之外，网格搜索经常要求重复试验。比如将上面代码中learning_rate_search的值作为一个例子。

learning_rate_search = [0.1, 0.01, 0.001, 0.0001]

考虑一下第一次运行(256个模型试验)，我们找到了最好的模型的学习率是0.01。

在这种情况下，我们应该尝试通过在0.01左右的网格上“放大”来改进我们的搜索值，以便找到更好的值。

为了这个，我们可以设置一个新的网格搜索并重新定义学习率的搜索范围，比如：

learning_rate_search = [0.006, 0.008, 0.01, 0.04, 0.06]

但是如果我们得到的最好模型的学习率是0.0001怎么办？

由于这个值位于初始搜索范围的最边缘，因此我们应该改变搜索值，使用不同的集合重新搜索：

learning_rate_search = [0.0001, 0.00006, 0.00002]

并且尽可能的在找到一个好的候选值之后改进范围。

本文写这些细节只是为了强调超参搜索是多么耗时。

  一个更好的方法——随机搜索

如何随机选择我们的超参数候选值？尽管这种思路并不直观好理解，但某种程度上随机搜索比网格搜索更好。

一点点直觉

（读者）应注意到所提到的超参数中，某些超参数比其他参数更重要。

比如，学习率和动量因子比其他参数更值得调整。

但是，由于上述情况也存在例外，因此我们很难知道哪些参数在优化过程中起主要作用。实际上，我认为每个参数的重要性可能会因不同的模型体系结构和数据集而发生变化。

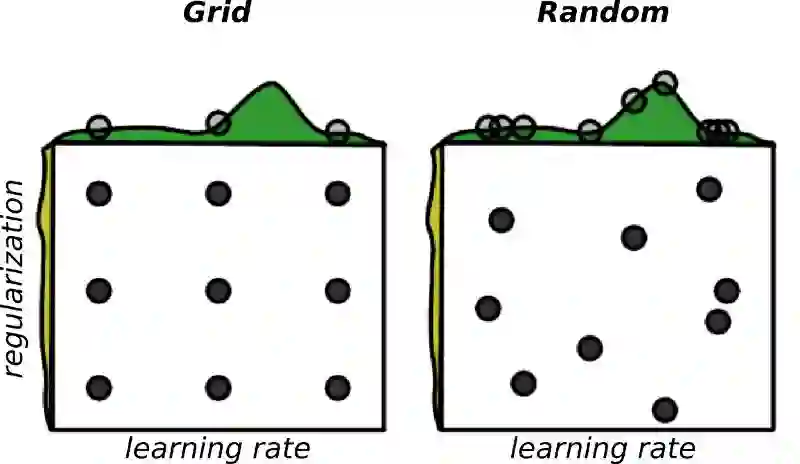
假设我们正在优化两个超参数 - 学习率和正则化系数。并且，我们考虑到只有学习率对问题是重要的。

在网格搜索的情况下，我们将进行九个不同的实验，但只尝试学习率的三个候选。

图片来源: Random Search for Hyper-Parameter Optimization, James Bergstra, Yoshua Bengio.

现在，看看如果我们对所有参数同时进行随机抽样候选值会发生什么。在这种情况下，我们实际上是正在为每个参数探索九个不同的值。

(举例)  如果您不相信，那么假设我们正在优化三个超参数。例如，学习率，正则化强度和动量。

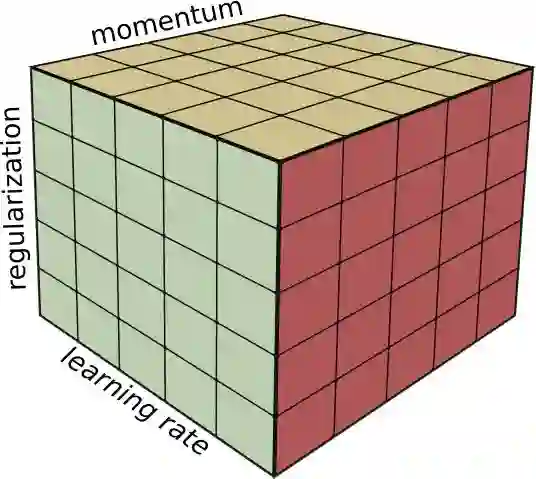
在3个超参数上使用网格搜索进行优化

使用网格搜索，我们需要运行125次训练，仅仅为了探索每个参数的五个不同值。

另一方面，使用随机搜索，我们将探索每个参数的125个不同的值。

怎么做

如果我们想试试优化学习率，比如值在0.1到0.0001的范围内，我们会：

请注意，我们是在对数函数下的均匀分布中采样。

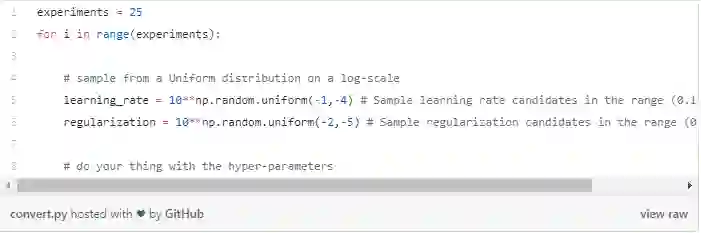
您可以将值-1和-4（学习率）视为指数，则真实区间为[10e-1,10e-4]。

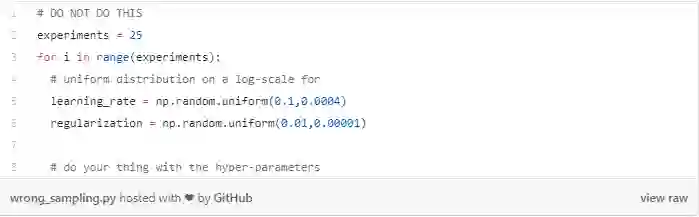
如果我们不使用对数方式，则会导致采样分布的不均匀。换句话说，您不应尝试如下采样：

在这种情况下，大多数值不会从“有效”区域采样。实际上，考虑到本例中的学习率样本，72％的值将落在区间[0.02,0.1]中。

此外，采样值中的88％将来自区间[0.01,0.1]。也就是说，只有12％的学习率候选值，即3个值，将从区间[0.0004,0.01]中采样。因此请不要那样做。

在下图中，我们从[0.1,0.0004]范围内抽取25个随机值。左上角的图显示了原始值。

在右上角，注意72％的采样值在[0.02,0.1]区间内。88％的值位于[0.01,0.1]范围内。

底部图显示了值的分布。只有12％的值是在[0.0004,0.01]区间内。要解决此问题，请从对数范围中的均匀分布中对值进行采样。

优化正则化参数时也会尝试取log

另外，请注意，与网格搜索一样，您需要考虑我们上面提到的两种情况。

如果最佳候选值非常接近边缘，那么您的范围可能会偏离，应该移动值范围并重新采样。此外，在选择好第一个候选值之后，可以尝试重新采样到更精细的值范围。

总之，这些是关键的要点。

• 如果要调整超过两个或三个超参数，则首选“随机搜索”。它比网格搜索更快/更容易实现和收敛。

• 使用适当的比例来选择您的值。可以试试对数空间中的均匀分布的样本取样。这将允许您对在参数范围内均匀分布的值进行采样。

• 无论是随机搜索还是网格搜索，都要注意您选择的候选值范围。确保正确设置参数的范围，并尽可能重新采样已得到更精确的结果。

想要继续查看该篇文章相关链接和参考文献？

点击底部【阅读原文】即可访问：

https://ai.yanxishe.com/page/TextTranslation/1623

AI求职百题斩 · 每日一题

每天进步一点点，长按扫码参与每日一题！

点击阅读原文，查看更多内容